磁力耦合器散热盘传热特性分析与结构参数改进

程刚，郭永存 王爽，陈健康

(安徽理工大学机械工程学院 矿山智能装备与技术安徽省重点实验室(安徽理工大学)，安徽淮南23200) (安徽理工大学机械工程学院，安徽 淮南 232001)

磁力耦合器散热盘传热特性分析与结构参数改进

程刚，郭永存 王爽，陈健康

(安徽理工大学机械工程学院 矿山智能装备与技术安徽省重点实验室(安徽理工大学)，安徽淮南23200) (安徽理工大学机械工程学院，安徽 淮南 232001)

以一台45kW双盘异步空冷式永磁涡流传动调速器为研究对象，采用仿真模拟的方法对该磁力耦合调速器散热盘热学特性进行了仿真计算与分析。结果表明，在设定条件下，铜转子模型温升梯度由铜转子中部沿径向外扩散，最高温度为533℃。选取散热结构中基板直径、厚度、翅片数量、高度与厚度为影响因素进行敏感度分析，在设定参数值内，基板厚度对铜转子最高温度影响敏感度较低，对模型总体质量影响敏感度较高；基板直径、翅片数量、翅片高度对铜转子最高温度影响敏感度较大，对模型总体质量影响敏感度较低；翅片厚度对铜转子最高温度几乎无影响，但对模型总体质量影响敏感度较高。基于敏感度分析结果，合理选取散热盘结构参数为基板直径⌀380mm、翅片数量28片和翅片高度24mm，仿真结果表明，改进后铜转子模型最高温度为48℃，相比之前下降103%，优化后模型质量为166kg，相比之前增长121%。

磁力；耦合器；散热；传热；优化

磁力耦合传动是目前兴起的一门传动技术，其发展历时并不久远，但发展迅速，近几年研究态势尤为迅猛。20世纪30年代，磁力传动技术就被提出。1946年，英国HMD无泄漏磁力泵公司将世界上第1台磁力传动泵推向市场并得到工业应用[1]；2008年，美国Magna Drive公司将永磁耦合传动技术引入中国；2016年，我国又将“永磁涡流柔性传动节能技术”列入《国家重点节能低碳技术推广目录》。磁力耦合传动装置是指在外力的作用下，利用传动部件中主、从动磁场产生的耦合力来实现力或转矩无接触传递的一种具备超矩特性与机械传动组合的新型传动装置，磁力耦合传动装置具有结构简易、体积较小、环境适应性强、节能减排、使用寿命长和安装方便等优点[1，2]，工业应用前景极为广阔。国内外学者对磁力耦合传动机理与结构设计做出了众多贡献[3～8]，随着理论的成熟与实践应用的普及，当前以磁力传动基础开发的产品也被越来越多的企业用户所接受，应用范围也逐步加大。

然而，在磁力耦合传动技术飞速发展的同时，在理论与实践中存在的一些技术性问题仍未得到恰当的解决，如散热问题[9，10]。磁力耦合传动系统在运行时，磁感应涡流损耗会产生大量的热，这会使系统中的结构部件出现温升现象，温升情况会影响导电材料的电导率与永磁材料磁性工作特性等，从而影响磁力耦合传动系统运行可靠性[11]，严重时会引起系统的故障。随着磁力耦合传动装置传递功率的增大，温升情况将更为严重，散热问题更加突出。以永磁涡流耦合调速器产品为例，当前主要采用空气和水冷却这2类方式来降低系统的温升影响，单机功率低于450kW一般以空气冷却方式为主，单机功率高于450kW一般以水冷却方式为主。水冷却方式将会额外增加设备成本，并且使整机结构体积增大，因而，尽可能改善以空气冷却方式的磁力耦合传动装置散热性能，最大程度地降低磁力耦合传动系统中零部件温度、合理设计其散热结构将具有重要的研究意义与工程应用价值。下面，笔者以一台45kW双盘异步式永磁涡流传动调速器(型号RDCOT310F，空气冷却式)为例，选取散热结构中基板直径、厚度、翅片数量、高度与厚度为影响因素，采用仿真模拟的方法对该磁力耦合调速器散热盘的热学特性进行了计算与分析，以期获得其因素影响特点与结构改进参数，为大功率的空气冷却式磁力耦合传动装置散热结构优化设计提供指导。

1 散热盘物理模型的构建

双盘异步式永磁涡流传动调速器中永磁转子(包括永磁体、铝制槽盘与端盖)与铜转子(包括铜盘、铁磁盘与散热盘)之间在工作时产生相对运动，永磁转子上所嵌入的永磁体切割铜盘产生涡流感应，进而通过磁感应耦合作用来传递转矩，永磁转子与铜转子之间存有气隙，通过气隙可以调节负载输出端的转速与转矩，实际结构如图1(a)所示。由于运行时存在涡流感应，因而铜转子上将会产生涡流热能，并以热传导、热对流和热辐射3类方式向外散热，铜转子上安装的散热盘(基板、翅片)将起到重要的散热作用，因而提高散热盘的散热性能至关重要。为方便研究，忽略类似于倒角、圆角、螺钉等细节，对散热盘的结构进行模型简化，散热盘为一零件体，研究时可分为基板与翅片2部分。以单侧盘为研究对象，简化铜转子与散热盘物理模型如图1(b)和(c)所示，铜转子相关零件的材料热物理属性如表1所示。原始结构参数如下：基板厚度a=5mm，基板直径d=340mm，翅片数量m=20片，翅片高度h=15mm，翅片厚度t=3mm，单侧铜转子模型初始质量M=14.8kg。

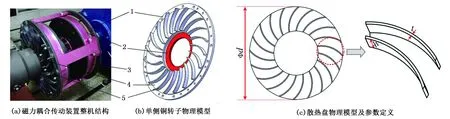
注：1-铁磁盘 ；2-铜盘；3-永磁转子；4-基板；5-翅片。图1 结构与物理模型

零件名称材料名称热传导系数/(W·(m·℃)-1)比热容/(J·(kg·℃)-1)密度/(kg·m-3)铜 盘铜3903908900铁磁盘Q235434407850散热盘Q235434407850

2 散热盘热学仿真计算与分析

2.1 热学分析与假设

在热学分析中，按照传热机理的不同，热量的传递方式分为热传导、热对流和热辐射3类。为使仿真计算更加贴近散热盘的传热工况，笔者以包含散热盘在内的单侧铜转子为整体研究对象，铜转子模型包含铜盘、铁磁盘和散热盘(含基板与翅片)3部分。铜转子的热量传递与散发过程为：铜盘为热源，它与铁磁盘相互接触，从而实现导热；铁磁盘与散热盘相互接触，实现导热。铜盘自身和铁磁盘及散热盘的所有外表面主要以对流与热辐射方式向环境散发热量。为简化求解模型，作以下假设：

1)铜盘上不考虑集肤效应，假定铜盘上的涡流损耗在铜盘内部分布均匀；

2)铜盘、铁磁盘和散热盘的材料为各向同性导热介质；

3)认为铜盘与铁磁盘、散热盘的连接为紧密接触，且不考虑接触表面所产生的热阻效应；

4)根据实际工况，永磁涡流耦合调速器工作环境中有轴流通风机强化散热，铜转子对流散热模式为强制热对流模式，其环境流体为标准大气压下的干燥空气；

5)忽略铜盘、铁磁盘和散热盘与空气之间的导热作用。

2.2 模型建立与计算

根据铜转子的运行环境与热学传递的特性，建立温度场求解的物理模型，对铜转子进行稳态热学分析。在热稳态中，系统内各点的温度仅与位置有关，不随时间变化而变化，热稳态分析的能量平衡方程为：

[K]{T}={Q}

式中，K为铜转子各部分热传导矩阵，包括导热系统、对流热系数、辐射率和形状系数；T为铜转子各部分节点温度阵列；Q为铜转子各部分节点热流量阵列。

给定求解域的边界条件及相关参数如下：

1)求解域为包括铜盘、铁磁盘和散热盘所在的三维模型区域；

2)在铜盘上施加体积热载荷，热载荷量为铜转子与永磁转子转差所引起的热功率，按一定转差运行情况，计算得单侧铜盘功率为500W；

3)根据通风机的安装与调节情况，设定散热盘、散热盘紧贴的铁磁盘端面均与空气之间的强制对流系数为30W/(m2·℃)；铜盘、其余铁磁盘面均与空气之间的强制对流系数为15W/(m2·℃)；环境温度设定为20℃；铜材料发射率为0.5，Q235发射率为0.6。

根据上述所建立的假设和边界条件，针对该永磁涡流调速器铜转子零部件的原始结构参数，基于Solidworks Simulation有限元分析环境对铜转子模型进行热学仿真计算。铜转子模型的有限元网格模型如图2所示，铜盘与铁磁盘、散热盘上的稳态温升分布情况如图3所示。热稳态时，所求解的区域铜转子模型温升分布由中部沿径向外扩散；铜转子的中铜盘上的最高温度为53.3℃，最低温度为51.2℃；铁磁盘上的最高温度为53℃，最低温度为48.6℃；散热盘上的最高温度处在基板上，为52.1℃，最低温度处在翅片上，为47.6℃。

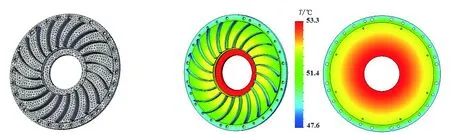
图2 模型有限元网格模型 图3 模型温升分布仿真结果

3 散热盘结构参数影响分析

基于对上述散热盘的仿真计算结果，为尽可能地改善散热盘散热情况，进一步认知铜转子上的最高温度与结构参数之间的影响关系，首先依次选取散热盘的基板厚度a、直径d、翅片数量m、高度h和厚度t为因素变量，采用仿真模拟方法对该磁力耦合调速器散热盘的热学特性进行计算与分析，研究因素变量对散热盘温升和质量变化的影响程度；其次，以仿真结果为基础，筛选散热盘结构参数变量并合理改进结构参数值，从而获得最佳的散热盘散热效果。

3.1 基板厚度a的影响

保持散热盘的其他结构物理参数不变，仅改变基板的厚度，仿真计算a∈[3mm,17mm],Δa=2mm模型的温升情况,不同基板厚度下所求模型的最高温度Tmax与总质量M变化如图4所示。

从图4可以看出，散热盘基板厚度从3～17mm逐渐增大时，铜转子的最高温度趋近下降状态，但下降幅度甚低，仅从53.4℃下降到52.3℃。原因在于，基板厚度的增加导致基板圆柱面的散热面积和热辐射面积增大，另一方面，基板厚度的增加会增大基板轴向的导热长度，这2个方面因素综合决定了铜转子的最高温度的升降趋势；同时，由于基板厚度的增加，铜转子的总质量趋进直线上升状态，增加幅度较大，从初始计算模型的13.7kg增大至21.5kg。因而，在该设定条件下，基板厚度对铜转子最高温度影响敏感度较低，以改变基板厚度来降低铜转子最高温度的方式不合适，且会增加模型的整体重量。

3.2 基板直径d的影响

保持散热盘的其他结构物理参数不变，仅改变基板的直径，仿真计算d∈[340mm,410mm],Δd=10mm模型的温升情况，不同基板直径下所求模型的最高温度Tmax与总质量M变化如图5所示。

从图5可以看出，基板直径在340～410mm逐渐增大时，铜转子的最高温度呈下降状态，下降幅度较高，从53.3℃下降到49.9℃。原因在于，基板直径的增加，基板的散热面积与热辐射面积增大，基板导热长度却无变化，因而温度具备下降条件；同时，由于基板直径的增加，铜转子的总质量趋进直线上升状态，从初始计算模型的14.8kg增大至16.5kg，整体增长幅度不大。因而，在该设定条件下，基板直径对铜转子最高温度有一定影响敏感度，以增加基板直径来降低铜转子最高温度的方式可行，且模型的整体重量增加较低。

图4 基板厚度与模型最高温度及总质量的关系 图5 基板直径与模型最高温度及总质量的关系

3.3 翅片数目m的影响

保持散热盘的其他结构物理参数不变，仅改变散热盘上的翅片的数目，仿真计算m∈[4,32],Δm=4模型的温升情况，不同翅片数目下所求模型的最高温度Tmax与总质量M变化如图6所示。

从图6中可以看出，翅片数量在4～32片逐渐增大时，铜转子的最高温度呈下降状态，从从56.7℃下降到51.2℃，整体温降比较显著。原因在于，翅片数量的增加，模型的散热面积与热辐射面积增大的效应比翅片导热长度增大的效应要强；同时，由于翅片数量的增加，铜转子的总质量成直线增长状态，但整体增幅较小，仅从初始计算模型的14.4kg增大至15.1kg。因而，在该设定条件下，翅片数量变化对铜转子最高温度影响敏感度较大，以改变翅片数量来降低铜转子最高温度的方式可行，且模型的整体重量增加较低，但由于所研究的散热盘上的翅片与基板成整体结构，因而在考虑改变翅片数量来降温的同时也需要兼顾加工费用。

3.4 翅片高度h的影响

保持散热盘的其他结构物理参数不变，仅改变翅片高度，仿真计算h∈[6mm,27mm],Δh=3mm模型的温升情况，不同翅片高度下所求模型的最高温度Tmax与总质量M变化如图7所示。

从图7可以看出，翅片高度在6～27mm逐渐增大时，铜转子的最高温度呈下降状态，从55.6℃下降到51℃，整体温降比较显著。原因在于，翅片高度的增加，模型的散热面积与热辐射面积增大的效应比翅片导热长度增大的效应要强；同时，由于翅片数量的增加，铜转子的总质量成直线增长状态，但整体增幅较小，仅从初始计算模型的14.4kg增大至15.5kg；整体增长幅度不大。因而，在该设定条件下，翅片高度变化对铜转子最高温度有一定影响敏感度，以增加翅片高度来降低铜转子最高温度的方式可行，且模型的整体重量增加较低。

图6 翅片数量与模型最高温度及总质量的关系 图7 翅片高度与模型最高温度及总质量的关系

3.5 翅片厚度t的影响

保持散热盘的其他结构物理参数不变，仅改变翅片厚度，仿真计算t∈[3mm,17mm],Δt=2mm时模型的温升情况，不同翅片厚度下所求模型的最高温度Tmax与总质量M变化如图8所示。

图8 翅片厚度与模型最高温度及总质量的关系

从图8可以看出，翅片厚度在3～17mm逐渐增大时，铜转子的最高温度处于稳定不变状态，基本恒定在55.6℃。原因在于翅片厚度的增加，翅片端面的散热面积和热辐射面积增大的效应与翅片厚度增加带来对流负影响的效应几近相同，因而总体温度情况处于持平；同时，由于翅片厚度的增加，铜转子的总质量趋于直线增长状态，整体质量有一定增幅，从初始模型的14.8kg增大至18kg。因而，在设定条件下，翅片厚度变化对铜转子最高温度无影响，以增加翅片厚度来降低铜转子最高温度的方式不可行，且会增加模型的整体重量。

4 散热盘结构参数改进及分析

从上述对散热盘的基板厚度、直径、翅片数量、高度和厚度对温升的影响结果可以看出，为降低铜转子上的温升并最大程度地降低其重量的增加量，可以选择基板直径、翅片数量与翅片高度3个参数来进行优化。同时，通过上述的研究分析可知，基板直径、翅片数量与翅片高度3个参数在研究范围内均与温升成增函数关系，且增加质量的程度较低，因而根据实际加工情况，合适地选择3类参数的最大数值。

考虑基板与铜盘的配合情况，取基板直径与铜盘直径相等，取∅380mm，并开设与铜盘上相同的通孔，保证连接板的安装；翅片与基板为一整体结构，翅片为铣加工工艺，考虑翅片数量对加工工艺与加工费用的影响，适当选取翅片数量为28片、翅片高度选取为24mm。针对上述参数进行模型修改并进行仿真计算，可得铜盘与铁磁盘、散热盘上的稳态温升分布情况，如图9所示。改进后铜转子模型的最高温度为48℃，相比改进前模型最高温度53.3℃下降10.3%；改进后模型质量为16.6kg，相比改进前模型质量14.8kg增长12.1%；铜转子的中铜盘上的最高温度为48℃，最低温度为45.6℃；铁磁盘上的最高温度为47.7℃，最低温度为42.7℃；散热盘上的最高温度处在基板上，为46.8℃，最低温度处在翅片上，为40.5℃。可见，合理改进散热盘结构参数可以有效改善铜转子模型温升情况。

5 结论

图9 改进后模型温升分布仿真结果

针对一台45kW双盘异步空冷式永磁涡流传动调速器中铜转子的热学特性进行了研究，采用计算机模拟仿真的方法获得了铜转子的散热盘基板厚度、直径、翅片数量、高度和厚度对模型温升结果的影响，基于计算结果，对模型的结构参数进行了合理改进，提高了模型的散热特性。

1)在所建立的假设和边界条件下，铜转子模型温升梯度由铜转子模型的中部沿径向外扩散；铜转子中铜盘上的最高温度为53.3℃，铁磁盘上的最高温度为53℃，散热盘上的最高温度处在基板上，为52.1℃。

2)在参数值设定范围内，基板厚度对铜转子最高温度影响敏感度较低，对模型总体质量影响敏感度较高；基板直径、翅片数量、翅片高度对铜转子最高温度影响敏感度较大，对模型总体质量影响敏感度较低；翅片厚度对铜转子最高温度几乎无影响，对模型总体质量影响敏感度较高。

3)基于敏感度分析结果与实际情况，筛选散热盘结构参数变量并合理改进结构参数值：基板直径∅380mm、翅片数量28片和翅片高度24mm。通过仿真计算可知，改进后铜转子模型温升情况得到明显改善，最高温度为48℃，相比改进前模型下降10.3%；改进后模型质量为16.6kg，相比改进前模型增长12.1%。

[1]赵克中.磁耦合传动装置理论与设计[M].北京：化学工业出版社,2009.

[2]牛耀宏.矿用永磁磁力耦合器设计理论及实验研究[D].北京：中国矿业大学(北京), 2014.

[3]杨超君,管春松,丁磊,等.盘式异步磁力联轴器传动特性[J].机械工程学报, 2014, 50(1):76～84.

[4]Wallace A, Jouanne A V. Industrial speed control: are PM couplings an alternative to VFDs[J]. IEEE Industry Applications Magazine, 2001, 7(5):57～63.

[5]Ravaud R, Lemarquand G,Lemarquand V, et al. Permanent Magnet Couplings: Field and Torque Three-Dimensional Expressions Based on the Coulombian Model[J]. IEEE Transactions on Magnetics, 2009, 45(4):1950～1958.

[6]Hogberg S, Jensen B B, Bendixen F B. Design and Demonstration of aTest-Rig for Static Performance-Studies of Permanent Magnet Couplings[J]. Magnetics IEEE Transactions on, 2013, 49(12):5664～5670.

[7]李延民，李申，邰志恒.软启动永磁涡流联轴器的设计与参数分析[J].中国机械工程, 2015(14): 1894～1899.

[8]时统宇, 王大志, 石松宁,等. 盘式永磁涡流驱动器的涡流软测量方法[J].电机与控制学报, 2016, 20(11):18～24.

[9]郑成龙.考虑声-固-热耦合影响的盘式可调速永磁联轴器降噪研究[D].济南：山东大学, 2015.

[10]焦兵锋.电磁液冷缓速器多场耦合分析与优化设计 [D].北京：北京工业大学, 2014.

[11]叶乐志，李德胜，王跃宗，等.选进汽车车缓速器理论与试验[M].北京：机械工业出版社, 2013.

[编辑] 洪云飞

2017-01-26

教育部高等学校博士学科点专项科研基金(20133415110003)；安徽省高校自然科学研究重点项目(KJ2017A083)。

程刚(1986-)，男，硕士，讲师，现主要从事磁力机械设计与光机电一体化方面的研究工作，gang740@126.com。

TH133

A

1673⁃1409(2017)09⁃0022⁃06

[引著格式]程刚，郭永存,王爽，等.磁力耦合器散热盘传热特性分析与结构参数改进[J].长江大学学报(自科版)，2017,14(9)：22～27.