几种模块化多输出电力电子变压器拓扑的不平衡负载补偿能力比较

欧阳少迪， 刘进军

(西安交通大学电气工程学院， 陕西 西安 710049)

几种模块化多输出电力电子变压器拓扑的不平衡负载补偿能力比较

欧阳少迪， 刘进军

(西安交通大学电气工程学院， 陕西 西安 710049)

电力电子变压器除了能实现传统变压器的变压/隔离功能之外，还需要根据用户需求提供一些额外功能，其中之一是多输出功能，即给多个独立的交/直流负载供电。因为负载不平衡工况会对电力电子变压器的运行提出挑战，因此当设计一台具有多输出功能的电力电子变压器时，需要确定合适的拓扑与控制策略。本文对三种电力电子变压器拓扑的补偿不平衡负载的能力进行了比较，包括：独立相连接拓扑，交叉相连接拓扑与自平衡拓扑。独立相连接拓扑通过在输入级中注入零序分量来实现不平衡负载的补偿；交叉相连接拓扑通过输入级调制度以及无功分量注入实现不平衡负载的补偿；自平衡拓扑通过拓扑自身的连接方法以及多端口高频变压器实现不平衡负载的补偿，拓扑较为复杂。本文分析了上述三种电力电子变压器拓扑的原理以及控制策略，并在SIMULINK中验证了这几种拓扑补偿不平衡负载的功能。

电力电子变压器； 多输出； 不平衡负载； 拓扑

1 引言

电力电子变压器(Power Electronic Transformer, PET), 又称固态变压器(Solid State Transformer, SST), 是近年来发展迅速的一种新型电力电子装置。电力电子变压器除了能实现传统变压器的变压与隔离功能之外，还能实现许多额外的功能，包括电压/电流闭环控制、无功/谐波补偿、提供直流端口、多输出等[1,2]。目前电力电子变压器已经应用在机车拖动中[3]，未来还将在新能源发电[4]、智能电网[5]等领域中得到应用。

根据拓扑中直流环节的配置情况，电力电子变压器的拓扑可以归为三大类：①单级拓扑，输入交流级与输出交流级均无直流环节，需要使用双向开关承受交流电压、电流。这种拓扑结构简单，可以达到最高的功率密度，但无法实现输入电流控制，功能最弱[6-8]；②双级拓扑，输入交流级与输出交流级中仅一级拥有直流环节，带直流环节级可以使用单向开关，另一级则必须使用双向开关。这种拓扑可以实现输入电流控制，但双向开关级的波形控制算法复杂，控制效果较差[9,10]；③三级拓扑，输入交流级与输出交流级均含直流环节，无需双向开关，可以实现输入电流控制，控制策略成熟，可以实现最多的功能；其缺点在于，相对于单级和双级拓扑，三级拓扑的效率最低，体积最大。目前，由于功能上的优势以及技术上的成熟性，三级结构拓扑是工程与研究中的主流拓扑。

电力电子变压器一般情况下需要连接不同等级的电压。其中低压交流级一般用于连接低压配电网或者低压电机，可以采用两电平变流器，较为常规；中/高压交流级一般用于连接中压以上的配电网，常规的两电平、三电平无法满足电压要求。目前中/高压级的拓扑方案主要有：基于碳化硅的三电平拓扑[11]、串联H桥以及模块化多电平变流器(Modular Multilevel Converter,MMC)[12]三种。从技术成熟度的角度，基于碳化硅的三电平拓扑目前只停留在实验室阶段；而综合考虑功能、造价与体积时，MMC方案并不经济，因此，目前串联H桥为电力电子变压器中/高压级的主流选择，电力电子变压器遂采用模块化结构。

在隔离级方面，电力电子变压器均选择双有源全桥(Dual Active Bridge, DAB)及其各种变种。

鉴于以上背景，三级拓扑、串联H桥与模块化结构成为了目前电力电子变压器的最典型特征，以FREEDOM电力电子变压器[5]为代表，图1为其拓扑图。中压输入级采用串联H桥；隔离级采用多个DAB变流器；DAB的低压侧直流输出合并为一个直流母线，可作为低压直流输出；在直流母线上接两电平逆变器，作为低压交流输出[13]。

图1 FREEDOM电力电子变压器Fig.1 Power electronic transformer by FREEDOM

因为存在公共的低压直流母线，FREEDOM拓扑可以给多个电压等级相同且不要求互相隔离的负载供电。而当多个负载电压等级不同，或者要求电气隔离时，就需要在低压直流母线上额外增加用于电压转换或者电气隔离的变流器,如图2所示。这种方案增加了系统的变流器总容量，因此，可以考虑不合并DAB的低压直流母线，直接通过不同的DAB给不同的负载供电，如图3所示。这就是本文要讨论的模块化多输出电力电子变压器。

图2 有公共直流母线的多输出电力电子变压器Fig.2 Multi-output PET with common DC bus

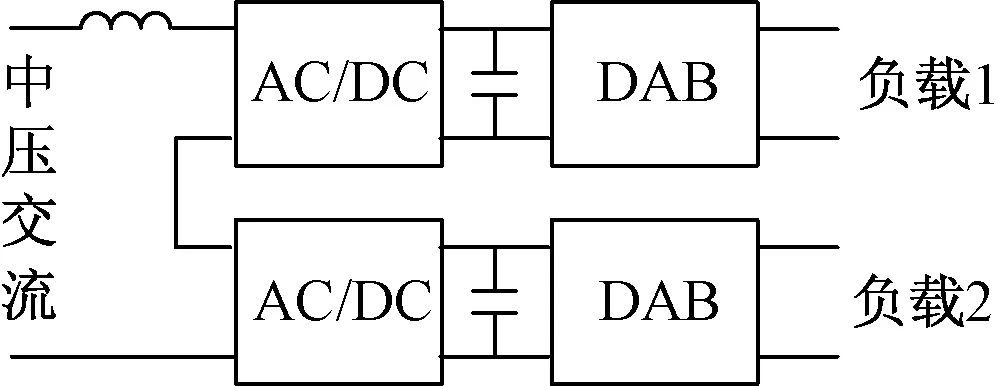
图3 不含公共直流母线的模块化多输出电力电子变压器Fig.3 Modular multi-output PET without common DC bus

因为负载不受控制，系统必然会面临负载功率不平衡的工况，这会导致中压输入级各个模块的功率不平衡，对电力电子变压器的运行和控制造成挑战。因此，需要对模块化多输出电力电子变压器的具体拓扑与控制策略进行研究，为未来可能的工程实施奠定一定的理论基础。

本文针对模块化多输出电力电子变压器，提出了几种拓扑/控制方案并进行了对比，包括独立相连接型拓扑、交叉相连接型拓扑与全范围自平衡拓扑。独立相连接型拓扑中，输入级三相的功率不均衡，但每相内的模块功率均衡，需通过零序分量注入来补偿三相不平衡功率。交叉相连接型拓扑中，输入级三相的功率均衡，但每相内的模块功率不均衡，需通过无功分量注入来避免模块过调制。全范围自平衡拓扑中，输入级三相的功率均衡，每相内模块的功率也均衡，不需任何补偿措施，但系统结构较复杂。

本文研究的多输出电力电子变压器的负载数量为三个，输出级为三相，每相带一个独立负载。

2 独立相连接电力电子变压器

独立相连接型(Separate Phase Connection, SPC)拓扑如图4所示。输入级采用星型(或三角形)连接的串联H桥变流器，隔离级采用DAB变流器，输出级采用H桥逆变器。输出级的三相分别对应输入级的三相。

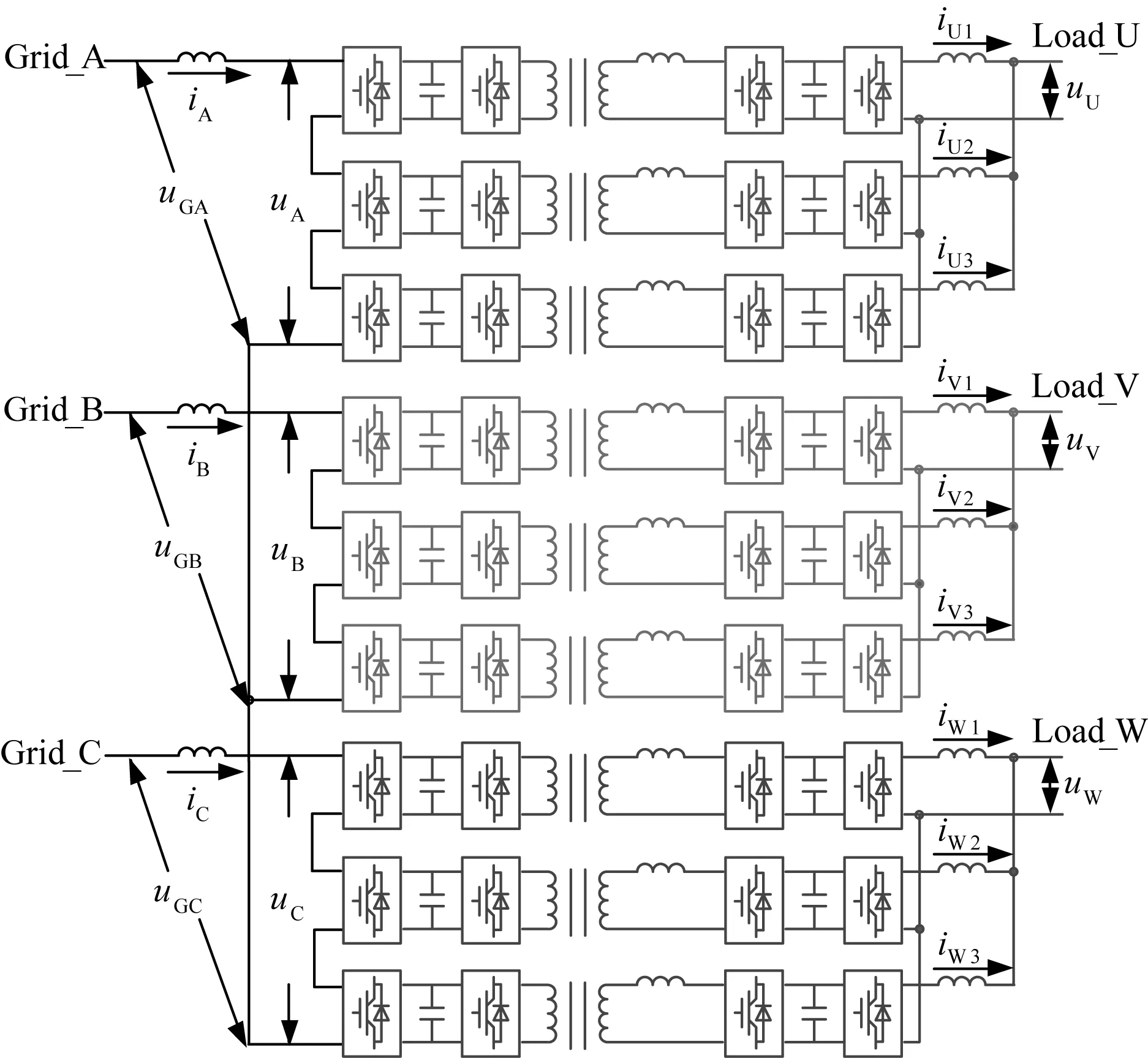
图4 独立相连接的电力电子变压器Fig.4 SPC PET

当输出级三相所带的三个负载不平衡时，输入级的三相功率也会不平衡。若不做任何补偿措施，则会在输入级电网中注入负序电流。

输入级星型连接的系统，可以通过在输入级变流器中注入合适的零序电压来完全补偿负序电流；输入级三角形连接的系统，可以通过在输入级变流器中注入合适的零序电流来完全补偿负序电流[14]。对输入级三角形连接的系统的分析见文献[15]，本文只分析星型连接的系统。

零序电压补偿量的计算如下。假设电网电流仅含正序，如式(1)所示，注入的零序电压如式(2)所示，则零序电压与正序电流作用得到的输入级三相的补偿功率如式(3)所示。当补偿功率已知，输入正序电流也已知时，可以通过求解式(3)来得到所需的零序电压，如式(4)所示。

(1)

(3)

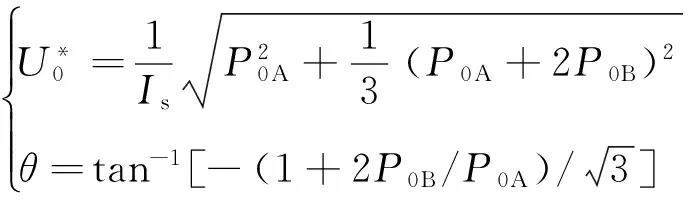
(4)

输入级的控制框图如图5所示。采用三层控制，第一层用来控制输入级的总输入功率并实现单位功率因数，如图5(a)所示；第二层用来控制三相桥臂中注入的零序电压，以补偿三相之间的不平衡功率，如图5(b)所示，零序电压指令计算采用式(1)～式(4)，图5(b)产生的零序电压指令作为5(a)中dq0/abc变换的0轴输入；第三层用来平衡每相内部各个模块的直流电压,把一相内每个模块的直流电压与该相所有模块的平均直流电压进行比较，通过PI产生各个模块的微调系数kXn(X=A,B,C；n=1,2,…,N，N为一相内的模块总数)，利用该微调系数调节每个模块的交流指令电压，如图5(c)所示。

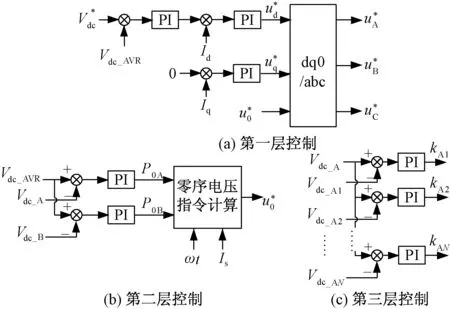
图5 输入级控制框图Fig.5 Control strategy of input stage

隔离级各个DAB变换器各自独立控制，在本文中不做讨论。各个DAB都采用单电压环控制，通过调节两个H桥之间的移相角以控制自身的输出侧直流电压，如图6所示。

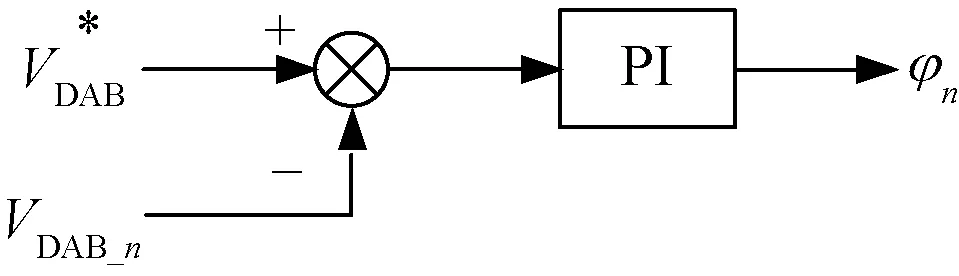
图6 隔离级DAB控制框图Fig.6 Control strategy of isolation stage

输出级采用常规的电压/电流双闭环控制，实现并联的各个模块的输出电流均分，如图7所示。

图7 输出级控制框图Fig.7 Control strategy of ouput stage

输入级桥臂电压与输入级电流向量(忽略了输入级滤波电感上的压降)如图8～图10所示。其中uAp、uBp、uCp为桥臂正序电压；u0为桥臂零序电压；uA、uB、uC为桥臂总电压；iA、iB、iC为桥臂电流。当输出级的三相功率平衡时，输入级的三相功率也平衡，此时输入级的电压/电流向量如图8所示，输入级电压均衡并与输入级桥臂电流同相位。当负载功率严重不均衡时，输入级电压/电流向量如图9、图10所示。在注入了零序电压后，输入级各相与电网电流无法再保持同相位，这使得输入级的桥臂电压大大高于额定值。可以看出，为了补偿0∶1∶1的负载功率，桥臂输出的交流电压需要提高到额定值的1.73倍；为了补偿最严重的1∶0∶0的负载功率，桥臂输出的交流电压需要提高到额定值的3倍。这意味着输入级星型连接的独立相连接拓扑需要很大的电压裕量来实现全范围不平衡负载补偿。

图8 额定平衡负载下的电压电流向量Fig.8 Vectors at rated balanced load

图9 0∶1∶1不平衡负载下的电压电流向量Fig.9 Vectors at 0∶1∶1 unbalanced load

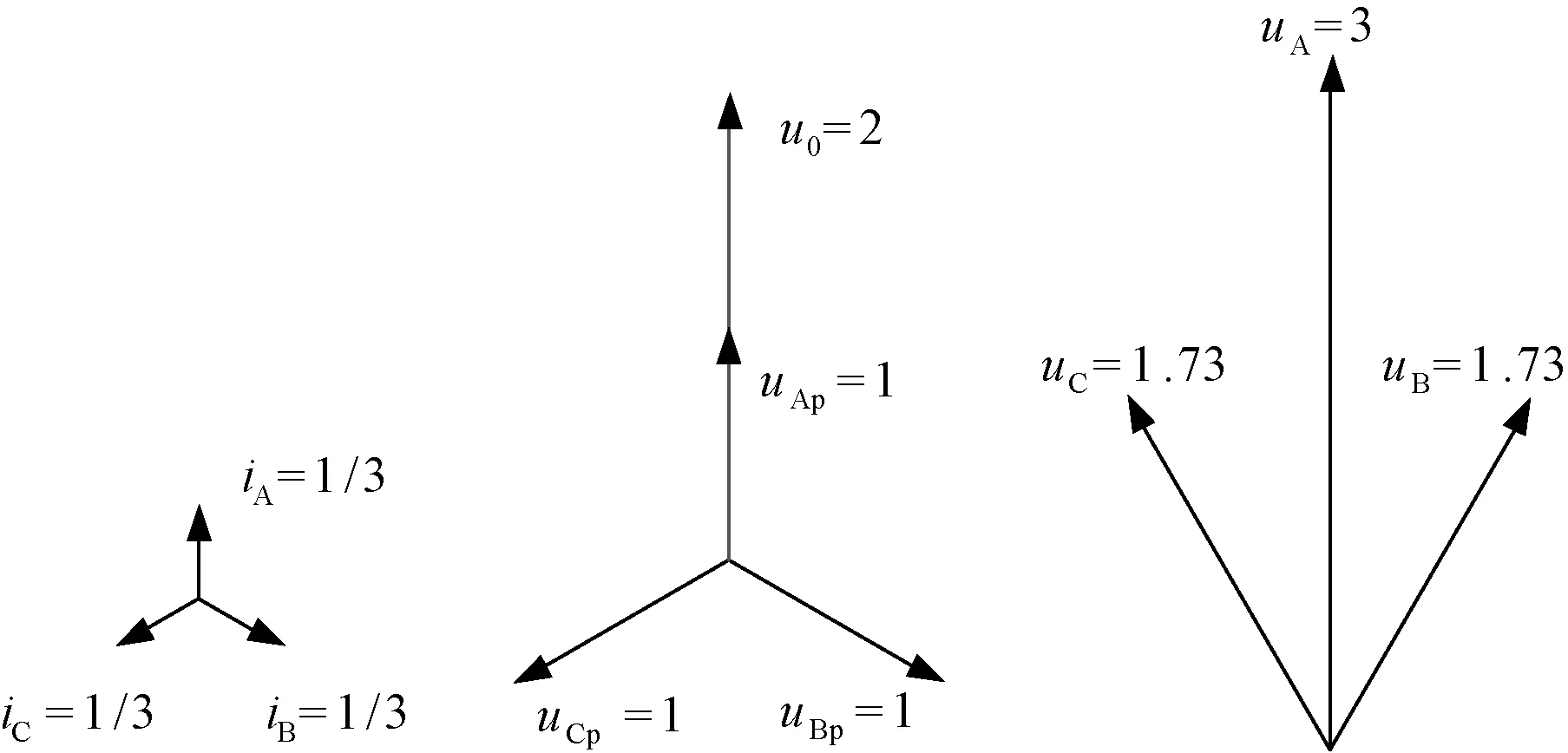
图10 1∶0∶0不平衡负载下的电压电流向量Fig.10 Vectors at 1∶0∶0 unbalanced load

对输入级三角形连接的独立相连接拓扑的分析见文献[15]。三角形连接的系统，可以通过在三角形内注入零序环流来实现不平衡的负载功率补偿，算法与式(1)～式(4)类似。为了实现全范围不平衡负载的补偿，三角形连接的输入级需要1.15倍的电流裕量[15]，这远远小于星型连接情况下的3倍电压裕量。

3 交叉相连接电力电子变压器

交叉相连接(Cross Phase Connection，CPC)的拓扑如图11所示。输入级采用星型连接的串联H桥变流器，隔离级采用多个DAB变流器，输出级采用常规H桥逆变器。这种交叉相连接的特点在于输出级每相内的各个模块分别连接到输入级的三相。

图11 交叉相连接的电力电子变压器Fig.11 CPC PET

在CPC拓扑中，输入级每相都能给输出级的所有相提供功率，输出级每相的功率都由输入级的三相平均提供。因此，无论输出级各相的功率如何不平衡，输入级三相的功率都是自动均衡的，输入级三相间无需进行功率补偿。

因为CPC拓扑对不平衡负载的补偿在单相串联H桥的子模块之间完成,因此CPC拓扑的输入级不需要三角形连接。值得强调的是，CPC拓扑的输入级仍然需要注入一定的零序电压，不过这个零序电压仅仅用于补偿输入级三相桥臂中的损耗差异，幅值非常小，可以忽略。与之对比，SPC拓扑中的零序电压用来补偿不平衡的负载功率，幅值相对较大。

CPC拓扑虽然实现了输入级三相功率的自动均衡，但带来了输入级各相内部子模块间的功率不均衡问题。在电流单位功率因数情况下，当负载严重不均衡时，会带来严重的模块交流电压不均衡问题，导致过调制。为了消除过调制，需要在系统中注入一定的无功分量。

3.1 电流单位功率因数情况

在电流单位功率因数情况下，负载不均衡功率只能通过调节各个模块的调制度来补偿。

电网电流、输入级A相桥臂电压、A相内各个子模块电压向量如图12所示。当负载均衡时，各个子模块输出的电压相同，各自承担1/3的总电压，如图12(a)所示。当负载功率PU∶PV∶PW=0∶1∶1时，各个子模块的功率也为PA1∶PA2∶PA3=0∶1∶1，此时uA1=0，uA2与uA3分摊总的输出电压，如图12(b)所示。当负载功率PU∶PV∶PW=0∶0∶1时，各个子模块的功率也为PA1∶PA2∶PA3=0∶0∶1，此时uA1=0，uA2=0，uA3独自承担总电压，如图12(c)所示。以图12(a)中的模块电压为额定值，则为了实现对不平衡功率的完全补偿，各个模块需要具备3倍于额定值的输出电压裕量。

图12 模块交流电压向量图Fig.12 Modules’ AC voltage vector

3.2 无功分量注入情况

CPC电力电子变压器可以通过在输入级中注入额外的无功分量来辅助各个模块实现功率均衡,此时一相桥臂的电压电流向量如图13所示。在这种控制策略下，不均衡功率是通过模块的电流裕量来补偿的，而不需要提高电压裕量。其原理与算法较为复杂，受限于篇幅，在本文中不做详细说明，可参考文献[16-19]。

图13 通过无功分量注入来消除过调制Fig.13 Reactive component injection in order to eliminate overmodulation

文献[19]中提出了一种简化的无功电压/电流注入算法，其核心是令三个模块的d轴电压相等，并测量桥臂内各个模块的功率与它们的平均功率，将与平均功率差异最大的模块的调制度设定为1，其他模块的调制度小于1，以避免过调制。其具体表达式为(忽略电感压降，忽略各个模块的直流电压差异)：

(5)

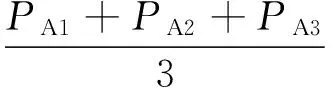
(6)

ΔPk=PAk-PAVR

(7)

(8)

式中，Ud1、Ud2、Ud3为三个模块d轴电压的有效值；UA为三个模块的总输出交流电压有效值；PAk(k=1,2,3)为三个模块的有功功率；ΔPk为该模块功率与平均功率的差值；VDC为各个模块的直流电压。

基于该算法，对系统所需的电流裕量进行了计算。通过简单的列表计算，可得到不同的额定调制度mrated[19](即额定工况下输入级变流器输出的交流电压峰值与直流电压幅值之比)下，系统补偿所有可能的不平衡功率情况所需的电流裕量。当mrated=0.8时，所需电流裕量为1.11；当mrated=0.85时，所需电流裕量为1.27；mrated=0.9时，所需电流裕量为1.53。相比于3.1节所述的3倍电压裕量而言，这一利用电流裕量的补偿策略较为实际。

4 自平衡电力电子变压器

由第3节的分析可知，SPC与CPC拓扑需要额外的电压/电流容量与较为复杂的控制策略来实现对不平衡的负载功率的补偿。这反映了模块化拓扑与负载不平衡补偿在本质上的冲突，仅从控制算法角度出发，很难得出既简单又具有良好效果的方案。为此，在CPC拓扑的基础上，本文对拓扑进行了改进，提出了自平衡拓扑。

将DAB中的两端口高频变压器改为多端口高频变压器，其中初级1个线圈，次级N个线圈，N的数量与输出级的相数相同。DAB变换器随之调整为MAB变换器，其中一次侧一个H桥，二次侧N个H桥。每个高频变压器的初级线圈通过MAB的初级H桥与输入级的一个模块连接；每个高频变压器的N个次级线圈通过MAB的N个次级H桥连接到输出级的N个相中。负载功率的不平衡仅会反映在高频变压器的二次侧，而不会反映在高频变压器的一次侧，因此对输入级没有任何影响。通过这种改进，输出功率可以自动平均分配到输入级的每个模块中去，不管输出级功率如何不均衡，输入级的每个模块功率都是自动均衡的。拓扑如图14所示。

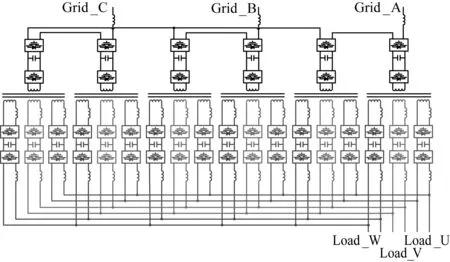
图14 基于多端口高频变压器的自平衡电力电子变压器Fig.14 Multi-winding HFT based self-balancing PET

MAB采用类似DAB的单电压环控制，通过调整各个次级线圈对应方波相对于初级线圈对应方波的相位差，来控制MAB二次侧各个端口的功率。控制框图如图15所示。

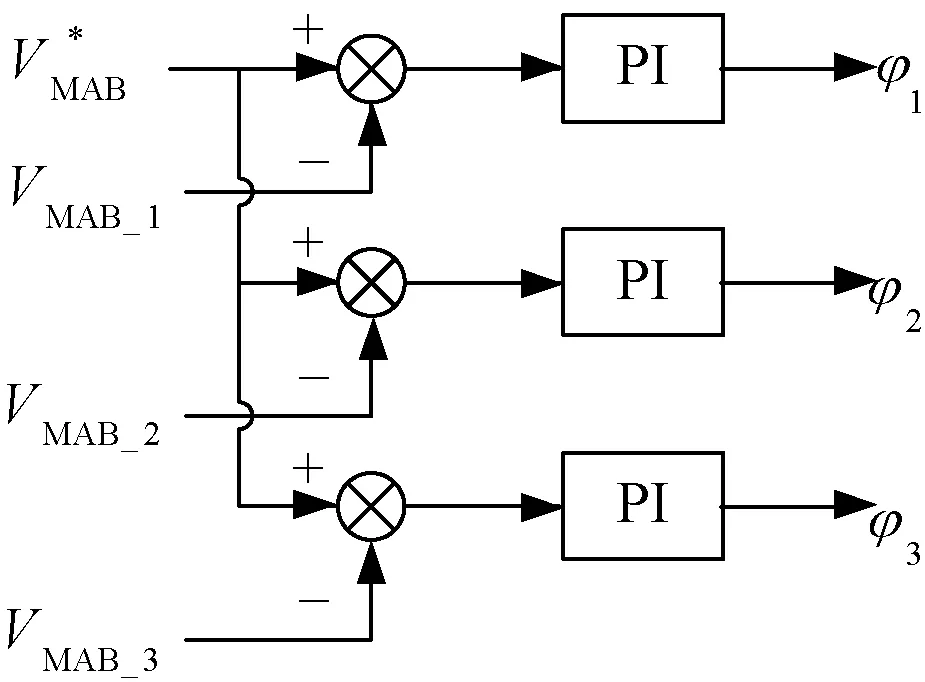
图15 多端口高频变压器二次侧H桥移相角控制Fig.15 MAB secondary H bridges’ phase shift control

鉴于大功率多端口变压器的制作难度很高，可以用多个常规高频变压器取代多端口高频变压器，形成一种模块化的全范围自平衡拓扑。每个输入级模块通过N个DAB变流器给输出级的N个相供电，同样能够实现输出级功率在输入级模块间的平均分配。其拓扑如图16所示。

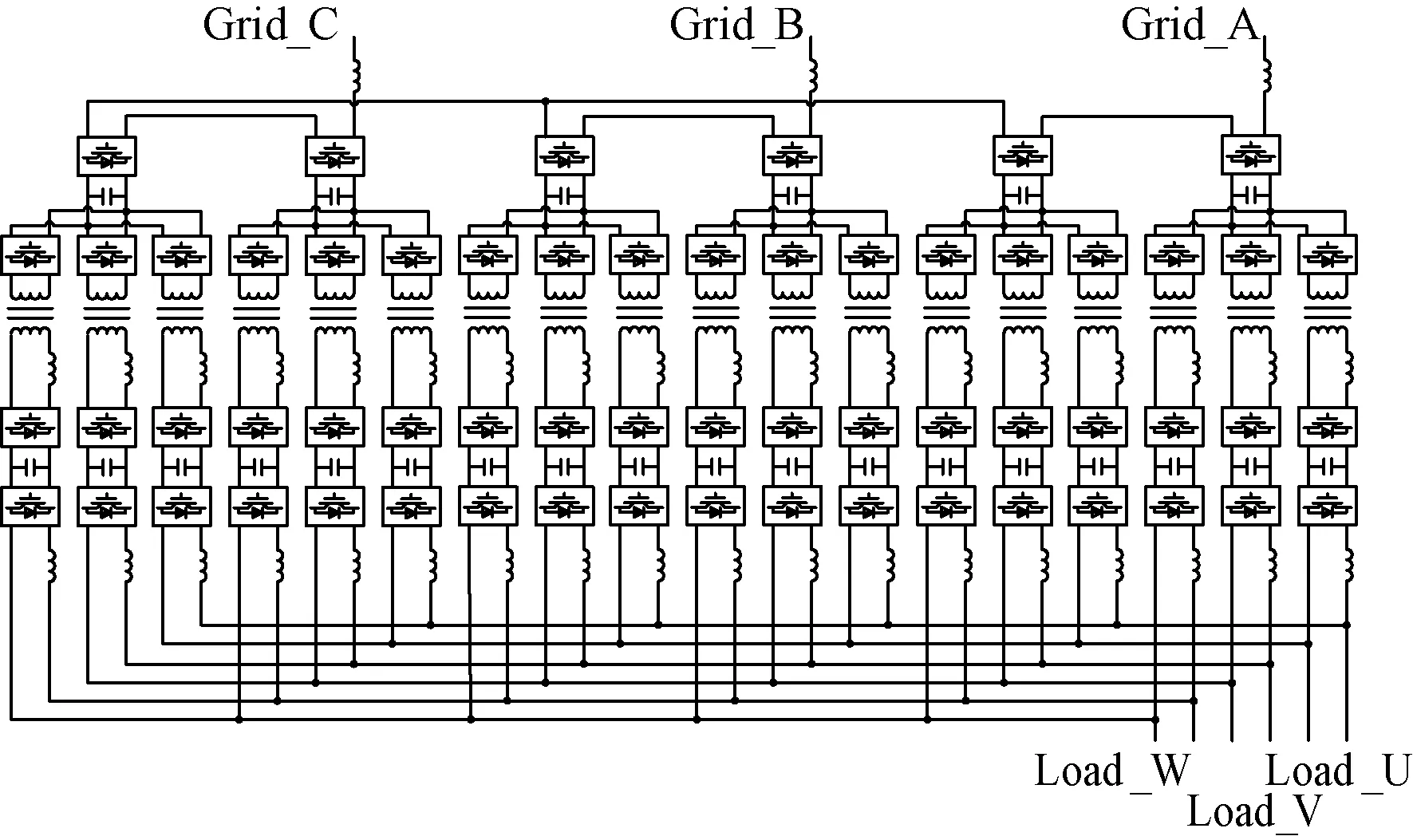
图16 模块化自平衡电力电子变压器Fig.16 Modular self-balancing PET

5 仿真验证

为了验证以上几种拓扑补偿不平衡负载的效果，在Matlab/Simulink中搭建了这些拓扑的仿真模型。输入电网电压为380V/220V，输入级每相3个模块，输出负载为3个，每个负载的额定功率5kW。对负载平衡与负载1∶1∶0不平衡的情况进行了仿真验证。

独立相连接拓扑及电流单位功率因数的交叉相连接拓扑中，每个模块的直流电压为200V，总直流电压为600V，额定调制度仅为0.52，远远低于工程实际中的正常额定调制度，这是因为这两种拓扑需要很大的电压裕量以补偿不平衡的负载功率。

自平衡拓扑与注入无功分量的交叉相连接中，每个模块的直流电压为125V，总直流电压为375V，额定调制度为0.83，为工程实际中的正常额定调制度，这是因为这两种拓扑不利用电压裕量补偿不平衡的负载功率，不需要过高的直流电压。

5.1 独立相连接

按照图4搭建输入级星型的独立相连接拓扑的仿真模型，根据图5的控制框图搭建输入级的控制环路，利用零序电压注入来实现不平衡负载功率补偿。

在0.4s之前，输出级的三相负载功率平衡，均为额定功率。0.4s之后，输出级中一相的负载跳变为0，负载功率变为1∶1∶0，如图17所示。

云计算是一种利用大规模低成本运算单元通过IP网络相连而组成的运算系统，用以提供各种计算和存储服务。由于具有高性能、低成本、可平滑扩展等优势，云计算为IT技术发展提供了新的技术手段和业务模式，不仅是企业降低建设和维护成本的重要手段，更为企业技术、业务和管理创新带来了新的契机。

图17 负载电流Fig.17 Load current

在后面的所有仿真中，负载跳变时刻均同样为0.4s，跳边后的负载功率比例同样为1∶1∶0。

图18显示了输入级的输入电流，在0.4s后仍为平衡，可见补偿算法的有效性。图19显示了输入级的各桥臂电压(滤除开关频率分量后)，可见由于零序电压的注入，桥臂电压不平衡。图20显示了各个模块的直流电压。

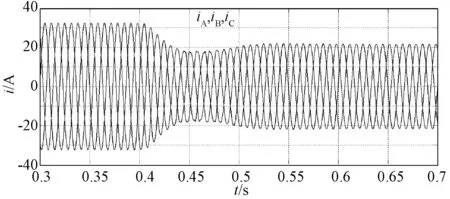
图18 电网电流(SPC)Fig.18 Grid current(SPC)

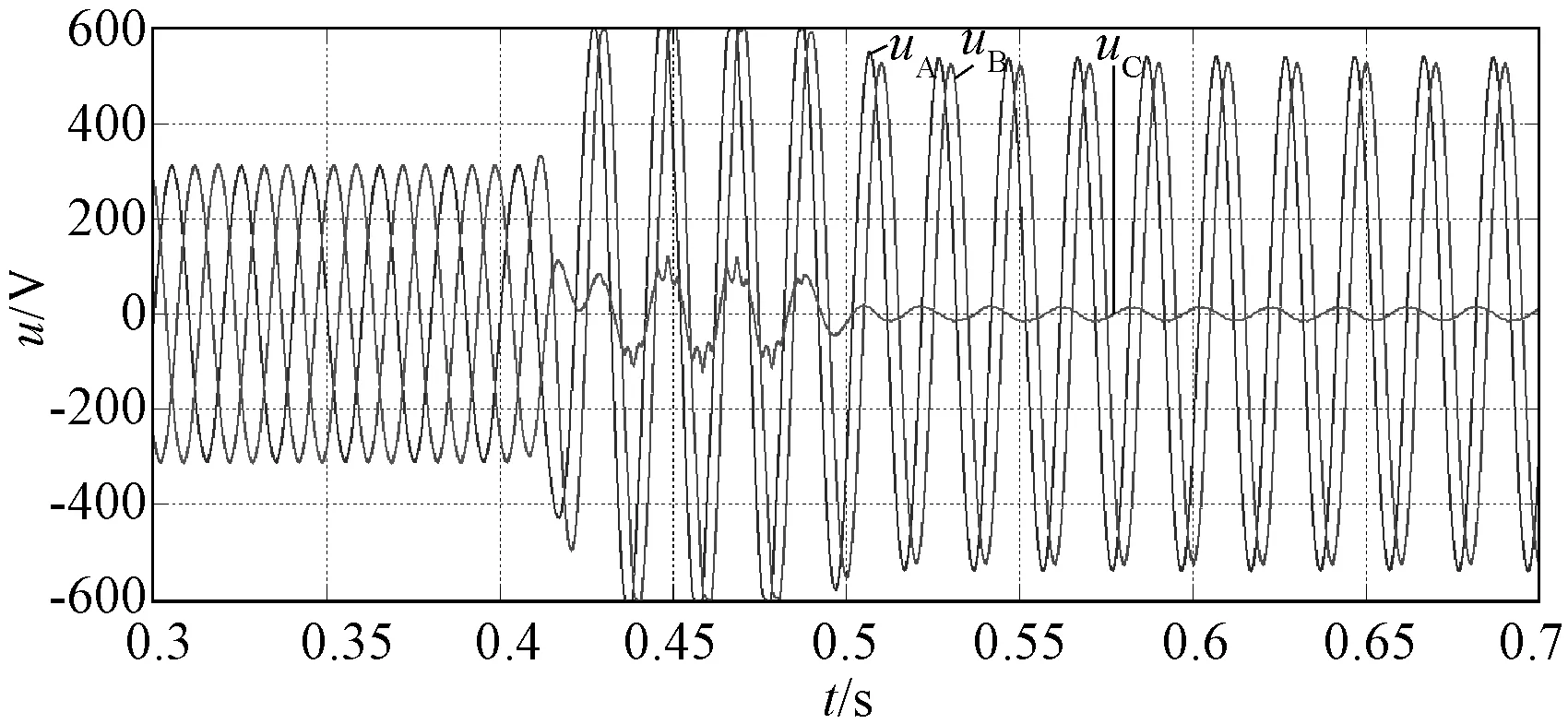
图19 输入级桥臂的交流端口电压(SPC)Fig.19 AC voltages of input stage clusters(SPC)

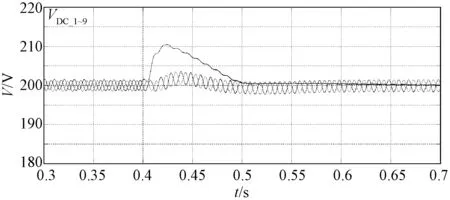
图20 输入级直流电压(SPC)Fig.20 DC voltages of input stage(SPC)

输入级三角形的独立相连接拓扑的波形可参考文献[15]，本文不再重复。

5.2 交叉相连接

5.2.1 电流单位功率因数情况

按照图11交叉相连接拓扑的仿真模型，输入级控制根据图5搭建，利用输入级各相内子模块的调制度来实现不平衡负载功率补偿。

图21 电网电流(CPC,电流单位功率因数)Fig.21 Grid current (CPC, unity power factor)

图22 输入级A相的模块交流端口电压(CPC,电流单位功率因数)Fig.22 AC voltages of modules in phase A (CPC, unity power factor)

图23 输入级直流电压(CPC,电流单位功率因数)Fig.23 DC voltages of input stage(CPC, unity power factor)

5.2.2 无功分量注入情况

按照图11的拓扑搭建仿真模型，输入级控制根据文献[19]及式(5)～式(8)搭建，利用无功分量注入来实现不平衡负载功率补偿。

图24显示了输入级的三相电流，在0.4s后仍为平衡，可见补偿算法的有效性。图25显示了输入级A相内的电网电压波形与电流波形，可见负载跳变后，系统中注入了一定的无功电流。图26为输入级A相的各个模块的交流侧电压(滤除开关频率分量后)，可见在负载变为不平衡后，无功注入算法令其中一个模块的调制度为1，即交流电压峰值为125V，与直流电压相等，同时另两个模块的调制度小于1，与3.2节中描述的一致。图27显示了各个模块的直流电压。

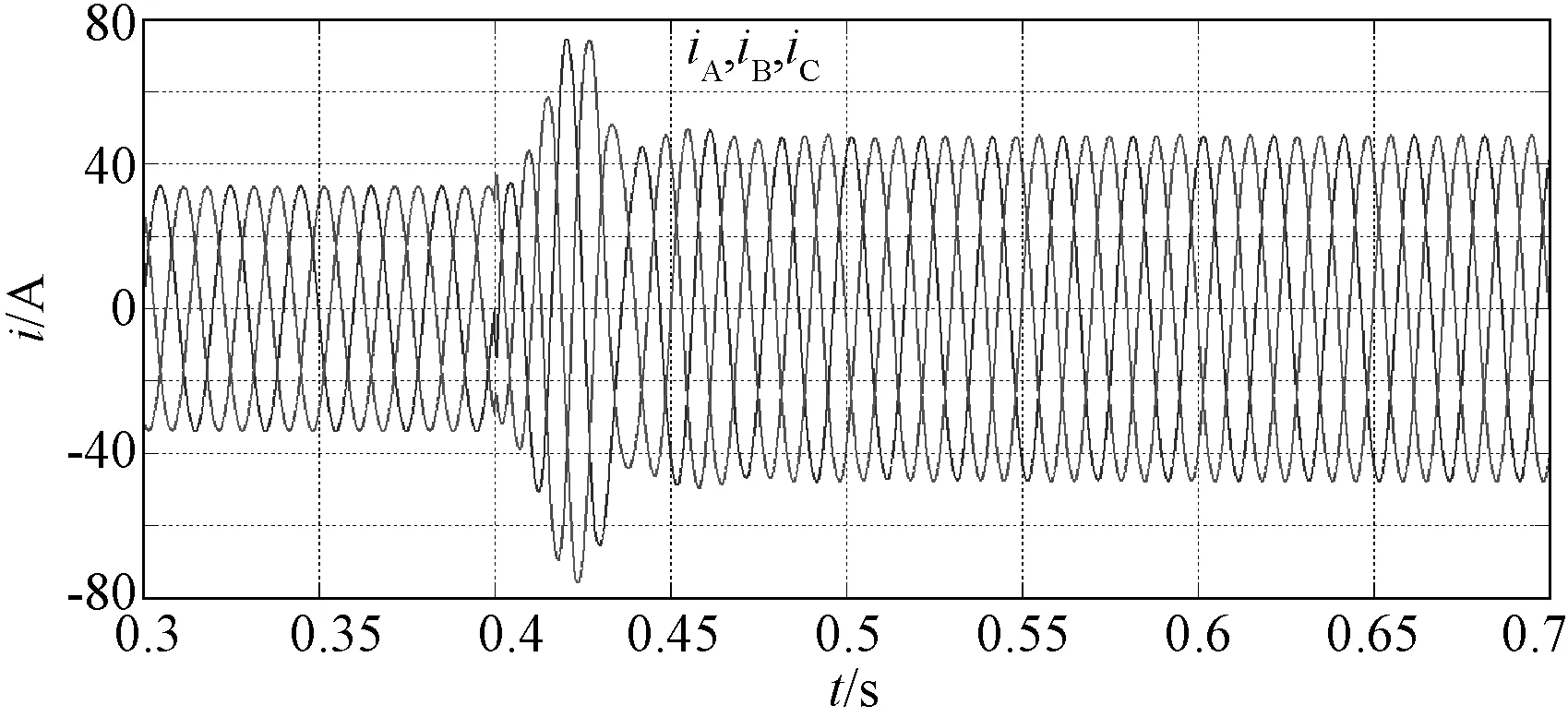
图24 电网电流(CPC,无功分量注入)Fig.24 Grid current(CPC, reactive component injection)

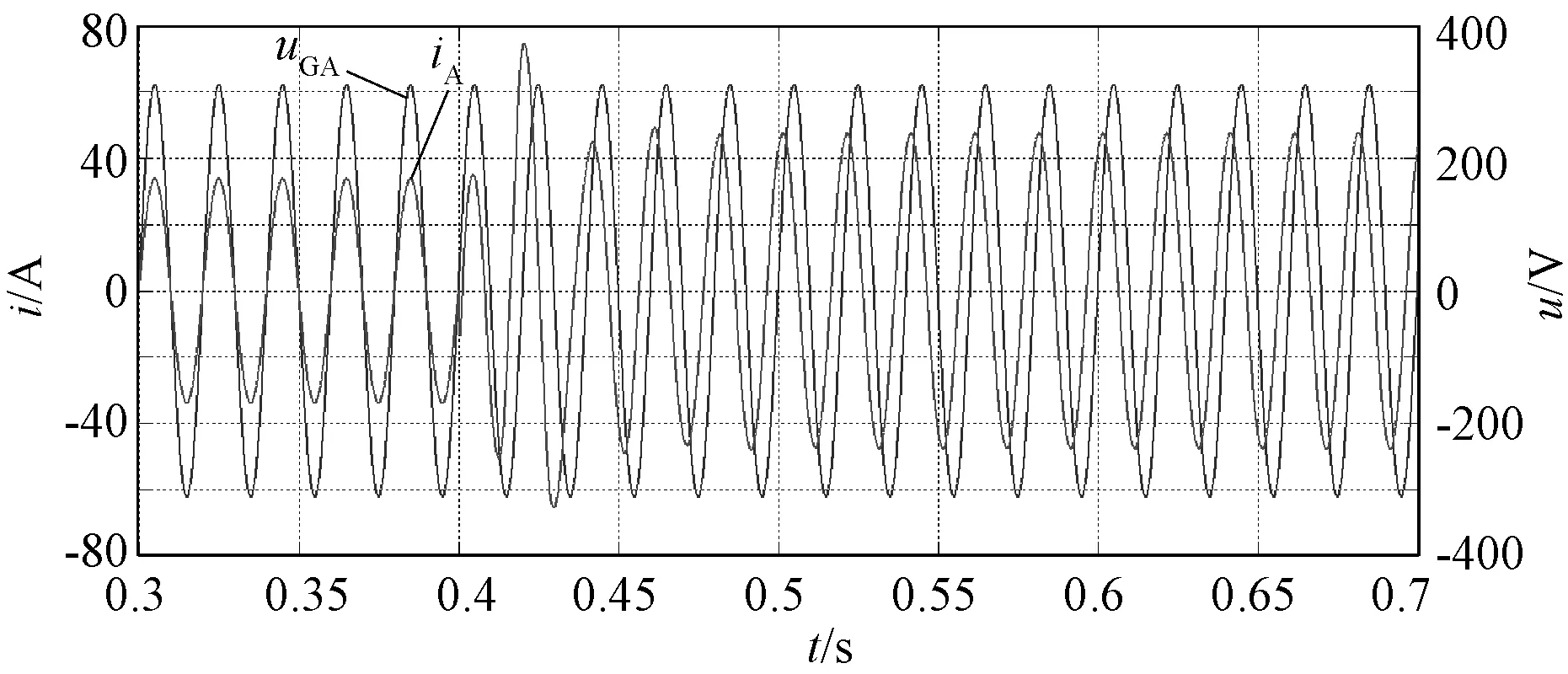
图25 A相电网电压与电流(CPC,无功分量注入)Fig.25 Phase A grid voltage and current (CPC, reactive component injection)

图26 输入级A相的模块交流端口电压 (CPC,无功分量注入)Fig.26 AC voltages of modules in phase A (CPC, reactive component injection)

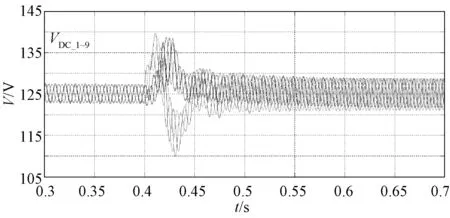
图27 输入级直流电压(CPC,无功分量注入)Fig.27 DC voltages of input stage(CPC, reactive component injection)

5.3 基于多端口高频变压器的自平衡电力电子变压器

按照图14拓扑搭建基于多端口高频变压器的自平衡拓扑的仿真模型。图28显示了输入级的输入电流，在0.4s后仍为平衡，可见该拓扑具有补偿不平衡负载的能力。图29显示了拓扑中某一个高频变压器的二次侧电流。其中图29(a)显示了负载跳变之前，负载平衡时的二次侧电流，此时的二次侧电流波形相同，对应的三路输出功率也相同；图29(b)显示了负载跳变之后，负载不平衡时的二次侧电流，此时的二次侧电流波形不同，对应的三路输出功率也不同。负载功率的不平衡只会体现在高频变压器的二次侧线圈中，不会反映到一次侧，从而实现了不平衡负载功率的补偿。图30显示了各个模块的直流电压。

图28 电网电流(自平衡PET)Fig.28 Grid current (self-balancing PET)

图29 多端口高频变压器的二次侧线圈电流Fig.29 Secondary side currents of multi-winding high frequency transformer

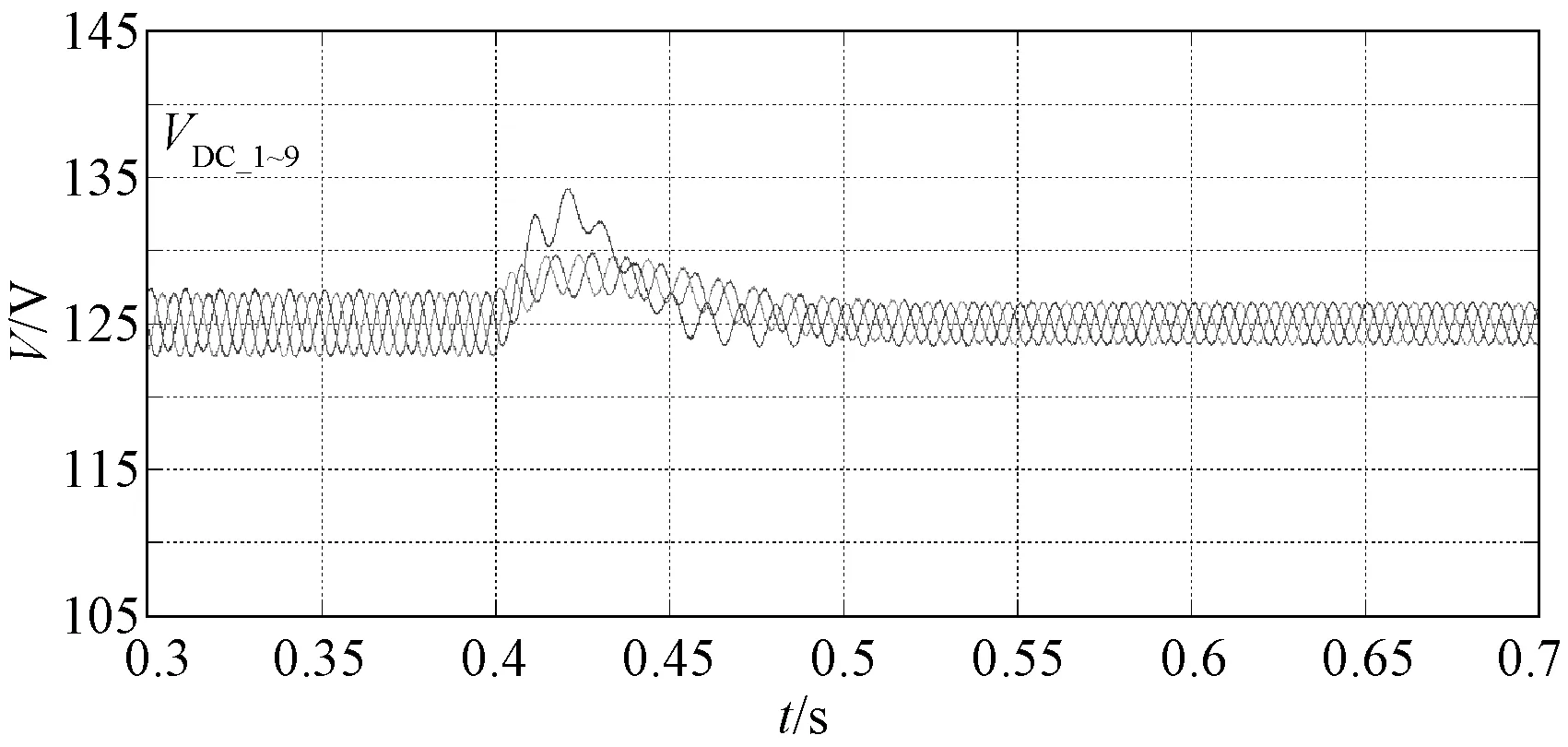
图30 输入级直流电压(自平衡PET)Fig.30 DC voltages of input stage (self-balancing PET)

图16所示的模块化自平衡拓扑与本拓扑的输出波形相同，因此在本文里不再另做仿真验证。

6 拓扑的对比

3种拓扑的复杂度对比如表1所示。从拓扑本身的复杂度来看，自平衡拓扑>交叉相连接拓扑>独立相连接拓扑。从控制算法复杂度来看，交叉相连接+无功分量注入算法>独立相连接+零序注入算法>交叉相连接+模块调制度算法>自平衡拓扑控制算法。

不同拓扑/算法下，为了补偿全范围不平衡负载功率，输入级模块所需的电压/电流裕量如表2所示。星型+独立相连接拓扑的输入级模块需要3倍的电压裕量，三角形+独立相连接拓扑的输入级模块需要1.15倍的电流裕量；交叉相连接拓扑在不注入无功分量，单纯利用模块调制度实现不平衡负载补偿时，输入级模块需要3倍的电压裕量；交叉相连接采用无功分量注入实现不平衡负载补偿时，输入级模块需要1.11～1.53倍电流裕量，这一数字取决于系统的额定调制度[19]；自平衡拓扑利用拓扑本身实现不平衡补偿，输入级模块不需要额外的电压或者电流裕量。

表1 拓扑对比

表2 输入级模块所需电压/电流裕量对比

值得注意的是，交叉相连接+模块调制度方案虽然难以用于补偿全范围负载不平衡，但在系统对负载不平衡的补偿能力要求较低的情况下，是最简单实用的方案。

7 结论

本文研究三种模块化多输出电力电子变压器拓扑的不平衡负载补偿功能。对三种拓扑实现不平衡负载补偿的原理与算法进行了研究，对三种拓扑为实现大范围不平衡负载补偿所需的额外电压/电流容量进行了比较，并进行了仿真验证。

[1] Kolar J W, Ortiz G. Solid-state-transformers: Key components of future traction and smart grid systems[A]. International Power Electronics Conference - ECCE Asia [C]. 2014. 22-35.

[2] 毛承雄，范澍，王丹，等(Mao Chengxiong, Fan Shu, Wang Dan, et al.)．电力电子变压器的理论及其应用(Theory of power electronic transformer and its applications) [J]. 高电压技术(High Voltage Engineering)，2003，29(10)：4-6.

[3] Dujic D, Zhao C, Mester A, et al. Power electronic traction transformer-Low voltage prototype [J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5522-5534.

[4] She X, Huang A Q, Wang F, et al. Wind energy system with integrated functions of active power transfer, reactive power compensation, and voltage conversion [J]. IEEE Transactions on Industrial Electronics, 2012, 60(10): 4512-4524.

[5] She X, Yu X, Wang F, et al. Design and demonstration of a 3.6-kV-120-V/10-kVA solid-state transformer for smart grid application [J]. IEEE Transactions on Power Electronics, 2013, 29(8): 3982-3996.

[6] Qin Hengsi, Kimball Jonathan W. Solid-state transformer architecture using AC-AC dual-active-bridge converter [J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3720-3730.

[7] Basu Kaushik, Mohan Ned. A single-stage power electronic transformer for a three-phase PWM AC/AC drive with source-based commutation of leakage energy and common-mode voltage suppression [J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 5881-5893.

[8] Prasai Anish, Chen Hao, Moghe Rohit, et al. Dyna-C: Experimental results for a 50 kVA 3-phase to 3-phase solid state transformer [A]. 2014 IEEE Applied Power Electronics Conference and Exposition-APEC 2014 [C]. 2014. 2271-2277.

[9] Hugo Nicolas, Stefanutti Philippe, Pellerin Marc, et al. Power electronics traction transformer [A]. European Conference on Power Electronics and Applications [C]. 2007. 1-10.

[10] Drbek Pavel, Peroutka Zdenek, Pittermann Martin, et al. New configuration of traction converter with medium-frequency transformer using matrix converters [J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5041-5048.

[11] Madhusoodhanan Sachin, Tripathi Awneesh, Bhattacharya Subhashish, et al. Solid-state transformer and MV grid tie applications enabled by 15 kV SiC IGBTs and 10 kV SiC MOSFETs based multilevel converters [J]. IEEE Transactions on Industry Applications, 2015, 51(4): 3343-3360.

[12] 李子欣，王平，李耀华，等(Li Zixin, Wang Ping, Li Yaohua, et al.). 面向中高压智能配电网的电力电子变压器研究(Research on medium-and high-voltage smart distribution grid oriented power electronic transformer) [J]. 电网技术(Power System Technology), 2013, 37(9): 2592-2601.

[13] 兰征，涂春鸣，肖凡，等(Lan Zheng, Tu Chunming, Xiao Fan, et al.). 电力电子变压器对交直流混合微网功率控制的研究(The power control of power electronic transformer in hybrid AC-DC microgrid)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2015, 30(23): 50-57.

[14] Maharjan L, Inoue S, Akagi H, et al. State-of-charge (SOC) balancing control of a battery energy storage system based on a cascade PWM converter [J]. IEEE Transactions on Power Electronics, 2009, 24(6): 1628-1636.

[15] Wang X, Liu J, Ouyang S, et al. Research on unbalanced-load correction capability of two power electronic transformer topologies [J]. IEEE Transactions on Power Electronics, 2015, 30(6): 3044-3056.

[16] Rezaei M, Iman-Eini H, Farhangi S. Grid-connected photovoltaic system based on a cascaded H-Bridge inverter [J]. Journal of Power Electronics, 2012, 12(4): 578-586.

[17] Liu L, Li H, Xue Y. A coordinated active and reactive control strategy for grid-connected cascaded photovoltaic (PV) system in high voltage high power applications [A]. Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC) [C]. 2013. 1301-1308.

[18] Liu Liming, Li Hui, Xue Yaosuo, et al. Decoupled active and reactive power control for large-scale grid-connected photovoltaic systems using cascaded modular multilevel converters [J]. IEEE Transactions on Power Electronics, 2015, 30(1): 176-187.

[19] Ouyang Shaodi, Liu Jinjun, Song Shuguang, et al. Reactive component injection control of the modular multi-output power electronic transformer [A]. 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC) [C]. 2016. 1-7.

Comparison of several modular multi-output power electronic transformer topologies on unbalanced load compensation capability

OUYANG Shao-di, LIU Jin-jun

(School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Power Electronic Transformer (PET) can provide not only voltage level transform and isolation, but also some additional functions. The multi-output function, enabling the PET to drive multiple loads, is one of these additional functions. When driving multiple loads, there will be unbalanced load condition, which would bring challenge to the PET’s operation. Therefore, topologies and control strategies suitable for multi-load PET needs to be studied. This paper compares three different topologies on unbalanced load compensation capability, including seperate-phase-connected topology, cross-phase-connected topology and self-balancing topology. The seperate-phase-connected topology handles the unbalanced load by zero sequence voltage/current injection into the input stage. The cross-phase-connected topology handles the unbalanced load by adjusting the modulation indexes of modules within a input stage cluster or injecting reactive component into the input stage. The self-balancing topology handles the unbalanced load by the topology itself and the use of multi-winding high frequency transformer. This paper analyzes the operation principle and control strategy of these three topologies. The unbalanced load compensation function of the three topologies is verified by Simulink.

power electronic transformer; multi-output; unbalanced load; topology

2017-03-02

欧阳少迪(1989-), 男, 湖北籍, 博士研究生, 研究方向为电力电子变压器、大功率DC-DC变流器； 刘进军(1970-), 男, 湖南籍, 教授, 博士, 研究方向为电力电子技术在电能质量控制及电力系统中的应用、电力电子电路和系统的建模、分析与控制、电力电子变压器、模块化多电平变流器等。

TM41

A

1003-3076(2017)05-0011-10