混凝土弹塑性分析的新模型

柯 江

(陕西理工大学土建学院，陕西 汉中 723001)



混凝土弹塑性分析的新模型

柯 江

(陕西理工大学土建学院，陕西 汉中 723001)

针对混凝土弹塑性分析的平面应力问题和空间问题进行了分析，基于等效外力下的变形相同，提出了一个桁架单元新模型，并给出了实例验证，与实体单元的计算结果吻合良好。

桁架单元,本构关系,平面应力，极限承载力

混凝土弹塑性分析的传统方法涉及到多轴强度准则、多轴弹塑性本构关系，混凝土的多轴强度准则不下几十个，可以精确描述混凝土性能的多轴弹塑性本构关系模型，目前还不存在。笔者为了简化计算，提出了一个由若干杆件组成的桁架单元新模型，采用新模型计算各向同性、正交各向异性的线弹性材料，后来又推广到一般的弹塑性材料，并给出了确定固体内任意一点的应力应变的方法[1-5]，本文将给出另一种混凝土(也适用于岩石等其他脆性材料)的弹塑性分析新模型及计算实例。

1 桁架单元新模型

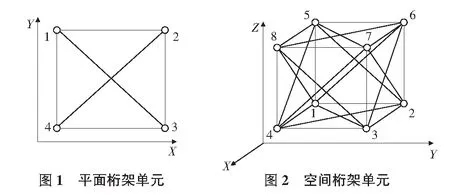
材料参数：εc0，εcu,εcmax分别为材料单轴受压时的峰值应变、下降段的极限压应变、二次上升段的最大压应变，εtu为材料单轴受拉时的极限拉应变；ft,fc,τ0,E分别为抗拉强度、抗压强度、抗剪强度、弹性模量；γmax为材料纯剪切时的最大剪应变；εcu应满足εcu≥2εc0+ft/E。新单元模型包括平面桁架单元(图1适用于平面应力问题)与空间桁架单元(图2适用于空间问题)，其建立方法与文献[5]相同，只是物理意义不同，导致其应力应变曲线不一样。

1.1 平面应力问题

表1～表3分别为材料单轴受压、单轴受拉、纯剪切时的应力应变曲线，而桁架单元中的平行杆、斜杆的应力应变曲线见表4～表7，表中的参数，k1=3k5ft/fc；0≤k2≤1；k3≥k2,建议取50；0≤k4≤1；1/3≤k5<1；k1≤k6≤(4/3)-(ft/fc)；εtu-k4ft/(3E)<γmax<π/2；εtu=εcu-εc0+(3-2k4)ft/E。

表1 材料单轴受压(一)

表2 材料单轴受拉(一)

表3 材料受剪(一)

表4 平行杆受压(一)

表5 平行杆受拉(一)

表6 斜杆受压(一)

表7 斜杆受拉(一)

1.2 空间问题

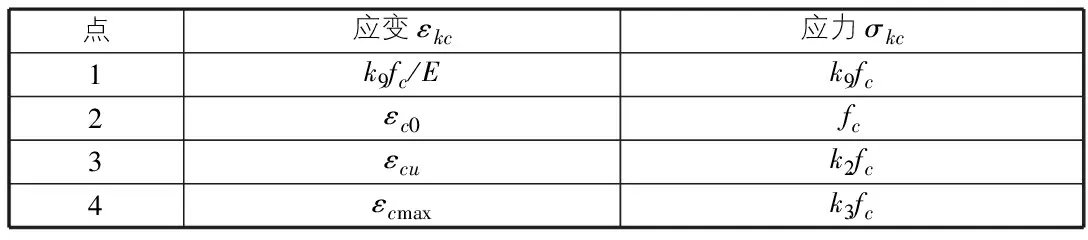
表8 材料单轴受压(二)

表9 材料单轴受拉(二)

表10 材料受剪(二)

表11 平行杆受压(二)

表12 平行杆受拉(二)

表8～表10分别为材料单轴受压、单轴受拉、纯剪切时的应力应变曲线，而桁架单元中的平行杆、斜杆的应力应变曲线见表11～表14。表中的参数，k4≤k7≤1；max{k4,(5k7-2)/3}≤k8≤(5k7-2k4)/3，建议取k8=k7；k9=1.5ft/fc；k9≤k10≤2.5-(2+1.5k8)ft/fc；εtu-0.25k4ft/E<γmax<π/2；εtu=εcu-εc0+(2+0.75k8-1.75k4)ft/E。

表13 斜杆受压(二)

表14 斜杆受拉(二)

2 计算实例与说明

一个混凝土简支梁，跨度320 mm，截面高度80 mm、宽度1 mm，弹性模量E=30 000 N/mm2，泊松比v=1/3，fc=14.3 N/mm2，ft=τ0=1.43 N/mm2，εc0=0.002，εcu=εcmax=0.006，εtu=0.004 142，γmax=0.1，跨中施加位移荷载求极限承载力，分别按平面应力实体单元模型与平面桁架单元模型来计算，单元尺寸均为10 mm×10 mm,两种单元都划分为256个单元，平行杆截面面积为3.75 mm2，斜杆截面面积为5.303 3 mm2，平面应力实体单元的应力应变曲线按表1,表2取值，桁架单元中平行杆、斜杆的应力应变曲线按表4～表7取值，其中k1=0.24，k2=k3=0.1，k4=0.01，k5=0.8，k6=0.5。采用有限元软件计算可得：平面应力实体单元方法得到的极限承载力为39.9 N，平面桁架单元方法得到的极限承载力为35.9 N，两者吻合良好。另外说明：文献[5]中，“材料受剪、斜杆受压”的应力应变曲线最后1点的应力，分别采用本文表3,表6,表10,表13的最后1点的应力，则会具有更加直观的物理意义。

3 结语

目前，混凝土的弹塑性计算问题非常复杂，而采用本文的桁架单元新模型，对桁架单元的各杆件赋予截面面积、弹性模量、受压及受拉应力应变曲线，则相当于对桁架单元赋予了一个多轴强度、多轴本构关系，经大量计算，多轴强度与试验资料吻合良好，而桁架单元的弹塑性多轴本构关系的合理性，可以从大量计算实例中得到验证。

[1] 过镇海,时旭东.钢筋混凝土原理和分析[M].北京：清华大学出版社，2003.

[2] 柯 江.实体结构求解的新方法[J].山西建筑，2008，34(9):112-113.

[3] Ke Jiang.A New Element Model of Solid Bodies[J].Applied Mechanics and Materials,2012(174-177):2115-2118.

[4] Ke Jiang.Applications of a New Element Model of Solid Bodies in Plasticity[J].Advanced Materials Research,2013(690-693):1800-1805.

[5] 柯 江.弹塑性固体的新单元模型[J].山西建筑,2016,42(31):46-47.

A new model for elasto-plastic analysis of concrete

Ke Jiang

(SchoolofCivilEngineeringandArchitecture,ShaanxiUniversityofTechnology,Hanzhong723001,China)

For the plane stress problem and the spatial problem of the elasto-plastic analysis of concrete, a new truss element model is presented by using the deformations under the equivalent external forces are the same. Some examples is given, which is in good agreement with the calculation results of the solid element.

truss element, constitutive relation, plane stress, ultimate bearing capacity

1009-6825(2017)11-0049-02

2017-01-22

柯 江(1976- )，男，硕士，讲师

TU311.41

A