平滑风电功率波动的混合储能系统容量优化配置

靳雯皓,刘继春

(四川大学电气信息学院，四川 成都 610065)

平滑风电功率波动的混合储能系统容量优化配置

靳雯皓,刘继春

(四川大学电气信息学院，四川 成都 610065)

风电输出功率具有波动性，为减小其对电力系统运行的影响，提高电力系统的电能质量，提出了平抑功率波动的混合储能系统容量优化配置方法。采用滑动平均法滤除波动功率，平滑风电输出功率，滑动平均法中窗口长度的选择将影响功率平滑效果及混合储能系统容量配置，依据并网功率波动限制为约束确定窗口长度值，实现其最优选择。采用频谱分析的方法分解波动功率，以年均综合成本最小为目标函数确定超级电容器和蓄电池各自补偿频段，进而确定其实时充放电功率。最后，建立了考虑蓄电池寿命损耗的混合储能系统成本模型，通过案例分析验证本方案的可行性以及经济优越性。

超级电容器；蓄电池；混合储能系统；寿命损耗；滑动平均法；频谱分析

0 引言

风力发电是解决当前能源问题的重要途径[1]。由于风电出力具有随机性、间接性和不可控性等缺点，大规模风电并网会对电网造成不利的影响，甚至严重危害电力系统正常运行[2]。因此，如何平抑风电功率波动，提高风电渗透率，实现风电资源大规模并网是目前亟待解决的问题。

储能系统作为微电网的重要组成部分，在平抑风电功率波动、提高电力系统电能质量、保证电力系统供电可靠性等方面发挥了重要作用。储能系统可以分为单一储能系统和混合储能系统[3-4]。单一储能系统由功率型储能设备或能量型储能设备组成，功率型储能设备功率密度大，能量密度小，能量型储能设备能量密度大，功率密度小，因而其无法同时兼顾功率密度和能量密度的需求[5]。功率型储能设备和能量型储能设备组成的混合储能系统可以实现2种储能设备的优势互补，因而得到了广泛应用。文献[6]分析了单一超级电容器储能及单一蓄电池储能平抑风电功率波动的不足，并建立了基于超级电容器和蓄电池组成的混合储能系统模型，算例分析验证了混合储能系统相较于单一储能系统的优越性。文献[7]采用一阶低通滤波器平滑风电输出功率波动，考虑到超级电容器和蓄电池不同储能特性，分别承担功率波动中的高频波动和低频波动，以备用需求为约束条件实现系统运行成本最优。文献[8]提出了一种在超级电容器和蓄电池运行允许范围内实现超级电容器优先充放电的控制策略，采用量子遗传算法优化混合储能系统容量配置，实现储能系统成本投资最小。文献[9]提出一种混合储能系统容量优化方法，采用经验模态分解技术将风电输出功率分解为高频和低频功率波动分别由超级电容器和蓄电池平抑，采用神经网络模型优化混合储能系统容量配置。文献[10]提出了一种基于储能系统荷电状态反馈的功率分配策略，根据储能系统荷电状态值实时调整低通滤波器的滤波时间常数，实现其对超级电容器和蓄电池充放电功率的控制。

图1 微网系统结构Fig.1 Structure of micro-grid system

本文采用滑动平均法平滑风电输出功率，以并网功率波动限制为约束确定窗口长度值。采用频谱分析的方法分解波动功率，以年均综合成本最小为目标函数确定超级电容器和蓄电池充放电功率。最后，建立考虑蓄电池寿命损耗的混合储能系统成本模型，通过案例分析验证本方案可行性及相对于单一储能方案的经济优越性。

1 微网模型

图1为典型风-储系统模型，由风电机组、超级电容器、蓄电池、DC/AC变换器、DC/DC变换器、中央控制器等组成。其中，超级电容器和蓄电池组成混合储能系统，分别用于平抑高频功率波动和低频功率波动，先通过DC/DC变换器接入直流母线，汇总后通过DC/AC变换器接入交流母线。中央控制器根据实时运行信息调节储能系统工作状态。

图中：Pw(t)表示风电机组t时刻输出功率；Phess(t)表示混合储能系统t时刻充放电功率；Pcap(t)、Pbat(t)分别表示超级电容器和蓄电池t时刻充放电功率，其值为正表示储能装置处于放电状态，其值为负表示储能装置处于充电状态；Pgrid(t)表示t时刻并入电网功率，表达式为

(1)

混合储能系统充放电功率为

(2)

2 风电功率波动的平滑控制

2.1 功率波动指标

根据国家电网公司标准《风电场接入电力系统技术》的规定，最大功率波动率分为1 min间隔功率波动率和10 min间隔功率波动率，都应满足电网调度部门的限制要求，相关波动限制如表1所示。

表1 风电场最大功率波动标准

本文所研究系统的风电场装机容量为33 MW，则1 min间隔最大功率波动限制值为3.3 MW，即最大功率波动率不能超过10%；10 min间隔最大功率波动限制值为11 MW，即最大功率波动率不能超过33.3%。

最大功率波动率指在相应时间间隔内功率波动的峰谷差值占风电场装机容量的百分比，本文采样时间间隔为1 min，则1、10 min时间间隔的最大功率波动率表达式为

(3)

(4)

式中：ηt,1min表示1 min时间间隔最大功率波动率；ηt,10min表示10 min时间间隔最大功率波动率；PN表示风电场装机容量，P1min、P10min的表达式为

(5)

(6)

2.2 平滑控制策略

本文采用滑动平均法平滑风电输出功率，提高风电资源的渗透率。通过该方法平滑控制后，可以得到平滑的并网功率，其表达式为

(7)

窗口长度T是滑动平均法的重要参数，其值选择过大，将导致并网功率过于平滑，储能系统容量配置过大，投资成本增加；其值选择过小，将导致并网功率平滑程度低，危害电力系统正常运行。

本文以1、10 min时间间隔下并网功率波动限制为约束，分别确定满足2种时间间隔下波动限制的最小窗口长度，选择较小值作为固定窗口长度，以此在保证并网功率满足波动限制要求的前提下，可实现混合储能系统容量优化配置。

3 混合储能系统模型

3.1 功率分配

通过滑动平均法平滑控制得到了满足波动限制要求的并网功率，根据式(1)，混合储能系统平抑的波动功率表达式为

(8)

采用频谱分析的方法，将波动功率分解为高频功率波动和低频功率波动由混合储能系统平抑。其中，超级电容器平抑高频功率波动，蓄电池平抑低频功率波动。

对波动功率Phess(t)进行傅里叶变换，可得幅度Shess和频率fhess的表达式为

(9)

将超级电容器和蓄电池各自补偿频段内的频域数据转换至时域，即可得储能装置实时充放电功率。由此可见，补偿频段的划分将影响超级电容器和蓄电池的功率分配，进而会影响混合储能系统容量配置。

假设超级电容器的补偿频段为fcap，则超级电容器补偿频段的幅值为Scap，令补偿频段内的幅值不变，补偿频段外的幅值置0。

(10)

对Scap进行反傅里叶变换，即可得超级电容器的充放电功率为

(11)

式中IDFT(Scap)表示对Scap进行傅里叶反变换运算。

根据式(2)，蓄电池的充放电功率为

(12)

3.2 容量配置

储能装置在充放电过程中会有一定损耗，考虑其充放电效率后的实时功率表达式为

(13)

式中Px(n)表示储能装置n时刻充放电功率，x=(1,2)时分别表示超级电容器和蓄电池，其中η为

(14)

式中：ηc表示充电效率；ηd表示放电效率。

本文设定储能装置实际充放电功率Pn绝对值的最大值即为其额定功率。则各个时刻累积能量为

(15)

式中：En、En+1分别表示储能系统n、n+1时刻累积能量；Δt表示时间间隔。

储能装置的额定容量可由其荷电状态(SOC)限制值和累积能量值共同确定，表达式为

(16)

3.3 寿命分析

超级电容器的使用寿命可达20年，远高于蓄电池的循环使用寿命，因此本文设定超级电容器使用年限为固定值。蓄电池最大充放电次数与放电深度关系表达式为

Nbat=-3 278D4-5D3+12 823D2-

14 122D+5 112

(17)

式中：D表示放电深度；Nbat表示对应放电深度下的循环使用次数。

蓄电池充放电循环1次，其寿命损耗占总寿命百分比为1/Nbat，则1个研究周期内，蓄电池寿命损耗为

(18)

式中：Nd表示研究周期内蓄电池充放电次数；Nloss表示研究周期内寿命损耗总值。

由此可得，蓄电池使用寿命表达式为

(19)

式中：Ny表示运行年限；Ts表示研究周期时长。

4 储能系统成本分析

4.1 目标函数

本文建立了考虑蓄电池寿命损耗的混合储能系统成本模型，主要考虑初始投资成本、寿命损耗成本及运行维护成本。

(1) 初始投资成本为

(20)

式中：Pcap、Ecap、Pbat、Ebat分别表示蓄电池和超级电容器的额定功率和额定容量；α1、α2表示超级电容器的功率成本系数和容量成本系数；β1、β2表示蓄电池功率成本系数和容量成本系数。

(2) 寿命损耗成本为

(21)

(3) 运行维护成本为

(22)

式中：k1、k2分别表示超级电容器和蓄电池运行维护成本系数。

混合储能系统年均综合成本最小，即目标函数表达式为

minC=min(C1+C2+C3)

(23)

4.2 约束条件

超级电容器充放电功率约束为

(24)

超级电容器荷电状态约束为

(25)

蓄电池充放电功率约束为

(26)

蓄电池荷电状态约束为

(27)

5 案例仿真

本文以装机容量为33 MW的风电场某日历史数据为例，验证本方案的可行性及经济优越性，系统相关参数如表2所示。

表2 系统相关参数

风电功率具有波动性，直接接入电力系统会危害电力系统正常运行，本文采用滑动平均法平滑风电输出功率。窗口长度是滑动平均法的重要参数，其值的选取不仅影响并网功率平滑效果，而且影响混合储能系统的成本投资。因此，本文以1、10 min时间间隔下并网功率波动限制为约束确定窗口长度值，使其在保证并网功率满足波动限制要求的前提下，进一步可实现混合储能系统容量优化配置。不同窗口长度下1、10 min时间间隔的最大功率波动率变化如图2所示。

图2 1、10 min时间间隔的最大功率波动率Fig.2 1,10 min interval maximum power fluctuation rate

选取T=5、10、16、20得到最大功率波动率如表3所示。

表3 最大波动率统计表

从图2和表3可以看出，随着窗口长度增加，1、10 min时间间隔下最大波动率都大幅度下降。当窗口长度增至5时，1 min时间间隔最大波动率为9.688%满足并网要求，但10 min时间间隔最大波动率为38.165%不能满足并网要求。当窗口长度增至16时，10 min时间间隔最大波动率为32.19%满足并网要求，即为同时满足波动限制要求的最小窗口长度。当窗口长度为20时，1、10 min时间间隔最大波动率变得更小，但此时混合储能系统需要平抑的波动功率增加，储能成本投资增加，因此，为了优化储能系统容量配置，本文选取固定窗口长度值为16，可保证并网功率同时满足1、10 min时间间隔的波动限制要求，进而降低混合储能系统所需平抑波动功率，实现其容量优化配置。

风电及并网功率1、10 min时间间隔下波动率分布区间的概率如图3所示。

图3 1、10 min时间间隔的波动率分布区间概率Fig.3 1,10 min interval volatility distribution interval probability

从图3可以看出，通过滑动平均法控制，1 min时间间隔下45.50%的波动率处于[0%～1%]内，98.46%的波动率控制在5%以下；10 min时间间隔下37.75%的波动率为[0%～10%]，98.10%的波动率控制在30%以下。相较于原始风电功率，并网功率波动率得到了有效控制。

为了分析波动功率的波动情况，选取最优频率分断点，本文对滑动平均法滤除的波动功率数据进行离散傅里叶变换，得到其幅频特性曲线如图4所示。

图4 幅频特性曲线Fig.4 Curve of amplitude frequency characteristics

从图4可以看出，波动幅值大的低频波动分量主要集中在0～3 mHz，在此之间选择频率分断点，即可实现混合储能系统功率分配。本文采用试频法，选取不同分断点频率，比较对应频率下混合储能系统年均综合成本，选择年均综合成本最小的频率分断点。不同分断点频率下的系统年均综合成本如图5所示。

图5 不同分断点频率下的系统年均综合成本Fig.5 Annual comprehensive cost of system under different breaking point frequency

由图5可知，混合储能系统年综合成本随着频率分断点的增加先减小后增大。这主要是由于，频率分断点较小时，超级电容器平抑功率过大，其容量配置过大，超级电容器成本投资过大。随着频率分断点的增加，蓄电池容量配置增大，超级电容器的配置容量减小，超级电容器成本投资的下降速度高于蓄电池成本投资的增加速度，系统年均综合成本减小。当频率分断点大于最优分断点继续增加，蓄电池平抑功率波动性较大，频繁充放电降低其循环使用寿命，蓄电池投资增加，因而混合储能年综合成本增加。本文最优频率分断点为2.5 mHz，对应年均综合成本为1 406千万元，在此分断点下，超级电容器和蓄电池充放电功率如图6所示。

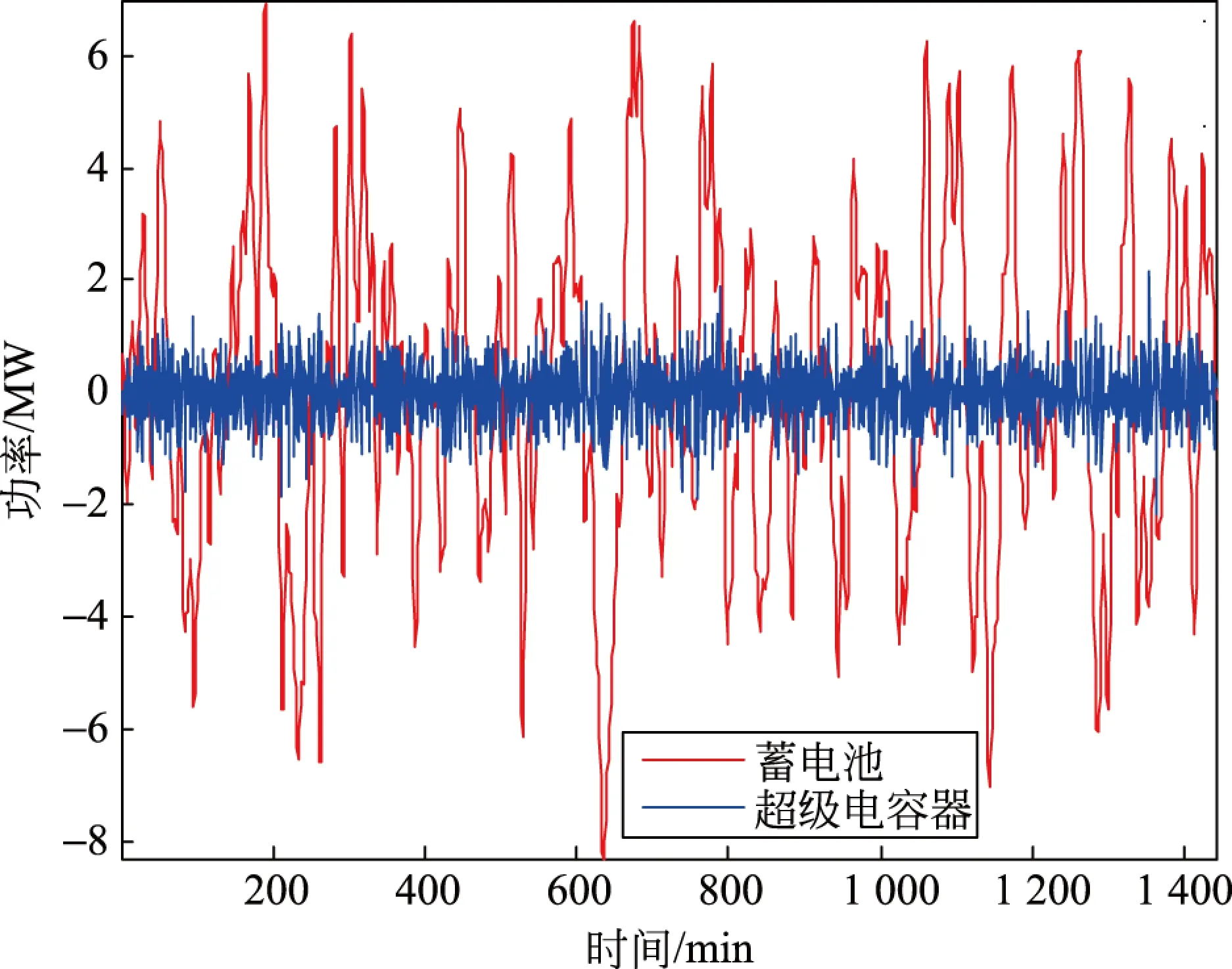
图6 功率分配曲线Fig.6 Curves of power distribution

由图6可以看出，超级电容器负责平抑波动幅值小，频率高的高频功率波动，降低了其容量配置；蓄电池负责平抑波动幅值大，频率低的低频功率波动，避免了频繁充放电对其寿命损耗的影响。

为了验证混合储能系统相对于单一储能系统的经济优越性，本文设计2组比较方案，方案I为单一蓄电池储能，方案II为单一超级电容器储能。比较结果如表4所示。

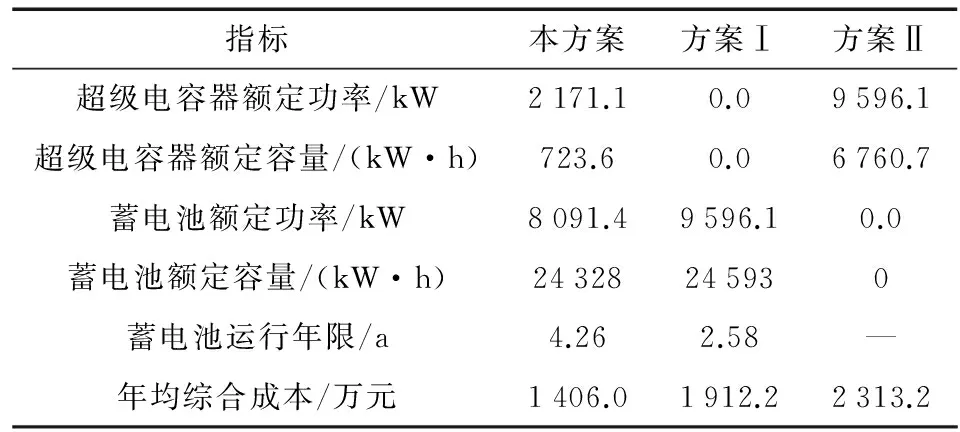
表4 储能系统配置结果

由表4可以看出，相较于方案Ⅱ，方案Ⅰ年均综合成本降低了17.34%，尽管方案Ⅰ中蓄电池容量配置高于方案Ⅱ中超级电容器容量配置，但作为功率型储能设备的超级电容器容量成本系数远高于蓄电池容量成本系数，因而其年均综合成本投资高于蓄电池。相较于方案Ⅱ，本方案年均综合成本降低了26.47%，超级电容器平抑高频功率波动，蓄电池平抑低频功率波动，即避免了超级电容器容量配置过大，成本投资增大，又避免了蓄电池频繁充放电，寿命损耗增加。因而混合储能系统年均综合成本低于单一类型储能系统，且混合储能系统中蓄电池的使用寿命高于单一蓄电池储能系统。

6 结论

微电网中配置储能系统可有效平抑风电功率波动，提高风电资源渗透率，储能系统容量配置影响其成本投资及经济效益，因此本文在保证并网功率满足波动限制要求的前提下，优化混合储能系统容量配置。采用滑动平均法平滑风电输出功率，以并网功率波动限制要求为约束确定窗口长度值，保证并网功率满足波动限制要求。采用频谱分析的方法分解波动功率，以年均综合成本最小为目标函数确定超级电容器和蓄电池充放电功率，实现超级电容器和蓄电池的容量配置最优。最后，建立了考虑蓄电池寿命损耗的混合储能系统成本模型，通过某风电场历史数据验证本方案的可行性及经济优越性。

[1] 曹超, 马玉鑫, 常悦, 等. 基于经验模态分解和模糊机会约束的混合储能容量配置方法[J]. 分布式能源, 2016, 1(3): 43-48. CAO Chao, MA Yuxin, CHANG Yue, et al. Capacity allocation method of hybrid energy storage system based on empirical mode decomposition and fuzzy chance constrained programming[J]. Distributed Energy, 2016, 1(3): 43-48.

[2] 陈谦， 陈霄逸， 金宇清， 等. 基于混合储能的大型风电场优化控制[J]. 电力自动化设备， 2015， 35(4): 76-70. CHEN Qian， CHEN Xiaoyi， JIN Yuqing， et al. Optimal control of large-scale wind farm based on hybrid energy storage[J]. Electric Power Automation Equipment， 2015， 35(4): 76-70.

[3] 张蕴昕， 孙运全. 混合储能在风光互补微网中的控制策略[J]. 电力系统保护与控制， 2015， 43(21): 93-97. ZHANG Yunxin, SUN Yunquan. Control strategy of a hybrid energy storage in wind-solar hybrid generation micro-grid[J]. Power System Protection and Control， 2015， 43(21): 93-97.

[4] 刘世林， 文劲宇， 孙海顺. 适用于风电功率调控的复合储能系统及其控制策略[J]. 中国电机工程学报， 2015， 35(1): 95-101. LIU Shilin, WEN Jinyu, SUN Haishun. Hybrid energy storage system and its control strategies intended for wind power conditioning[J]. Proceedings of the CSEE， 2015， 35(1): 95-101.

[5] 程启明， 徐聪， 程尹曼， 等． 基于混合储能技术的光储式充电站直流微网系统协调控制[J]． 高电压技术， 2016， 42(7): 2073-2083． CHENG Qiming， XU Cong， CHENG Yinman， et al． Coordination control of PV charging station DC microgrid system based on hybrid energy storage technology[J]． High Voltage Engineering， 2016， 42(7): 2073-2083.

[6] 蒋平， 熊华川． 混合储能系统平抑风力发电输出功率波动控制方法设计[J]. 电力系统自动化， 2013， 37(1): 122-126. JIANG Ping， XIONG Huachuan. A control scheme design for smoothing wind power fluctuation with hybrid energy storage system[J]. Automation of Electric Power Systems， 2013， 37(1): 122-126.

[7] 刘方， 杨秀， 时珊珊， 等. 不同时间尺度下基于混合储能调度的微网能量优化[J]. 电网技术， 2014， 38(11): 3079-3087. LIU Fang, YANG Xiu, SHI Shanshan, et al. Hybrid energy storage scheduling based microgrid energy optimization under different time scales[J]. Power System Technology， 2014， 38(11): 3079-3087.

[8] 马速良， 马会萌， 蒋小平， 等. 基于Bloch球面的量子遗传算法的混合储能系统容量配置[J]. 中国电机工程学报， 2015， 35(3): 592-597. MA Suliang, MA Huimeng, JIANG Xiaoping, et al. Capacity configuration of the hybrid energy storage system based on Bloch spherical quantum genetic algorithm[J]. Proceedings of the CSEE， 2015， 35(3): 592-597.

[9] 孙承晨， 袁越， CHOI S S， 等. 基于经验模态分解和神经网络的微网混合储能容量优化配置[J]. 电力系统自动化， 2015， 39(8): 19-25. SUN Chengchen， YUAN Yue， CHOI S S， et al. Capacity optimization of hybrid energy storage system in micro-grid using empirical mode decomposition and neural network[J]. Automation of Electric Power Systems， 2015， 39(8)： 19-25.

[10] 孙纯军， 倪春花， 窦晓波. 基于SOC状态反馈的混合储能功率优化策略[J]. 电测与仪表， 2016， 53(15): 81-87. SUN Chunjun， NI Chunhua， DOU Xiaobo. Research on optimal power allocation strategy based on SOC state feedback in hybrid energy storage system[J]. Electrical Measurement & Instrumentation， 2016， 53(15): 81-87.

靳雯皓

(编辑 蒋毅恒)

Capacity Optimization Configuration of Hybrid Energy Storage System for Smoothing Wind Power Fluctuation

JIN Wenhao, LIU Jichun

(School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, Sichuan Province, China)

Wind power have the characteristic of generation output variability. To reduce the impact of power fluctuations on grids and improve the power quality of power system, this paper puts forward the capacity optimization configuration of hybrid energy storage system for smoothing wind power fluctuation. The paper adopts moving-average method to filter the fluctuation of power and smooth wind power. The window length of moving-average method will affect the smoothing effect of power and the capacity configuration of hybrid energy storage system, so we consider the fluctuation limit of grid power as constraints to determine the window length, then achieve its optimal choice. We use the method of spectrum analysis to decompose the fluctuation of wind power, and take the minimum annual comprehensive cost as the objective function to determine the compensation frequency bands of the super capacitor and the battery respectively, and then determine the charge and discharge power. Finally, we establish a cost model of hybrid energy storage system considering battery life loss, and verify the feasibility and economic superiority of the program through case analysis.

super capacitor; battery; hybrid energy storage system; life loss; moving-average method; spectrum analysis

TK 82

A

2096-2185(2017)02-0032-07

10.16513/j.cnki.10-1427/tk.2017.02.005

2017-03-09

靳雯皓(1992—)，男，硕士研究生，研究方向为混合储能系统优化控制， 351518893@qq.com；

刘继春(1975—)，男，博士，教授，研究方向为电力系统经济性分析及电力市场。