基于储能系统的风电场功率控制研究

冯 斐，任远洋，王德林

(西南交通大学电气工程学院，四川 成都 610031)

基于储能系统的风电场功率控制研究

冯 斐，任远洋，王德林

(西南交通大学电气工程学院，四川 成都 610031)

在分析储能系统的各物理模型的基础上，提出一种由数据流构建的适用于系统机电暂态计算的通用储能模型。通过调节储能系统充放电速率限制、储能容量等特性参数，模拟不同储能系统对平抑风电场输出功率波动的效果。利用Matlab/Simulink环境，将储能模型与风电场模型进行结合，以New England 10机39节点标准系统为例进行仿真；为优化储能系统的性能，利用粒子群(particle swarm optimization，PSO)算法对储能模块中的PI控制器参数进行寻优。最后，仿真结果验证了通用储能模型的有效性，该模型可为电力系统有功功率的稳定传输和动态稳定控制提供一定参考。

通用储能系统；风电场；PSO智能算法；功率控制

0 引言

随着化石能源的逐渐枯竭，以风力发电为代表的新能源并网容量逐步提升[1-3]。但风能自身存在的随机性、间歇性会对当地电网造成冲击作用，以至于影响电网的电能质量。风力发电与储能系统的结合可有效地提供系统暂态稳定性[4]，储能系统作为抑制系统功率波动的措施已成为增强系统消纳新能源能力的重要技术手段[5]。

文献[6]研究了风光储能系统平滑控制原理，通过储能系统平滑控制，抑制风光输出总功率中的高频波动；文献[7]将阻尼转矩分析(damping torque analysis，DTA)方法扩展至包含储能元件的复杂多机系统，研究了储能元件阻尼转矩的产生、传递、分配及影响模态阻尼的机制，验证了储能系统整定方法的可行性；文献[8]研究了在线路传输容量有限的情况下，提出了基于负荷水平和风速情况的储能模糊控制策略，可更好地提升系统的可靠性。文献[9]提出了基于统一控制策略的串并联型超级电容器储能系统改善并网风电场输出稳定性方法，证明了该储能系统能够在大风速扰动下平滑风电场的功率输出，降低风电场对电网的冲击。文献[10]建立了自回归滑动平均风速预测模型，并结合储能装置在电力系统中的应用情况，采用序贯蒙特卡罗仿真方法分析评估了风电场、储能装置及燃气轮机备用容量对发输电系统可靠性的影响。上述论文通过不同策略研究了储能系统对抑制风电并网功率波动的有效性；但上述文献大多基于特定的储能系统，针对性较强。

为研究不同储能系统对电磁暂态的影响，本文提出一种以数据流形式构建的适用于系统机电暂态计算的通用储能模型。为优化储能模型中PI控制器的效果，采用粒子群(particle swarm optimization，PSO)算法来调节PI控制器的比例和积分参数。将该储能模型与风电场模型结合，利用储能系统适时地吸收、释放能量，减少了风电场输出功率的波动量，显著提高了风电并网时系统频率的稳定性。

1 通用储能系统模型

1.1 储能系统的数学模型

作为平抑新能源功率波动的重要手段，储能系统被得到广泛关注和应用。目前，储能技术按照能量转换的不同形式，可分为以下3类： 1)以抽水储能、飞轮储能和压缩空气储能为代表的机械储能；2)以超导磁储能和超级电容储能为代表的电磁储能；3)以铅酸蓄电池、全钒液流电池和钠硫电池为代表的化学储能。

但是这些特定储能系统之间的区别主要体现在储能响应时延、充放电速率限制和储能容量限制方面特性参数存在不同，而这些特性参数在模型中通常以约束条件存在，其数学模型可以统一。

常见储能系统的结构均可归结为3个部分：储能元件部分、变流器部分及控制系统部分。而储能系统并网的端口特性与变流器的控制策略有很大关系[11]，变流器的控制策略一般分为外环控制和内环控制两个层次[12]。外环控制为有功控制。考虑在电力系统中，系统频率的波动主要受有功平衡的影响，故储能系统的有功出力采用频率控制的方法。以频率偏差信号Δω作为输入信号，经过PI控制器的控制，产生功率的给定值Pset，如图1所示。

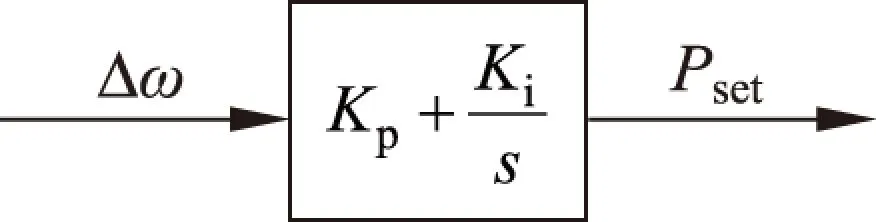
图1 外环控制框图Fig.1 Block diagram of outer control

内环控制采用有功解耦控制。文献[11]采用了前馈解耦策略和电流调节器采用PI调节的方法，得出了解耦后的电流控制方程，以此得出了电流控制方程的传递函数，借助相互抵消的原则，得出了储能装置注入系统的有功功率P的传递函数，其近似等效为1阶惯性环节：

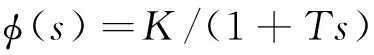
(1)

式中：T为时间常数；K为增益。

由式(1)可得出电流变换器交流侧产生的功率给定值Pset与储能装置注入系统有功功率P的特性方程：

(2)

储能系统的实时功率调节过程中，其内环功率控制过程可简化为1阶动态模型，如图2所示。

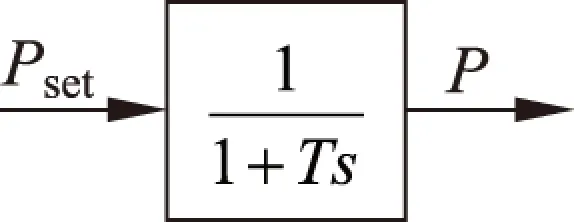
图2 内环等效控制框图限流环节Fig.2 Current restriction link of equivalent control block diagram of inner loop

考虑到储能系统容量决定了储能的造价，实际情况中，储能系统的造价昂贵，所以必须对储能系统的容量加以限制。对于储能系统，储能容量至下限时无法释放能量，至上限时无法吸收能量，即有

(3)

式中：Sl为储能容量的下限；Sh为储能容量的上限；ΔP为储能系统吸收或释放的容量，吸收为正，释放为负；Δt为功率采样点值间的时间间隔。

另外，不同储能系统的充放电功率是不同的。储能的充放电功率，体现了储能系统平抑风电功率波动的能力。所以，在系统仿真中，设置不同的充放电功率值，就能衡量不同储能系统的效果。

1.2 储能系统的Simulink模型

Matlab/Simulink是面向矩阵计算的科学计算软件，具有较强的数据处理能力[13]。因此，可以通过在Simulink中搭建储能系统的数学模型来研究平抑风电场功率波动特性。在Simulink中搭建的储能系统的数学模型分为2个模块：有功控制输出模块和能量限制环节。其中，有功控制输出模块如图3所示，能量限制环节如图4所示。

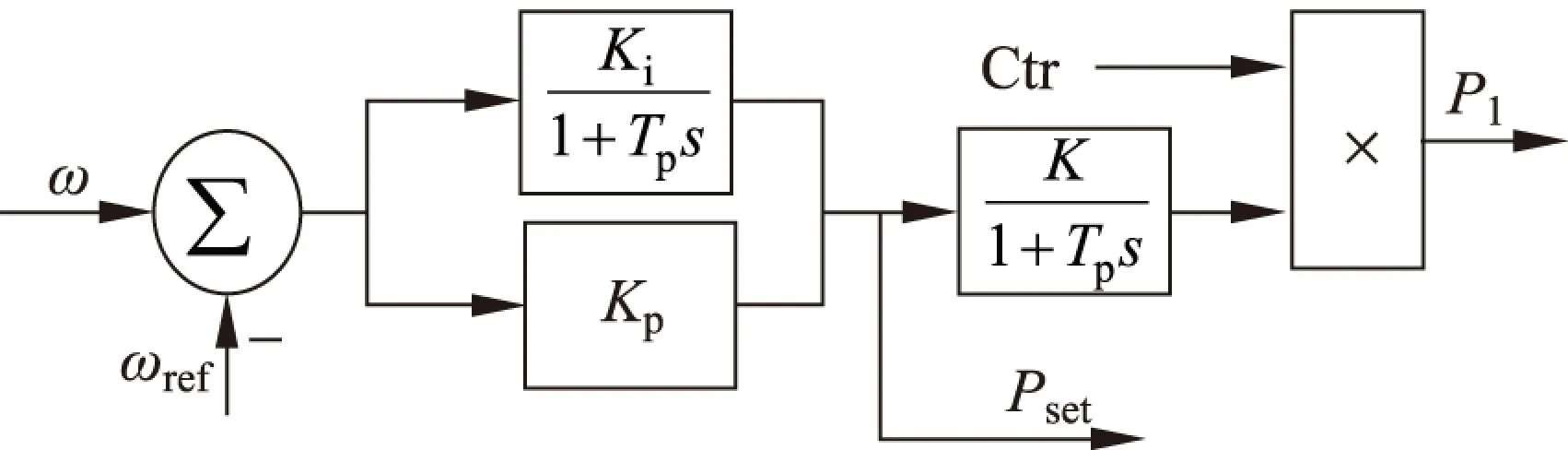
图3 有功功率输出模块Fig.3 Active power output module

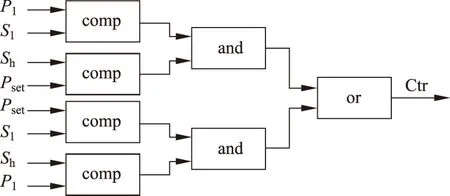
图4 能量限制环节Fig.4 Energy restriction link

图3、4中：ω表示风机的实际角频率，ωref表示风机的参考角频率，P1表示风机的实际输出功率，Pset表示风机有功功率的给定值，Ctr表示能量的控制信号，Sl表示储能容量的下限，Sh表示储能容量的上限。comp模块用于比较输入量之间的大小关系，and模块和or模块分别表示“与”门和“或”门。

2 PSO算法控制策略

PSO算法对复杂非线性问题具有较强的寻优能力[14-17]，粒子群算法与Simulink模型之间连接的桥梁是粒子(即PI控制器参数)和该粒子对应的适应值(即控制系统的性能指标)。优化过程如下：PSO算法产生粒子群，将该粒子群中的粒子依次赋值给PI控制器的参数Kp、Ki，然后运行控制系统的Simulink模型，得到该组参数对应的性能指标，该性能指标传递到PSO中作为该粒子的适应值，最后判断是否可退出算法[18]。更新粒子速度和位置采用如下方法：

(4)

(5)

式中：x为粒子的位置；v为粒子的速度；ω为惯性因子；c1、c2为加速常数；r1、r2为区间[0,1]的随机数；Pt为粒子迄今为止搜索到的最优位置；Gt为整个粒子群迄今为止搜索到的最优位置。

粒子群算法的实现步骤：

1) 初始化粒子群，随机产生所有粒子的位置和速度，并确定粒子的Pt和Gt。

2) 对每个粒子，将其适应值与该粒子所经历过的最优位置Pt的适应值进行比较，如较好，则将其作为当前的Pt。

3) 对每个粒子，将其适应值与整个粒子群所经历过的最优位置Gt的适应值进行比较，如较好，则将其作为当前的Gt。

4) 按式(4)、(5)更新粒子的速度和位置。

5) 如果没有满足终止条件(通常为预设的最大迭代次数和适应值下限值)，则返回步骤2)；否则，退出算法，得到最优解。

3 算例仿真

为验证本文提出的储能系统对风电场频率及功率的控制效果，本文选用图5所示New England 10机39节点电力系统，以风扰动为例对风电场的运行特性、各发电机母线电压相角及发电机节点的频率波动进行仿真分析。

图5 New England 10机39节点系统接线图Fig.5 Wiring diagram of New England 10-machine 39-bus system

本文在New England 10机39节点系统中的30号母线处增加1台由风电场等效成的直驱式永磁同步风力发电机。模拟中采用风机的实际输出功率为1.5 MW，而整个风电场的额定容量为200 MW。等效同步风力发电机的内阻抗为j0.8 pu，即忽略发电机内电阻的影响。等效直驱式同步风力发电机的功率因数设为0.95。风力机的主要参数如表1所示[19]。

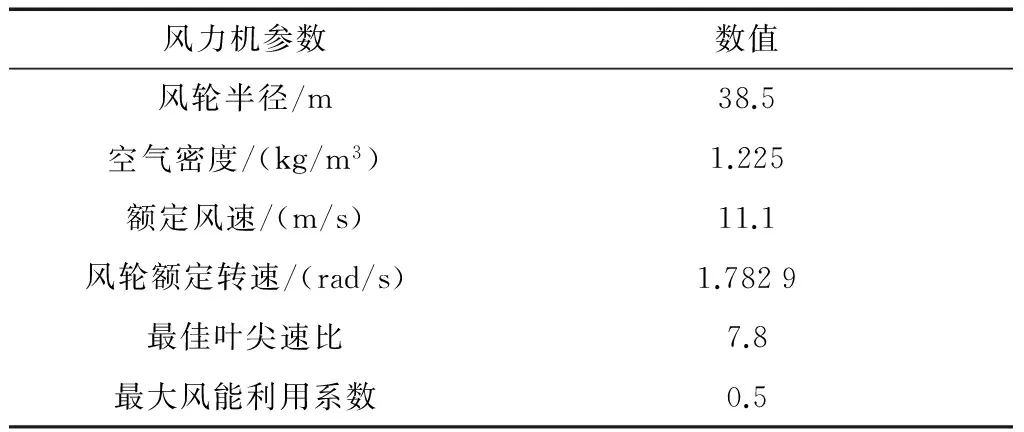
表1 风力机参数

本算例中空气动力学模型采用了详细的模型，为验证储能系统在风速时通过削峰填谷来快速稳定控制功率输出的效果，在t=0 s时刻，加入风速为11.1 m/s的基础风，并作用于整个仿真时间。为引起发电机输出功率的扰动，在t=2～4 s时，加入一个最大风速为3 m/s的阵风，风速变化曲线如图6所示。

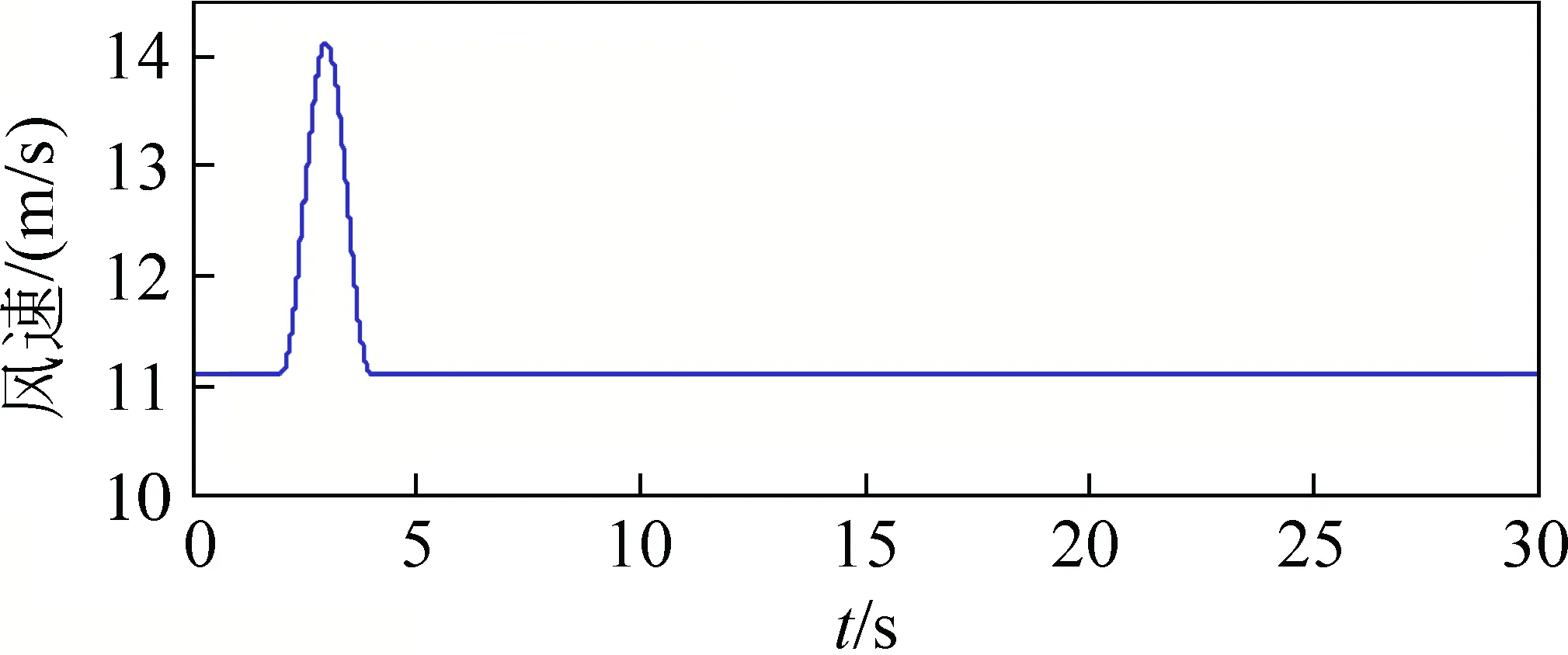
图6 风速变化曲线Fig.6 Curve of wind speed change

风速从额定风速状态转入阵风状态，输入功率随之出现波动，由图7、8可看出，系统频率在2 s时出现振荡，且恢复较为缓慢。加入储能模块之后，系统频率振荡有所下降，起到了抑制频率波动的效果。

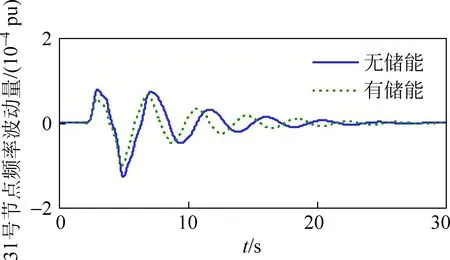
图7 常规机组频率波动情况Fig.7 Frequency fluctuations of conventional unit

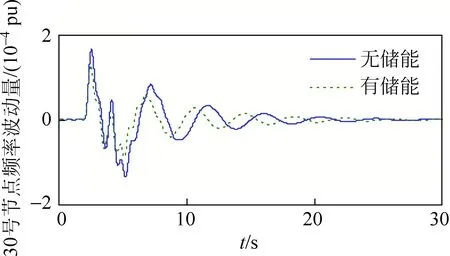
图8 风机机组频率波动情况Fig.8 Frequency fluctuations of wind turbine

本文在此种运行情况下加入储能系统，当不同容量储能系统加入后，对电网频率响应及相角增量差变化情况进行了对比，以验证模型的有效性。

由于节点数目较多，以28、30和31号节点分别代表非发电机节点、风机并网节点和普通发电机节点进行分析。风力机在上述扰动的情况下，加入不同充放电容量而其他特性参数相同的储能系统，对非发电机节点和发电机节点的相角增量差变化情况进行了对比，如图9—11所示，图中s表示储能系统的容量。

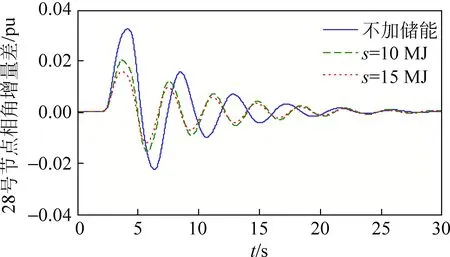
图9 非发电机节点相角增量差变化对比Fig.9 Comparison of incremental difference changes of phase angle of non-generator node

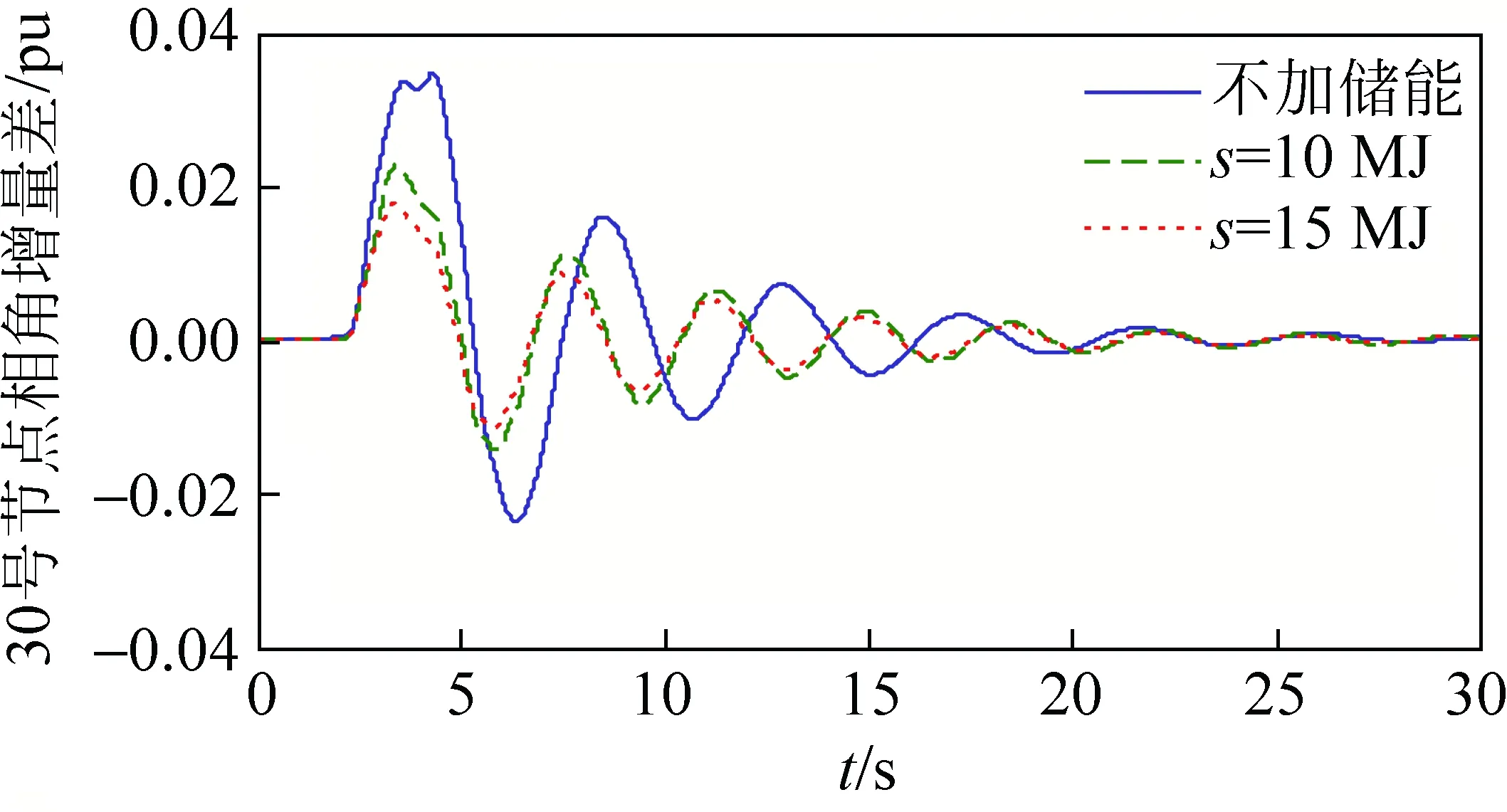
图10 风机节点相角增量差变化对比Fig.10 Comparison of incremental difference changes of phase angle of wind generator node

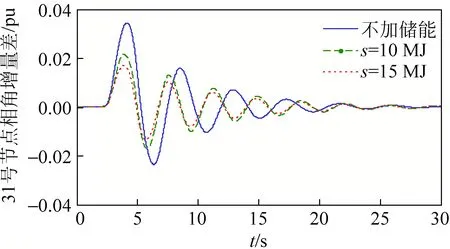
图11 发电机节点相角增量差变化对比Fig.11 Comparison of incremental difference changes of phase angle of generator node

从图9—11可看出：加入储能系统后能明显改善风电场输出功率波动的情况；不同储能系统对平抑风电场功率波动的能力也是不同的；随着储能系统容量的增加，输出功率的波动越小。

4 结论

本文提出了通用储能系统的数学模型，并将其与风电场结合，利用Simulink仿真分析了在添加储能装置的情况下，风电场输出功率和频率的变化情况。结果表明：

1) 利用PSO智能算法优化了的储能系统，能够较好地提供系统动态稳定控制；在平抑风电场输出功率波动方面，具有很好的效果。从而极大程度上解决了风力发电随机性、波动性的问题。

2) 添加了PSO智能算法的储能装置，可以推广利用到光伏发电等方面。在具体的工作环境中，PSO算法可提供最优的PI控制器的比例和积分参数，因此解决了由于传统上PI控制器参数难以整定而造成控制器失调的问题。

3) 从调节储能系统容量来仿真分析风电场的功率波动中可以看出，储能装置容量越大，对平抑风电场功率波动的效果越好。但从经济性和技术要求考虑，储能装置应该有一个最优容量，这是储能装置能否大规模应用的关键问题，也是极具意义的研究方向。

[1] LUNA-RUBIO R， TREJO-PEREA M， VARGAS-VAZQUEZ D， et al． Optimal sizing of renewable hybrids energy systems： a review of methodologies[J]． Solar Energy， 2012(86)： 1077-1088．

[2] ABBEY C， JOOS G． A stochastic optimization approach to rating of energy storage systems in wind-diesel isolated grids[J]． IEEE Transactions on Power Systems， 2009， 24(1)： 418-426．

[3] BAJPAI P， DASH V． Hybrid renewable energy systems for power generation in stand-alone applications: a review[J]． Renewable and Sustainable Energy Reviews， 2012， 16(5)： 2926-2939．

[4] BREKKEN T K A， YOKOCHI A， JOUANNE A V， et al． Optimal energy storage sizing and control for wind power applications[J]． IEEE Transactions on Sustainable Energy， 2011， 2(1)： 69-77．

[5] CONG T N． Progress in electrical energy storage system： A critical review[J]． Progress in Natural Science， 2009(3)： 291-312．

[6] 舒军． 风光储系统中储能单元的平滑控制方法研究[D]． 成都： 电子科技大学， 2012．

[7] 陈中， 杜文娟， 王海风， 等． 基于阻尼转矩分析法的储能系统抑制系统低频振荡[J]． 电力系统自动化， 2009， 33(12)： 8-11． CHEN Zhong， DU Wenjuan， WANG Haifeng， et al． Research on storage equipment to suppressing power system of low frequency oscillation with DTA algorithm[J]． Automation of Electric Power Systems， 2009， 33(12)： 8-11(in Chinese)．

[8] 汪新园． 大规模风电接入电力系统的可靠性评估及储能策略研究[D]． 杭州： 浙江大学，2013．

[9] 朱武， 操瑞发， 应彭华， 等． 超级电容器系统在改善并网风电场输出中的应用[J]． 电网技术， 2008， 32(S2)： 256-259． ZHU Wu， CAO Ruifa， YING Penghua， et al． Application of SCESS in improving stability of power system connected with wind farms[J]． Power System Technology， 2008， 32(S2)： 256-259(in Chinese)．

[10] 王剑， 刘天琪， 李兴源． 风电场及储能装置对发输电系统可靠性的影响[J]． 电网技术， 2011， 35(5)： 165-170． WANG Jian， LIU Tianqi， LI Xingyuan． Influences of connecting wind farms and energy storage devices to power grid on reliability of power generation and transmission system[J]． Power System Technology， 2011， 35(5)： 165-170(in Chinese)．

[11] 李妍， 荆盼盼， 王丽， 等． 通用储能系统数学模型及其PSASP建模研究[J]． 电网技术， 2012， 36(1)： 51-57． LI Yan， JING Panpan， WANG Li， et al． A mathematical model of versatile energy storage system and its modeling by power system analysis software package[J]． Power System Technology， 2012， 36(1)： 51-57(in Chinese)．

[12] 张崇巍， 张兴． PWM整流器及其控制[M]． 北京： 机械工程出版社， 2003．

[13] 于群， 曹娜． MATLAB/Simulink电力系统建模与仿真[M]． 北京： 机械工业出版社， 2011．

[14] ZIELINSKI K， WEITKEMPER P， LAUR R， et al． Optimization of power allocation for interference cancellation with particle swarm optimization[J]． IEEE Transactions on Evolutionary Computation， 2009， 13(1)： 128-150．

[15] PEDRASA M， SPOONER T D， MACGILL I F． Scheduling of demand side resources using binary particle swarm optimization[J]． IEEE Transactions on Power Systems， 2009， 24(3)： 1173-1181．

[16] 张智晟， 林涛． 电力系统经济负荷分配的量子粒子群算法[J]． 电工电能新技术， 2008(4)： 1-4， 13． ZHANG Zhisheng， LIN Tao． Research on power system of economic load dispatch with quantum-behaved particle swarm optimization algorithm[J]． Advanced Technology of Electrical Engineering and Energy， 2008(4)： 1-4， 13(in Chinese)．

[17] 于赞梅， 刘观起， 刘森． 基于双适应度微粒群优化算法的最优潮流计算[J]． 电气应用， 2007(4)： 25-29． YU Zanmei， LIU Guanqi， LIU Sen． Research on optimal power flow with double fitness particle swarm optimization algorithm[J]． Electrotechnical Application， 2007(4)： 25-29(in Chinese)．

[18] 史峰， 王辉， 郁磊， 等． MATLAB智能算法30个案例分析[M]． 北京： 北京航空航天大学出版社， 2011．[19] 周志超， 王成山， 郭力． 变速变桨距风电机组的全风速限功率优化控制[J]． 中国电机工程学报， 2015， 35(8)： 1837-1844． ZHOU Zhichao， WANG Chengshan， GUO Li． Output power curtailment control of variable-speed variable-pitch wind turbine generator at all wind speed regions[J]． Proceedings of the CSEE， 2015， 35(8)： 1837-1844(in Chinese)．

冯斐

(编辑 谷子)

Wind Farm Power Control Based on Energy Storage System

FENG Fei, REN Yuanyang, WANG Delin

(School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, Sichuan Province, China)

Based on the analysis of various physical models of energy storage system, this paper proposes a universal energy storage model constructed from the data stream which is suitable for system electromechanical transient calculations. By adjusting the charging/discharging rate limit of energy storage system, storage capacity and other characteristic parameters, we simulate the impact of different energy storage systems on stabilizing wind farm output power fluctuation. In Matlab/Simulink environment, the energy storage model is in conjunction with that of the wind farm. Next, the simulation is performed using New England 10-machine 39-bus standard system. In order to optimize the performance of energy storage systems, we adopt particle swarm optimization (PSO) intelligent algorithm to optimize the PI controller parameters in energy storage module. Finally, the simulation results verify the validity of the universal energy storage model, which can provide some valuable reference for the stable transmission of active power and dynamic stability control in power system.

universal energy storage system; wind farm; particle swarm optimization (PSO) intelligent algorithm; power control

TK 82

A

2096-2185(2017)02-0020-05

10.16513/j.cnki.10-1427/tk.2017.02.003

国家自然科学基金项目(51477143)

2017-01-05

冯斐(1993—)，男，学士，主要研究方向为电气工程及其自动化，fengfeiduan@foxmail.com；

任远洋(1994—)，男，学士，主要研究方向为电气工程及其自动化，632913981@qq.com；

王德林(1970—)，男，博士，副教授，研究方向为电力系统连续体建模、机电动态、频率稳定控制和风力发电等，dlwang@swjtu.cn。

Project Supported by National Natural Science Foundation of China(51477143)