换挡频次对离合器平均温升影响的研究∗

马 彪，陈 飞，李和言，王宇森，李明阳，李慧珠

(1.北京理工大学机械与车辆学院，北京 100081； 2.北京电动车辆协同创新中心，北京 100081)

换挡频次对离合器平均温升影响的研究∗

马 彪1，2，陈 飞1，李和言1，2，王宇森1，李明阳1，李慧珠1

(1.北京理工大学机械与车辆学院，北京 100081； 2.北京电动车辆协同创新中心，北京 100081)

考虑道路阻力系数建立履带车辆各挡位间换挡计算模型，分析了不同地区百公里直驶行程中各挡位换挡频次并进行道路试验验证。基于集总热阻网络理论改进换挡离合器液压系统平均温升模型，利用Simulink仿真，分析了换挡频次和冷却润滑油流量对离合器温升的影响。与台架试验对比表明：改进模型更接近试验结果，随着润滑油流量增加，温升速率减缓，对本文研究对象而言，单摩擦副润滑油流量以1.5～2L/min为宜；随着换挡频次增加，温度不断升高。通过对比分析平原、高原和湿热地区换挡频次对离合器温升的影响，拟合出温升与换挡频次的预测关系式：平原和高原地区3挡和4挡间的换挡频次最多，CL和CH离合器温升较高，湿热地区2挡和3挡间的换挡最为频繁，4个换挡离合器温升都高达82.9℃。

车辆工程；离合器；换挡频次；集总热阻网络

前言

换挡是实现车辆快速、经济行驶的重要操作，换挡的频繁程度体现了行驶工况的好坏程度，同时也决定了换挡离合器的热负荷状态。换挡频次无论对车辆机动性还是摩擦元件寿命都具有重要影响。

国内外对换挡过程中离合器热负荷及其动态特性进行了大量研究[1-4]。文献[5]中采用因子分析法对换挡过程中离合器的转矩和摩擦因数等进行了研究。文献[6]中基于变速器按各挡位使用频率加权，建立了传动系统热计算模型，对特定挡位的离合器温度场进行了数值计算。文献[7]中对履带车辆换挡工况瞬态动力学进行了分析。文献[8]中基于最小二乘支持向量机对离合器接合过程摩擦片表面温度进行预测并进行试验验证。

本文中针对高速履带车辆4个前进挡换挡状况建立换挡计算模型，在综合考虑道路阻力系数的同时，对不同地区挡位间换挡次数进行仿真与道路试验，同时改进了湿式离合器换挡过程平均温升模型，利用改进模型分析了不同地区换挡频次对离合器平均温升的影响并进行台架试验验证，拟合出温升与频次的预测关系式。

1 换挡频次统计分析

1.1 换挡理论模型

履带车辆换挡次数在很大程度上随使用地区和任务性质变化，道路阻力系数f作为换挡的主要评判因素必须加以考虑。定义换挡的顺序为系列，开始和结束排挡称为边界排挡，对换挡进行以下假设[9]：

①换挡只在相邻之间顺序进行；

②换挡是为了达到换挡系列的边界挡，在边界挡行驶的时间和路程远超过达到边界挡所需的时间和路程，即边界挡是长时间行驶的排挡；

③换挡过程均在以该系列的边界挡为特征的道路阻力数值下进行；

④换挡过程满足马尔科夫随机过程，即换挡随后的状况只取决于当前状况和它允许过渡到邻接状况的概率。

对于行驶100km的履带车辆，第i排挡自下而上转换次数可按下式确定[10]：

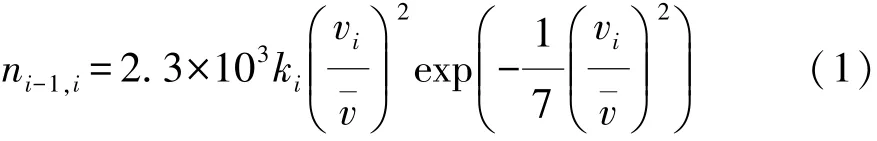
式中：ni-1，i为第i-1排挡换至i排挡的次数；vi为第i-1挡和第i重叠速度的平均值；v 为100km行驶平均速度；ki为随机换挡系数，可由式(2)确定，其中sj为第j挡的使用频率。

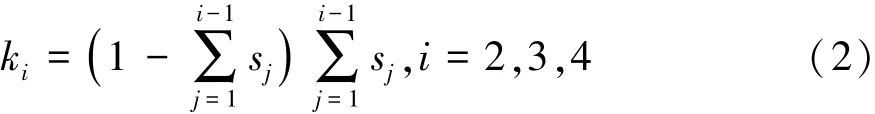
由假设①得ni-1，i＝ni，i-1，则相邻挡位换挡次数矩阵A为

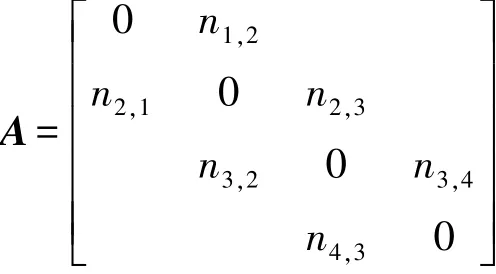
矩阵A第i行元素之和即为第i挡接合次数ni，将各挡换挡次数相加得到100km行程的换挡总数N，定义排挡接合的相对使用概率qi＝ni/N。对矩阵A按行正规化得到马尔科夫链的一步状态转移概率矩阵P，其中pij＝nij/(ni，i-1+ni，i+1)，j＝i±1。

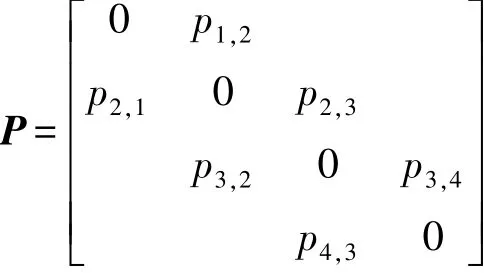
根据假设④，在建立换挡系列概率矩阵C时，需考虑当前和过渡状况的概率，如计算1挡换到3挡的概率时，需考虑以下概率事件：车辆长时间在1挡行驶概率q3；发生1挡换到2挡概率p1，2；发生2挡换到3挡概率p2，3；发生3挡换到2挡概率p3，2。之所以考虑最后一个事件是因为换挡结束的前提是系列方向发生改变。要发生1挡换到3挡这一概率事件就必须保证所列举的以上概率事件都发生，即c1，3＝q3p1，2p2，3p3，2。其一般形式为

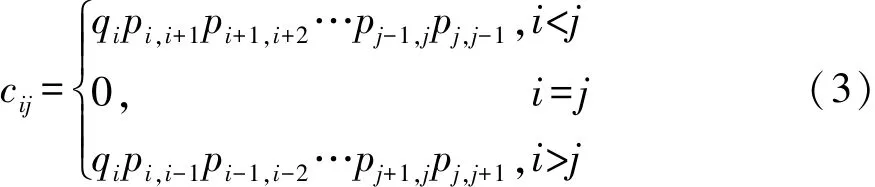
则换挡系列概率矩阵C可表示为

矩阵C元素具有以下含义：对角线以上和以下的第一个元素ci，i+1和ci，i-1是边界挡(长时间行驶排挡)接合的概率，其余元素ci，j(j≠i±1)表示从第i挡换到第j-1挡的概率(j为边界挡)；第i行的每个元素cij与第j挡行驶道路阻力系数fj相对应。

1.2 不同地区换挡分析

以平原地区计算为例，将初始参数道路阻力系数f、挡位使用比例s(见表1)和相邻挡位重叠速度v＝[14.28，23.7，39]km/h代入模型计算。

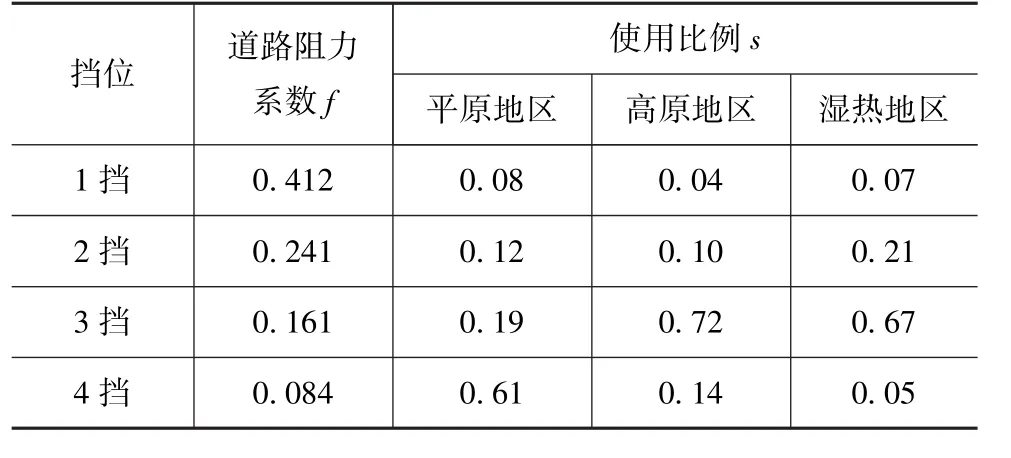
表1 不同地区挡位使用比例_

平原地区100km共计换挡N＝1210次，其换挡系列概率矩阵C为

将矩阵C乘以总换挡次数N即可得到100km行驶中各挡之间的换挡次数，如表2所示。

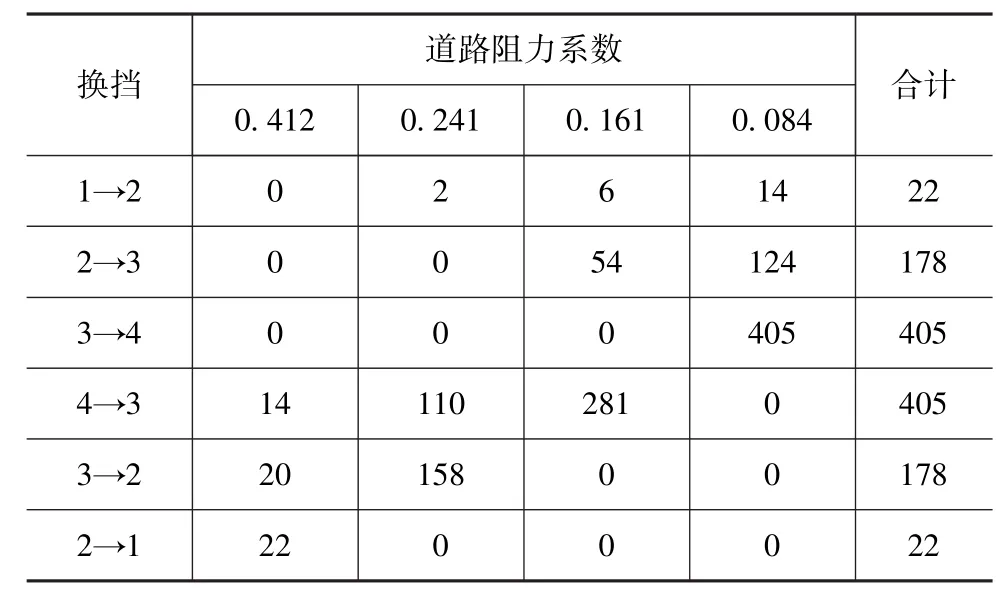
_表2 平原地区换挡计算(N＝1210)

表3和表4分别为高原和湿热地区各挡位之间换挡情况。对比表2～表4可知，高原地区无论在各挡之间还是总换挡次数均大于其他两个地区，且在3与4挡间转换次数最多；平原与湿热地区换挡次数相当，但湿热地区以2与3挡间转换为主，而平原地区以3与4挡间转换为主，这与挡位使用分配比例相对应。

1.3 道路试验对比

为验证计算模型的有效性，以某型履带车辆在北京(平原)、西藏(高原)、桂林(湿热)进行道路试验，平原地区路况最好，多为平坦公路和砂石路，以4挡行驶为主，高原地区虽然路况较好，但因缺氧造成发动机动力不足，以3挡行驶为主，湿热地区多为泥潭沟壑、陡坡等起伏道路，工况较为恶劣，以2和3挡行驶为主。试验中采用电子控制盒分别对两辆车的挡位进行监测，记录其挡位状态，其中1＃车分别在3个地区行驶472，1 509和1 042km，2＃车行驶250，1 597和1 030km，其不同地区平均100km换挡统计结果如表5所示。

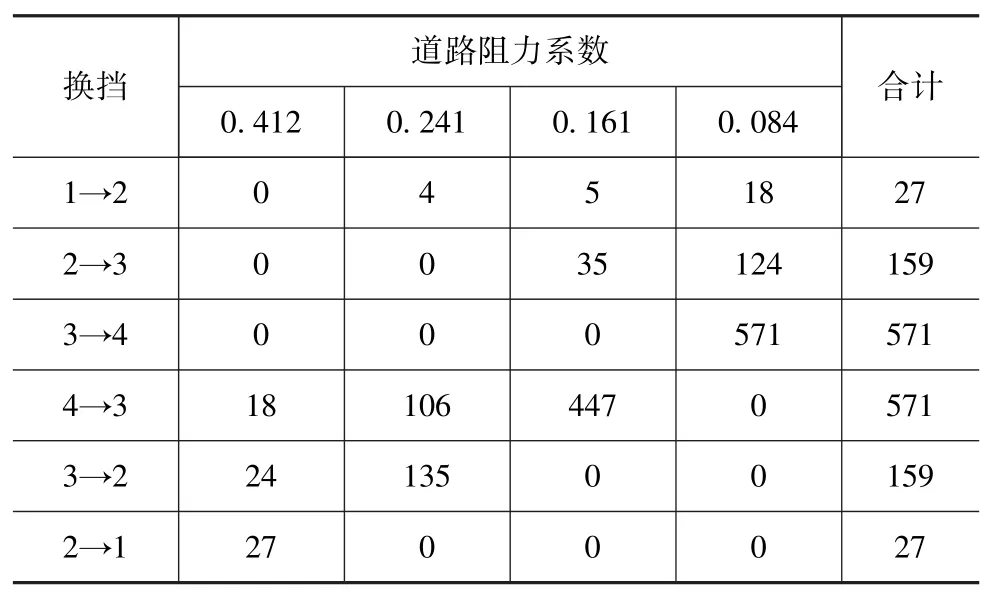
表3 高原地区换挡计算(N＝1514)

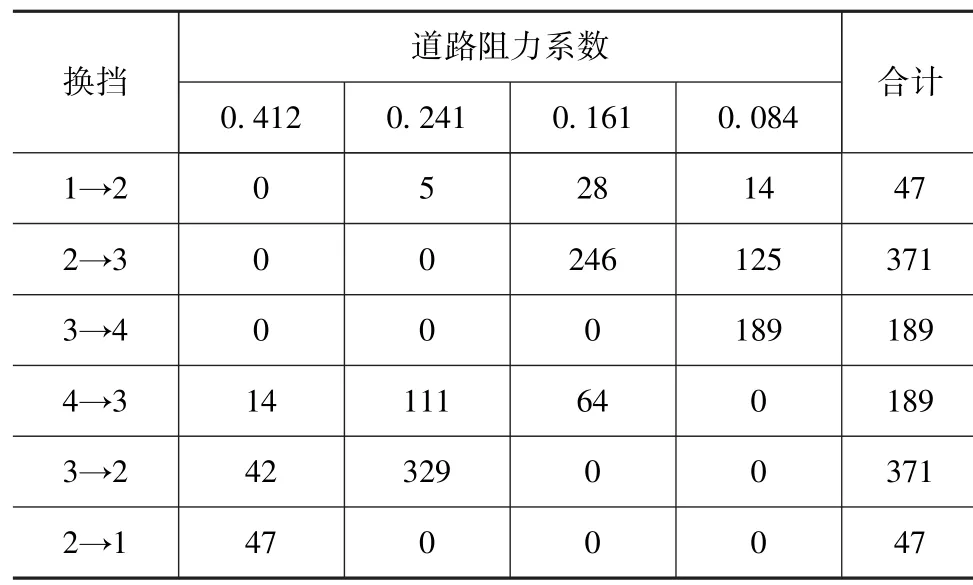
表4 湿热地区换挡计算(N＝1214)

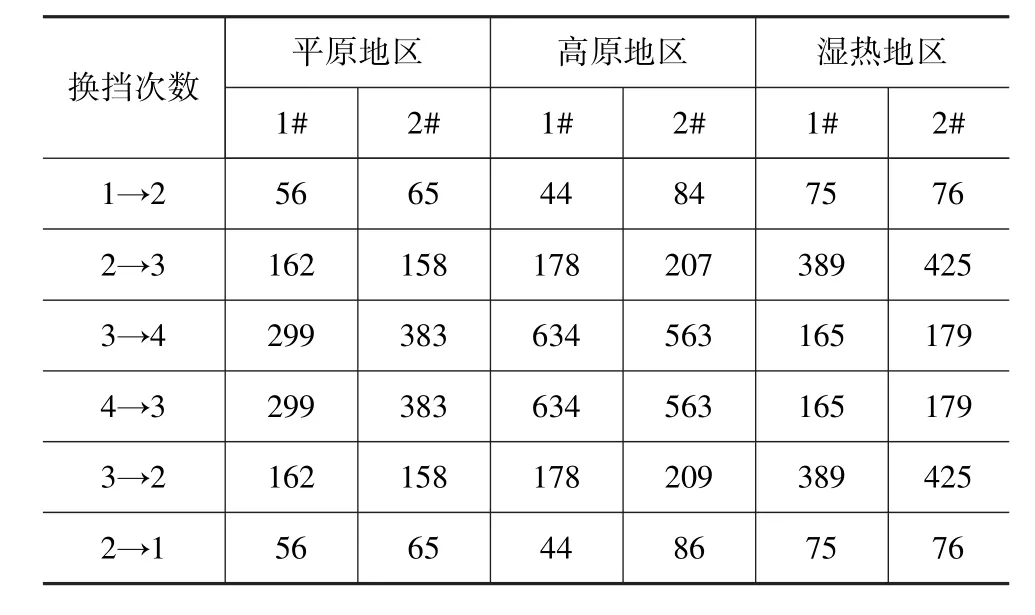
表5 100km不同地区换挡试验统计

图1为不同地区试验换挡统计与模型计算结果对比图。由表5和图1可知：

(1)两辆试验车在同地区同挡位间的换挡次数相当，这说明排除驾驶员因素外，换挡次数与道路阻力(工况)存在某种内在联系，且自下而上和自上而下换挡次数基本一致，验证了假设①的合理性；

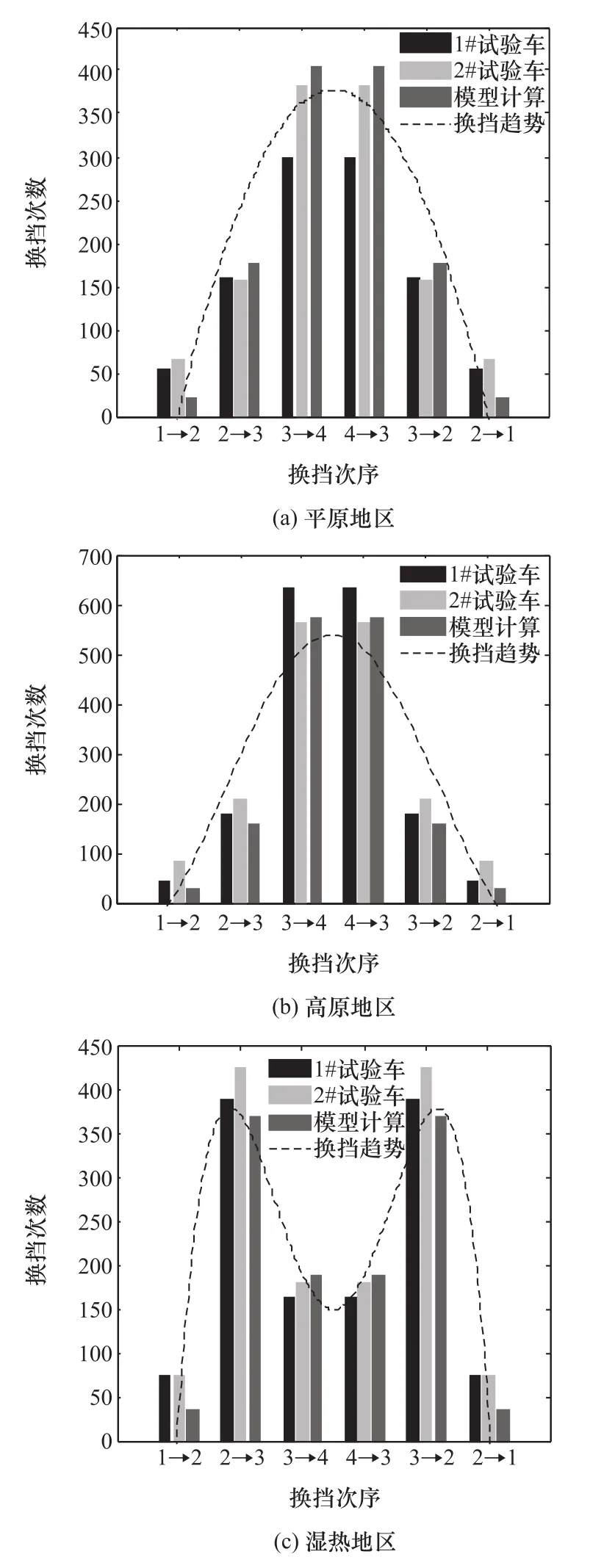
图1 不同地区间试验换挡统计与模型计算对比

(2)试验与模型计算结果变化趋势一致，平原和高原地区呈现高挡换挡多、低挡换挡少的总趋势，其中又以高原地区换挡次数最多，而湿热地区以中间挡换挡最为频繁，这与道路工况密切相关；

(3)试验与模型计算结果在中高挡的换挡次数较为接近，其误差在2%～14%，属正常误差范围，而在1与2挡间的换挡则相差较大，最高为2＃车平原地区相差66.1%，主要是由于在模型中未考虑倒挡，而试验时偶尔使用倒挡，模型中边界挡的增大导致换挡趋势外移，引起低挡相差较大，但其绝对误差43并非最大值，只是由于换挡基数小而导致相对误差较大，因此换挡模型具有一定的有效性。

2 改进离合器温升模型

2.1 离合器液压系统

在传热过程中，如果导热热阻相比对流换热热阻很小，可忽略固体内部热阻，此时采用集总参数分析法。忽略材料差异，将离合器液压系统各元件简化为节点，节点包含元件和润滑油。单离合器液压系统如图2所示。

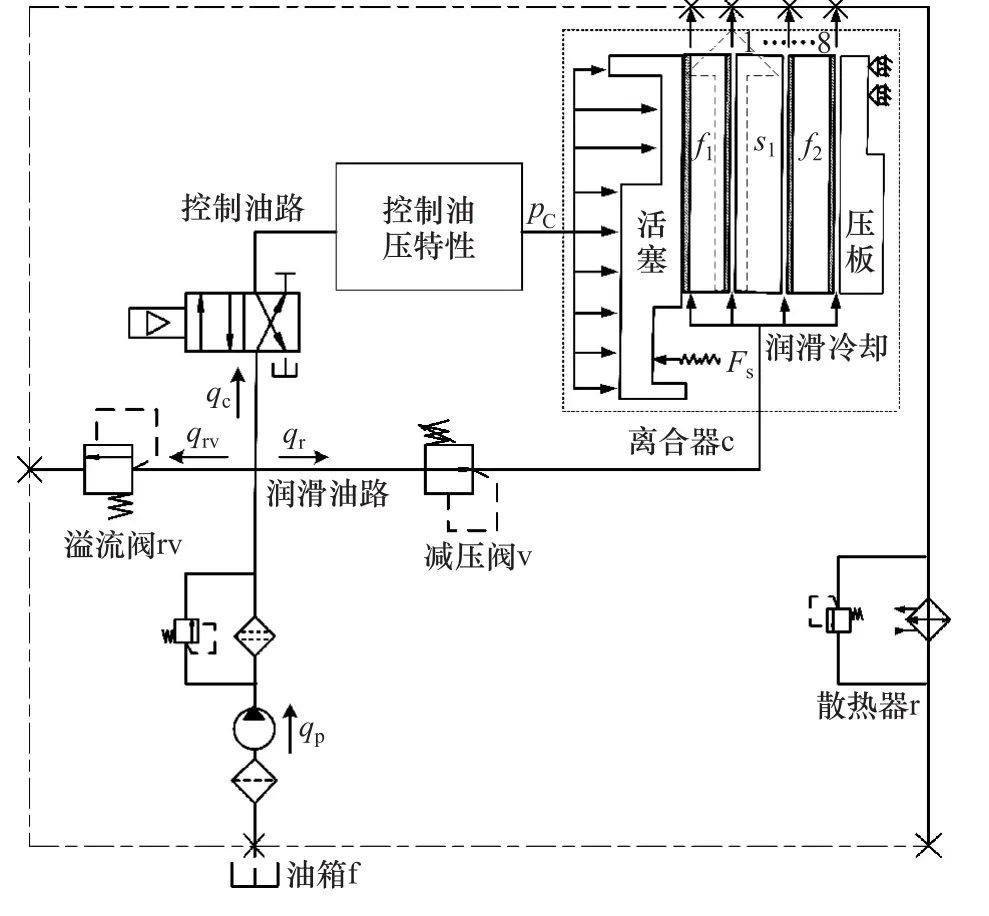
图2 离合器液压系统简图

对节点元件，导热方程为

式中：c为比热容；ρ为密度；λ为热导率；▽2为拉普拉斯算子；Φ·为热源在单位时间单位体积生成的热量。

对节点处润滑油，其导热方程为

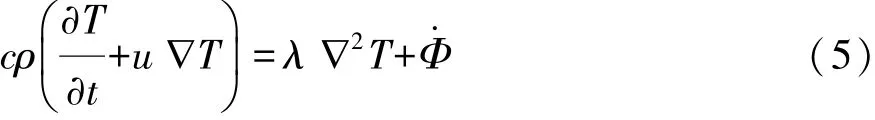
式中：u为流体流速；▽为梯度算子。

系统中离合器发热量远大于其它元件，基于集总参数的热阻理论对液压系统进行热平衡分析后发现，除离合器和散热器节点外，其余节点温升变化并不大[11]，因此将系统进行修正改进，改进后的热阻网络和离合器节点换热如图3所示。

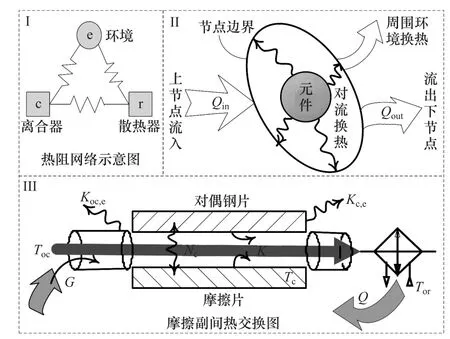
图3 离合器节点热阻换热图

对式(4)和式(5)求解可得到离合器和散热器节点元件及其内部油的热工况计算方程，其简化改进后的单离合器液压系统热状态方程为

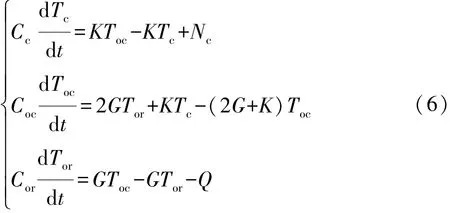
式中：Cc为离合器集总热容，Cc＝mccc；Coc为离合器冷却油集总热容，Coc＝mocco；Cor为散热器冷却油集总热容，Cor＝morco；K为离合器与冷却油换热系数，K＝hA；G为节点间冷却油换热系数，G＝ρqrco；Nc为离合器产热功率；Q为散热器散热能力。

离合器产热由主被动摩擦片速差和油压决定：

式中：μ为摩擦因数；r为摩擦副平均作用半径；z为摩擦副数；Ac为活塞承压面积；Fs为分离弹簧力；Δn为转速差。

散热器的散热能力为

式中：ε为散热效能，由传热单元系数NTU[12]确定。

2.2 仿真分析与试验对比

2.2.1 试验方法

为验证模型的可信性与准确性，搭建相应离合器测温试验平台，如图4所示。

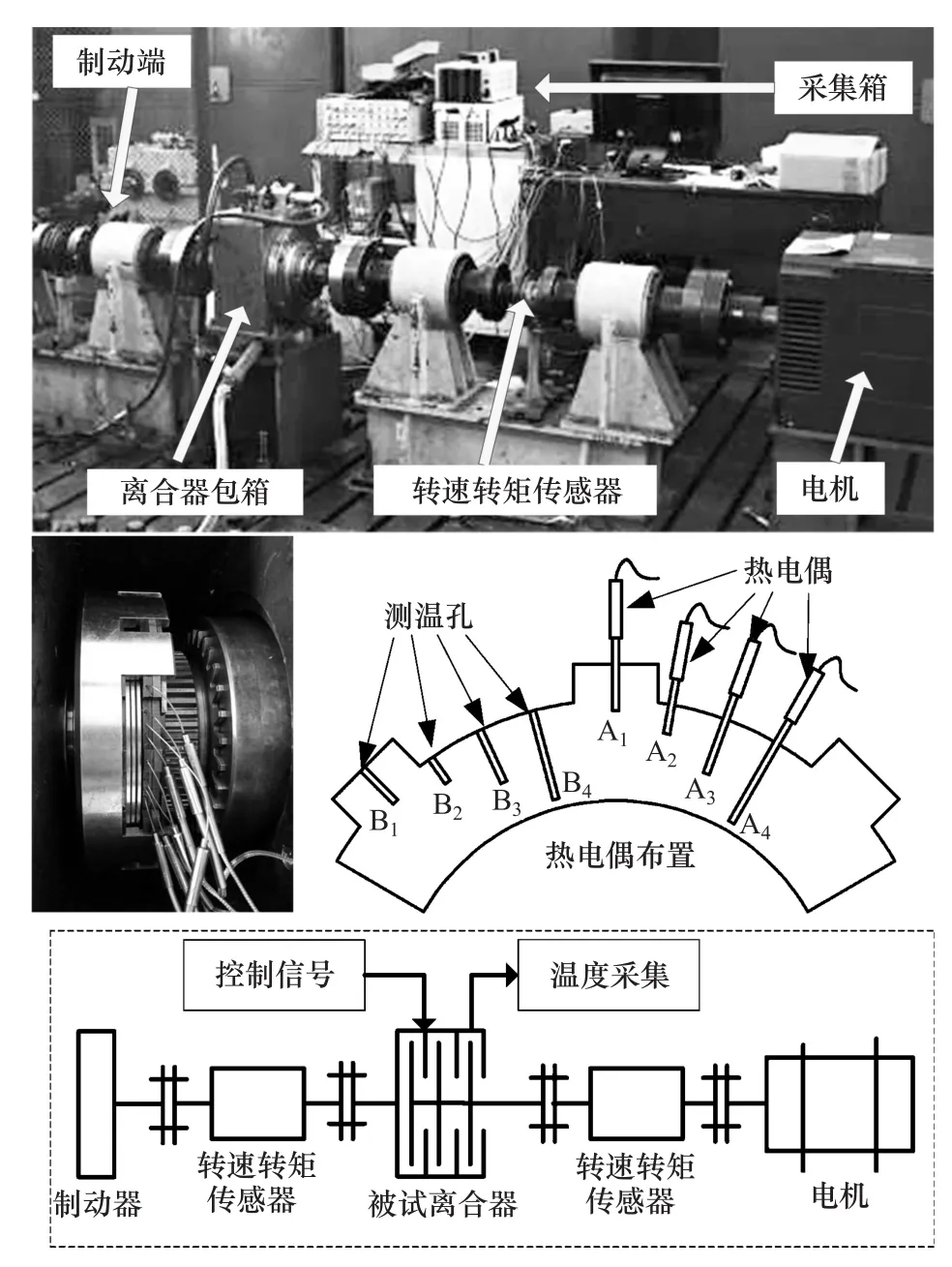
图4 离合器液压系统试验平台及摩擦元件测温方式

离合器被动端制动，主动端与电机相连，电机转速即主被动端转速差，通过电液比例阀控制离合器充油油压，实时监测温度和转矩变化，适时撤销接合压力并停机。为了更好地反映离合器整体温度，对摩擦元件采取图4所示沿不同径向和周向的测温方式，用A1～A4和B1～B4这8个点的平均温度表示离合器整体温度。

2.2.2 仿真对比分析

基于MATLAB/Simulink对改进离合器温升模型进行仿真计算，仿真条件设定为：恒压、恒转速差下低载长时滑摩工况，冷却润滑充分qr＝6L/min，有关参数如表6所示。

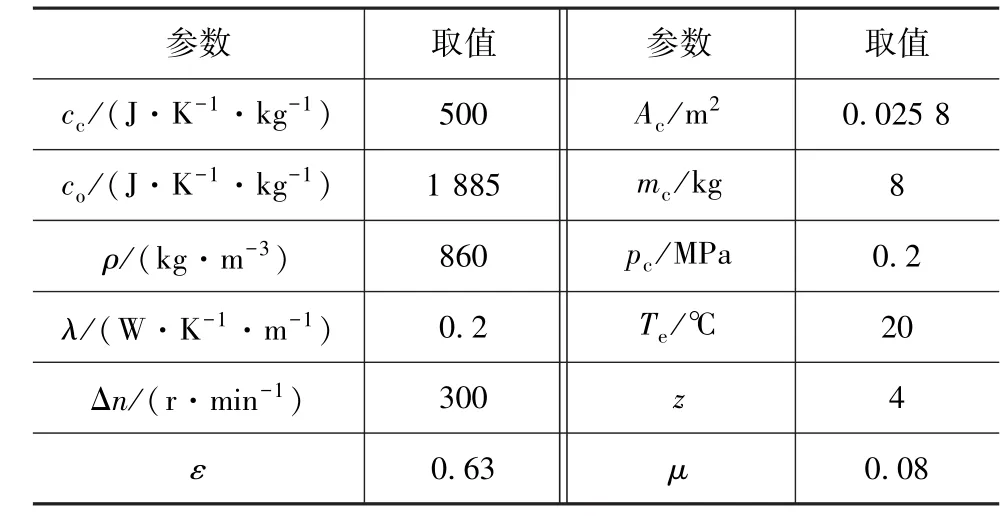
表6 仿真参数

图5为模型简化改进前后与试验结果对比曲线。由图可见，改进后离合器平均温升更加接近试验值，误差由原来的12.7%减小至8.2%，进而验证了改进离合器温升模型的可信性与准确性。

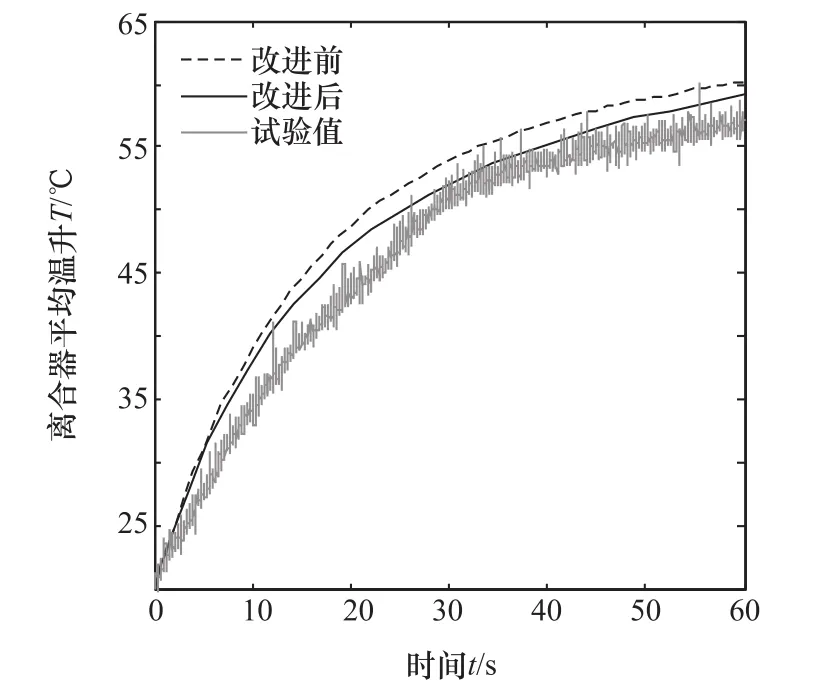
图5 改进模型温升对比

为探究不同滑摩频次n对单个离合器温升的影响，改变每分钟离合器滑摩接合次数，对不同滑摩频次的仿真值与试验结果进行对比分析，结果如图6所示。为覆盖离合器正常工作的热流密度范围，将工况设定如下：恒压为0.3MPa，恒转速差为400r/ min，每个周期内滑摩5s，而后进入全润滑冷却状态，直到下一个周期到来。

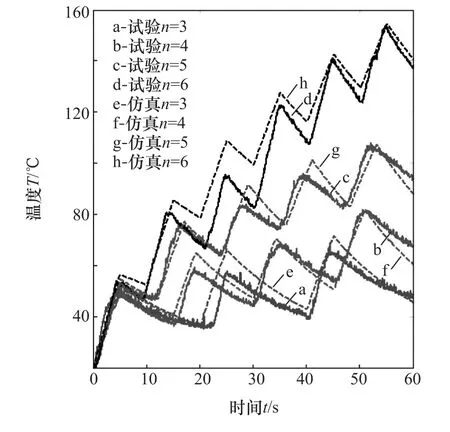
图6 不同滑摩频次下离合器温升对比

图6 显示4种不同频次下，仿真曲线与试验结果变化趋势一致，但仿真值在30s左右时比试验值大，两者随后逐渐持平，到达60s时仿真值低于试验值，这是由于随着温度的升高，液压系统在散热器冷却作用下逐渐进入热平衡阶段(如图5所示)，温升变缓，由式(8)知，随着冷热流体的温差增大，散热效果逐渐显著，导致在热平衡阶段的非滑摩时间内温降越发明显。由于试验操作中并非严格控制滑摩与非滑摩时间段，导致产生了一定的人为误差，但其误差为工程容许，模型能有效反映不同滑摩频次对离合器平均温升的影响规律。

冷却润滑流量对温升有重要影响，在滑摩频次为4的上述工况中，改变冷却润滑流量，进行仿真与试验对比分析，结果如图7所示。由图可见，仿真值与试验结果在初始阶段能很好吻合，随着温度不断升高，两者之间稍有远离趋势，且冷却润滑流量越小，远离趋势越明显(如曲线1与4温差比2与5大)，在进入热平衡阶段后，两者误差又逐渐减小。比较3种润滑流量知：qr越大，温升越小，润滑流量从2增加至4L/min时，温升减小23.7%，而从4增加至6L/min时，温升仅减小12.7%。研究发现，随着润滑流量增加温升速率变缓，这表明并非流量越大温降越明显，模型中取6～8L/min较为合适，对应单摩擦副流量取1.5～2L/min为宜。

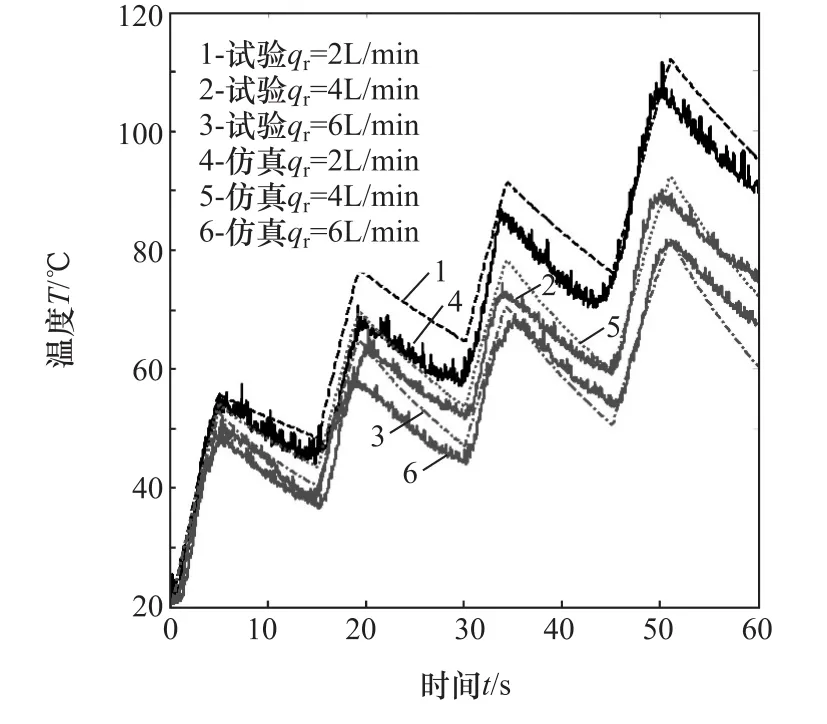
图7 不同冷却润滑流量下离合器温升对比

3 换挡频次对多离合器系统温升影响

某履带车辆综合传动装置的简图如图8所示。变速器由4个离合器组合接合实现4个前进挡，其换挡逻辑如表7所示，其中2与3挡之间转换需同时接合两个离合器，即存在两个离合器处于滑摩产热，其余挡位间转换仅有一个离合器处于滑摩产热。

以平原地区为例，分析换挡频次对多离合换挡操纵温升的影响。按平原地区换挡计算结果，单次循环换挡转换如表8所示。

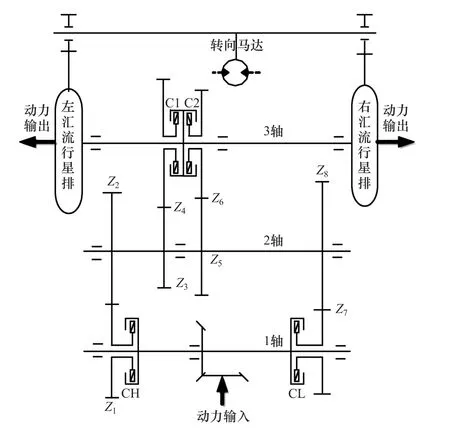
图8 某履带车辆综合传动装置简图

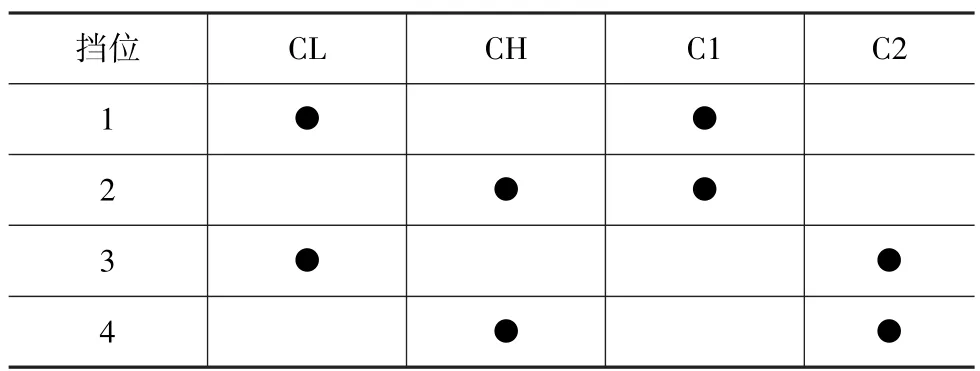
_表7 挡位逻辑

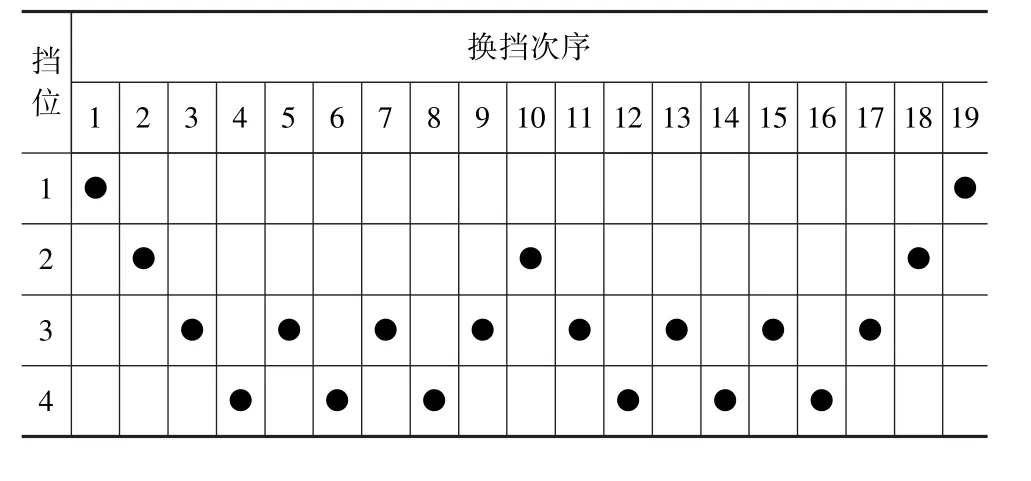
表8 平原地区换挡操纵次序

单次离合器输入条件如图9所示，油压采用试验中的缓冲油压，速差从1 400r/min在0.5s内降为零，此时离合器滑摩结束，而后进入储备升压阶段，直至下次离合器接合。

仿真结果如图10所示，离合器CL和CH温度呈现“锯齿型”不断上升，离合器C1和C2温升较小，这与各自的工作状态相关，单次循环换挡中，3和4挡转换频繁，CL和CH交替接合使用，而C1和C2长时间保持接合或分离。当CL(CH)每次接合时，温升约10℃，而后进入全润滑冷却状态，冷却速率随温度升高而增大，这是由于温差越大，冷却换热越明显。

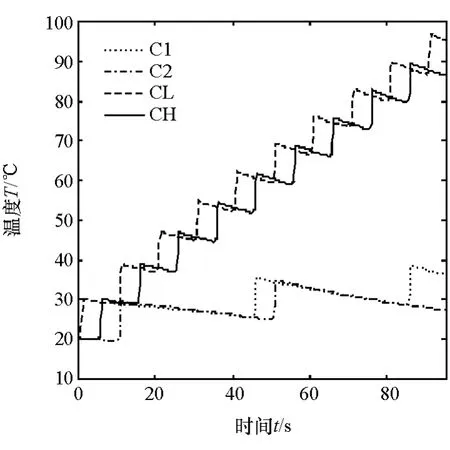
图10 离合器温升仿真结果

根据仿真结果，对离合器平均温升与冷却速率进行分析并拟合得到温升ΔT与换挡频次n关系：

ΔT＝9.78n+2.72n e-0.1n(9)

由摩擦材料的耐热性确定摩擦片的许用温升[ΔT]＜150℃，为保证离合器正常工作，计算知换挡频次n不宜超过14次。利用式(9)对3个地区离合器平均温升进行预测，平原地区CL和CH温升最高，ΔT＝76.9℃，而C1和C2温升较小，ΔT＝35.8℃；高原地区同样是CL和CH温升最高，ΔT＝97.9℃；湿热地区4个离合器温升都较高，ΔT＝82.9℃。这与各地区挡位使用次数相一致。

4 结论

本文中针对履带车辆挡位使用状况建立换挡系列模型，利用改进的离合器平均温升模型分析了换挡频次对温升的影响规律，结合道路和台架试验进行分析验证，针对研究对象得到如下结论：

(1)挡位使用频次与地区道路阻力系数密切相关，路面较好的地区，如平原和高原地区，驾驶员更倾向使用中高挡位，但工况的恶化会使中高挡换挡更加频繁；

(2)利用集总参数法简化离合器液压系统热阻网络，改进的温升模型更接近试验结果，随着冷却润滑流量增加，离合器温升降低，但降低速率减缓，单副润滑流量以1.5～2L/min为宜；

(3)分析对比各地区离合器温升仿真结果得到了温升与换挡频次的关系式，利用该式可进行离合器平均温升预测，高原地区3和4挡换挡频繁，CL和CH离合器平均温升最高达97.9℃，湿热地区2和3挡换挡频繁，CL，CH，C1和C2温升都高达82.9℃，为保证离合器可靠工作，换挡频次不宜超过14次。

[1] ZAGRODZKIP.Numerical analysis of temperature fields and thermal stresses in the friction discs of a multidisc wet clutch[J]. Wear，1985，101(3)：255-271.

[2] ZHAO J，MA B，LIH，et al.The effect of lubrication film thickness on the thermoelastic instability under fluid lubricating condition[J].Wear，2013，303：146-153.

[3] WALKER P，ZHANG N.Modelling of dual clutch transmission equipped powertrains for shift transient simulations[J].Mechanism and Machine Theory，2013，60：47-59.

[4] PISATURO M，SENATORE A.Simulation of engagement control in automotive dry-clutch and temperature field analysis through finite elementmodel[J].Applied Thermal Engineering，2016，93：958-966.

[5] MANSOURIM，KHONSARIM，HOLGERSONM，etal.Application of analysisof variance towet clutch engagement[J].Journal of Engineering Tribology，2002，216(3)：117-125.

[6] 王敬，邵朋礼，魏来生，等.车辆传动系统热平衡计算与仿真研究[J].工程设计学报，2003，10(6)：315-320.

[7] 项昌乐，何韡，刘辉，等.履带车辆传动系统换挡工况瞬态动力学分析[J].农业机械学报，2016，47(4)：288-292.

[8] 胡宏伟，周晓军，李雄兵，等.基于最小二乘支持向量机的AMT离合器片表面温度预测[J].汽车工程，2008，30(4)：335-339.

[9] 沃尔科夫，巴依科夫.履带车辆的设计与计算[M].刘太来，译.北京：北京理工大学出版社，1972：108-112.

[10] 安东诺夫.军用履带车辆传动装置[M].王红岩，译.北京：国防工业出版社，2014：184-191.

[11] 马彪，陈飞，李和言，等.湿式离合器摩擦副平均温升特性研究[J].兵工学报，2016，37(6)：961-968.

[12] GAOW Z，LIU JH，CHENG Y P，etal.Experimental investigation on the heatandmass transfer between air and liquid desiccant in a cross-flow dehumidifier[J].Renewable Energy，2012，37 (1)：117-123.

A Study on the Effects of Shifting Frequency upon Average Temperature Rise of Clutches

M a Biao1，2，Chen Fei1，Li Heyan1，2，W ang Yusen1，LiM ingyang1＆Li Huizhu1
1.School ofMechanical Engineering，Beijing Institute of Technology，Beijing 100081；2.Collaborative Innovation Center ofElectric Vehicle in Beijing，Beijing 100081

A model for calculating the frequency of gear shifting of a tracked vehicle is set up with consideration of road resistance coefficients，to analyze the shifting frequency with different gears in a hundred kilometer straight driving in different regions.An average temperature risemodel for the hydraulic system of shifting clutches ismodified based on lumped heat resistance network theory and a Simulink simulation is conducted to analyze the effects of shifting frequency and cooling lubricant flow rate on the temperature rise of clutches.The results of comparison between simulation and bench test show that the simulation results with modified model is closer to test ones，temperature rise rate reduceswith the increase of lubricant flow rate，and for the study object in this paper，the appropriate lubricant flow rate for single friction pair should be in the range of1.5～2L/min，and the temperature riseswhen shifting frequency increases.By comparatively analyzing the effects of shifting frequency on the temperature rise of clutches in plain，plateau and hot-humid regions，a predicted relationship between temperature rise and shifting frequency is fitted.In plain and plateau regions，the highest shifting frequency occurs between 3rd gear and 4th gear，withmore temperature rises in clutches CL and CH，while in hot-humid regions，the shifting between 2nd rear and 3rd gear ismost frequent，with the temperature rises in four shifting clutches all as high as up to 82.9℃.

vehicle engineering；clutch；shifting frequency；lumped heat resistance network

10.19562/j.chinasae.qcgc.2017.05.008

∗国家自然科学基金(51575042)和工信部基础产品创新科研项目(VTDP-3203)资助。

原稿收到日期为2016年6月1日，修改稿收到日期为2016年8月14日。

陈飞，硕士，E-mail：chenfei9342＠163.com。