环火星自主导航系统设计及参数优化研究

欧阳威，张洪波，郑伟

（国防科学技术大学 航天科学与工程学院，长沙 410073）

环火星自主导航系统设计及参数优化研究

欧阳威，张洪波，郑伟

（国防科学技术大学 航天科学与工程学院，长沙 410073）

当前火星探测器环绕段的导航信息主要依赖地面深空探测网提供，基于光学成像的导航方式尚不能提供较高的导航精度。因此提出一种应用相对测量的探测器实现火星环绕段的自主导航。两颗编队飞行的探测器进行相对测量，观测信息为探测器之间的相对视线矢量（LOS）。同时利用主星的星敏感器确定星体在惯性空间的姿态，将观测信息转换至惯性系下获得简化的观测方程，使用扩展卡尔曼滤波器（EKF）对卫星的轨道进行确定。介绍了具体导航方案的实现方法和技术细节，使用粒子群优化方法（PSO）对模型设计的相关参数进行优化，导航精度得到明显提高。实现位置确定精度10 m，速度确定精度0.01 m/s。为设计最优的编队导航系统参数提供了有效思路。

编队飞行；自主导航；扩展卡尔曼滤波；粒子群优化方法

0 引 言

目前已经成功实施的火星探测任务中，接近段和环绕段的导航信息主要由地面深空探测网（DSN）提供。然而由于地球和火星的距离较远，通信延迟使得探测器不能获得实时的导航信息[1]。美国2012年成功实施的“火星实验室”（MSL）任务中，通过密集的地面测量确定探测器的轨道参数并且精确地建立探测器的受力模型[2]。依靠地面站进行长时间跟踪测量的导航方式消耗了大量的资源。因此，发展火星自主导航技术对于降低导航系统的成本和实现探测器的自主探测尤为重要[3]。

当前，基于光学成像的导航技术已经应用到深空自主导航任务中，将导航相机拍摄的一系列照片通过非线性最小二乘滤波器估计得到探测器的位置和速度[3]。图像导航可以满足巡航段和接近段的导航精度，王大轶[4]等深入研究了深空探测任务中光学成像导航的技术难点，为我国将要开展的火星探测技术提供了技术储备。陈晓[5]等研究了使用天文导航的方法，通过观测太阳和行星视线矢量实现火星探测巡航段的自主导航。但是对于火星再入需要高精度的导航信息，基于视觉的自主导航方式难以满足。我国在2020年左右将要进行的火星探测任务中将实现对火星的环绕、降落和巡视，在没有类似美国深空探测网等地面探测设施支持情况下，发展深空自主导航技术是必要的。因此，本文利用编队卫星的相关技术，根据Psiaki[6]的研究成果，提出了一种使用编队飞行的探测器实现火星自主导航的方案。该方案使用双星编队的优良特性，确保两颗探测器能够长时间伴飞。将长时间的星间观测信息结合动力学系统，使用扩展卡尔曼滤波算法实现对探测器位置速度的估计。星载设备为Junkins[7]等人设计的相对测量视觉导航系统（Vision-based Navigation，VISNAV），通过星载激光雷达测量探测器之间的距离，使用星载相机获得相对方位角。获得探测器之间的相对测量信息后，结合主星的星敏感器测得其相对惯性系的姿态，就可以获得惯性系下的测量信息。

根据以上提出的自主导航方案，通过观测信息结合导航滤波算法可以达到较高的导航精度。但是系统设计的相关参数受具体任务限制，Yim[8]采取遍历的形式研究了不同的轨道根数对相对导航精度的影响。Ou[9]等研究了轨道根数对双星编队自主导航系统导航精度的影响。然而这些方法都只能够一次研究至多两个变量的变化对系统的导航性能的影响，实际上导航系统的设计是由轨道根数和编队构形因素共同决定的。已有研究表明，编队系统可观性主要由星间距离决定。因此，本文使用粒子群优化方法对主星的轨道根数进行全局优化。结果表明，优化后的参数可以明显提高系统的导航性能。

本文第1节给出了编队卫星自主导航系统的动力学模型和构形设计方法；第2节介绍了使用系统条件数度量系统可观测度的方法；第3节介绍了粒子群优化方法，并对导航系统设计参数进行优化；第4节使用扩展卡尔曼滤波算法对优化的结果通过数值仿真进行验证；第5节给出了结论。

1 双星编队导航方案

1.1 动力学模型和构形设计

考虑双星系统的动力学模型为

双星编队的构形设计采用文献[10]中基于相对运动运动学方程的设计方法，相对坐标系下简化的相对运动方程为

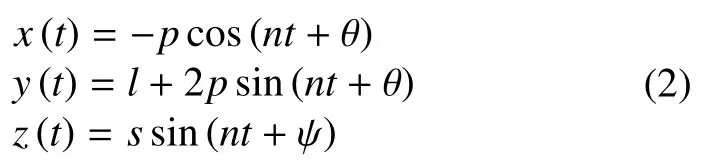
其中：p，s指定了相对运动沿径向、迹向和法向的三个分量；l确定了绕飞中心沿迹向的位置；相位参数θ确定了伴飞卫星在绕飞平面中的相位；Ψ确定垂直于绕飞平面的相位；这两个参数的差α和p，s共同确定相对运动轨道平面在惯性空间中的指向。具体的设计指标如表1所示，图1描述了探测器编队设计参数在相对运动坐标中的投影关系。

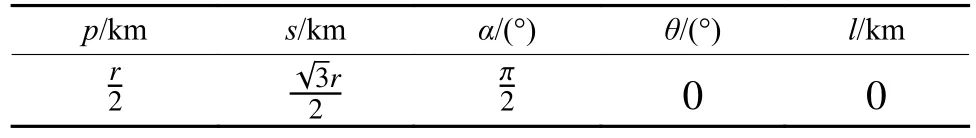
表1 编队构形设计参数Table 1 Formation configuration parameters

图1 编队设计参数示意图Fig.1 Configuration parameters of formation satellites

图2为主探测器和伴飞探测器围绕火星运行的示意图，OEXIYIZI为火星J2000.0惯性坐标系，oxyz为主探测器LVLH坐标系，r为视线矢量（LOS）。在实际任务中，从星可以是一颗重量较小、功能较简单的辅助性探测器，具备基本的辅助测量功能和轨道机动能力。

1.2 星间观测模型

本文根据Junkins等设计的VISNAV视觉导航模型，测量信息为伴飞探测器相对于主探测器的距离和方位。主星能够通过自身的星敏感器获得相对于惯性系的姿态，这样就可以把测量坐标系下的相对观测量转化为绝对观测量。本文为了分析的便利使用简化的观测模型避免非线性形式的观测方程，进一步避免滤波算法中对观测方程进行复杂的Jacobian矩阵求解[11]。在火星惯性系下简化的观测方程为

图2 编队运动示意图Fig.2 Trajectory of formation flying spacecraft

2 导航性能度量

2.1 系统可观测度分析

针对非线性动力学系统，理论上应该使用Lie导数构造可观测矩阵的方法进行可观性分析[12-13]。但是Lie导数的计算针对本文的动力学模型是非常复杂的，而且只能得到系统可观与不可观的结论。这里考虑到计算的便利，采用分段线性化的方法（PWCS）构造系统的可观测矩阵[14-15]，然后通过可观性矩阵的条件数来评价系统的可观测度。首先，需要将原始的连续非线性模型进行线性化，得到误差的动力学模型。

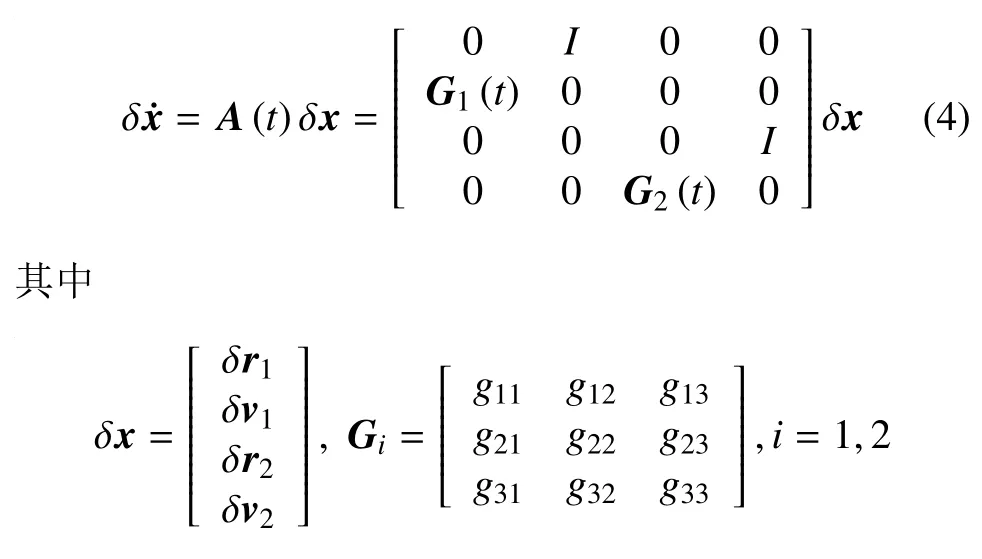
状态方程Jacobian矩阵中元素如下：

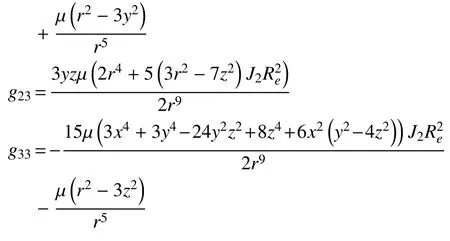
线性化后的观测方程为

系统可观测矩阵根据分段线性化思想构造如下：

其中：状态转移矩阵近似为

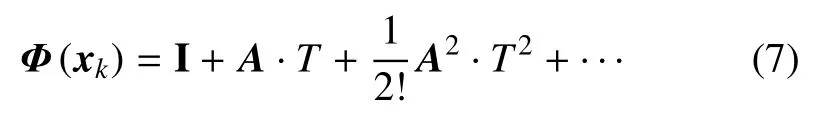
通过奇异值分解的方法计算可观性矩阵的条件数就可以判断系统的可观性。

2.2 参数优化目标的选取

在设计探测器编队的时候，需要确定的参数为主星的轨道根数和两颗探测器之间的距离。首先随意初始化主星的轨道根数和星间距离，构形为空间圆构形。获得的两颗探测器（SC）的初始轨道根数如表2所示。

表2 编队初始轨道根数Table 2 Nominal orbit elements of spacecraft formation

通过计算导航系统的条件数，获得导航过程中系统可观测度的变化趋势如图3所示。

图3说明每隔半个周期就会出现系统可观测度恶化的情况，这是由于从星在接近和穿越主探测器轨道平面的时候，观测信息不能反映出垂直于轨道面方向的状态变化的缘故[6,11]。为了让参数的选取可以使得系统的可观性最好，就需要寻找一个优化目标来评价系统的可观测度。由于系统条件数大小和系统可观度大小成反比关系，本文通过数值方法搜索一个周期内系统可观性矩阵条件数的最大值作为需要最小化的性能指标，实际上最大值出现的时刻就是从星穿越主星轨道平面的时刻。在设计导航方案的过程中，影响最终导航效果的参数包括：主星的轨道半径a，主星的轨道偏心率e，主星的轨道倾角i和编队卫星之间的距离r。然而导航系统参数的选择和任务的类型相关，上述参数需要在有限的范围内选取。本文主要考虑环火段的自主导航，系统的优化目标函数和参数的优化范围如下：

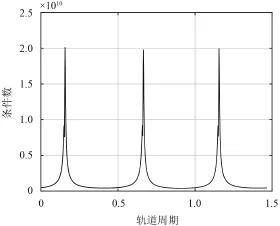
图3 系统条件数变化情况Fig.3 The condition number

至此，导航系统参数优化方案已经明确，接下来使用粒子群优化方法对参数进行优化，使得系统的导航性能最佳。

3 参数优化方案设计

对于经典非线性优化方法，大多采用梯度下降法求解，具有较强的局部搜索能力，但全局搜索能力较弱。粒子群优化算法作为一种群体智能优化算法，建立在同种生物之间信息的社会共享能够带来好处这一基础之上。粒子在飞行过程中考虑社会的经验，向邻域中其他粒子学习，使粒子在邻域中向所有粒子曾找到过的最好的点靠近[16]。本文结合两者的优点，首先采用粒子群优化算法进行全局搜索，然后使用非线性规划进行局部搜索，以获得问题的全局最优解。为了对比参数优化的效果，这里首先使用Matlab非线性规划函数fmincon对参数进行寻优，然后将得到的结果作为对比参照。该函数从一个预估值出发，搜索约束条件下非线性多元函数的最小值。表3给出20次非线性规划优化结果的平均值，图4显示了目标函数降低的过程。

表3 非线性规划优化结果Table 3 Nonlinear search optimization result

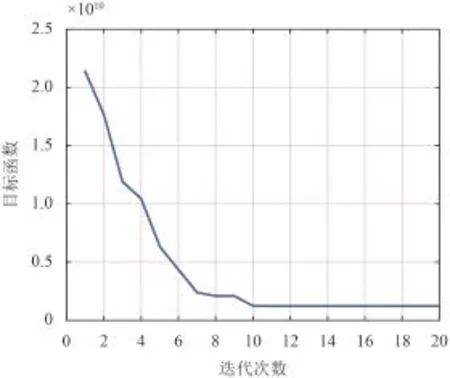
图4 非线性搜索目标函数的变化Fig.4 The condition number of nonlinear search

3.1 粒子群非线性搜索优化算法

粒子群优化算法中每个粒子都代表问题的一个潜在解，每个粒子对应一个由适应度函数决定的适应度值。粒子的速度决定了粒子移动的方向和距离，速度随其自身和其他粒子的移动经验进行调整，从而实现个体在解空间的寻优。利用非线性搜索（Nonlinear Search, NS）方法的局部搜索能力，在全局搜索的基础上进行局部搜索有助于提升粒子群优化算法的性能。算法执行框图如图5所示。

图5 粒子群非线性搜索算法流程图Fig.5 The PSO and nonlinear search（NS） method

粒子群优化算法的参数设置如表4所示。

表4 粒子群算法参数Table 4 PSO parameter set

使用以上参数进行优化，毎进化100代时使用非线性规划函数搜索局部最优值作为下一次进化的初始位置。优化结果对比如表5所示。

表5 粒子群算法优化结果对比Table 5 PSO optimization result comparison

目标函数下降过程对比如图6所示。

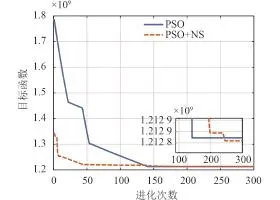
图6 PSO和PSO+NS优化情况对比Fig.6 The comparison between PSO and PSO+NS

可以看到，粒子群优化算法可以找到使目标函数全局最优的参数，使用非线性搜索方法进一步加强了局部搜索能力。同时，非线性搜索能够有效减少求解迭代次数，降低粒子群算法的时间复杂度。通过对比可以发现，当轨道高度越低，偏心率越大，星间距离越远的时候系统可观性越好，并且三种方法均能找到对应的最优参数。三者的区别在于轨道倾角，下面单独观察轨道倾角的变化对于可观测度的影响。图7使用表5中经过优化的参数仿真了不同轨道倾角下目标函数的变化。可以观察到目标函数在88°附近取得全局最小值，这一结果和通过粒子群非线性搜索优化得到的结果一致。

图7 轨道倾角对系统条件数的影响Fig.7 The condition number with various inclination

通过参数优化方法获得导航系统设计参数，可以看到优化后的参数是在约束范围内使主星的偏心率最大、星间距离最远、轨道高度最低、轨道倾角靠近88°。这一结果可能和探测器编队受到的摄动项的类型和编队构形相关。下面使用优化后的参数设计探测器编队，使用扩展卡尔曼滤波方法实现探测器的自主导航。

4 仿真分析

4.1 扩展卡尔曼滤波

由于系统的动力学模型是非线性的，考虑到计算的实时性，并且由于双星动力学系统的状态方程非线性程度不高，这里选用扩展卡尔曼滤波方法实现探测器状态的最优估计。

双星编队线性化后的系统误差方程为

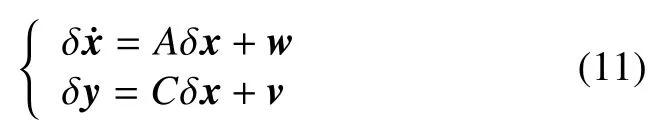
其中：A和C由式（4）和式（5）给出，w、v分别为系统过程噪声和观测噪声，其协方差满足

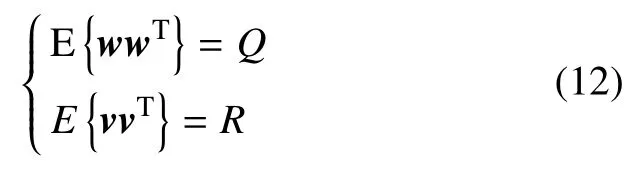
将上述线性化之后的动力学方程离散化后得到扩展卡尔曼滤波计算过程为

4.2 导航精度分析

根据以上的扩展卡尔曼滤波算法流程，进行导航滤波仿真，仿真步长为10 s，位置单位为km，速度单位为km/s。滤波器的相关参数设置如下。

过程噪声矩阵为

观测噪声矩阵为

状态初始协方差设置为

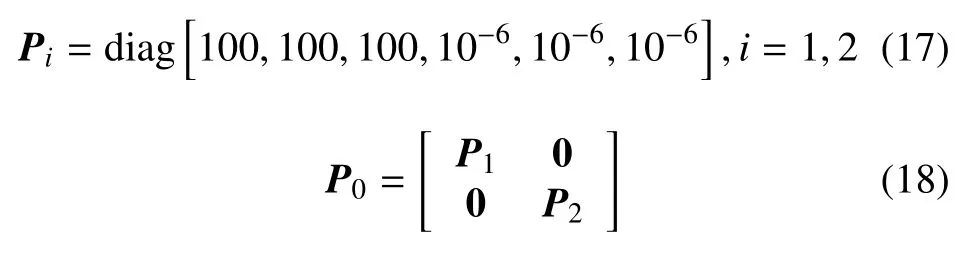
选用粒子群非线性搜索优化后的参数进行仿真分析。得到的位置和速度的估计结果如图8、9所示，探测器在火星惯性系下的运动轨道如图10所示。

图8 主探测器位置估计误差Fig.8 The position error of the chief

图9 主探测器速度估计误差Fig.9 The velocity error of the chief

图10 双探测器编队轨道确定结果Fig.10 The orbit of the formation

在最优参数设置的情况下，导航位置确定精度达到10 m，速度确定精度达到0.01 m/s。为了对比优化后的导航结果与任意设定的参数的差异，下面任取3组参数作为对照，如表6所示。

表6 粒子群算法优化结果对比Table 6 PSO optimization result comparison

采取50次Monte-Carlo仿真的方式对比3组参数导航精度的差异，对比的指标为整个导航滤波过程的位置误差均方根误差，定义为

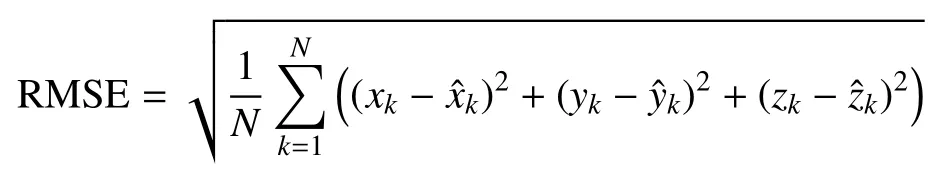
仿真对比结果如图11所示。

图11 Monte-Carlo对比结果Fig.11 Monte-Carlo simulation

Monte-Carlo仿真结果表明：通过粒子群非线性搜索优化算法寻找得到的参数进行导航系统设计，将获得更加高的位置确定精度。这也说明双探测器编队导航系统相关参数的优化选取对于导航的性能提升具有明显的作用。

5 结 论

本文提出一种使用双探测器编队进行火星环绕段自主导航的方案，该方案利用探测器之间的相对测量信息结合惯性姿态信息自主地确定探测器自身的位置和速度。需要注意的是，伴飞探测器只需要具备辅助测量的功能和简单的轨道机动能力，不需要复杂的系统设计，体积和重量都可以偏小。随后，结合粒子群算法的全局优化特性和非线性搜索方法的强局部搜索能力，优化设计编队的相关参数。优化结果表明，在约束范围内主探测器和从探测器之间的距离越远、轨道高度越低、轨道偏心率越大时系统具有越佳的可观测性能。在测量精度较高的前提下，通过扩展卡尔曼滤波算法对导航方案进行验证，滤波结果表明：在最优参数设置的情况下，位置估计精度可以达到10 m，速度估计精度可以达到0.01 m/s。Monte-Carlo仿真结果表明，使用优化后的导航系统参数进行导航将获得更高的导航精度。本文采用优化的方式寻找导航系统最优参数配置，为导航系统参数设计提供了思路。同时，也说明了轨道根数和编队构形参数对系统可观测性的影响。

[1]Schratz B C，Soriano M，Ilott P，et al.Telecommunica-tions performance during entry，descent，and landing of the Mars science laboratory [J].Journal of Spacecraft and Rockets，2014，51（4）：1237-1250.

[2]Martin-Mur T J，Kruizinga G L，Burkhart P D，et al.Mars science laboratory interplanetary navigation [J].Journal of Spacecraft and Rockets，2014，51（4）：1014-1028.

[3]于登云，孙泽洲，孟林智，等.火星探测发展历程与未来展望[J].深空探测学报，2016，3（2）：108-113.Yu D Y，Sun Z Z，Meng L Z，et al.The development process and prospects for Mars exploration [J].Journal of Deep Space Exploration，2016，3（2）：108-113.

[4]王大轶，黄翔宇.深空探测自主导航与控制技术综述[J].空间控制技术与应用，2009，35（3）：6-12.Wang D Y，Huang X Y.Survey of autonomous navigation and control for deep space exploration [J].Aerospace Control and Application，2009，35（3）：6-12.

[5]陈晓，尤伟，黄庆龙.火星探测巡航段天文自主导航方法研究[J].深空探测学报，2016，3（3）：214-218.Chen X，You W，Huang Q L.Research on celestial navigation for Mars missions during the interplanetary cruising [J].Journal of Deep Space Exploration，2016，3（3）：214-218.

[6]Psiaki M L.Absolute orbit and gravity determination using relative position measurements between two satellites [J].Journal of Guidance Control and Dy-namics，2011，34（5）：1285-1297.

[7]Junkins J L，Hughes D C，Wazni K P，et al.Vi-sion-based navigation for rendezvous，docking and proximity operations[C]// Proceedings of the annual AAS Rocky Mountain Guidance and Control Conference.Breckenridge，Colorado: AAS, 1999.

[8]Yim J R.Autonomous spacecraft orbit navigation [D].[s.l.]: Texas A&M University，2002.

[9]Ouyang W，Zhang H B，Xing J J.Autonomous orbit de-termination and observability analysis for formation satellites [C]// Chinese Control Conference.Chengdu，China：[s.n.]， 2016.

[10]Zeng G，Hu M，Yao H.Relative orbit estimation and formation keeping control of satellite formations in low Earth orbits[J].Acta Astronautica，2012，76（76）：164-175.

[11]Markley F L.Autonomous navigation using landmark and intersatellite data[C]// AIAA/AAS Astrodynamics Conference.Seattle，WA: AIAA, 1984: 1984-1987.

[12]常晓华，崔平远，王晓明，等.基于条件数的能观性度量方法及在自主导航系统中的应用[J].宇航学报，2010，31（5）：1331-1337.Chang X H，Cui P Y，Wang X M，et al.A condtition number-based observability analysis method and its application in autonomous navigation system.Journal of Astronautics，2010，31（5）：1331-1337.

[13]Yu Z S，Cui P Y，Zhu S Y.Observability-based beacon configuration optimization for Mars entry navigation[J].Journal of Guidance Control and Dynamics，2014，38（4）：643-650.

[14]Yu Z S，Cui P Y，Zhu S Y.On the observability of Mars entry navigation using radiometric measurements[J].Advances in Space Research，2014，54（8）：1513-1524.

[15]Chen T，Xu S.Double line-of-sight measuring relative navigation for spacecraft autonomous rendezvous [J].Acta Astronautica，2010，67（1-2）：122-134.

[16]杨维，李歧强.粒子群优化算法综述[J].中国工程科学，2004，6（5）：87-94.Yang W ，Li Q Q.Survey on particle swarm optimiza-tion algorithm[J].Engineering Science，2004，6（5）：87-94.

Study on Mars Autonomous Navigation System Design and the Parameter Optimization

OUYANG Wei，ZHANG Hongbo，ZHENG Wei
（College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China）

The navigation on Mars mainly depends on the assistance of the earth-based deep space exploration network，and the accuracy of optical imaging autonomous navigation technology is unsatisfactory.One method based on formation flying satellites（FFS）to autonomously determine the position and velocity is proposed in this paper.The measurement information includes the inter-satellite position and the absolute attitude.As the measurements are combined with the dynamics of formation satellites，the Extended Kalman filter（EKF）is used to optimally estimate the states.Relevant system parameters are optimized with intelligent optimization methods.The results show that the position accuracy can reach 10 m and the velocity accuracy can reach 0.01 m/s.

Mars autonomous navigation；formation flying satellites；Extended Kalman Filter（EKF）；intelligent optimization methods

V249

：A

：2095-7777（2017）01-0043-08

10.15982/j.issn.2095-7777.2017.01.007

欧阳威，张洪波，郑伟.环火星自主导航系统设计及参数优化研究[J].深空探测学报，2017，4（1）：43-50.

Reference format：Ouyang W，Zhang H B，Zheng W.Study on Mars autonomous navigation system design and the parameter optimization [J].Journal of Deep Space Exploration，2017，4（1）：43-50.

欧阳威（1992– ），男，硕士研究生。主要研究方向：深空探测自主导航，状态估计。

通信地址：湖南省长沙市开福区德雅路108号（410073）电话：15111031580 E-mail: ouyangweimissile@foxmail.com

[责任编辑：宋宏，英文审校：任树芳]

2016-11-01

2017-01-01

国家自然科学基金委重大项目（61690210）