基于引力场不对称性的三体系统轨道自主导航

王亚敏，刘银雪，蒋峻，孙煜坤，张永合

（1.上海微小卫星工程中心，上海 201203；2.中国科学院微小卫星重点实验室，上海 201203；3.北京理工大学 宇航学院，北京 100081）

基于引力场不对称性的三体系统轨道自主导航

王亚敏1,2，刘银雪3，蒋峻1,2，孙煜坤1,2，张永合1,2

（1.上海微小卫星工程中心，上海 201203；2.中国科学院微小卫星重点实验室，上海 201203；3.北京理工大学 宇航学院，北京 100081）

以月球背面的中继通信为背景，提出了基于三体系统引力场不对称特性的星–星测距自主定轨方案。该方案以环月极轨卫星和地–月L2点Halo轨道卫星组成中继通信网，以实现对月球两极和背面的覆盖。通过采集极轨卫星与Halo轨道卫星的测距信息，结合卡尔曼滤波在日–地–月动力学模型下获得两颗卫星的绝对轨道。数值仿真结果表明：本文方法能将导航的位置精度和速度精度分别提高到百米和厘米/秒量级。该自主导航方法还可以扩展到不规则引力场小天体附近星群运动的自主导航。

星间测距；自主导航；地–月三体；中继通信；深空探测

0 引 言

三体系统共线平动点由于其特殊的空间位置和低能量动力学特性，在天文观测、中继通信、低成本深空探测等领域有着广泛的应用。人类最早利用平动点始于20世纪70年代，Farquhar提出了将地–月L2点Halo轨道作为月球背面着陆器的中继通信卫星轨道的概念，并受到广泛关注[1-3]。自“Apollo 18号”的月球背面着陆探测任务中止以来，世界各航天大国提出了月球背面着陆的科学探测计划[4]，中国计划于2018年发射“嫦娥4号”探测器在月球背面艾肯盆地着陆并开展科学研究。月球背面的着陆探测不可避免地带来永久通信中断问题，因此，着陆器需要配备一颗中继通信卫星，以解决着陆探测器与地球的实时通信问题，而地–月L2点Halo轨道将是理想的中继通信卫星轨道[5]。

然而，地–月系统L2点的动力学不稳定特性要求L2点Halo轨道具有较高的定轨精度、控制精度，并执行频繁的轨道保持控制[6-7]，这对地面测控网将造成较大的压力。因此，三体系统平动点轨道的自主导航研究变得意义重大，不仅可以减轻地面站测定轨负担，还可以实现星上自主轨道维持及相应的任务自主规划，为实现星上的自主管理奠定基础。

为解决深空轨道的自主定轨确定问题，学者们提出了众多的天文导航方法，包括光学导航[8-11]、脉冲星导航等[12-13]。随着深空探测器小型化、分布式需求的提出，Psiaki等提出了采用星–星跟踪测距、测角定轨算法[14]，通过光学相机测量星间相对方位角以及相对距离信息，解算探测器的绝对位置。在缺乏星间相对方位角度信息的条件下，若仅依赖星间测距信息，只能解算轨道的形状与尺寸，而无法获得绝对指向，不具备解算探测器绝对轨道的能力。近年来，Hill等研究发现，对于三体系统、不规则小天体中的轨道运动而言，由于引力场的不对称性，探测器轨道的形状、尺寸对应唯一的轨道初值，星–星测距信息结合扩展卡尔曼滤波即可实现卫星绝对轨道的自主确定，同时，高精度自主定轨还可以提高目标天体的重力场模型精度[15-18]。高有涛等利用地–月三体系统平动点轨道与地球轨道卫星的测距信息设计了自主轨道确定算法，为地球轨道卫星的测距定轨提供了有益的思路[19]。

本文以月球背面和地球通信的中继通信卫星轨道自主导航为背景，开展了中继通信卫星轨道设计与基于三体系统引力场不对称特性的星间测距自主定轨算法研究。首先，利用地–月共线平动点轨道的低能量特性，通过近月点机动连接地–月转移轨道和Halo轨道稳定流形，实现地–月L2点Halo轨道之间的低能量转移。然后，通过状态转移矩阵建立日–地–月引力场下的卫星运动方程和观测方程，结合扩展卡尔曼滤波完成两颗中继卫星的自主导航。最后，以1 000 km高月球极轨和Az=8 000 km北族Halo轨道为例，通过仿真计算给出了轨道方案和自主导航结果，实现高精度自主导航。

1 地–月系统中继通信卫星轨道设计

本文兼顾到中继通信网对月球南北极区和月球背面的覆盖，以月球1 000 km高度极轨卫星sat1和L2点Az=8 000 km Halo轨道卫星sat1为例组建通信网，轨道构型如图1所示。鉴于环月轨道设计方法及工程实施已较为成熟，这里不再赘述，本节将重点对地–月L2点Halo轨道及其转移轨道的设计方法进行阐述。

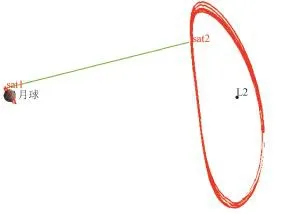
图1 月球背面自主导航系统示意图：月球极轨与L2点Halo轨道组网Fig.1 Illustration of auto-navigation on the far-side of Moon

1.1 仿真条件

在本文数值计算过程中，Halo轨道初值计算采用圆型限制性三体动力学模型，然后通过二级微分修正方法在日–地–月真实星历模型中获得精确数值解。数值积分工具为Runge-kutta78，积分过程所需的地球、月球、太阳位置与速度来源于DE405，引力采用质点引力模型，引力常数在本文中的取值分别为3.986× 105km3/s2、4.902 8×103km3/s2、1.327 12×1011km3/s2。本文的仿真计算不考虑太阳光压和行星非球形摄动。

1.2 地–月Halo轨道及其不变流形

Richardson三阶近似解析解提供了较为精确的Halo轨道解析解[20]，在圆型限制性三体模型中通过修正获得精确的初值。然而，在日–地–月系统中，圆型限制性三体系统所得到的Halo轨道初值将迅速发散，不能长时间绕飞在平动点附近。目前，针对真实星历模型中的Halo轨道设计问题，有两级微分修正和并行打靶算法[21-22]，将长周期的轨道分段联合修正。本文采用两级微分修正方法，Az=8 000 km北族HALo轨道的理想轨道与星历轨道如图2所示。

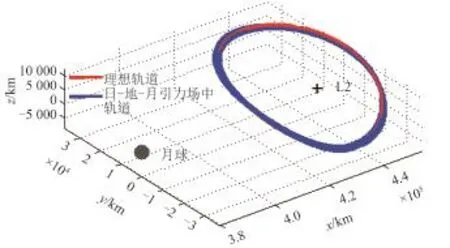
图2 圆型限制性三体系统Halo轨道及修正后的星历模型下Halo轨道Fig.2 Halo orbit in circular restricted three-body system and Sun-Earth-Moon ephemeris model

地–月L2点Halo轨道存在稳定、不稳定流形，运行于稳定流形的探测器可以随时间漂移进入目标Halo轨道，而运行于Halo轨道的探测器可以利用不稳定流形无须燃料消耗渐近远离，到达月球附近或远离地–月空间。Az=15 000 km、1 000 km及3 200 km的地–月L2点Halo轨道及其稳定流形如图3所示，稳定流形可以到达月球表面。利用这一零消耗转移特性，本文设计中继卫星从近月点进入Halo轨道的稳定流形，实现无燃料消耗的Halo轨道入轨。

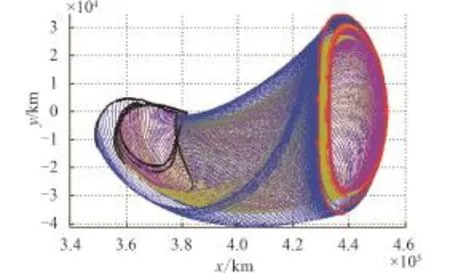
图3 地–月L2点Halo轨道及其稳定流形Fig.3 Stable manifolds associated with the Earth-Moon L2 point

1.3 地–月转移与稳定流形入轨

根据Oberth效应，同等速度增量条件下，近月点制动高度与轨道能量的改变量成反比，因此本文的地–月转移轨道的近月点高度设计为100 km，通过近月点制动，探测器进入近月点高度100 km的Halo轨道稳定流形。对Az=8 000 km北族Halo轨道及其稳定流形计算，并对100 km近月点高度对应的稳定流形进行搜索，得到稳定流形的近月点时刻tp与状态Xp。本文采取对稳定流形近月点状态Xp施加脉冲机动ΔV1并逆向递推至近地点的方式，将近地点高度修正到200 km。对于该Halo轨道，近月点脉冲约为250 m/s，地月转移时间约120 h，稳定流形转移约11 d进入目标Halo轨道。地月转移与稳定流形入轨轨迹如图4所示。

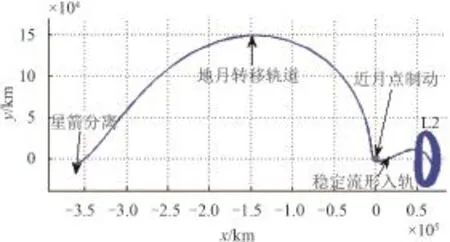
图4 从地球发射至地–月L2点Halo轨道入轨的轨迹Fig.4 Flight trajectory from the Earth to Earth-Moon L2 Halo orbit

1.4 Halo轨道保持控制

地–月L2点附近的运动不稳定性以及Halo轨道设计初值的偏差会导致探测器轨迹发散而偏离标称轨道，因此，本文设计每1/2轨道周期执行一次轨道保持控制。采用轨迹延续控制方法[7]，考虑定轨位置误差1 km，速度误差0.01 m/s，控制误差5%，控制间隔7.35 d，采用Monte-Carlo仿真50次轨控过程，轨控后的轨迹如图5所示，年平均控制量约为18 m/s。

图5 地–月L2点Halo轨道保持控制Fig.5 Statekeeping control of Earth-Moon L2 orbit

除了近月点制动、Halo轨道保持控制之外，探测器的燃料预算还应考虑地月转移段针对火箭入轨偏差的轨道修正，本文对该修正量设计272 m/s的速度增量，则寿命3年的中继星任务总的速度增量为576 m/s。若卫星干重300 kg，采用单组元轨控推进器系统，发动机推力300 N，比冲200 s，若燃料携带200 kg，卫星总重500 kg，则燃料消耗约127 kg。

2 地–月三体系统轨道自主导航

研究表明，地–月/日–地三体系统引力场的不对称性可以用来实现卫星的星–星测距自主定轨[15-18]，而三体系统平动点附近的轨道远离主天体，且受两大主天体引力共同作用，可以实现自主定轨算法的快速收敛。该自主定轨的核心思想是基于sat1-sat2测距值与两颗卫星的距离估计值偏差来估计两星的状态偏差，从而对两星的状态量进行修正。本节对卫星自主定轨的运动方程与观测方程进行设计，并开展自主定轨的仿真计算。

2.1 运动方程与观测方程

中继通信卫星的状态——位置矢量与速度矢量记为

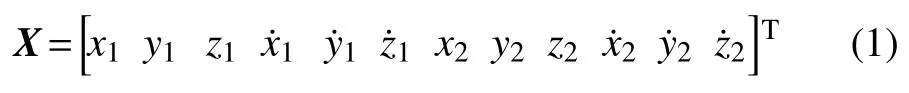
其中：下标1、2分别表示sat1和sat2。卫星的运动方程为

该方程的动力学模型考虑日、地、月质点引力场。卫星状态偏差∆X和观测值∆Y的残差为

其中：X*（t）是卫星状态的估计值；Y*（t）是采用状态估计值X*（t）计算的观测量估计值。观测量与状态量之间用函数关联

其中：G是通过卫星状态计算观测量的函数

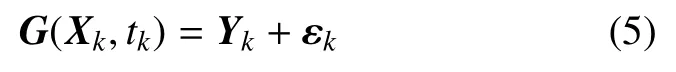
其中：εi是观测误差；Xk、Yk分别为滤波第k步时的状态与观测量。如果测量值是星–星距离ρ及相对速度，则观测量Yk与状态量Xk之间关联函数为

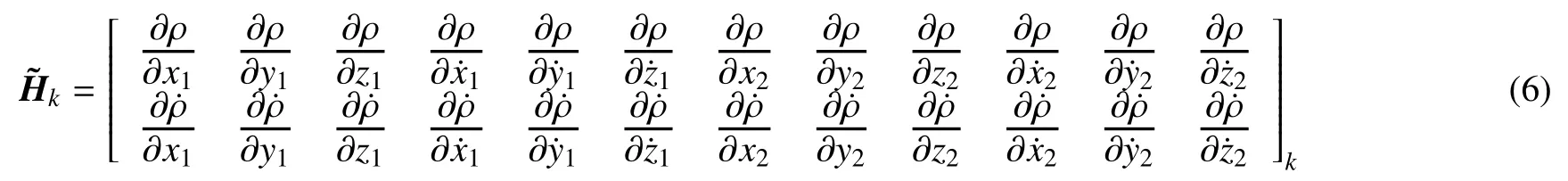
tk-1时刻的状态偏差可以由状态转移矩阵映射到tk时刻

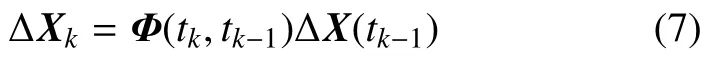
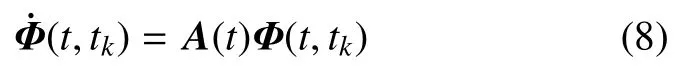
2.2 自主导航的数值仿真

Halo轨道位于地–月L2点，z轴幅值Az=8 000 km，月球极轨是高度为1 000 km的圆轨道，两颗卫星的初始历元时刻均为2019年1月1日。滤波开始时刻t0的轨道估计值与真实状态的偏差分别为位置3 km，速度0.3 m/s （1σ），星–星测距误差1 m （1σ）。本文的标称轨道采用日–地–引力模型递推获得，星–星测距的观测值来源于标称轨道。采用扩展卡尔曼滤波，对半个Halo轨道周期约7.5 d的数据开展自主定轨数值仿真，星–星测距采样时间间隔为100 s，同时获得两颗探测器的轨道数据，月球极轨卫星与Halo轨道的滤波过程分别如图6和图7所示。

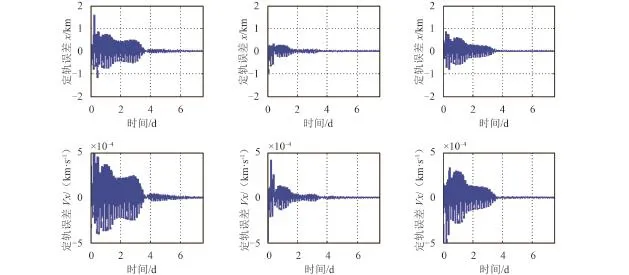
图6 环月轨道自主定轨收敛曲线Fig.6 Filtering curves of lunar orbit from auto-navigation algorithm

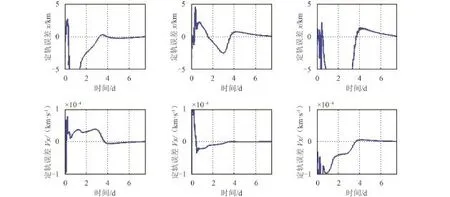
图7 Halo轨道自主定轨收敛曲线Fig.7 Filtering curves of Halo orbit from auto-navigation algorithm

图6所示的环月极轨收敛曲线的振荡频率较高，对应为环月探测器的轨道周期，约为3.5 h。在星–星相对测距定轨滤波的第4 d，位置误差均收敛到20 m以内，速度误差小于1 cm/s。如图7所示，对于L2点Halo轨道的定轨滤波，收敛时间较环月轨道稍长，在第6 d左右，可以将轨道维持误差降低到250 m，轨道速度误差收敛到2 cm/s以内。从仿真结果来看，环月轨道的定轨精度优于地–月L2点Halo轨道。为提高星–星测距定轨在地–月系统中继通信卫星自主导航中的实用价值，还需考虑状态方程与真实动力学环境的模型误差，作者将对这一问题继续开展深入研究。

3 结 论

本文以月球背面中继通信卫星轨道自主导航为背景，重点针对月球极轨卫星与地–月L2点Halo轨道组成的中继通信网络的轨道设计与自主定轨问题开展研究，结论如下。

1）采用近月点制动、Halo轨道稳定流形入轨方式进入地–月L2点Halo轨道，并考虑轨道中途修正及Halo轨道状态保持，总的速度增量约为576 m/s，若卫星干重为300 kg，则可以将卫星发射重量降低到500 kg以内。

2）在考虑星–星测距误差1 m，轨道初始偏差3 km和0.3 m/s条件下，仅采用星–星测距作为观测量可以实现地–月L2点Halo轨道和环月轨道自主定轨滤波过程的收敛，6 d数据采集可以实现Halo轨道定轨位置误差和速度误差分别小于250 m和2 cm/s。

[1]Farquhar R W.Lunar communications with libration-point satellites [J].Journal of Spacecraft and Rockets，1967，4（10）：1383-1384.

[2]Gordon D P.Transfers to Earth-Moon L2 Halo orbits using lunar proximity and invariant manifolds [D].Indiana：Purdue University，2008.

[3]Li M T，Zheng J H.Impulsive lunar Halo transfers using the stable manifolds and lunar flybys [J].Acta Astronautica，2010，66：1481-1492.

[4]Crawford I A，Anand M，Cockell C S，et al.Back to the Moon：the scientific rationale for resuming lunar surface exploration [J].Planetary and Space Science，2012，74：3-14.

[5]刘磊，胡松杰，唐歌实，等.月球中继通信与导航的研究进展与建议[C]// 中国宇航学会深空探测技术专业委员会第十届学术年会.太原：中国宇航学会深空探测技术专业委员会，2013.Liu L，Hu S J，Tang G S，et al.Research progress and suggestions on the communication and navigation of lunar relay[C]// The 10th Conference of Committee of Deep Space Exploration Technology，Chinese Society of Astronautics.Taiyuan：Committee of Deep Space Exploration Technology，Chinese Society of Astronautics，2013.

[6]Lian Y J，Gomez G，Masdemont J J，et al.Station-keeping of real Earth-Moon libration point orbits using discrete-time sliding mode control [J].Communications in Nonlinear Science and Numerical Simulation，2014，19（10）：3792-3807.

[7]Folta D C，Pavlak T A，Haapala A F，et al.Earth-Moon libration point orbit station keeping：theroy，modeling，and operations [J].Acta Astronautic，2014，94（1）：421-433.

[8]黄翔宇，黄江川，李骥，等.基于图像测量数据的目标接近段自主导航方法研究与试验[J].中国科学：技术科学，2013，43（7）：748-754.Huang X Y，Huang J C，L J，et al.Research and experiment on the target approach segment autonomous navigation method based on image measurement data[J].Scientia Sinica Technologica，2013，43（7）：748-754.

[9]崔平远，高艾，于正湜.火星着陆自主导航方案研究进展[J].深空探测学报，2014，1（1）：18-27.Cui P Y，Gao A，Yu Z S.Reserch progress of autonomous navigation scheme for Mars landing[J].Journal of Deep Space Exploration，2014，1（1）：18-27.

[10]Qian Y J，Li C Y，Jing W X，et al.Sun-Earth-Moon autonomous orbit determination for quasi-periodic orbit about the translunar libration point and its observability analysis [J].Aerospace Science and Technology，2013，28：289-296.

[11]黄翔宇，崔平远，崔祜涛.深空自主导航系统的可观性分析 [J].宇航学报，2006，27（3）：332-337.Huang X Y，Cui P Y，Cui H T.Observability analysis of deep space autonomous navigation system[J].Journal of Astronautics，2006，27（3）：332-337.

[12]Sheikh S I，Pines D J，Ray P S，et al.Spacecraft navigation using X-ray pulsars [J].Journal of Guidance，Control，and Dynamics，2006，29（1）：49-63.

[13]帅平，陈绍龙，吴一帆，等.X射线脉冲星导航原理 [J].宇航学报，2007，28（6）：1538-1543.Shuai P，Chen S L，Wu Y F，et al.Navigation principles using X-ray pulsars[J].Journal of Astronautics，2007，28（6）：1538-1543.

[14]Psiaki M L.Autonomous orbit determination for two spacecraft from relative position measurements [J].Journal of Guidance，Control，and Dynamics，1999，22（2）：305-312.

[15]Hill K，Parker J，Born G H，et al.A Lunar L2 navigation，communication，and gravity mission [C]// AIAA/AAS Astrodynamics Specialist Conference.Keystone，CO：AIAA，2006.

[16]Hill K，Born G H.Autonomous interplanetary orbit determination using satellite-to-satellite tracking [J].Journal of Guidance，Control，and Dynamics，2007，30（3）：679-686.

[17]Hill K，Born G H.Autonomous orbit determination from lunar Halo orbits using crosslink range [J].Journal of Spacecraft and Rockets，2008，45（3）：548-553.

[18]Leonard J M，Jones B A，Villalba E J，et al.Absolute orbit determination and gravity field recovery for 433 Eros using satellite-tosatellite tracking [C]// AIAA/AAS Astrodynamics Specialist Conference.Minneapolis，Minnesota：AIAA，2012.

[19]高有涛，徐波，熊欢欢.一种提高导航卫星星座自主定轨精度的方法研究 [J].宇航学报，2014，35（10）：1165-1175.Gao Y T，Xu B，Xiong H H.A method for improving accuracy of autonomous orbit determination for navigation constellation[J].Journal of Astronautics，2014，35（10）：1165-1175.

[20]Richardson D L.Analytic construction of periodic orbits about the collinear points [J].Celestial Mechanics and Dynamical Astronomy，1980，22：241-253.

[21]Howell KC，Pernicka H J.Numerical determination of Lissajous trajectories in the restricted three-body problem [J].Celestial Mechanics and Dynamical Astronomy，1998，41（1），107-124.

[22]Jorba Á.Numerical computation of the normal behaviour of invariant curves of n-dimensional maps [J].Nonlinearity，2001，14（5）：943-976.

王亚敏（1987– ），男，博士，助理研究员。主要研究方向：深空轨道设计与优化。

通信地址：上海市浦东新区海科路99号4号楼（201210）

电话：15026989781

E-mail：wangyam09@163.com

张永合（1977– ），男，博士，副研究员。本文通讯作者。主要研究方向：卫星总体设计，星–星跟踪重力场测量卫星的无拖曳控制。

通信地址：上海市浦东新区海科路99号4号楼（201210）

电话：13585840296

E-mail：yonghe.zhang@mail.sim.ac.cn

Autonomous Navigation of Three-Body Trajectory Based on Asymmetric Gravity Field

WANG Yamin1,2，LIU Yinxue3，JIANG Jun1,2，SUN Yukun1,2，ZHANG Yonghe1,2
（1.Shanghai Engineering Center for Microsatellites，Shanghai 201210，China；2.Key Laboratory of Microsatellite，Chinese Academy of Sciences，Shanghai 201210，China；3.School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China）

In this paper，the autonomous orbital determination method with the background of communication relay net for the Moon is investigated.Two satellites，distributing on a lunar polar orbit and an Earth-Moon L2 Halo orbit，are proposed to cover the far side of the Moon and the lunar polar area.Based on the asymmetric three-body gravity field，the absolute orbital determination can be done by the sole satellite-satellite ranging.The autonomous orbital determination will contribute significantly to the autonomous management of deep space spacecraft.Numerical simulation indicates that the position error and velocity error can be reduced to the order of 100 m and 1cm/s respectively.This orbital determination method can be expanded to the autonomous navigation of multiple satellites movements around an irregular asteroid.

satellite-to-satellite tracking；autonomous navigation；Earth-Moon system；communication relay；deep space exploration

V41

：A

：2095-7777（2017）01-0026-05

10.15982/j.issn.2095-7777.2017.01.004

王亚敏，刘银雪，蒋峻，等.基于引力场不对称性的三体系统轨道自主导航[J].深空探测学报，2017，4（1）：26-30，37.

Reference format：Wang Y M，Liu Y X，Jiang J，et al.Autonomous navigation of three-body trajectory based on asymmetric gravity field [J].Journal of Deep Space Exploration，2017，4（1）：26-30，37.

[责任编辑：宋宏，英文审校：任树芳]

2016-11-01

2016-12-06

国家重点研发计划（2016YFB0501103）