图木舒克市南北湖大桥工程连拱内力分析

孙茂辉 牛 浩

(中交第四公路工程局有限公司，北京 100022)



图木舒克市南北湖大桥工程连拱内力分析

孙茂辉 牛 浩

(中交第四公路工程局有限公司，北京 100022)

采用换算刚度法，对一座9跨不等刚度墩半圆弧无铰拱内力进行计算分析，并基于结构等效换算刚度与内力影响线，得出不等跨连拱内力特点，以期为类似结构分析提供参考。

连拱内力，换算刚度法，无铰拱，内力影响线

0 引言

拱桥作为受力结构良好、应用基础广泛的桥型结构，在我国桥梁建设中有着重要的地位，特别是在山区桥梁和市政桥梁中，拱桥以其轴向受力弯矩小、桥型结构形式美观的优势，广泛受到设计者偏爱。

连拱与单拱在受力上不同，由于单拱只需要考虑单跨结构内力影响，故其内力分析相对简单；而连拱由于跨与跨之间存在着内力的相互作用，其受力特点相对复杂，结构内力分析具有一定的难点，且不等跨连拱由于各拱之间刚度不同，其内力也有相应的区别。

众多学者[1-5]对连拱的内力分析进行了探讨，本文以图木舒克市南北湖大桥工程为工程背景，以换算刚度法为研究方法，从理论角度，对该9跨不等刚度墩半圆弧无铰拱内力计算进行分析，基于结构等效换算刚度与内力影响线，得出不等跨连拱内力，以期为类似结构提供参考。

1 工程背景

图木舒克市南北湖大桥工程是该市的引水入市拱桥工程之一，全桥长98 m，为9孔不等跨等刚度墩半圆弧无铰拱，下部结构采用扩大基础，为典型的连拱。设计荷载等级为公路Ⅰ级，净跨径l0为6.4 m～8.0 m不等，净矢跨比f0/l0为1/2，拱顶填料平均厚度为0.3 m。

拱圈为C40现浇钢筋混凝土，容重γ1=25 kN/m3，弹性模量E1=3.25×104MPa；侧墙、护拱为7.5号砂浆砌块、片石，拱腹填料及侧墙平均容重γ2=20 kN/m3；下部结构采用C25混凝土，容重γ1=25 kN/m3，弹性模量E2=2.8×104MPa。

拱桥桥型布置图如图1所示。

2 换算刚度

2.1 拱圈弹性常数计算

因为该拱桥为不等跨等刚度9孔连拱桥，各孔跨度不尽相同，故应考虑恒载、温度，以及活载作用下的连拱效应，考虑到各孔主拱圈配筋相同，且第5孔跨度最大，故第5孔受力最为不利。首先计算拱圈弹性常数。

拱圈为等截面圆弧线拱，半圆心角为90°。拱脚处与墩身固结，所以按照无铰拱计算。拱桥的弹性常数有抗推刚度K和其相干系数T，抗弯刚度S和传递抗弯刚度CS，计算如下式：

2.2 桥墩弹性常数计算

桥墩采用的是重力式矩形桥墩，下部结构采用扩大基础。桥墩为等截面重力式墩。桥墩的弹性常数的计算如下所示：

2.3 换算刚度计算

求出拱、墩的弹性常数后，荷载作用下的连拱计算可以采用不同的简化方法。考虑“换算刚度法”计算精度较高，使用也比较方便，为保证拱、墩内力的计算精度，采用换算刚度法进行计算。

本桥为不等跨，计算拱中最大活载内力时，以荷载作用在跨度最大的中孔(第5孔)时，该孔受力最为不利。

换算刚度的计算如下所示：

∑KA=∑KB=KA,1+K5=6.70×106kN/m。

∑TA=∑TB=K5-TA,1=-1.54×107kN。

∑SA=∑SB=SA,1+S5=6.31×107kN·m。

3 固定拱内力计算

3.1 活载内力影响线计算

由于按连拱计算结构内力是等于按固定拱计算的内力与连拱作用引起的内力之和，故在计算连拱作用之前，先要确定按固定拱计算时拱圈的内力。

拱结构是超静定结构，其内力是荷载内力与多余未知力的函数，在确定拱的内力影响线时，先计算三次超静定结构的多余未知力Z，H，V的影响线，再将多余未知力与荷载内力叠加，即得圆弧拱的内力影响线。取图2作为基本结构，由于结构对称，只需计算左拱内力影响线即可。

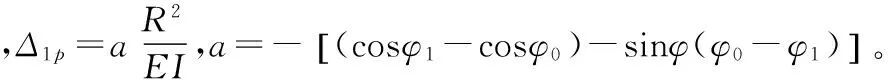
由此可计算拱任意截面c的内力如下：

弯矩：Mx=Z-Hy±VRsinφ+Mp。

轴力：Nx=Hcosφ+(P∓V)sinφ。

剪力：Qx=±Hsinφ∓(P∓V)cosφ。

3.2 恒载内力计算

由于恒载作用的对称性，在拱圈弹性中心仅有弯矩和水平力两个多余未知力。本桥为实腹式圆弧拱，可将上部恒载分为三个部分：桥面铺装、拱腹填料和拱圈，计算时采用弹性重心法先对每一部分分别计算内力，然后叠加。计算如下：

弯矩：Z=(B1g1+B2g2+B3g3)R2。

水平力：H=(c1g1+c2g2+c3g3)R。

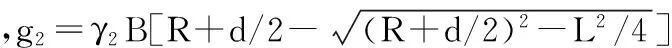
则主拱圈任意截面内力可根据静力平衡条件求得。

拱顶截面：M=Z-Hys=224 kN·m。

N=H=1 270 kN。

其他截面：M=Z-Hy+Mp，N=Hcosφ+Ppsinφ。

其中，Pp=(a1g1+a2g2+a3g3)R。

Mp=-(b1g1+b2g2+b3g3)R2。

3.3 温度内力计算

由于温度作用在弹性中心处产生的水平力：

其中，β为系数，取26.724；α为材料线膨胀系数，对混凝土取1.0×10-5；Δt为温度变化值，上升为正，下降为负。

4 连拱影响线计算

在无铰连拱中，一般竖向位移的影响可以忽略不计，只考虑水平位移和转角的影响。连拱内力则可以计为固定拱内力和水平位移引起内力以及转角引起内力之和。

参数计算如下所示：

A1=∑KA∑SA-(∑TA)2=3.44×1015。

A2=K2∑SA-T2∑TA=8.27×1013。

B1=A2。

B2=A1。

R2=A1B2-A2B1=1.18×1031。

变位参数为：

。

连拱内力影响线的计算:

连拱作用下主拱圈内力影响线见图3。

5 主拱圈内力计算

对比按固定拱计算拱圈内力和连拱效应计算拱圈内力的影响线可知，连拱作用下的拱圈截面的弯矩数值有所提高，而拱脚推力则有所减小。在布载时，可按截面弯矩最大布载。内力计算的主要内容包括：恒载计算、汽车及人群荷载计算、温度荷载。

活载内力计算包括汽车荷载。本桥整体结构计算采用汽车荷载，荷载等级为公路Ⅰ级，由均布荷载和集中荷载组成，均布荷载qk=10.5kN/m，集中荷载本桥取Pk=194kN(计算跨径L=8.4m)，剪力计算时取1.2Pk。均布荷载qk作用于结构产生最不利影响的同号影响线上，集中荷载Pk作用于影响线的最大值处。

拱顶弯矩影响线及其布载方式如图4所示。

均布荷载在正弯矩处布载，集中荷载作用在跨中。则拱顶最大弯矩Mmax=ξ(qkωm+Pkηmax)=361kN·m。

3/8L弯矩影响线及其布载方式如图5所示。

计算最大正弯矩时，均布荷载布置在影响线正区域，集中荷载作用在L/4跨。则3/8L最大弯矩Mmax=ξ(qkωmB+Pkηmax)=354kN·m。

由以上分析，得出连拱作用下荷载组合内力值，相应荷载内力如表1所示。

表1 荷载组合内力值

荷载组合拱顶L/4截面拱脚MmaxNmaxMmaxMminNmaxMminHmaxVmax基本组合Sud1189.22249.221702492.8-1013.64929.21189.22249.2短期组合Ssd773.11690.215981880.3-602.53807.6773.11690.2长期组合Sld664.81592.41491.81773.6-502.43614.8664.81592.4注:M为弯矩,kN·m;N为轴力,kN;H为水平推力,kN

6 结语

本文以图木舒克市南北湖大桥工程为工程背景，建立圆弧拱基本结构受力方程，通过换算刚度法将拱圈刚度与桥墩刚度进行换算，并分析结构内力影响线，通过理论推导，得出连拱各个不同截面位置的影响线分布图，并以此分析连拱在恒载、活载及温度荷载作用下结构的内力情况。根据规范荷载组合要求，对连拱结构进行短期状态和长期状态荷载组合。通过分析表明，换算刚度法计算精度高、计算简便，能够满足设计内力计算需求。同时，由分析结果可知，连拱内力沿拱轴线分布趋势符合一般拱桥状态，需要重点考虑拱脚位置弯矩与水平推力的影响。

[1] 李金国,曹 茜.三跨等截面圆弧拱连拱计算[J].公路工程,2011,36(3):102-104.

[2] 何延松.无铰连拱计算[J].北方交通,2011(3):47-50.

[3] 杨爱武.连拱拱桥结构设计分析[J].安徽建筑大学学报,2008,16(1):69-72.

[4] 许生超.用直接刚度法计算连拱影响线[J].重庆交通大学学报(自然科学版),1984,3(4):92-99.

[5] 王国鼎.不等跨无铰连拱换算刚度的计算[J].公路工程,1984(3):67-76.

Internalforceanalysisofcontinuousarchbridgeforsouth-northlakebridgeinTumushukecity

SunMaohuiNiuHao

(CCCCFourthHighwayEngineeringCo.,Ltd,Beijing100022,China)

In order to analyze the internal force characteristics of continuous arch bridge, a 9 spans semicircle non hinged arch bridge with unequal stiffness piers was analyzed by equivalent stiffness method combined with the engineering practice. Based on the equivalent stiffness and internal force influence line of the structure, the internal force of unequal span arch is obtained, which is provided reference for similar structure.

internal force of continuous arch, equivalent stiffness method, non hinged arch bridge, internal force influence line

1009-6825(2017)08-0165-03

2017-01-05

孙茂辉(1978- )，男，工程师； 牛 浩(1987- )，男，工程师

U441

A