熔喷过程中纤维直径再次变大的模拟与验证
谢 胜, 韩万里
(嘉兴学院 材料与纺织工程学院, 浙江 嘉兴 314000)
熔喷过程中纤维直径再次变大的模拟与验证
谢 胜, 韩万里
(嘉兴学院 材料与纺织工程学院, 浙江 嘉兴 314000)
为直观表达熔喷过程中气流对纤维的拉伸作用,对熔喷过程中的纤维运动进行了数值模拟。首先将熔喷过程中的纤维看作是由麦克斯韦(Maxwell)元件连接的珠子;之后将已知的纤维速度、纤维温度数据加载到纤维模型上,通过拉格朗日法数值模拟预测纤维在熔喷过程中的运动速度、纤维直径等信息。模拟结果表明,纤维在远离喷丝孔的过程中,由于气流速度、气流温度逐渐衰减,致使纤维受到气流力的作用逐渐减弱,若气流力小于纤维自身的黏弹力,纤维会在黏弹力的作用下回缩,在宏观上表现为纤维直径的再次增大。最后在一定实验条件下,利用线下方法测量了熔喷纤维的直径,实验结果也验证了熔喷过程中纤维直径会有再次变大的现象。
熔喷; 纤维轨迹; 运动模拟; 纤维直径
熔喷是一步法生产微米级纤维的非织造技术,由于微米级纤维具有孔隙度高和比表面积大等特点,使得熔喷非织造布在过滤防护、医疗卫生及保暖材料等领域有着重要的应用[1]。
熔喷纤维是聚合物经气流牵伸而成的纤维,熔喷非织造布中纤维平均直径在1~10 μm范围内。由于熔喷过程中气流速度很高,纤维的运动也相应很复杂,且纤维直径较细,所以用实验方法在线测量纤维直径显得尤为困难,并且实验测量无法得到纤维在拉伸过程中的速度和受力等信息,无法表达气流对纤维的拉伸机制。鉴于实验测量的局限性,本文采用数值模拟方法来研究纤维直径。
首先对熔体纤维进行分析,建立符合纤维特性的理论模型,然后通过拉格朗日法模拟了纤维从喷丝孔运动到接收帘子这一过程,并研究了纤维在这一过程中速度、直径等数值的变化。通过本文的模拟发现了熔喷过程中纤维直径再次增大的现象,即纤维在喷丝孔处的直径最大(不考虑挤出膨大效应),受高速气流的吹喷作用纤维直径迅速减小,之后纤维直径会有一个重新增大的过程。最后用线下测量的实验方法证实了在一定实验条件下熔喷过程中纤维直径会有再次增大这一现象。
1 模 拟
1.1 纤维模型
图1示出熔喷过程中气流对纤维的作用示意图。聚合物熔体受到喷丝孔附近高温、高速气流的吹喷作用而迅速拉伸,随纤维远离喷丝孔,纤维的温度逐渐下降,最终纤维固化并落到接收帘子上形成非织造产品。本文中的纤维指的是聚合物熔体。

图1 熔喷过程中气流对纤维的作用示意图Fig.1 Schematic of fiber-attenuating by air in melt blowing process
熔喷过程中,熔融态纤维具有典型的黏弹特征。本文具有黏弹特性的纤维采用的是将弹簧与黏壶串联连接的珠子表示,即Maxwell模型,在此模型中纤维质量集中在珠子上。图2示出聚合物纤维的Maxwell模型示意图。
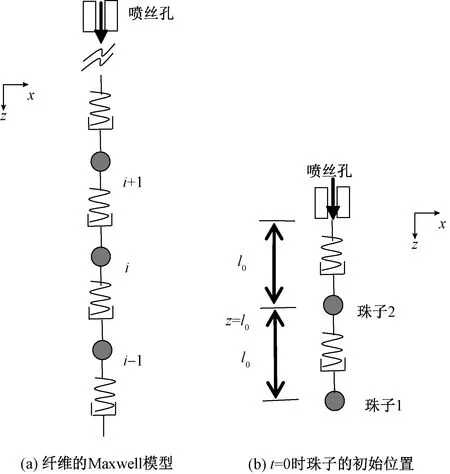
注:i—第i个珠子; l0—初始时刻相邻两个珠子之间的距离。图2 熔喷纤维模型Fig.2 Model of melt-blowing fiber.(a) Maxwell model of fiber; (b) Initial location of beads at t=0
1.2 纤维在气流场中的受力
1.2.1 气流力
气流对纤维的作用力与纤维的表面积有关,其表达式[2-3]为
(1)
式中:Fp为纤维受到的气流力;Cp为系数;ρa为空气密度;vrel为气流与纤维的相对速度;df为纤维直径;lf为纤维片段的长度。
Cp=0.78(ReD)-0.61
(2)
(3)
式中:ReD为雷诺数;μa为空气的黏度。
1.2.2 黏弹力
纤维的内应力可用下式[4]来表示:
(4)
式中:E为弹性模量;σi-1,i为纤维微元(i-1,i)内应力;li-1, i为纤维微元(i-1,i)的长度;ν为应力松弛时间,并有:
(5)
式中μf为聚合物纤维的黏度。
将式(4)和(5)进行整理,得
(6)
则黏弹力Fvis可表示为
Fvis=0.25πdi-1,i2σi-1,i
(7)
式中:di-1, i为纤维元(i-1,i)的直径;σi-1,i为纤维(i-1,i)的内应力。
1.2.3 纤维与气流的热量交互
由式(6)可知,纤维的黏度μf是求解内应力的关键,依赖于纤维的温度T。气流温度与纤维温度之间的传递关系[5]为
(8)
式中:Ci为纤维的比热容;h为传热系数;Ti为珠子i的温度;Tai为珠子i处气流温度。
而传热系数h与努塞尔数Nu的关系为
(9)
式中ka为空气的热导率。
根据Andrews[6]、Kase[7]、Mueller[8]以及Champangne[9]等的研究,努塞尔数Nu为
(10)
式中:ψ为相对速度在纤维轴线上的分量;Nu90为纤
维轴线与气流方向垂直时的Nu。
Nu90=0.764Rei0.38
(11)
(12)
式中:Rei为珠子i处的雷诺数;vrel,i为在珠子i处气体与纤维的相对速度;df,i为珠子i处的纤维直径。
根据式(9)~(12)就可推导出纤维温度T,另外,纤维密度ρf、纤维比热容Ci及纤维的黏度μf都与纤维温度有关[3,10]:
(13)
Ci=0.366 9+2.42×103Tfi
(14)
(15)
式中:ρfi指珠子i处的纤维密度;Tfi为珠子i处的纤维温度;μfi为珠子i处黏度。
1.2.4 模拟步骤
模拟中用到的工艺参数[5,11]如表1所示。

表1 丙纶材料属性及设置的工艺参数Tab.1 Material properties and technological parameters used in simulation
气流速度vaz和气流温度Taz数据[11]分别为
(16)
(17)
2)t=0时刻,在喷丝孔下方设置有2个珠子,如图2(b)所示。初始直径设为5×10-4m;珠子1与珠子2之间的距离为l0=1×10-3m,初速度为0.1 m/s;2个珠子都位于z轴上。根据式(16)和(17),将珠子的属性计算好,并计算初始时刻受到的气流力。
计算循环时间步长设为1×10-5s,计算珠子在1×10-5s时刻珠子新的位置。计算第1次由于珠子位置变化导致的内应力。并更新纤维属性与受力。
3)按照质量守恒原理,更新珠子直径。
4)重复步骤3)和4),设置喷丝孔每隔0.01 s吐出1个珠子。
5)因为珠子1始终不会受到下方珠子的作用力,因此取珠子2到达接收帘子时停止。
2 模拟结果与实验验证
2.1 模拟结果
图3示出了模拟过程中不同时刻纤维(珠子)的运动轨迹,从左至右依次表示了在t=0.075 0 s、t=0.108 9 s和t=0.157 5 s时纤维的轨迹。在t=0.075 0 s时,珠2在喷丝孔下方0.1 m处,纤维轨迹由8个珠子组成;在t=0.108 9 s时,珠2在喷丝孔下方0.2 m处,纤维轨迹由11个珠子组成;在t=0.157 5 s时,纤维轨迹由17个珠子组成,珠2在喷丝孔下方0.35 m处,即到达设定的接收帘子上。
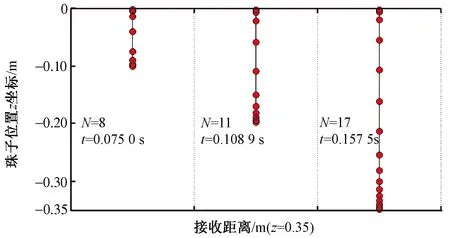
图3 模拟过程中纤维在不同时刻的运动轨迹Fig.3 Fiber path at different time during simulation
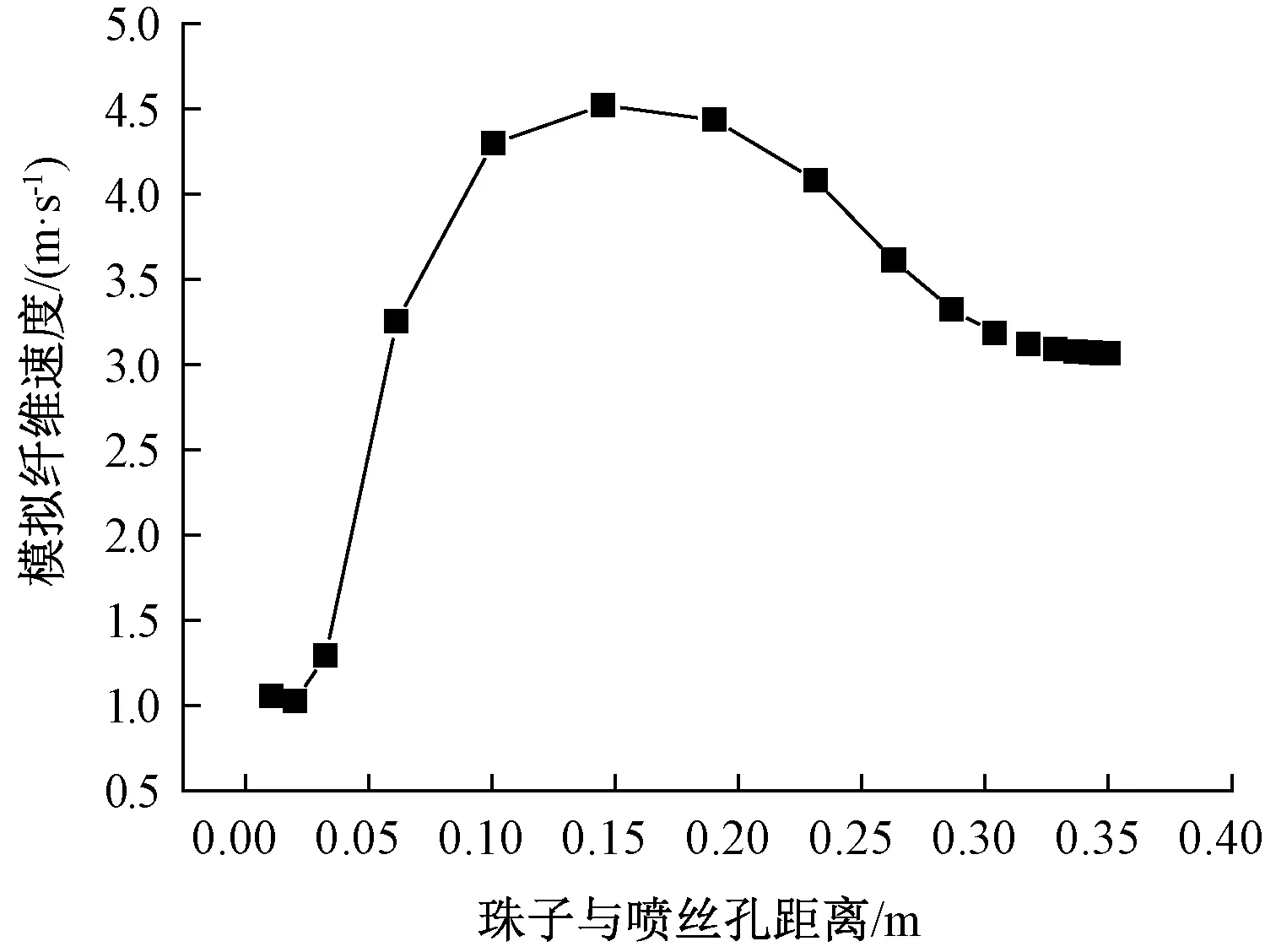
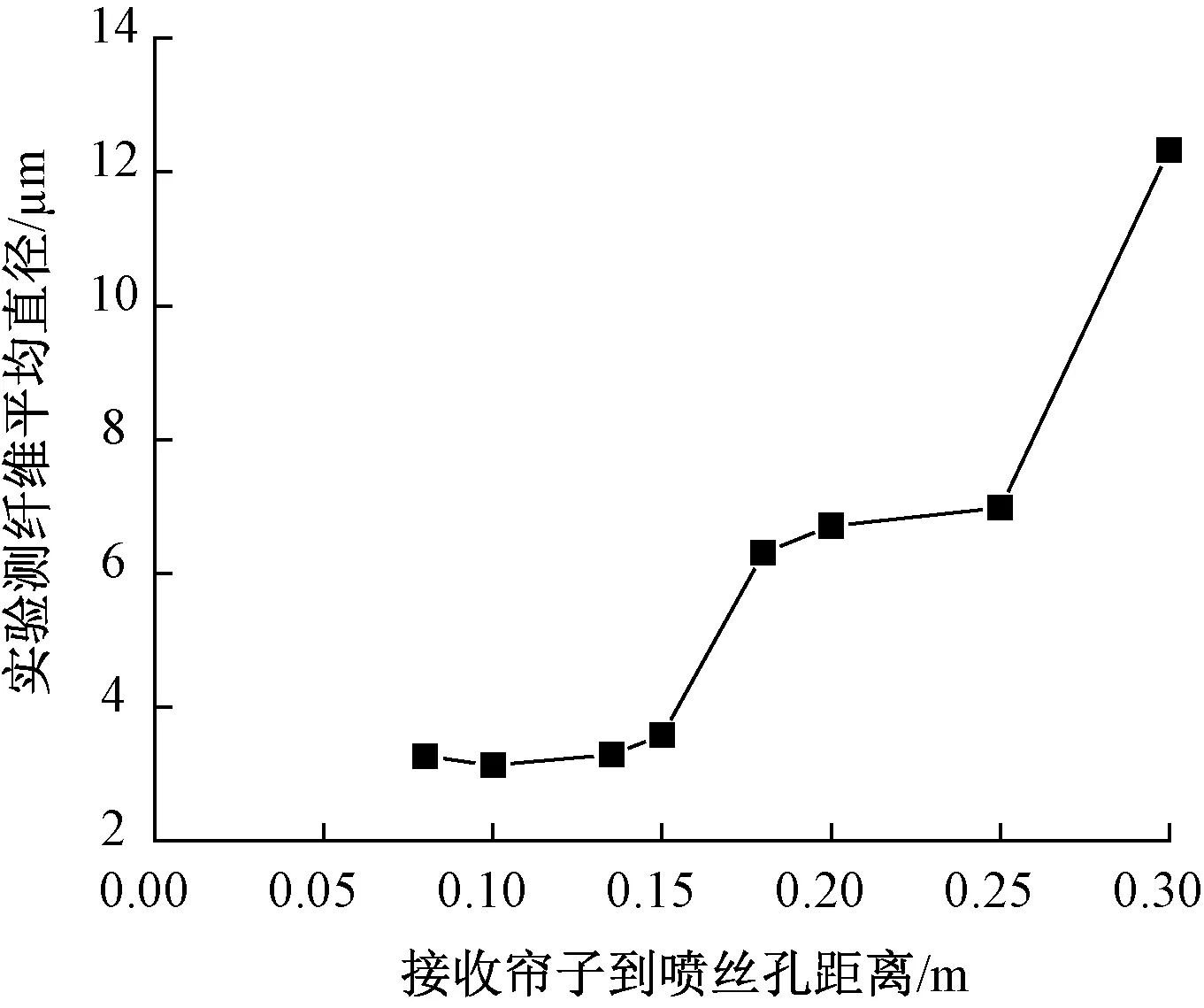
图4示出模拟纤维下落过程中其直径的变化。可看出,纤维在离开喷丝孔很短的距离(0≤z≤0.05 m)内纤维直径迅速减小,之后纤维直径的减小并不明显(0.05 m 图4 模拟纤维下落过程中其直径的变化Fig.4 Variation of fiber diameter during process of simulation 这种纤维直径的再次变大现象也可由模拟得到的纤维速度侧面反映出来,图5示出模拟过程中纤维速度的变化规律。可看出,在离开喷丝孔后纤维先做较快升速运动,并在z=0.15 m处纤维速度达到最大值,约为4.5 m/s,而后纤维的速度逐渐下降,这就导致后面纤维有追上前面纤维的趋势,进而表现出纤维直径的再次变大。 图5 模拟纤维下落过程中其速度的变化Fig.5 Variation of fiber velocity during process of simulation 2.2 实验验证 图6示出在一定的实验条件下,线下测量得到的纤维直径。线下测量是指先在接收帘子上得到纤维,再测量纤维直径。可看出,当纺丝距离从0.1 m增大到0.3 m的过程中,纤维直径逐渐增大。这一实验数据的获得验证了以上理论模拟的正确性。 图6 熔喷纤维直径随接收距离的变化规律Fig.6 Variation of fiber diameter with distance of collecting in melt-blowing process 关于本文中纤维直径的再次变大现象,需要说明几点:1)不一定所有的熔喷过程中都会有纤维直径的再次增大现象,因为纤维直径的再次变大现象是建立在纤维未固化的基础上。若纤维固化之前,纤维黏弹力大于受到的气流力,那么纤维直径会出现再次变大的现象;若纤维已经固化,之后无论黏弹力是否大于受到的气流力,纤维的伸长都不会发生变化,即直径也不会再次变大;2)在熔喷过程中可能会发生纤维直径的再次增大现象,这种现象是否出现体现在熔喷气流场的设计是否合理,良好的气流场分布需具备在纤维固化之前气流速度还大于纤维速度,使得纤维继续保持被牵伸的趋势。纤维直径的再次变大现象对熔喷最终产品是不利的,消除纤维直径的再次变大是熔喷工艺控制需要注意和克服的。 1)对熔喷过程中熔体纤维建立Maxwell模型,并模拟了纤维的运动,通过模拟预测到纤维直径在被气流牵伸变细后可能会出现直径的再次变大现象。 2)通过一定条件下的熔喷实验,验证了熔喷过程中纤维直径再次变大的模拟结论。 3)模拟得到的纤维直径再次变大现象对熔喷产品来讲是不利的,因此,对流场进行优化设计,消除或抑制纤维直径再次变大现象是值得探讨的。 FZXB [1] 柯勤飞, 靳向煜. 非织造学[M]. 上海:东华大学出版社, 2010:303. KE Qinfei, JIN Xiangyu. Nonwovens[M]. Shanghai: Donghua University Press, 2010:303. [2] RAO R S, SHAMBAUGH R L. Vibration and stability in the melt blowing process[J]. Industrial Engineering Chemistry Research, 1993, 32: 3100-3111. [3] MARLA V T, SHAMBAUGH R L. Three-dimensional model of the melt-blowing process[J]. Industrial Engineering Chemistry Research, 2003, 42: 6993-7005. [4] RENEKER D H, YARIN A L, FONG H, KOOMBHONGSE S. Bending instability of electrically charged liquid jets of polymer solutions in electrospinning[J]. Joural of Applied Physics, 2000, 87: 4531-4547. [5] 孙亚峰, 微纳米纤维纺丝拉伸机理的研究[D]. 上海:东华大学, 2011: 108. SUN Yafeng. Investigation of micro-nano fiber forma-tion[D]. Shanghai: Donghua University, 2011:108. [6] ANDREWS E H. Cooling of a spinning threadline[J]. British Journal of Applied physics, 1959, 10(1): 39. [7] KASE S, MATSUO T. Studies on melt spinning. I. fundamental equations on the dynamics of melt spin-ning[J]. Journal of Polymer Science Part A, 1965, 3: 2541. [8] MUELLER A C. Heat transfer from wires to air in parallel flow[J]. Transactions of the Institution of Chemical Engineers, 1942, 38: 613. [9] CHAMPAGNE F H, SlEICHER C A, WEHRMANN O H. Turbulence measurements with inclined hot-wires. part I. heat transfer experiments with inclined hot-wire[J]. Journal of Fluid Mechanics, 1967, 28(1): 153. [10] ZIEIMINSKI K F, SPRUIELL J E. Mathematical model of the crystalline fiber-forming polymers[J]. Synthetic Fiber, 1986, 4: 32. [11] UYTTENDAELE A J, SHAMBAUGH R L. Melt blowing: general equation development and experimental verification[J]. AICHE Journal, 1990, 36: 175. [12] VISHAL B S, SHAMBAUGH R L. On-line determination of diameter and temperature during melt blowing of polypropylene[J]. Industrial Engineering Chemistry Research, 1998, 37: 1799. Simulation and verification of fiber diameter re-increasing in melt blowing process XIE Sheng, HAN Wanli (College of Material and Textile Engineering, Jiaxing University, Jiaxing, Zhejiang 314000, China) In order to directly express the attenuation effect of the air on the fiber in the melt blowing process, the fiber motion in the melt blowing was numerically simulated. Firstly, the fiber in the melt blowing was regarded as beads which connected by Maxwell elements. Then, given air velocity and air temperature were applied to the fiber model. The information such as fiber velocity and fiber diameter in the melt blowing was predicted by this simulation via Lagrange method. The simulation results showed that in the process that the fiber is far away from the spinneret, the air flow force applied on the fiber gradually weakened as the air velocity and air temperature gradually decreased. The fiber retracts under viscoelastic force when the air flow force was less than the viscoelastic force of the fiber, which macroscopically shows the fiber diameter re-increasing. Finally, the fiber diameters were off-line measured under certain experimental conditions, and the result also indicates the fiber diameter re-increasing phenomenon in melt blowing process. melt blowing; fiber path; motion simulation; fiber diameter 10.13475/j.fzxb.20160500505 2016-05-04 2016-11-04 国家自然科学基金资助项目(51506075) 谢胜(1986—),男,讲师,博士。主要研究方向为非织造纤维成型。E-mail:xiesheng212@163.com。 TS 174.1 A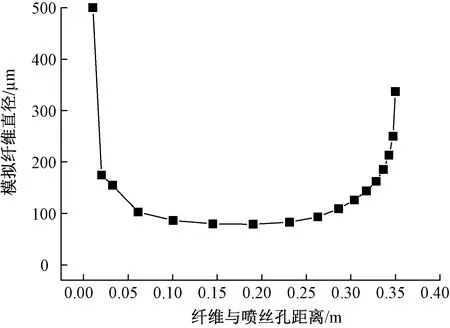
3 结 论

