航空发动机机匣钣金成形及屈服准则

杨俊刚，王 云，郑学著，李又春

(1.南昌航空大学 飞行器工程学院，南昌 330063；2.中国南方航空工业(集团)有限公司，湖南 株洲 412000)

航空发动机机匣钣金成形及屈服准则

杨俊刚1，王 云1，郑学著2，李又春2

(1.南昌航空大学 飞行器工程学院，南昌 330063；2.中国南方航空工业(集团)有限公司，湖南 株洲 412000)

钣金机匣作为航空发动机的主要构成零部件，其结构复杂、材料难于成形，且成形后内部存在不同程度的残余应力，随着计算机的发展，数值模拟成为辅助板料成形研究的主要手段，屈服准则是数值模拟的基础。本文对航空发动机机匣钣金成形性能做以叙述，对各向同性材料屈服准则、各向异性材料屈服准则、先进的各向异性材料屈服准则进行归纳，提出屈服准则应以屈服轨迹、单轴屈服应力、塑性各向异性参数等为选择依据，并提出未来屈服准则可沿新的屈服准则、描述非线性加载情况下的屈服轨迹、创新实验研究方法等方向发展。

航空发动机；机匣；板金成形；数值模拟；屈服准则

0 引言

钣金成形[1]是利用金属在固体状态下的塑性，通过模具以及外力作用而制成零件的一种加工方法。钣金成形加工是金属加工中极其重要的工艺，主要因为该方法生产效率高、原材料消耗少，而且可以有效地改善材料的组织和力学性能，因而在现代工业上得到了极为广泛的应用，特别是在宇航航空、汽车机车、电机电器、日用五金、食品包装等工业部门，钣金塑性成形都是必不可少的主要加工方法。钣金加工中的主要问题和困难，大部分来自于成形方面；因此，在国内外对于如何评价和提高钣金本身的成形性能，如何选用所需要的钣金以及充分利用其成形性能等问题，已成为钣金供货者和加工者十分关心的问题[2]。

随着现代工业的迅速发展，板料成形越来越复杂，传统加工过程的工艺分析以及模具设计制造主要凭借设计者的经验。为了避免成形缺陷的出现，他们往往采用不断地试模、修正的方法，这就必然造成了设计周期长，资源浪费等一系列阻碍发展的问题[3]。随着计算机应用技术的飞速发展，数值模拟成为辅助板料成形研究的主要手段，这样不但可降低试模的成本，而且可以大大地缩短研究、生产周期；但在数值模拟的过程中，模拟精度一直制约着金属板料成形研究的发展。若要提高模拟精度，使数值模拟接近实际的成形过程，就必须准确研究板料的本构关系。在本构关系的研究中，准确地描述板料的屈服行为对研究本构关系有着十分重要的作用，屈服准则的选取不当直接导致模拟结果的失真甚至错误。因此，屈服准则的研究成为金属板料成形行为的关键问题。本文针对金属板料成形性能的概念，数值模拟过程中屈服准则的发展，以及屈服准则的选择进行介绍。

1 航空发动机机匣板金成形概述

金属变形包含着两个明显不同的范畴，即弹性与塑性。金属成形必须在塑性范围内进行，才可以得到永久变形，航空发动机机匣钣金成形必须超过弹性极限，但不应超过缩颈阶段，即塑变量应控制在均匀塑变范围内。因为超过缩颈阶段，特别是出现局部缩颈后纵然可以得到所要求的形状，但在后续成型工序及使用中很容易导致破坏，因此，在压力成形研究中必须研究不发生变形开裂所允许的最大变形量。航空发动机机匣钣金成形的方式很多，通常可用膨胀、拉延、伸长类翻边、弯曲变形等基本变形来表征，为了更好地分析板料对各种成形方式的适应能力，在此引入了钣金成形性能，即拉伸性能、胀形性能、翻边性能、弯曲性能以及复合成形性能等。

航空发动机机匣钣金成形性能可简单地定义为：金属板料通过塑性变形改变形状的能力。钣金基本力学性能可采用拉伸试验测量，通过测量得到两类不同的力学性能：一是强度特性，例如屈服强度、抗拉强度；二是延伸性，即断后伸长率，断面收缩率。钣金成形性能的评价包括抗变形能力的测量(强度)和断裂前拉伸变形程度的测定(延伸性)，然而，要弄清航空发动机机匣钣金成形性能测量的重点是预测和测量断裂之前的变形能力，即不发生开裂所允许的最大变形量。

2 钣金塑性变形行为屈服准则的发展

近几十年来，屈服准则的理论研究得到很大的发展，在数值模拟之前首先要选择合适的屈服准则。因此，必须对各种屈服准则的使用条件以及缺陷有清晰的认识。国外对屈服准则的研究非常重视，但国内对屈服准则的研究并不多[4]。因此，在此有必要对各类屈服准则进行归类分析，特别是对在发展过程中各种屈服准则的使用条件及其缺陷进行整体评估。

2.1 各向同性材料的屈服准则

一般情况下，屈服准则可以用两种不同的方式来定义：一种是假设某些物理量(如能量、应力等)达到某一临界值时发生塑性屈服；另一种是通过解析函数来近似表征实验所得数据。对于各向同性材料，最早用的的是Tresca屈服准则以及Huber-von Mises屈服准则。人们习惯称Tresca屈服准则(图1)为最大剪应力准则，称Mises屈服准则(图2)为能量准则。

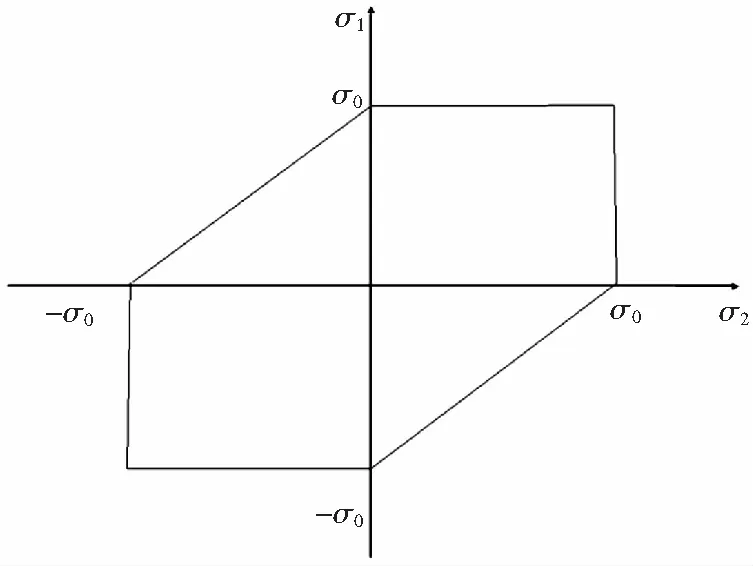
图1 平面应力状态下Tresca屈服准则图Fig.1 Tresca yield criterion under plane stress condition

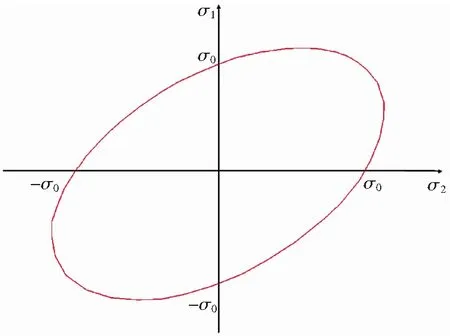
图2 平面应力状态下von Mises屈服准则图Fig.2 Von Mises yield criterion under plane stress condition

1864年，Tresca最早提出的屈服准则是根据实验结果提出的。其认为，是剪应力作用下的晶界滑移引起的塑性应变。根据此屈服准则，当最大剪应力τmax达到临界值时，材料发生塑性屈服。Huber-von Mises屈服准则最早由Huber和von Mises独立提出，Hencky后来对其进行了发展，该屈服准则是在假设静水压力并不影响材料的塑性屈服的基础上提出的，其认为，只用弹性畸变能影响材料从弹性向塑性的转变。该准则可以表述为：当弹性畸变能(也称形状变化能)达到某一与应力状态无关的临界值时，材料从弹性状态转变为塑性状态。也就是发生屈服。本节仅针对典型的各向同性材料的屈服准则进行介绍，更多的各向同性屈服准则，可以参见Zyczkowski[5]和Yu[6]的综述。

2.2 各向异性材料的屈服准则

随着新材料、新工艺的发展，在板料的加工过程中经过多次辊轧和热处理，通常会呈现出明显的各向异性，也就是说内部各个方向的晶粒状态和组织不同，在不同的方向上呈现不同的力学特性，这对板料的塑性成形行为有显著的影响，因此，要提高数值模拟的精度，就必须考虑各向异性对板料成形的影响。在拉深成形的过程中，凸缘出现制耳、拉深直壁出现断裂等现象。对于各向同性金属材料，著名的Mises准则足以描述其屈服行为，但是，为了描述各向异性，则需要对经典的Mises准则进行一定的修正。可以引进一定的参数，但这些参数需要经过试验数据来进行确定。

最早被用于各向异性材料的屈服准则，是由von Mises提出的，其表达式为二次函数形式。最初是用来描述单晶体材料的各向异性塑性变形行为，后来也被用于多晶体材料。1948年，Hill提出了一个各向异性的屈服准则，即Hill48屈服准则，该准则假设材料具有3个相互垂直的各向异性对称面。Hill48屈服准则的优点在于其基本假设很容易理解，屈服函数中的参数有直接的物理意义，在实践中得到了广泛的应用。另外，对于三维问题，该屈服准则仍然具有简单的表达式，并且只需要数目较少的力学参数即可确定屈服准则的表达式。但是Hill48屈服准则不能描述“异常屈服”现象，即该准则无法描述的材料，如铝合金，只能用于在轴对称拉深过程中形成4个“制耳”的材料。 针对二次式的屈服准则不能描述如铝合金等材料的塑性变形行为，Hill在1979年提出了Hill79屈服准则，可以描述“异常屈服行为”的材料，即材料。并且可以得到相关联的流动准则和等效应变的解析式。但由于该函数不含剪应力，只适合应面内各向同性的情况，这限制了其应用，另外，该准则的非凸性会导致屈服表面无限增大。针对Hill79屈服准则只有当主应力的方向与各向异性主轴重合时才能使用，1990年，Hill提出了Hill90屈服准则，该准则可以同时描述“一阶异常屈服行为”和“二阶异常屈服行为”，并且可以很好地描述面内单轴屈服应力和各向异性系数的变化。但是该屈服准则的函数形式比较复杂，需要较长的计算时间。虽然，以上屈服准则的应用范围不断扩大，但依然不能描述某些材料出现的“异常情况”，即板料在不同方向的单向拉伸屈服应力相近而各向异性差异大。为此，1993年，Hill提出了Hill93屈服准则，该准则可以描述上“异常情况”，但它只有在应力主轴和各向异性主轴平行的情况下才能使用，由于存在上述缺点，该屈服准则的的使用还是受到一定的限制。

1972年，Hosford再次提出了Hershey的模型，并用其建立了一个各向异性屈服准则。Barlat等和Banabic等以及其他研究人员提出了更多的扩展形式。1979年Hosford独立提出了Hosford1979屈服准则，该准则可以认为是Hill1979屈服准则的特例。该准则的主要优点在于，通过拟合的方法确定指数a，可以较好地接近Bishop-Hill理论以及实验结果得到的屈服轨迹。1989年Barlat和Lian提出了著名的Barlat-Lian1989屈服准则[7]。该准则能够更合理地描述有较强织构各向异性金属板料的屈服行为。但其无法同时反映面内不同方向上单向屈服应力及各向异性系数的变化，尽管该准则有其局限性，Barlat-Lian1989屈服准则仍然在金属板材的数值模拟过程中经常使用。1991年，Barlat将其屈服准则扩展到三维，为了消除Barlat-Lian1989屈服准的缺点，Barlat提出了一个通用的六参数Barlat1991屈服准则，该准则具有通用和灵活的优点，其预测的屈服面和通过晶体塑性理论计算的结果吻合很好，非常易于在有限元程序中实现，可以很好地预测板平面内不同方向上的单向屈服应力和各向异性系数。但该准则流动法则复杂，不便于使用。大量的实验研究表明，铝合金的塑性变形行为很难用上述屈服准则来描述，在20世纪90年代初，多个学者对该问题开展了研究。为了提高屈服准则的性能，1996年，Barlat等提出了一个1994年屈服准则的通用表达式，也就是Barlat1996屈服准则，利用该准则进行圆筒形件的拉深模拟，可以很好地预测实验中观察到的制耳现象，所计算的屈服面也与Bishop-Hill理论结果和实验结果吻合很好。但该准则中等效应力的导数难以解析确定，因此该模型在数值模拟程序中使用受到限制以及屈服函数的外凸特性无法保证。1993年，Karafills和Boyce[8]针对利用加权法将von Mise和Tresca屈服准则结合到一起，同时利用一个线性转换以实现从各向同性到各向异性的转换。Karafills-Boyce屈服准则预测的屈服面，与实验结果比较吻合，该屈服准则只采用单向拉伸实验来确定材料参数，从数学角度来看Karafills-Boyce屈服准则既简洁又严谨，但该准则转换矩阵的确定步骤比较复杂需要采用数值解法。

2.3 先进的各向异性屈服准则

随着汽车制造业和航空工业中的飞速发展，人们开始研发新的合金钢和具有更好性能的铝合金，同时对镁合金和超塑性合金的使用更有兴趣。从2000年开始，为了更好地描述这些材料的各向异性行为，激发了对屈服准则的相关研究。涌现出一些先进的各向异性屈服准则。

为了解决Barlat1994和Barlat1994屈服准则的缺点，同时保证其灵活的特点，Barlat在2000年提出了专用于平面应力状态的新模型，并通过对两个不同的各向同性屈服准则分别进行转换，提出Barlat-18p屈服准则，该准则已嵌入LS/Dyna商业软件，其能预测杯形件拉深过程中出现6个和8个制耳的情况。但缺点在于需要采用晶体塑性模型来确定部分参数。

GERTETA团队开发一个能够准确描述由织构计算预测的屈服面。在Hershey所提出的各向同性公式的基础上，通过在模型上增加权重因子，提出了Banabic-Balan-Comsa(BBC)屈服准则，BBC2005屈服准则已经集成到AutoForm4.1商业有限元软件中。

为了在各向同性屈服准则中引入正交各向异性，Cazacu和Barlat基于张量函数理论提出了另一种方法，通过将各向同性屈服准则中的应力偏张量不变量换成各向异性的表达式得到了Cazacu-Barlat屈服准则，该准则的优点在于能够准确地描述镁合金和钛合金特有的拉/压异性变形行为。

利用实验中确定的屈服点，Verter等应用bezier插值得到了第一象限内的屈服轨迹，并提出了Verter屈服准则，该准则采用多个参数可保证好的灵活性，缺点是其表达形式复杂，该准则已被集成到PAMSTAMP商用软件中。

Hill在1950年提出一个用于平面应力状态的多项式形式的各向异性屈服准则，Gotoh利用这种思想，成功提出了一个4阶多项式形式的屈服准则，在Hill思想的影响下，还出现了一类新的多项式形式的屈服准则。该类屈服准则容易扩展到三维应力状态，系数多，灵活性好。但是不是所有的公式都满足外凸性，因此一些系数的变换范围需要限定。

3 屈服准则的选择

目前，屈服准则琳琅满目，在一定程度上造成了使用中的混乱，屈服准则的选择关系到数值模拟的正确与可靠，是缩短设计周期的必要前提。因此，在选用之前，需要对屈服准则做出判断。我们需要考虑到所选用的屈服准则对于屈服轨迹、单轴屈服应力、塑性各向异性参数的预测精度是否满足要求。屈服准则其中有一重要作用就是为了嵌入到数值模拟的过程中，因此必须考虑计算效率以及是否易于集成到数值模拟程序中，虽然现在已有相应的屈服准则嵌入到商业软件中，但是或多或少都还存在着模拟精度的问题。随着新材料的不断出现，屈服准则是选择必须考虑其通用性，以及考虑到屈服准则所涉及到的力学性能参数，这些力学参数必须通过实验来获取，因此就需要充分考虑获得力学性能参数所用实验的难易程度。本节针对屈服准则选择的主要面临的问题做以叙述，然而还有其他方面的问题还需要我们借鉴，例如屈服准则是否使用方便、在学术界以及工业届的接受程度等。

4 展望

通过本文对屈服准则的叙述，从各向同性屈服准则的提出，重点到各向异性屈服准则的发展，以及现在的先进的屈服准则的研究。屈服准则的研究已经发生了很大的变化。先进的屈服准则可以准确描述各向异性材料的变形行为。一方面，可以同时描述单轴屈服应力和各向异性系数的变化，另一方面，可以描述一阶和二阶的异常屈服行为。而且，屈服准则还可以推广到三维应力状态，解决更多的工程实际问题。未来该领域的主要研究方向可以集中到以下方面：

1)开发新的能够描述特殊性质的模型的屈服准则，随着新型材料(超塑性材料和记忆性材料等)不断出现，现有的屈服准则不足以描述其屈服行为，因此需要建立新的屈服准则。

2)通过考虑屈服方程中系数的变化，描述非线性加载情况下的屈服轨迹。

3)创新实验研究方法，目前对于屈服准则实验研究的方法主要集中于单向拉伸实验、圆板胀形、厚度方向压缩等基本实验及其组合，仅能反应单拉点、等双拉点、平面应变的特性的变形情况，为了表达板料的真实变形情况，必须创新实验方法，以满足要求。

[1] 吴建军,周维贤. 板料成形性基础理论[M]. 西安:西北工业大学出版社,2010:1-9.

[2] 梁炳文,陈孝戴,王志恒. 板金成形性能[M]. 北京:机械工业出版社,1999:3-19.

[3] 冯兰,蔡英文,何丹农,等. 金属板料成形数值模拟的研究现状[J]. 塑性工程学报,2004,11(6):1-6.

[4] 史艳莉,吴建军. 各向异性屈服准则的发展及应用[J]. 锻压技术,2006,31(1):99-103.

[5] Zyczkowski M. Combined loadings in the theory of plasticity[M]. PWN-Polish Scientific Publishers,1981:89-93.

[6] Yu M H. Advances in strength theories for materials under complex stress state in the 20th century[J]. Applied Mechanics Reviews,2002,55(3):198-218.

[7] Barlat F, Lian K. Plastic behaviour and stretchability of sheet metals. Part I A yield function for orthotropic sheet under plane stress conditions[J]. International Journal of Plasticity,1989,5(1):51-66.

[8] Karafillis A P, Boyce M C. A general anisotropic yield criterion using bounds and a transformation weighting tensor[J]. Journal of the Mechanics and Physics of Solids,1993,41(12):1859-1886.

Forming and Yield Criteria of Sheet Metals for Aero-engine Casings

YANG Jun-gang1，WANG Yun1，ZHENG Xue-zhu2，LI You-chun2

(1.SchoolofAircraftEngineering,NanchangHangkongUniversity,Nanchang330063,China;
2.ChinaSouthernAviationIndustry(Group)Co.,Ltd.,HunanZhuzhou412000,China)

Sheet metal casings, main components of aero-engines, have the following features: complex structure, difficult forming of material and internal residual stress after forming. With the development of computer, numerical simulation has become a main auxiliary means of sheet forming, and yield criterion is the foundation of numerical simulation. The forming performances of sheet metals for aero-engine casings were introduced, yield criteria of isotropic and anisotropic materials were summarized. It is assumed that yield criteria should be based on yield locus, uniaxial yield stress and plastic anisotropy parameters. It is pointed out that the future yield criteria may be developed according to new yield criterion, yield locus under nonlinear loading, and innovative experimental method.

aero-engine; casing; forming of sheet metal; numerical simulation; yield criterion

2016年12月1日

2017年1月20日

杨俊刚(1989年-)，男，硕士研究生，主要从事塑性成形技术等方面的研究。

TG115.5

A

10.3969/j.issn.1673-6214.2017.01.007

1673-6214(2017)01-0033-05