含分布式电源的地区电网无功优化研究

卢海明，郭壮志

（1.广州地铁集团有限公司，广州 510330；2.广东工业大学，广州 510006）

含分布式电源的地区电网无功优化研究

卢海明1，郭壮志2

（1.广州地铁集团有限公司，广州 510330；2.广东工业大学，广州 510006）

分析揭阳地区电网的基本特点和无功配置情况，针对含分布式电源的地区电网无功优化特点，以有功网损最小为目标，提出了基于纵横交叉算法（CSO）的电力系统无功优化方法。CSO算法中首次提出维局部最优概念和纵横交叉双搜索思想，相比其他主流群智能优化算法，CSO算法在解决维数灾问题和收敛精度方面取得了较大突破。算例仿真结果表明，CSO算法寻优质量高、收敛性好，适合求解大规模系统无功优化问题。

无功优化；分布式电源；地区电网；网损；纵横交叉算法

0 引言

传统电网中影响无功优化结果的主要不确定因素是负荷，当分布式电源并网后，其输出功率随分布式电源出力的波动使电网中的不确定因素进一步增多。对于如何利用传统无功电压控制手段与新能源发电相配合，实现含分布式电源的无功电压优化控制，具有重要的现实意义［1］。部分地区电网中存在大量的分布式电源，而且分布式电源存在分布广、供电半径大、负荷峰谷差大等特点，造成电网电压的波动性增大和潮流分布的不合理性［2-4］。因此，解决地区电网中由于分布式小电源导致的无功优化问题，不仅有着重要的现实意义，而且对未来地区智能电网的建设具有指导作用。

含分布式电源的无功优化是一个多变量、多约束、非线性的复杂寻优问题［5］。近年来，人工智能方法在电力系统无功优化问题中得到了广泛应用［6-7］，但随着现代电网规模不断扩大，系统结构日益复杂，传统人工智能方法呈现出早熟现象和容易陷入局部最优的缺点。构建含分布式电源的地区电网无功优化模型，提出纵横交叉算法（CSO）对模型进行求解，采用双交叉搜索机制，能够有效避免维局部最优，从而寻求到全局更优解。实验算例证明了所提模型和算法的有效性。

1 含分布式电源的无功优化模型

电力系统无功优化是指在满足电力系统安全稳定运行的约束条件下，对一系列控制变量，如发电机机端电压、变压器抽头位置、电容器组的投切数目等进行优化调节，从而对系统的无功潮流分布进行合理有效的调控，保证电压在规定范围之内［8-9］。但是，随着分布式电源在地区电网渗透率的提高，要综合考虑含分布式电源的地区电网无功优化数学模型。

1.1 目标函数

以有功网损最小为目标，目标函数为

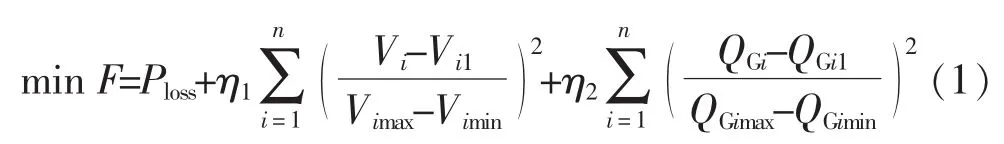
其中：

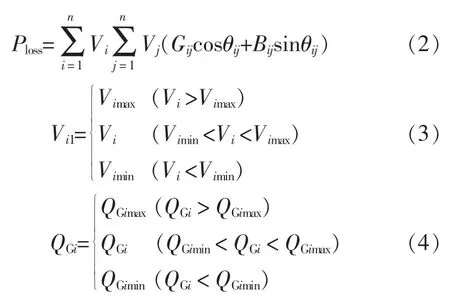
式中：Ploss为有功网损值；η1和η2分别为节点电压和发电机无功出力越限惩罚系数；Vi为节点i的电压值；θij为节点i、j的相位角差；Gij和Bij分别为节点i、j之间的电导和电纳；QGi为发电机无功出力。

1.2 等式约束方程

根据电力系统的运行条件，各节点应满足的等式约束方程（即功率约束方程）为

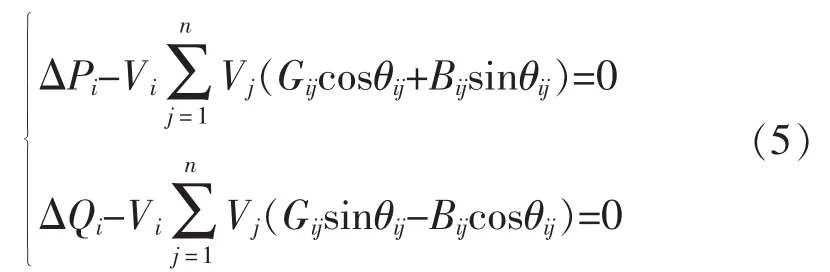
式中：ΔPi为节点i发电机、负荷和分布式电源的有功功率之和；ΔQi为节点i发电机、负荷和分布式电源的无功功率之和。

1.3 不等式约束方程

电力系统运行过程中，除了需要满足等式约束条件，电网运行状态变量以及控制变量还需满足不等式约束。

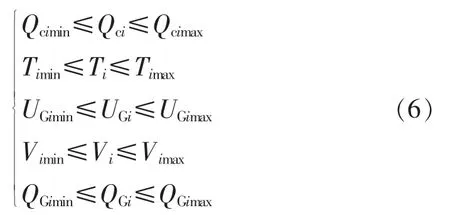
式中：UGi为发电机机端电压；Ti为变压器抽头位置；Qci为电容器组的投切数目；Vi为负荷节点电压；QGi为发电机无功功率。

与常规地区电网不同，当分布式电源接入电网后，为保证电网安全、稳定运行，需要对分布式电源的出力进行一定的控制，使系统的无功潮流分布更加合理。选取分布式电源的有功功率作为控制变量，其约束条件为

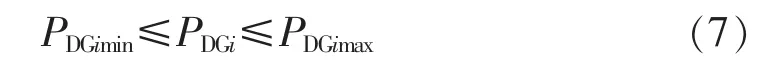
同时，设定分布式电源的功率因数为1。

2 纵横交叉优化算法

纵横交叉算法（Crisscross Optimization Algorithm，CSO）是一种全新的群智能优化随机搜索算法，该算法是受儒家中庸思想和遗传算法启发而创立的，在算法中首次提出了维局部最优概念和纵横交叉双搜索思想。

CSO算法采用一种双交叉搜索机制，包括横向交叉和纵向交叉两种交叉方式，其中横向交叉引入扩展因子增强全局搜索能力，纵向交叉引入维交叉概念，从而避免维局部最优问题。两种交叉算子交替产生中庸解（MShc，MSvc），通过与父代竞争产生的占优解（DShc，DSvc）在种群中相互催化，从而避免早熟问题的同时能够迅速收敛到全局最优。引入竞争机制使两种交叉方式完美地结合起来，增加了算法的全局搜索能力，也加快了算法的收敛速度，对解决连续非线性、非凸性函数优化问题具有很好的适用性。

2.1 横向交叉操作

横向交叉类似遗传算法中的交叉操作，但又有别于遗传算法。遗传算法中交叉操作的作用是父代粒子之间交换种群信息，增强算法寻优能力，而CSO算法的横交叉操作，是在种群中两个不同父代个体粒子相同维之间进行的一种算数交叉。假设父代个体粒子X（i）和X（j）的第d维进行横向交叉，它们的子代繁殖采用如下公式

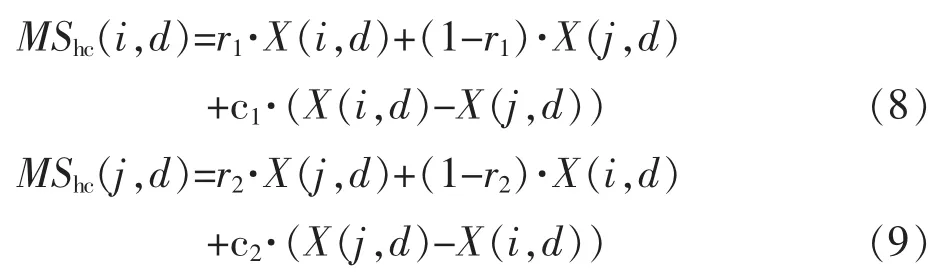
式中：r1，r2为［0，1］之间的随机数；c1，c2为［-1，1］之间平均分布的随机数；X（i，d），X（j，d）分别为父代种群中个体粒子X（i）和X（j）的第d维，MShc（i，d）和MShc（j，d）分别为X（i，d），X（j，d）通过横向交叉产生的第d维子代。

2.2 纵向交叉操作

纵向交叉是种群中一个粒子的两个不同维之间进行的一种算数交叉。这种交叉方法实际是对某个粒子的整维进行变异，促使陷入局部最优的维摆脱出来，增加种群的多样性。假定粒子X（i）的第d1维和第d2维是参与纵向交叉，根据式（10）产生中庸解MSvc（i，d1）。

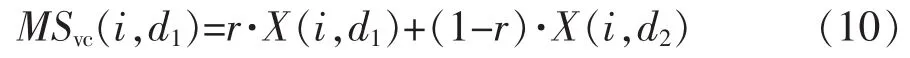
式中：i∈N（1，M）；d1，d2∈N（1，D）；r∈［0，1］，MSvc（i，d1）为父代粒子X（i）的第维d1和第维d2通过纵向交叉操作产生的子代。

在CSO算法中纵向交叉起到十分重要的作用，一旦陷入维局部最优的粒子通过纵向交叉操作摆脱局部最优，在算法迭代过程中，又通过横向交叉操作迅速将新的种群传播到其他粒子，大大加快了整个种群的进化速度和提高了进化的质量。这种特殊的双搜索机制，使得CSO具有良好的鲁棒性，面对高维度、大规模、含较多局部最优点的复杂多模问题时，在全局收敛能力、求解精度和收敛速度等方面对比其他群智能优化算法有较为明显的优势。

3 计算流程

在CSO算法中，解空间中的粒子对应于无功优化的控制变量，包括发电机机端电压UGi、变压器抽头位置Ti、电容器组投切数目Qci以及分布式电源的出力，每个粒子的维数等于控制变量的总数［10］。解空间中的某个粒子可表示为

xi=［UG1，…，UGNG，Qc1，…，QcNc，T1，…，TNT，PDGi，…，PDGNd］T式中：NG、Nc、NT、Nd分别为发电机节点号集合、电容器节点集合、变压器支路集合、分布式电源接入节点号集合，其余变量意义见式（6）。

CSO算法求解无功优化问题的步骤如下：

1）参数设定与种群初始化。输入电力系统参数、种群规模M、迭代次数Maxgen和横向、纵向交叉概率vp、hp，并初始化种群。

2）种群粒子适应度评价。对种群中的每个粒子进行潮流计算，根据式（1）计算该粒子的有功网损，更新个体历史最优pBest和全局最优gBest优。

3）横向交叉。按式（8）、（9）以概率vp对种群粒子执行横向算术交叉，产生的横向中庸解与父代竞争，保留适应度较好的解。

4）纵向交叉。对所有粒子进行归一化处理，按式（10）以概率hp对种群执行纵向交叉操作得出子代，然后反归一化得到纵向中庸解，产生的中庸解与父代比较，保留适应度较好的解。

5）判定是否满足收敛条件或达到最大迭代次数Maxgen，若满足条件则结束迭代过程，输出最优解；否则转到第2）步。

4 实例仿真

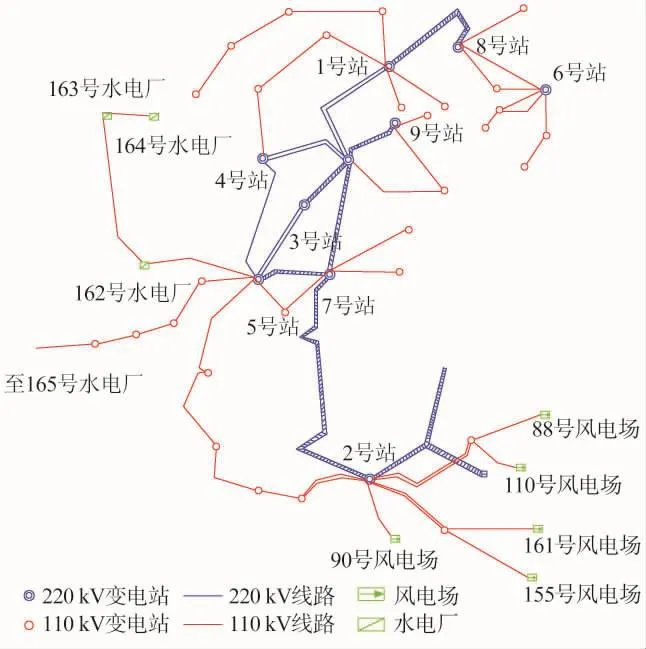
图1 揭阳地区电网部分结构

4.1 揭阳地区电网数据

由于节点较多，图1只描述了揭阳地区电网的一部分。整个揭阳电网共180个节点，包含198条支路，5台风电机组，4台水电机组，78个有载调压变压器，61个无功补偿点，对这些节点进行编号。1为平衡节点，将风机机组作为PV节点，水电机组作为PQ节点接入电网，发电机极端电压变化范围为［0.95，1.1］，有载调压变压器分接头的调节范围取为［-8，8］共17档，本MATLAB电网模型基于该地区电网的夏季最大运行方式，因为该方式下投入的电源容量和负荷最大，等值阻抗最小，同时，负荷较重对地区电网电压水平和无功分布要求更高。因此，选择这种较恶劣的条件进行无功优化研究更能体现CSO算法的有效性。把MATLAB搭建的电网模型与BPA搭建的电网模型对比，潮流分布基本一致。

4.2 仿真结果

为验证提出的CSO算法在大型实际电网中的适用性，以有功网损最小为目标，分别使用 GA、PSO、CSO 3种算法对揭阳地区进行电力系统无功优化，并将优化结果进行对比。设置3种算法的试验参数，PSO算法参数设置为加速因子C1与C2都为2；惯性权重W为0.4；CSO算法参数设置为横向交叉概率为1，纵向交叉概率为0.6；各种算法的种群数均为60；最大迭代次数均为600代。

为避免偶然误差，减少随机性的影响，各算法均独立运行20次，各算法优化后网损的最大值、最小值、平均值以及标准差如表1所示，相应的收敛曲线如图2所示。

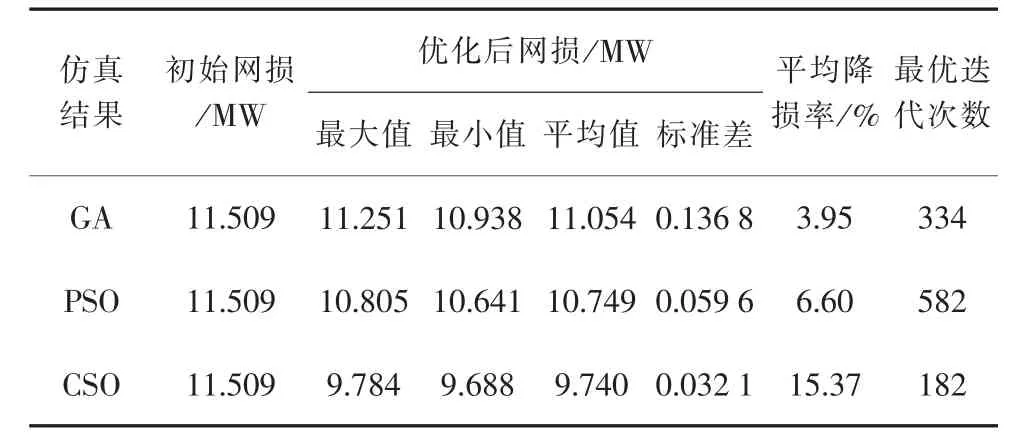
表1 3种算法优化结果对比

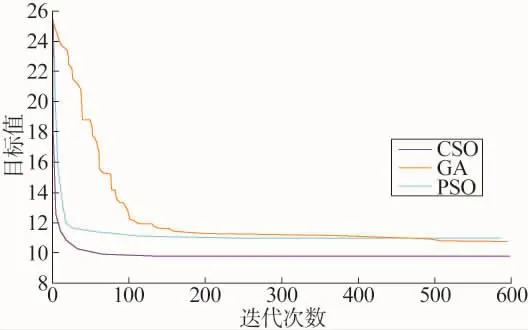
图2 3种算法的收敛特性曲线

由表1可得，CSO算法优化所得最优网损的平均值和标准差均小于其他2种算法，优化网损降低到9.740 MW，比初始网损减少了1.769 WM，这说明在地区电网优化中，该算法的收敛精度和稳定性更好。其次，在降损率方面，CSO算法的平均降损率达到15.37%，几乎是其他算法的2倍多，说明该算法的全局寻优能力更强。

由图2可见，在收敛速度方面，CSO算法也有着显著的优势，虽然PSO算法前期迭代下降的速度还比较快，但收敛精度都不高，而CSO算法迭代到第50代就搜索出全局最优解，收敛精度和收敛速度均优于前2种算法。

揭阳地区电网经过CSO算法优化后各节点电压值如图3所示，所得最优解对应的具体变量数值包括发电机机端电压，电容器组的无功补偿容量和变压器抽头位置（变比），如表2～4所示。

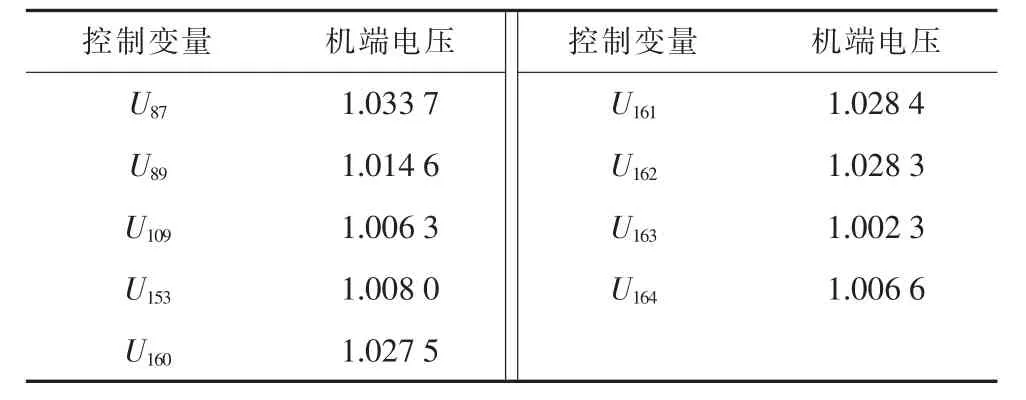
表2 发电机节点电压 pu

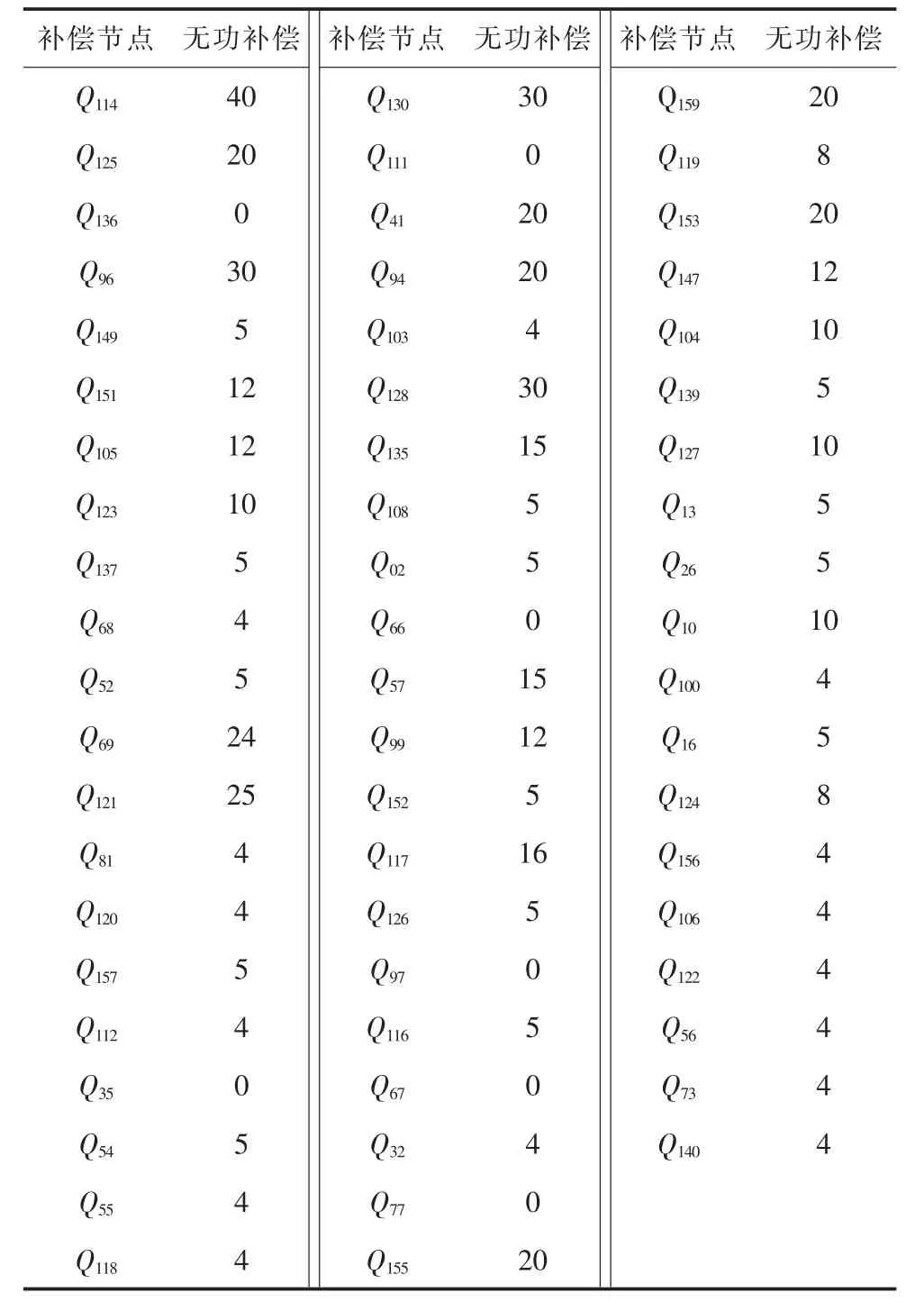
表3 无功补偿 MW

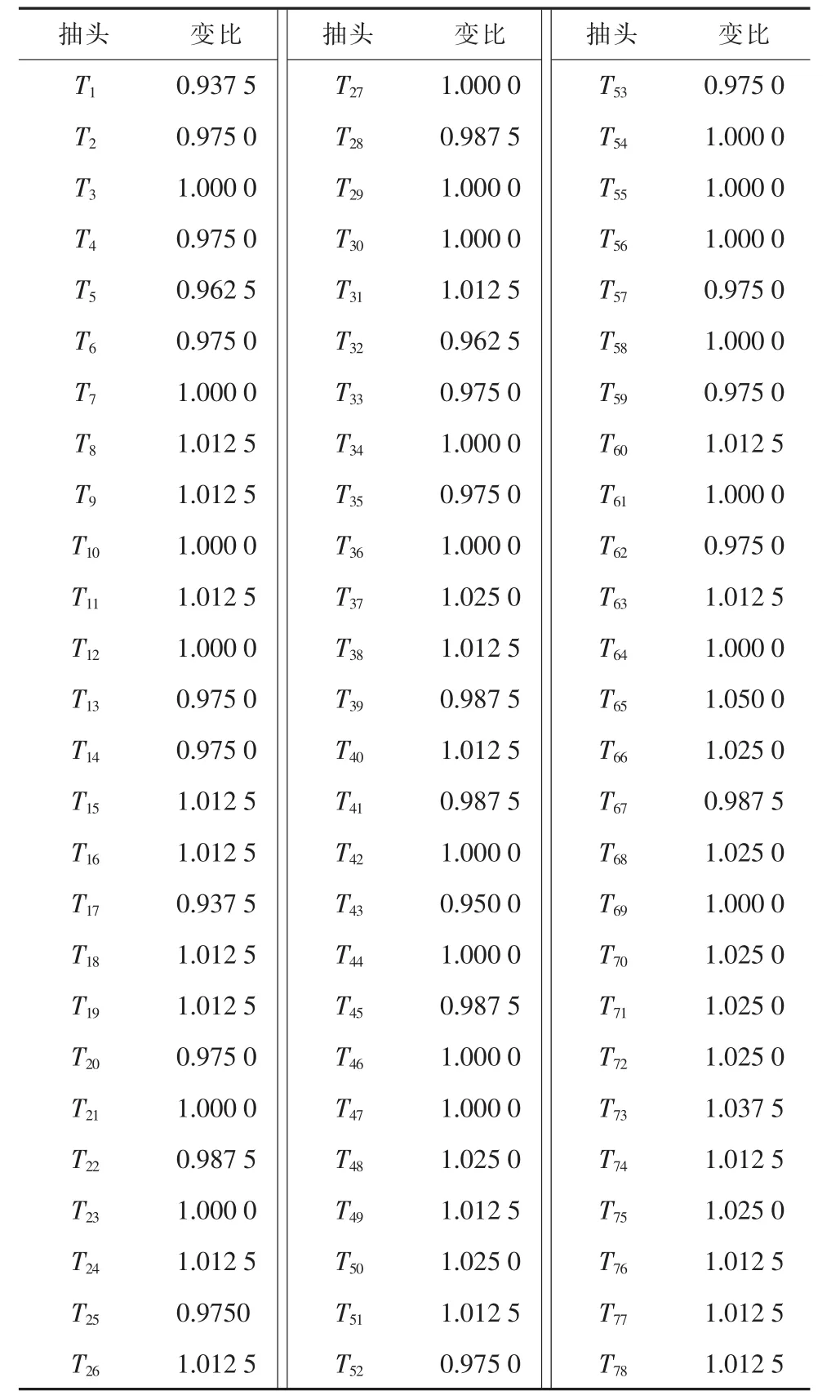
表4 变压器变比 pu

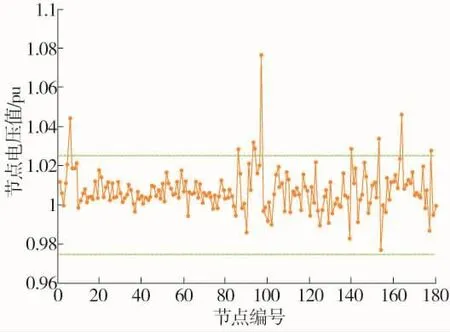
图3 地区电网优化后各节点电压值

从图3可以看出，经过CSO算法优化后的全部节点电压均未越限，绝大部分的负荷节点电压都落在了规定的范围内 （负荷节点电压限制为［0.975，1.025］）。说明利用CSO算法对揭阳电网进行无功优化是合理有效的，达到了预期的效果。

由此可见，CSO算法对于求解电力系统无功优化问题有很大的优势，特别是随着电网规模的增加，其搜索优越性更加明显。

5 结语

以夏季最大运行方式为例，通过调节无功补偿装置的容量、分布式电源的无功出力、变压器抽头的位置对揭阳电网进行了无功优化仿真，并将纵横交叉算法应用到揭阳地区无功优化中，得出了该方式下揭阳电网现场实际无功补偿的容量和变压器抽头的参数表，为地区电网无功优化装置的配置以及电压节点的控制提供了一定的参考。

［1］李智欢，张艳艳，苏寅生，等.南方电网无功电压问题分析［J］.电工电气，2015（8）：18-22.

［2］王旭冉，郭庆来，孙宏斌，等.考虑快速动态无功补偿的二级电压控制［J］.电力系统自动化，2015，39（2）：53-60.

［3］孟安波，岳龙飞，邢林华，等.基于NW小世界的量子进化算法在无功优化中的研究［J］.中国电力，2015，48（1）：107-114.

［4］殷豪，陈春泉，彭显刚，等.分布式电源接入对配电网稳定性的影响研究［J］.东北电力技术，2012，33（10）：6-10.

［5］吕忠，周强，蔡雨昌.含分布式电源的DEIWO算法配电网无功优化［J］.电力系统保护与控制，2015，43（4）：69-73.

［6］孟安波，卢海明，胡函武，等.混合小波包与纵横交叉算法的风电预测神经网络模型［J］.太阳能学报，2015，36（7）：1 645-1 651.

［7］雷敏，杨万里，彭晓波，等.基于改进简化粒子群算法的含DG的配电网无功优化［J］.华北电力大学学报（自然科学版），2015，42（1）：39-44.

［8］颜伟，高峰，王芳，等.考虑区域负荷无功裕度的无功电压优化分区方法［J］.电力系统自动化，2015，39（2）：61-66.

［9］沈天时，刘崇新，岳青，等.基于改进禁忌搜索法的IEEE30节点系统无功优化［J］.电工电气，2015（7）：19-23.

［10］崔挺，孙元章，徐箭，等.基于改进小生境遗传算法的电力系统无功优化［J］.中国电机工程学报，2011，31（19）：43-50.

Reactive Power Optimization of Regional Power Grid with Distributed Generators

LU Haiming1，GUO Zhuangzhi2
（1.Guangzhou Metro Corporation Operation Division，Guangzhou 510310，China；2.Guangdong University of Technology，Guangzhou 510006，China）

Characteristics and the state reactive power configuration of Jieyang power grid are analyzed.According to features of reactive power optimization in district grid with distributed generation， a new kind of algorithm， which is composed of crisscross optimization algorithm （CSO）is proposed.The CSO algorithm includes horizon cross as well as a vertical cross，whose combining enhances the global convergent ability while the introduction of competitive mechanism drives the potential solutions approximate the global optima in an accelerating fashion without sacrificing the convergence speed.The result of an instance shows that the proposed algorithm has advantages of a high quality solution，good convergence and low computational complexity，which is suited to solve large scale reactive power optimization of a power system.

reactive power optimization；distributed generators；district grid；network loss；CSO

TM714.3

A

1007－9904（2017）03－0026－05

2016-10-25

卢海明（1990），男，主要研究方向为城市轨道交通供配电方面；

广东省科技计划项目（2016A010104016）；广东省自然科学基金（S2013040013776）

郭壮志（1984），男，副教授，主要研究方向为电力系统分析与控制、大型水火电力系统联合优化及配电网自动化。