动态载荷识别的自适应延迟逆模型方法

周 盼，蔡龙奇，率志君，李玩幽

（1.哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001；2.中国核动力研究设计院，四川 双流 610213）

动态载荷识别的自适应延迟逆模型方法

周 盼1，蔡龙奇2，率志君1，李玩幽1

（1.哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001；2.中国核动力研究设计院，四川 双流 610213）

为减小载荷识别问题对原系统先验知识的依赖，采用系统的自适应延迟逆模型识别时域载荷。采用自适应算法辨识延迟逆模型，代替了一般识别方法中的系统特性矩阵求逆过程，避免了病态问题。随后将工作状态下的响应作为逆模型的输入，则其输出就是时域载荷的延迟估计。通过对两端简支梁结构进行载荷识别的仿真研究，以及对双层隔振试验台架的试验研究，识别了稳态激励和瞬态激励，验证了该方法的有效性。该方法不需要了解系统的数学模型及参数，因此能够应用于工程实践中。

振动；时域载荷识别；自适应延迟逆模型；时间延迟

0 引 言

近年来，载荷识别的时域方法愈来愈受到国内外学者的关注。目前应用广泛的时域方法主要有反卷积法[1]、SWAT方法[2-3]、卡尔曼滤波器和递归最小二乘法[4-5]、逆系统法[6-7]等方法。反卷积法需要对系统的时域振动特性矩阵进行逆运算，易出现病态问题，影响动态载荷的识别精度。SWAT方法仅适用于具有刚体模态的结构且所求为动态载荷的合力，因此其应用有很大的局限性。卡尔曼滤波器和递归最小二乘法是以系统的状态空间模型为基础的，能够在线识别未知载荷的时间历程，但是该方法需要提前掌握测试噪声及过程噪声的统计特性，否则影响识别精度。

综合各种识别方法的优缺点，本文拟采用逆系统方法识别时域载荷。1995年，魏星原等采用逆系统法识别时域载荷[6]，利用系统的输入输出信息建立自回归滑动平均（ARMA）逆模型，然后求解输入激励，从而将载荷识别的逆问题转化为正问题进行处理，避免了系统特性矩阵求逆过程中可能出现的病态问题。但是由于逆系统的存在条件比较苛刻，这种方法的应用受到一定的限制。1999年，Steltzner和Kammer采用非因果逆向滤波器（inverse structural filter，ISF）识别结构所受载荷的时间历程[7]。通过截断奇异值分解法（TSVD）计算由Markov参数构成的系统特性矩阵的伪逆建立ISF。针对ISF可能会出现不稳定的情况，Allen和Carne以系统的状态空间模型为基础，提出一种改进算法-延迟多步逆向滤波器（delayed，multi-step ISF，DMISF）识别时域载荷[8]。Nordström和Nordberg研究了对位系统（collocated system）、非对位系统（non-collocated system）的载荷识别问题，并采用时间延迟方法将非对位系统的载荷识别病态问题转化为良态问题[9]。现有的逆系统方法多是建立在系统状态空间模型基础上的，需要事先了解系统的先验知识，导致应用受到限制。

鉴于此，本文提出一种基于自适应延迟逆模型的载荷识别的时域方法，摆脱了系统的状态空间模型，不需要掌握系统的数学模型和系统参数。此外，该方法采用自适应算法对延迟逆模型进行辨识，不需要对系统特性矩阵进行逆运算，从而避免了矩阵求逆过程中的病态问题。

1 载荷识别原理

1.1 逆模型辨识

基于系统逆模型的载荷识别时域方法，关键在于建立准确的逆模型使其能够真实反映系统的时域逆特性。本文采用图1所示的有限脉冲响应滤波器（finite impulse response filter，FIR filter）（也称为自适应横向滤波器）[11]模拟单输入单输出（SISO）系统的逆模型。图1所示的自适应横向滤波器的输出信号y（n）为：

其中：L为滤波器阶数，wl为滤波器权值。以白噪声激励（或扫频激励）下的响应信号作为逆模型的输入信号，逆模型输出信号与白噪声激励之差定义为误差信号，自适应滤波器自动调整自身权向量，实现满足某种准则下的最优滤波。机械系统逆向建模的原理图如图2所示。

图3 延迟逆模型建模原理图Fig.3 Schematic diagram of delayed inverse modeling

图2展示了逆向建模的基本思路，但是该逆模型辨识原理并不是对所有系统都适用。对最小相位系统（minimum phase system）（系统的零极点均位于Z平面上单位圆内），采用图2得到的逆是稳定的因果的。但是对非最小相位系统（non-minimum phase system）（系统的零点有的位于Z平面上单位圆外），由于不稳定零点的存在，采用图2建立的逆模型是不稳定的。为解决这一问题，需要引入合适的时间延迟以得到稳定的延迟逆模型[10-11]。延迟逆模型的建模原理如图3所示。

本文采用最小均方误差准则进行逆模型辨识。理论研究表明，当没有噪声干扰时，图3中最小均方误差将为零，逆模型的输出信号就是机械系统白噪声激励的完美匹配，此时这组权向量能够准确反映该机械系统的时域逆特性[12]。采用归一化LMS（Normalized least mean square，NLMS）算法调整自适应滤波器的权向量。图3中延迟逆模型的辨识原理可描述为：

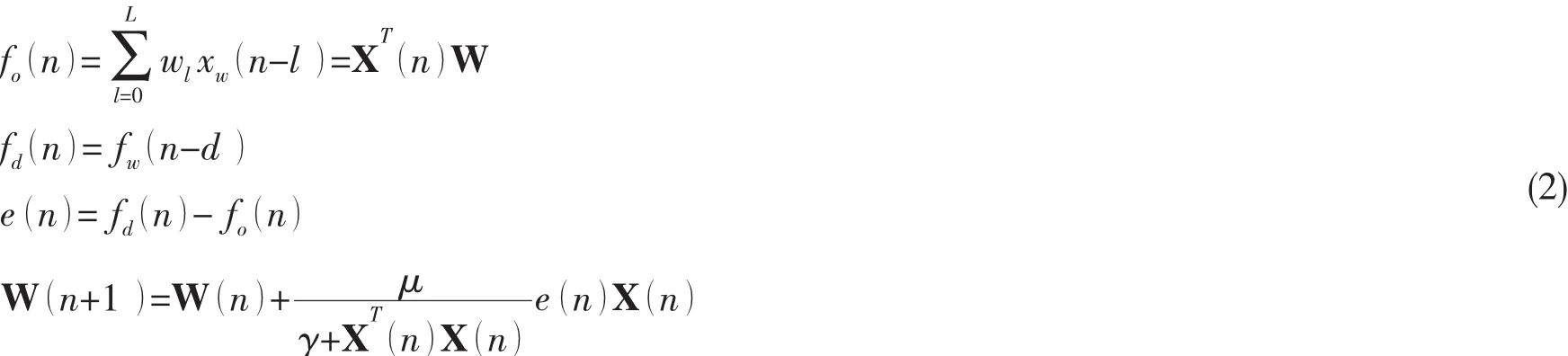
式中：fw（n）、xw（n）分别为n时刻机械系统的白噪声激励和响应。fo（n）为逆模型的输出，fd（n）表示白噪声激励fw（n）延迟时间步长d后的延迟激励。e（n）为延迟激励fd（n）与逆模型输出信号fo（n）之差，为误差信号。其中X（n）=［xw（n）xw（n-1）…xw（n-L）］T、W（n）=［w0（n）w1（n）…wL（n）］T分别为逆模型的输入向量、逆模型权向量。式中L为自适应滤波器的阶数，μ为收敛因子，泄露因子γ∈［0，1］。关于收敛因子的取值范围可参考文献[13]。

当系统响应中存在噪声干扰时，采用图3进行逆模型辨识会导致较大误差，滤波器收敛值会偏离Wiener解。此时系统的延迟逆模型辨识原理应参照图4[14]。首先进行系统辨识，采用自适应滤波器建立正模型，再由系统正模型对延迟逆模型进行自适应建模。图4辨识原理可采用如下公式描述：

图4 有噪声干扰的系统的延迟逆模型辨识原理Fig.4 Delayed inverse modeling of mechanical system with noise disturbance

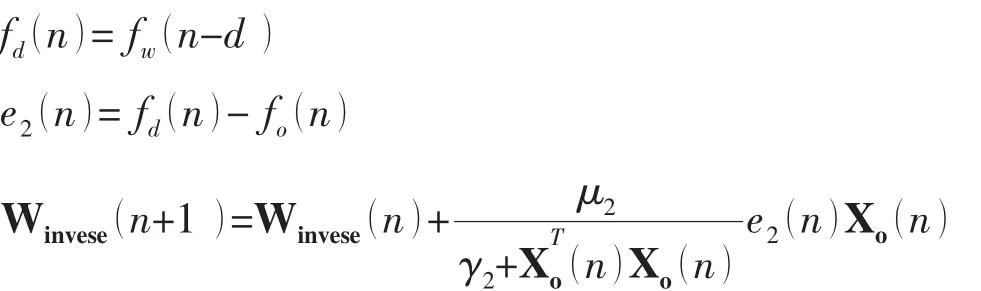
其中：Wforward、Winvese分别为正模型、逆模型权向量，阶数分别为H和L。fw（n）、xa（n）分别为n时刻系统的白噪声激励和包含噪声的响应。

1.2 时域载荷识别

系统的延迟逆模型建模完成后，将系统在实际激励状态下的响应信号作为延迟逆模型的输入，则逆模型的输出就是实际激励的延迟估计。由于延迟逆模型是系统的非因果逆模型，因此载荷识别实际上是采用过去时刻和未来时刻的响应识别当前时刻的激励。

2 载荷识别的仿真研究

2.1 时间延迟对延迟逆模型辨识的影响

时间延迟是延迟逆模型辨识过程中的一个重要参数。时间延迟的引入不仅能够获得稳定的逆系统，同时还可获得更小的均方误差[13]。下面研究时间延迟的选取对延迟逆模型辨识精度的影响。

以两端简支梁为研究对象，长、宽、高分别为0.64 m、0.056 m和0.008 m，密度7 800 kg/m3，杨氏模量2×1011Pa，阻尼因子0.01。截取简支梁的前10阶模态进行动态响应计算。激励力作用于简支梁结构的0.5 m处，加速度响应测点位于0.2 m处，该系统为非最小相位系统。

选取逆模型的自适应滤波器长度分别为50、80、100、150和200，时间延迟的取值范围为[0，200]。图5表示的是最小均方误差与时间延迟的关系。

图5 最小均方误差与时间延迟的关系Fig.5 Relation between least mean square error and time delay

分析图5可知，（1）当自适应滤波器的长度一定时，时间延迟很小（如零延迟）或时间延迟较大（接近滤波器长度），最小均方误差均较大。这是由于时间延迟很小或很大时，逆模型的脉冲响应函数会发生截断，不能准确反映逆系统特性，导致最小均方误差较大。（2）对比自适应滤波器长度为50和200的最小均方误差，长度200时最小均方误差更小，说明滤波器长度越大最小均方误差越小，更能真实模拟系统的逆特性。（3）自适应滤波器的长度取值越大，则最小均方误差较小时对应的时间延迟的可取范围也越大。控制理论中的经验法则是时间延迟等于自适应滤波器长度的一半[13]。

2.2 噪声干扰对载荷识别精度的影响

2.2.1 无噪声干扰情况

以2.1节的简支梁结构为研究对象，对其进行载荷识别的仿真研究。为尽可能准确模拟宽频范围内系统的逆特性，选取白噪声激励（或者扫频激励）以及相应的加速度响应对系统进行逆向建模。仿真中设定时间分辨率0.001 s，自适应滤波器长度200，时间延迟120，收敛系数0.1，泄露因子1。分别识别白噪声激励、单频激励、双频激励和冲击激励，其中冲击激励由半正弦激励表示。单频激励、双频激励以及冲击激励的具体形式分别为：

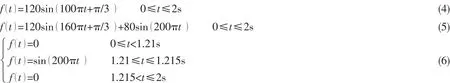
激励力识别结果如图6所示。为保证图清晰可辨，只给出了某段时间内的识别结果。分析图6可知，在无噪声干扰时，该方法能够准确识别出单频激励、双频激励和白噪声激励，冲击激励识别结果与真实冲击也基本吻合。这说明基于延迟逆模型的载荷识别方法能够识别稳态激励和非稳态激励，验证了该方法的可行性。

图6 不同激励形式下激励识别结果Fig.6 Estimated results of operational forces with different excitation types

2.2.2 噪声干扰情况

对于实际工程环境，测试响应中不可避免的存在噪声干扰，有必要研究噪声干扰对该时域方法识别精度的影响。本文采用文献[15-16]中的噪声模型，噪声幅值为响应均方根值的10%，则包含噪声干扰的响应表示为：

其中：nt为数据点数目，x为不包含噪声的真实响应向量，xnoisy为包含噪声的响应向量，η是由均值为0方差为1的正态分布随机数组成的长度为nt的噪声向量。

参照图4，采用白噪声激励及相应的加速度响应（包含噪声干扰）辨识延迟逆模型。仿真中时间分辨率0.001 s，正模型长度为1 000，逆模型长度为200，延迟120。随后利用实际激励下的加速度响应（包含噪声干扰）识别不同形式的时域激励，激励识别结果如图7所示。识别结果表明当响应中包含测试噪声时，激励识别精度较无噪声情况降低，总体趋势与实际激励一致。激励力的识别精度与延迟逆模型的辨识精度息息相关。通过观察冲击激励识别结果，可以看出冲击激励的主峰两侧存在小的旁瓣，这是由于逆模型的不完善性造成的。可采用增加滤波器阶数（相应的改变延迟）和减小收敛系数的方法来获得更加精确的延迟逆模型。

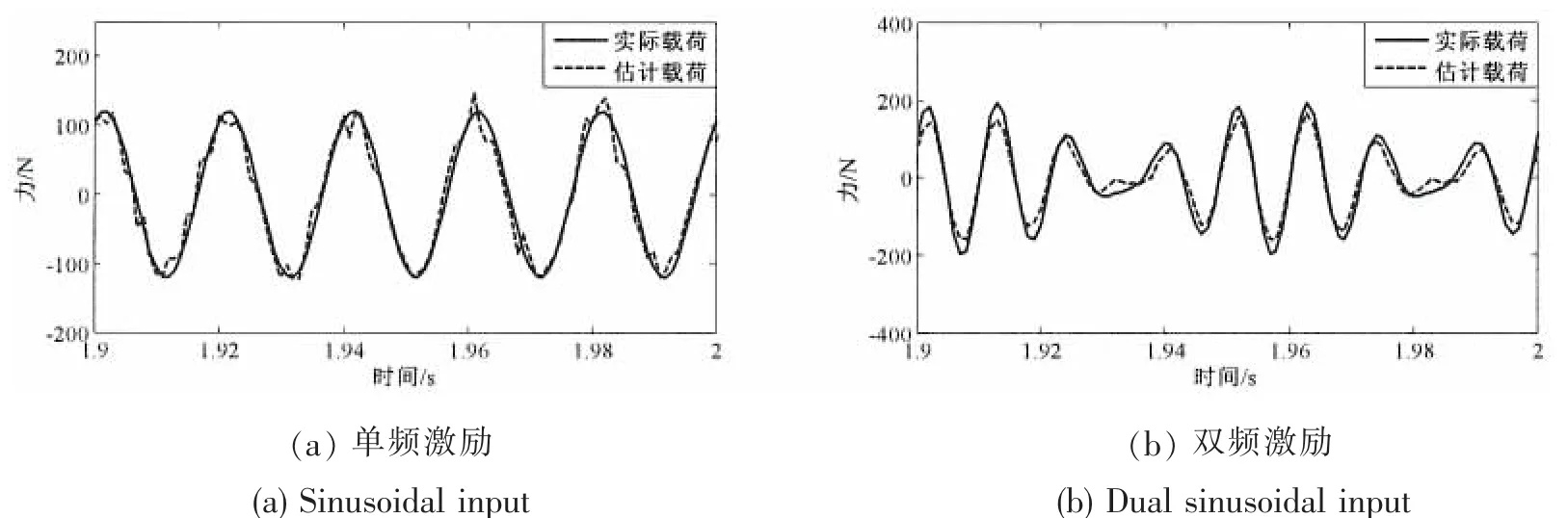
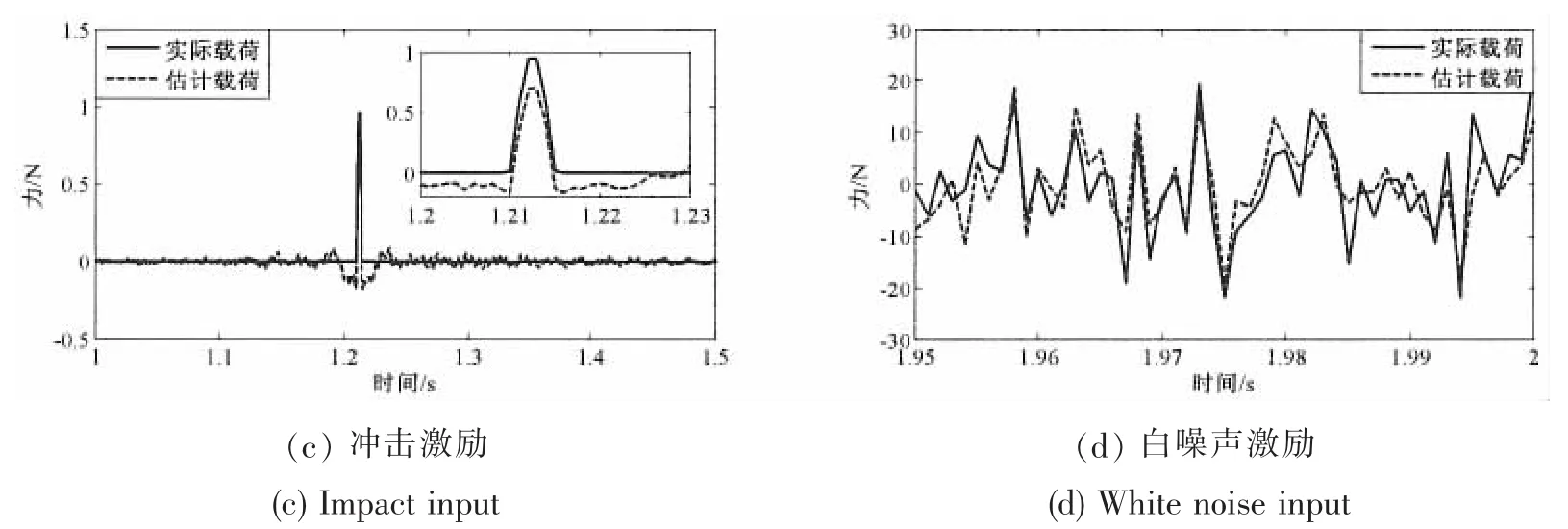
图7 不同激励形式下激励识别结果Fig.7 Estimated results of operational forces with different excitation types

3 载荷识别的试验研究

对双层隔振系统进行载荷识别的试验研究，验证本文中提出的时域识别方法的有效性和可行性。双层隔振系统的试验台架如图8所示。

图8 双层隔振系统试验台架Fig.8 Test bench for two-stage vibration isolation system

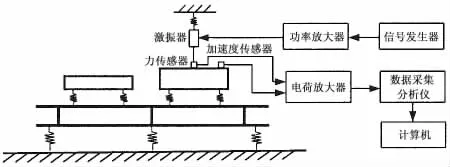
图9 试验装置示意图Fig.9 Schematic diagram of test device

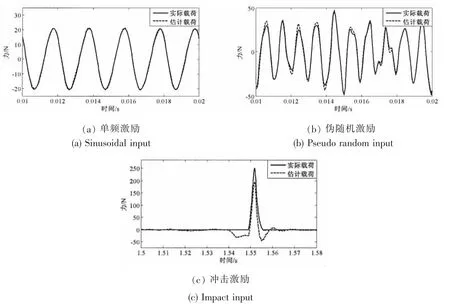
图10 不同激励形式下激励识别结果Fig.10 Estimated results of operational forces with different excitation types

采用弹簧吊装激振器。信号发生器产生信号通过功率放大器输出给激振器，激振器通过激振杆将激振力传递给双层隔振系统，具体作用于上层质量。安装力传感器、加速度传感器分别采集激振力信号和结构的加速度响应。试验装置示意图如图9所示。

逆模型权向量长度为300，时间延迟为160。正弦激励、伪随机激励和冲击激励的识别结果如图10所示。分析图10中识别结果，可知：该方法能够较准确地识别正弦激励和伪随机激励。对于冲击激励，该方法能够准确定位冲击激励的作用时间，但是识别的幅值偏小。

4 结 论

本文采用自适应延迟逆模型识别作用于结构的时域激励，并从仿真、试验两方面验证了该方法的有效性，该方法适用于稳态激励和瞬态激励的识别。在缺少系统先验知识的情况下，该方法具有较大优势。

延迟逆模型的辨识精度对载荷识别有重要影响，而延迟逆模型的建模精度受滤波器阶数及延迟的影响较大。增加滤波器阶数能降低逆模型辨识的均方误差，提高识别精度。在计算时间允许的情况下，可选取较大的滤波器阶数。

本文只给出了单输入单输出系统的载荷识别结果，但该方法同样适用于多输入多输出系统，有待于进一步研究。此外，对噪声干扰强烈的情况，建议首先进行去噪处理，这样能有效提高载荷识别精度，这也是目前较热门的研究方向。

[1]Kazemi M,Hematiyan M R,Ghavami K.An efficient method for dynamic load identification based on structural response [C]//EngOpt 2008-International Conference on Engineering Optimization.Rio de Janeiro,Brazil,2008:1-5.

[2]路敦勇,吴 淼.动态载荷识别的SWAT方法研究[J].振动与冲击,1999,18(4):78-82. Lu Dunyong,Wu Miao.Study on identification of dynamic force using SWAT method[J].Journal of Vibration and Shock, 1999,18(4):78-82.

[3]陈 莲,周海亭.动态载荷识别的计权加速度法[J].噪声与振动控制,2002(3):14-16. Chen Lian,Zhou Haiting.A method of the sum of weighted acceleration in dynamic loads identification[J].Noise and Vibration Control,2002(3):14-16.

[4]Ma C K,Chang J M,Lin D C.Input forces estimation of beam structures by an inverse method[J].Journal of Sound and Vibration,2003,259(2):387-407.

[5]Lin D C.Input estimation for nonlinear systems[J].Inverse Problems in Science and Engineering,2010,18(5):673-689.

[6]魏星原,宋 斌,郑效忠.载荷识别的逆系统方法[J].振动、测试与诊断,1995,15(3):37-43. Wei Xingyuan,Song Bin,Zheng Xiaozhong.A method of inverse system to identify force[J].Journal of Vibration,Measurement&Diagnosis,1995,15(3):37-43.

[7]Steltzner A D.Input force estimation,inverse structural system and the inverse structural filter[D].The University of Wisconsin-Madison,1999.

[8]Allen M S,Carne T G.Delayed,multi-step inverse structural filter for robust force identification[J].Mechanical Systems and Signal Processing,2008,22:1036-1054.

[9]Nordström L J L,Nordberg T P.A time delay method to solve non-collocated input estimation problems[J].Mechanical Systems and Signal Processing,2004,18:1469-1483.

[10]Widrow B.Adaptive inverse control[C]//IFAC Adaptive Systems in Control and Signal Processing.Lund,Sweden,1986.

[11]Widrow B,Plett G L.Adaptive inverse control based on linear and nonlinear adaptive filtering[C].Proceedings of International Workshop on Neural Networks for Identification,Control,Robotics and Signal/Image Processing,1996:30-38.

[12]Widrow B,Stearns S D.Adaptive signal processing[M].Prentice-Hall,Englewood Cliffs,New Jersey,1985.

[13]Haykin S.Adaptive filter theory[M].Prentice Hall,Upper Saddle River,New Jersey,third edition,1996.

[14]Widrow B,Walach E.Adaptive inverse control,reissue edition:A signal processing approach[M].Wiley-IEEE Press, 2007.

[15]Steltzner A D,Kammer D C.Input force estimation using an inverse structural filter[C]//17th International Modal Analysis Conference(IMAC XXVII).Kissimmee,Florida,1999,3727(2):954-960.

[16]Steltzner A D,Kammer D C,Milenkovic P.A time domain method for estimating forces applied to an unrestrained structure[J].Journal of Vibration and Acoustics,2001,123:524-53.

Adaptive delayed inverse model approach for dynamic load reconstruction

ZHOU Pan1,CAI Long-qi2,SHUAI Zhi-jun1,LI Wan-you1
(1.College of Power and Energy Engineering,Harbin Engineering University,Harbin 150001,China; 2.Nuclear Power Institute of China,Shuangliu 610213,China)

In order to relieve the dependence of load estimation upon the prior knowledge of mechanical system,a novel approach is proposed to determine real time force by adopting adaptive delayed inverse model of mechanical system.Delayed inverse model is identified by adaptive algorithm instead of system characteristic matrix inversion in common determination methods and ill-posed problem is avoided consequently. And then according to the inverse model established,the output signal is delay estimation of operational force while operational response is the input of inverse model.Numerical simulation to simply supported beam and experiment to two-stage vibration isolation system were carried out to reconstruct time history of stationary and transient forces,and the feasibility of this method was verified.The proposed method can be applied in practical engineering as it is not necessary to grip the mathematical model and system parameters in advance.

vibration;real time load estimation;adaptive delayed inverse model;time delay

TU312

：Adoi:10.3969/j.issn.1007-7294.2017.05.008

1007-7294（2017）05-0576-08

2016-12-16

国家自然科学基金资助项目（50979016）；中央高校基本科研业务费专项资金项目（HEUCFZ1115）

周 盼（1986-），女，博士，E-mail：zhoupan734@163.com；蔡龙奇（1989-），男，硕士研究生，工程师；李玩幽（1972-），男，教授，博士生导师，E-mail：hrbeu_ripet_lwy@163.com。