追寻数学实验在教学中的自然融入
孙建国
追寻数学实验在教学中的自然融入
孙建国
数学实验应是数学教学过程中的一个环节。否则,数学实验的教学就容易显得突兀。为此,在设计数学实验时,应基于“三个理解”,选准设计的切入点,巧用设计留白。
数学实验;一体化设计;高中数学
随着“互联网+教育”时代的到来,图形计算器、iPad等手持终端已进入校园,基于手持终端的数学实验在教学中的作用也越来越得到认可。为使数学实验在教与学中真正发挥好作用,需要对数学实验与教学进行一体化设计,即把数学实验作为教学过程的一个环节来设计,使数学实验的目的、时机、方法与教学内容和学情等相匹配。笔者选取其中一些教学案例片段,结合本人的实践与思考,谈一谈数学实验与数学教学一体化设计的几点体会。
一、基于“三个理解”,让实验与教学水乳交融
人教社编审章建跃博士曾撰文说过,数学教师要做到“三个理解”,即理解数学,理解学生,理解教学,并强调理解数学是教好数学的前提。[1]因此,对数学实验与数学教学进行一体化设计的时候也应该做到“三个理解”,这样才能让学生“学会”和“会学”。
【案例1】简单线性规划问题的解法探究。
在苏教版高中数学必修5第3.3节 “简单的线性规划问题”第1课时的教学中,一位教师启发学生利用数学实验解决如下问题:
预设的实验步骤如下:
①利用图形计算器画出上述约束条件表示的平面区域,如图1;
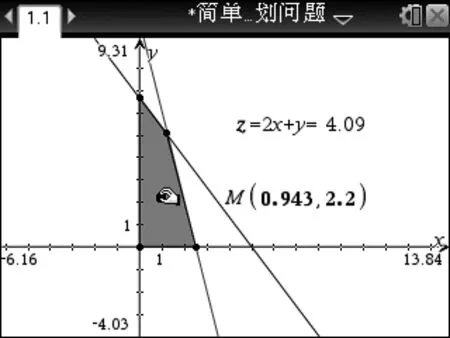
图1
②在平面区域内任取一点M;
③测量点M的坐标,计算z=2x+y的值;
④在平面区域中(包括边界)内拖动点M,通过观察z=2x+y的值的变化来找出最大值。
但在教学过程中的情形如何呢?学生要么找不到最优解,要么找到了却说不出为什么,课堂陷入了尴尬。
这种设计的初衷是引导学生在图形计算器上动手操作,通过反复地“试误”和“比较”来找出最优解,但偏偏在“三个理解”上出了问题。首先,从理解数学来说,让学生在平面区域内用“穷举法”找出使z值最大的点M的方法不可行,因为该平面区域是无穷集,点M的取法不可能穷尽,因而找出最优点M只能凭运气;第二,从理解学生来说,当学生第一次接触有2个变量的函数最值,过去的经验完全用不上时,上述设计中教师没有找准学生思维的盲点;第三,从理解教学来说,教师没有抓住例题解决过程中的新知运用环节,没有为学生形成解决同类问题的“一般观念”而铺设阶梯。
鉴于上述考虑,我觉得可以在一体化设计时删去上述实验中的第④步,而改用以下几个问题来引导学生,效果则可能完全不同。
问题1:请在平面区域内找出一个点,使z=2,并与同学交流。
问题2:大家所找出的点M有什么共同点?
问题3:平面内所有使z=2的点M组成一个什么图形?
问题4:用图形计算器验证,当直线l:2x+y=2向上平移时,其上每一点对应的z=2x+y将如何变化?为什么?
问题5:用图形计算器验证,当直线l:2x+y=2向下平移时,其上每一点对应的z=2x+y将如何变化?为什么?
上述基于“三个理解”的数学实验与教学一体化设计,可以减少学生在数学实验中的盲目性,有效地唤醒学生原有的知识、方法和经验,并以问题串适时地点拨学生,使其按照思维阶梯一步一步找到解决同类问题的方法步骤,形成所谓的“一般观念”。
二、选准切入点,让实验在教学中流光溢彩
笔者在研究过程中,按实验的目的差异把高中数学实验分为验证性实验和发现性实验。其中验证性实验主要指学生为了验证已知结论 (公式、定理、法则和猜想等)而进行的数学实验;发现性实验则是对数学结论的“再发现”过程,它们都是手脑并用、有意义的思维活动。但一些数学实验却存在着可有可无、采点不当的问题。
【案例2】正整数平方和公式的“发现”。
正整数平方和公式的推导是(苏教版)高中数学选修2-2“推理案例赏析”中所录的案例之一。它由以下两部分组成:一是利用归纳推理“发现”公式,二是利用演绎推理证明公式。下面重点讨论公式的发现过程。
课本案例设计的发现过程如下:
设S1(n)=1+2+3+…+n,S2(n)=12+22+32+…+n2
先通过列出下表:
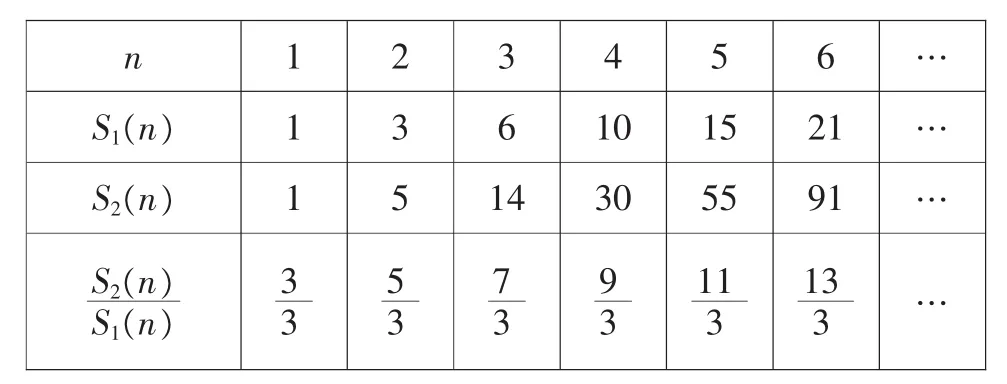
n 111 3 2 3 4 5 6…3 6 10 15 21 …5 14 30 55 91 …5791113 S1(n)S2(n)S2(n)S1(n )333333…
本案例的初衷是让学生欣赏综合运用合情推理和演绎推理解决真实数学问题的过程,培养学生进行数学探索、数学发现的能力,从这个意义上来说,在这个案例中,选择电子表格呈现对比数据使得自然数平方和公式的发现非常直观,这个点选得不错,但其实借助图形计算器或电脑软件,这个公式的发现门槛可以降得更低。
学生已学过函数的概念和一些基本初等函数的图象与性质,不妨启发学生用另一个直观工具——图象来观察“和与项数的关系”。学生可利用图形计算器作出(n,S(n))散点图,并根据图象特征合理猜想函数S(n)的可能类型(如图 2)。接下来,教师可以引导学生进行数学实验与思考。
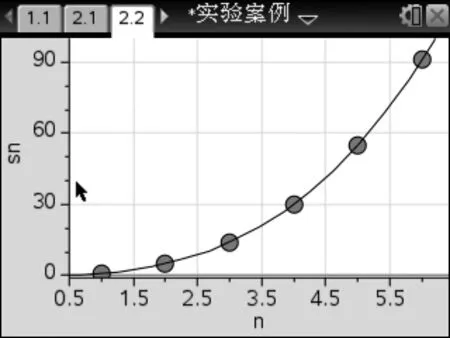
图2
教师:根据散点图中点的分布特征,你想到了什么函数图象?
学生:半条抛物线。
教师:如果(n,S(n))在一条抛物线上,请求出函数解析式Sn=f(n),并用计算器验证其正误。
学生:利用前3个点的坐标可由待定系数法得到:Sn=2.5n2-3.5n+2,但计算发现S4=28,与12+22+ 32+42=30不符。
学生:难道是三次函数?
教师:请求出这个三次函数表达式,并利用计算器验证其正误。
三、巧留设计空白,让实验激发学生创新
我们常常看到,目前课堂教学中的一些数学实验,有的只是由学生播放、演示由教师事先制作的课件,有的则是学生在教师的统一指令下亦步亦趋,这种包办的做法忽视了学生的个体差异,也不能有效激发学生的创造欲。因此在一体化设计时,教师可以注意对实验的方法与步骤留白,让学生在能力范围内自主构思实验的方法和步骤,以提高学生借助工具去解决问题的能力,提升数学核心素养。以下是笔者执教“函数图象的平移和伸缩变换”一课的案例片段。
【案例3】探究函数图象的横向伸缩变换。
教师:刚才我们研究了函数图象的纵向变换规律,请你通过实例研究函数图象的横向伸缩变换。
教师:非常好!请大家测量横向变(窄)宽的比例,然后归纳出一般结论。
学生(边演示边讲):过函数y=f(x)图象上任一点A作y轴的垂线,与函数y=f(kx)的图象交于B点,分别测量A、B的坐标,可发现点B的横坐标是点A横坐标
教师:很好!根据上述实验,我们可以得出什么一般结论?
教师:如何证明上述结论对任何函数和正数k成立呢?
教师:很好。还有其他方法吗?
学生:像横向伸缩变换的证明一样,设A(x,y)是函数图象上任意一点。则,故知点在函数y=f(k·x)图象上,所以将点A的横坐标变为原来的,纵坐标保持不变,即可得点B,考虑到点A的任意性,结论成立。
函数图象的横向伸缩变换是伸缩变换的难点所在。按照传统的教学次序,各版本高中数学教材都不约而同地将此内容安排在学过三角函数的图象、性质之后,并以函数y=Asin(ωx+φ)为例来研究。教学中学生会参照周期的变化,来直观感知横坐标变化的理由。虽然这样设计增加了直观性,但降低了认识的深度。造成部分数学资优生的困惑:伸缩变换的规律对于非周期函数是否适用呢?如果也适用,那么理由是什么?等等。鉴于此,笔者为所教的实验班学生设计了本课,并在高一阶段就让学生来探究函数图象的伸缩变换规律。在本课的教学过程中,对函数图象的纵向伸缩变换的研究是在教师引导、示范下通过数学实验完成的,但在研究横向伸缩变换时,考虑到学生已有了研究函数平移变换、纵向伸缩变换的经历,笔者加大了学生的探究自由度,结论的探究和证明完全交给学生去完成,最终收获了满满的惊喜。学生不仅得出了正确的结论,而且证明方法也简明、正确、严谨。
匈牙利数学家波利亚说过,数学有两个侧面,一方面它是欧几里得式的严谨科学,从这方面看,数学像是一门系统的演绎科学;但另一方面,创造过程中的数学看起来像是一门试验性的归纳科学。因此在教学中引入数学实验的意义是毋庸置疑的。为了让数学实验为课堂提质增效,必须基于 “三个理解”,并为学生预留创新的空间,从而使“发现”触手可及,水到渠成。而这也是全面落实课程目标,更好地发挥数学育人功能的应有之义。
[1]章建跃.理解数学是教好数学的前提[J].数学通报,2015(01).
G633.6
A
1005-6009(2017)27-0012-03
孙建国,江苏省太仓高级中学(江苏太仓,215411)教师,高级教师,苏州市名教师。

