微分进化优化神经网络KUKA机器人逆运动学求解

白文峰, 刘纪阳, 雷宇欣

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)



微分进化优化神经网络KUKA机器人逆运动学求解

白文峰, 刘纪阳, 雷宇欣

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

结合KUKA机器人的正运动学分析，将正运动学求解的结果作为DE-BP优化网络的训练样本，求解了机器人逆运动学问题。

机器人； 微分进化； 神经网络； 逆运动学求解

0 引 言

机械臂运动学研究的是机械臂的运动规律,而非机械臂动作的力和力矩。主要研究内容包括：正运动学求解问题和逆运动学求解问题[1]。机器人运动学正问题，就是根据给定的各关节角度求解出机器人末端执行器在工作空间上的位姿。机器人运动学逆问题是依据机器人末端执行器(手端)在工作空间上的位姿求得各对应关节变量的过程。目前，求解逆运动学的主要方法有：解析法、几何法、迭代法、几何-解析法、符号及数值法[2]。然而，实际应用中不容易得到精准的机器人模型,导致上述方法存在一定不足，如多解、奇异性、收敛速度慢及计算量大等问题。文中采用的神经网络具有很强的非线性映射能力，依靠网络结构就能求得机器人的运动学逆解，而不用考虑机器人有几个自由度[3-5]。考虑到神经网络训练时存在收敛速度慢、迭代次数多等缺点，文中采用微分进化DE算法对BP网络结构参数进行优化，从而快速获得更高精度的逆解。

1 KUKA机器人D-H描述

研究的KUKA工业机器人共有6个自由度，各个关节均可旋转，机器人末端操作手的位置由前3个关节控制，姿态由后3个关节控制。建立KUKA工业机器人的连杆坐标系模型[6-7]如图1所示。

各连杆参数见表1。

θi、di、ai、αi这4个参数称为D-H参数，其中，di、ai、αi是代表机器人结构参数的常量，θi用来控制机器人位姿的关节变量。

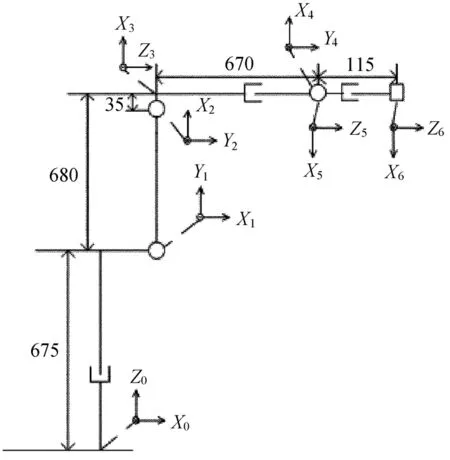
图1 KUKA工业机器人的连杆坐标系

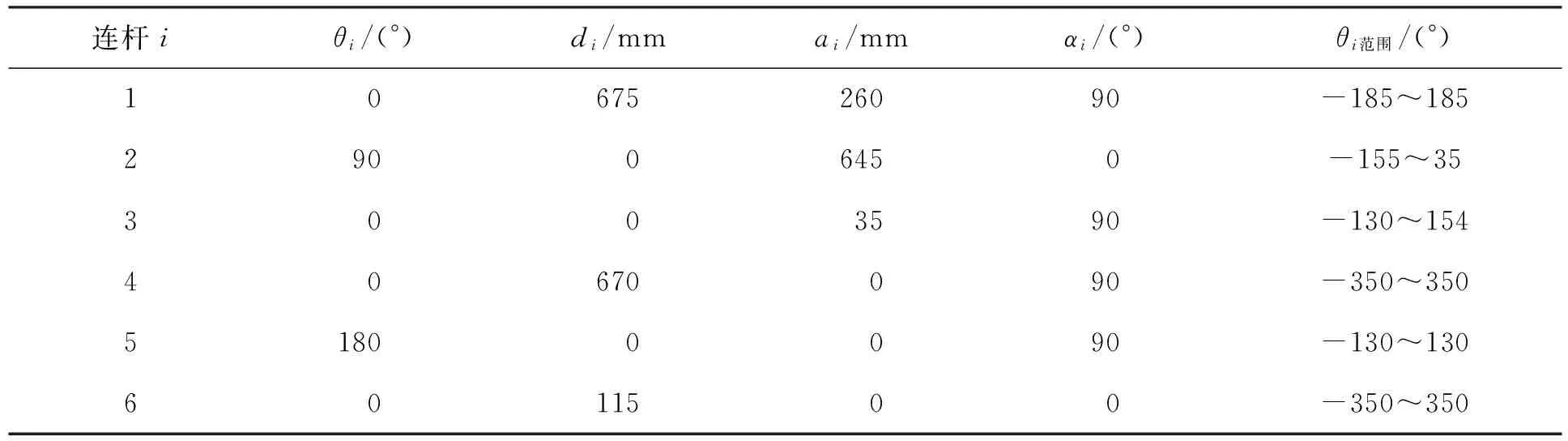
连杆iθi/(°)di/mmai/mmαi/(°)θi范围/(°)1067526090-185～18529006450-155～353003590-130～15440670090-350～35051800090-130～1306011500-350～350

根据表1中各连杆参数和关节变量值，利用刚体运动学理论知识[8]计算出连杆i-1到连杆i的齐次变换矩阵：

i-1Ti=Trans(zi-1,di)Rot(zi-1,θi)Trans(xi,ai)Rot(xi,αi)=

其中，sθi=sinθi,cθi=cosθi,sαi=sinαi,cαi=cosαi。

根据串联刚体间的链式关系，将连杆变换矩阵连乘，可以得到由机器人基准坐标系到末端坐标系的转换关系，即机器人末端(手端)相对于机器人基准坐标系的位姿:

2 DE和BP算法

微分进化(DE)是一种随机优化算法[10]。除了具有强大的全局搜索性能外，还具有鲁棒性好、快速、简单等特点。它的变异算子是由种群中任意选取的多对向量的差值得到的，这是与其它进化算法的不同之处。在非线性问题上，该算法优于其它进化算法。微分进化(DE)的基本操作步骤是：构造矢量参数集，通过杂交、变异和选择得到初始化群体，对种群逐步进化得到最优解。

BP网络主要由三部分构成：输入层、中间层和输出层[11-13]。包含有正向传播和反向传播两个学习过程。主要训练思想是：信息从输入层经中间层而后再经过输出层得到一个实际输出值，若与预期值存在一定偏差，网络就会反向传播，逐一修正各层神经元的权值和阈值。如此不断反复地迭代更新权值和阈值，直到求得实验预期的输出值为止。BP神经网络存在诸多不足，如训练过程中容易陷入局部最优；学习新样本存在遗失原样本的可能；在原始数据信噪比低时存在不收敛的情况。因此,文中运用了DE算法优化BP神经网络参数以避免以上问题，减少了优化过程对种群原始数据的依赖，使得算法的全局搜索能力更加优良。

3 DE-BP算法的实现

采用的BP网络结构如图2所示。

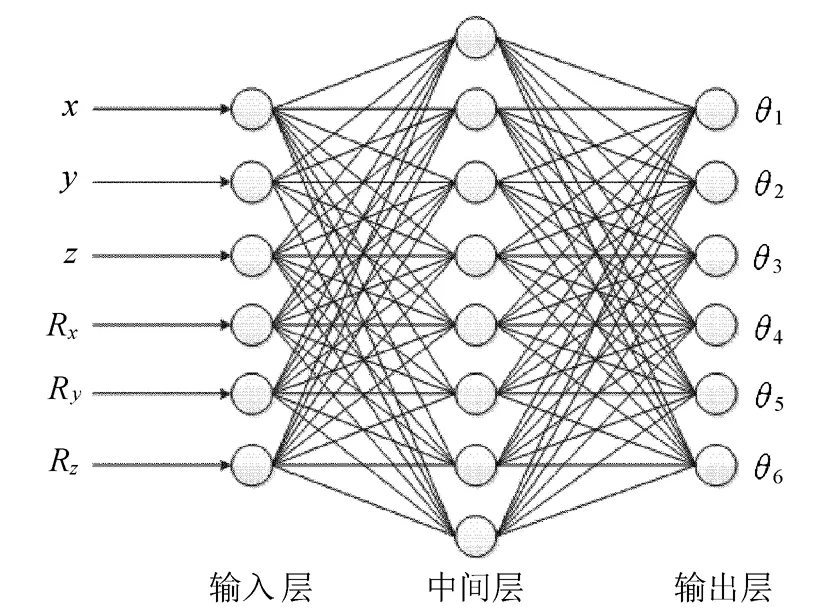
图2 BP神经网络结构

机器人末端的空间位姿P=[x,y,z,Rx,Ry,Rz]作为BP网络的6个输入，中间层有8个隐含结点，BP网络的输出分别是6个关节变量

θ=[θ1,θ2,θ3,θ4,θ5,θ6]

文中用微分进化算法对BP神经网络的阈值和权值进行优化，使下面的适应度函数达到最小值：

式中： yi,j----BP神经网络的实际输出；

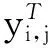
DE优化BP神经网络的工作流程如图3所示。

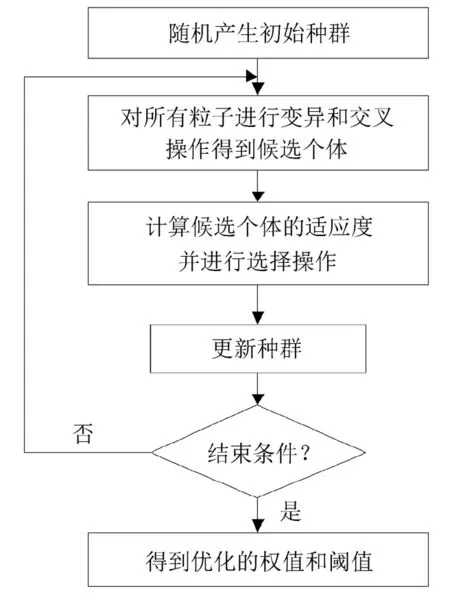
图3 DE优化BP神经网络的过程

1)根据样本数据确定BP神经网络的初始权值和阈值，由这些权值和阈值作为微分进化算法的初始化种群；设定DE算法的种群规模NP=220，变异因子F=0.6，交叉因子CR=0.5，最大迭代次数A=500。

2)采用粒子群杂交、变异的方式求得新一代候选个体；对个体适应度评估，选择最优个体更新原有粒子群。

3)循环迭代直到求出满足条件的阈值和权值，然后替换BP神经网络原有的阈值和权值。

4 仿真分析

仿真实验基于MATLAB的Robotics工具箱和神经网络工具箱对DE-BP神经网络的有效性进行验证。通过式(2)和式(3)计算关节空间{θ1,θ2,θ3,θ4,θ5,θ6}对应的机器人末端执行器位姿矩阵{xi,yi,zi,Rxi,Ryi,Rzi}，从而得到学习样本{xi,yi,zi,Rxi,Ryi,Rzi}→{θ1i,θ2i,θ3i,θ4i,θ5i,θ6i}。网络的输入为机器人位姿矩阵，网络输出为各关节角度。将误差精度等级设为0.001，以θ2为例，对期望输出值与预期输出值进行误差比较试验。

采用同样的训练样本，分别选用标准BP网络和DE-BP网络进行逆运动学求解，仿真得到期望输出和实际输出的误差，如图4和图5所示。

显然，优化后的BP网络误差更符合要求。

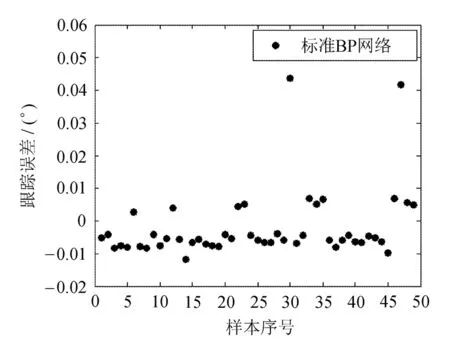
图4 标准BP网络输出误差

图5 DE-BP网络输出误差

5 DE-BP网络的KUKA机器人运动学

根据KUKA机器人的可动范围及各关节角实际参数，可以确定各个关节角的取值范围为：

-180°≤θ1,θ4,θ6≤180°

-120°≤θ3,θ5≤120°

-120°≤θ2≤35°

网络训练成功后，在机器人工作空间随机选取8组测试数据，将待测数据送入网络中，验证结果见表2。

表2 DE-BP网络对KUKA机器人逆解的求解结果

6 结 语

采用微分进化算法优化BP神经网络权值和阈值的方法在一定程度上解决了难以在初始阶段设定BP神经网络权值和阈值难的问题，实现了二者的互补，使得BP神经网络能够较快地求得关节变量的最优解。仿真结果证明，此算法使误差精度基本达到了机器人逆运动学问题求解的要求。

[1] 蔡自兴.机器人学[M].2版.北京：清华大学出版社， 2009.

[2]NikuSB.机器人学导论:分析、系统及应用[M].孙富春，朱纪洪，刘国栋，等,译.北京:电子工业出版社，2004.

[3]KarlikB,AydinS.Animprovedapproachtothesolutionofinversekinematicsproblemsforrobotmanipulators[J].EngineeringApplicationofArtificialIntelligence,2000,13:159-164.

[4] 陈学生,陈在礼,孔民秀,等.基于神经网络的6-SPS并联机器人正运动学精确求解用[J].哈尔滨工业大学学报,2002,34(1):120-124.

[5]MartinetzM,RitterJ,SchultenJ.Three-dimensionalneuralnetforlearningvisuomotorcoordinationofarobotarm[J].IEEETransactionsonNeuralNetworks,1990(1):131-136.

[6] 熊有伦.机器人技术基础[M].2版.武汉：华中理工大学出版社，1997.

[7] 魏厚忠，薛丹，焦立奇，等.基于KUKA6自由度机器人的误差分析与仿真[J].长春工业大学学报：自然科学版，2012,33(3)：328-332.

[8] 王德伦.机械运动微分几何学分析与综合[M].北京:机械工业出版社,2015.

[9] 宋伟刚.机器人学—运动学、动力学与控制[M].北京：科学出版社，2007.

[10] 冯琦，周德云.基于微分进化算法的时间最优路径规划[J].计算机工程与应用，2005，41(12)：74-75，222.

[11] 钟珞，饶文碧，邹承明.人工神经网络及其融合应用技术[M].北京：科学出版社，2007.

[12] 高隽.人工神经网络原理及其仿真实例[M].北京；机械工业出版社，2003.

[13] 葛哲学，孙志强.神经网络理论与MATLABR2007实现[M].北京：电子工业出版社，2007.

Inverse kinematics solution of KUKA robot based on improved differential evolution-neural network

BAI Wenfeng， LIU Jiyang， LEI Yuxin

(School of Electrical & Electronic Engineering, Changchun University of Technology, Changchun 130012， China)

The results from forward kinematics analysis for KUKA robot is taken as the training samples for differential evolution-neural network to solve the inverse kinematics problems.

robot; differential evolution; neural network; inverse kinematics.

2016-08-17

白文峰(1962-)，男，汉族，吉林长春人，长春工业大学教授，硕士，主要从事智能仪器与智能控制方向研究,E-mail:baiwenfeng@ccut.edu.cn.

10.15923/j.cnki.cn22-1382/t.2017.2.11

TP 241.2

A

1674-1374(2017)02-0162-05