超细粉在声场导向管喷流床中的聚团尺寸预测模型

高凯歌，雷玉庄，李海念，周勇



超细粉在声场导向管喷流床中的聚团尺寸预测模型

高凯歌，雷玉庄，李海念，周勇

（四川大学化学工程学院，四川成都 610065）

超细粉的流化性能与聚团尺寸密切相关。通过分析超细粉聚团在声场导向管喷流床中的形成过程，提出了高速射流的剪切作用和聚团间的碰撞作用是决定聚团尺寸的主要原因。在此基础上，结合聚团在射流剪切过程和聚团间碰撞过程中的力平衡分析，建立了声场导向管喷流床中聚团尺寸分布的预测模型；并运用这一模型成功预测了不同射流气速下，超细TiO2颗粒在声场导向管喷流床中的聚团平均直径和聚团尺寸分布。

纳米粒子；声场导向管喷流床；射流剪切作用；聚团间碰撞作用；粒度分布；预测模型

引 言

超细颗粒因具有许多大块物料所不具备的新性质与新效应，在众多领域得到了越来越广泛的应用[1]；流态化技术则由于具有较高的气固接触效率而在超细颗粒的制备和应用方面表现出独特的优越性，所以超细颗粒的流态化越来越受到人们的关注。但超细颗粒因黏附性强，在低气速下流化时，易产生沟流、节涌，难以实现平稳流化[2]。近年来的研究表明，对黏性较小的超细颗粒，通过采用高气速[3-4]、引入外力场[5-8]或添加粗颗粒的方法[9]，可使之形成尺寸较小的聚团，进而以聚团形式实现稳定流化[10]；而对黏性较强的粉体[3, 11]，采用以高速射流为喷动气的导向管喷流床可有效破碎大聚团，若同时在环隙区引入声场[12]，则可进一步改善其在环隙中的流化质量。

无论是在传统流化床还是在引入外力场或添加粗颗粒的流化床中，抑或是在声场导向管喷流床的环隙区，超细颗粒都是以聚团的形式流化，因此，超细颗粒的流化行为与聚团性质和尺寸密切相关。为此，众多研究者对超细颗粒在流化床中的团聚行为进行了研究，并提出了各种聚团尺寸预测模型。这些模型大致可分为两类：力平衡模型[13-15]和能量平衡模型[16-18]，其中力平衡模型建立在更明确的聚团形成机理之上，更易被人们理解和接受。然而已有模型都是针对普通流化床或引入外力场流化床等特定条件下建立的，还没有针对声场导向管喷流床中超细粉聚团尺寸的预测模型；并且已有模型仅能预测聚团尺寸的平均值，而颗粒在实际流化过程中形成的聚团是不均匀的，因此，得到关于聚团尺寸分布的预测模型更为合理。

为此，本文在对超细颗粒在声场导向管喷流床中团聚机理的分析基础上，通过对聚团的受力进行分析，建立了超细粉在声场导向管喷流床中的聚团尺寸分布预测模型，并用平均粒径290 nm的TiO2超细颗粒的实测结果验证了该模型的合理性。

1 模型的建立

1.1 聚团形成过程分析

超细颗粒因粒径小，颗粒间黏附力强，在自然状态下很难以单个粒子分散的状态存在，而是以几微米甚至几十微米的聚团形式存在，这种聚团具有一定的机械强度，被称为自然聚团或一次聚团。由于自然聚团间仍然有较强的黏附力，在外力作用下会进一步发生黏附团聚，形成较大的聚团。在以高速射流为喷动气的声场导向管喷流床中，大聚团被射流卷入喷射区后，外层小聚团可能会被高速射流剪切下来，使原聚团尺寸减小；进入导向管后，由于不同尺寸的聚团在气流中的运动速度存在差异，聚团间会发生碰撞，可能导致聚团黏结长大；而当聚团离开导向管落入环隙区后，声波产生的振荡气流和声湍流效应有利于聚团在气流中均匀分散，改善其在环隙的流化质量，但由于声波振荡气速远低于射流气速，很难进一步减小聚团尺寸。因此，可以认为，在声场导向管喷流床中，聚团尺寸主要取决于高速射流对聚团的剪切作用和聚团在导向管内的碰撞作用。

1.2 模型假设

（1）假设大聚团是由各种尺寸的小聚团构成，且聚团均为球形；

（2）忽略粉体与流化床之间的壁面效应，忽略Bassett力、虚拟质量力；

（3）颗粒、气体进入流化床前均充分干燥，不考虑颗粒间的液桥力和静电力，颗粒间黏附力只考虑范德华力。

1.3 受力分析

1.3.1 射流剪切作用 在喷射区，大聚团与外侧小聚团分离前以相同的速度运动，但由于大小聚团受到的外力（气流曳力和表观重力）不同，导致聚团间产生剪切力，当剪切力大于聚团间因黏附力而产生的静摩擦力时，聚团发生分裂。

图1为大小聚团在气流中沿铅锤方向的受力，图中D、d为大小聚团受到的气流曳力，G、g为大小聚团的表观重力，van为大小聚团间的黏附力。

假设作用在聚团接触点处的剪切力为0，根据牛顿第二定律，可分别列出两聚团沿铅锤方向的运动方程。

大聚团

小聚团

(2)

式中，dp/d为聚团的加速度，分离前两聚团的加速度相等。由式（1）、式（2）可得到聚团间的剪切力0

当该力能克服聚团间黏附力产生的静摩擦力，即满足式（4）时，小聚团脱离大聚团

(4)

在喷射区，高速射流可将聚团外层黏结的小聚团剪切下来，使原聚团尺寸减小；由于聚团在导向管和环隙区不断循环，聚团不断受到射流的剪切作用，最终形成有稳定粒度分布的聚团。

上述各种作用力的计算如下。

在喷射区，聚团受到的曳力为

聚团的表观重力为

(6)

聚团间的黏附力主要为范德华力，基于Israelachvili[19]的分子及表面间力的理论，两聚团间的范德华力为

式中，、分别为大小聚团的直径，H为Hamaker常数，为聚团间存在范德华力的最大距离[20]。

射流剪切作用产生的聚团粒度范围的确定如下。

（1）用MATLAB解平衡方程式（4）的结果如图2所示，图中阴影部分即为满足不等式（4）的区域，即剪切产生的聚团尺寸在此范围内。由于聚团在导向管喷动床中不断循环，会连续受到气流的剪切作用，较大聚团的尺寸会不断减小，当其值达到图中max所示值时，射流不能进一步破碎聚团，此即为剪切作用产生的最大聚团尺寸。

（2）大聚团尺寸越大，能剪切下来的小聚团尺寸越小。本实验中大聚团直径最大不会超过喷流床直径，由此确定最小聚团的尺寸min。

1.3.2 导向管内聚团间的碰撞作用 聚团随气流进入导向管后，尺寸不同的聚团由于运动速度不同可能会发生碰撞，当碰撞力大于聚团间黏附力时，聚团发生分离，反之，两聚团黏聚结合在一起（图3），即

以下为上述作用力的计算

基于Timoshenko等[13]的弹性理论，聚团间碰撞力[21]为

式中，是关于泊松比和杨氏模量的函数，一般取值3×10-10Pa-1；为相对碰撞速度，此处取为大小聚团的终端速度差，即

(10)

t为聚团的终端速度，可由式（11）求得

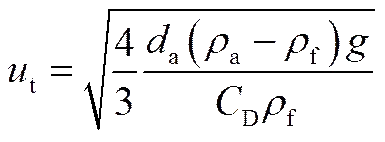
其中，曳力系数D取决于颗粒Reynolds数p的大小，由文献[22]知，当p≤1000时

(12)

聚团间黏附力van的计算与式（7）相同。

两聚团发生碰撞时，当碰撞力c大于聚团间黏附力van时，两聚团分离，相反则发生二次团聚，生成新的聚团。假设聚团密度一定，新聚团的尺寸可由质量守恒求得

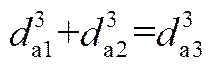
用MATLAB对上述过程进行算法设计，确定聚团粒度分布如下。

（1）在射流剪切作用产生的聚团直径范围min～max内，随机产生104个聚团。

（2）随机选取群体内两个聚团，假设两聚团同心同向碰撞，计算得到相对碰撞速度，进而比较碰撞力c和黏附力van的大小，当c较大时，输出原聚团的尺寸；反之，两聚团黏结并输出新聚团尺寸。

（3）当群体内所有聚团均被选中过（已被选择和新产生的聚团不会被再一次选中），碰撞结束，输出聚团尺寸。

1.4 参数估计

（1）两聚团间范德华力作用的最大距离一般取值4×10-10 m，聚团间的摩擦系数取值0.5[23]。

（2）Hamaker常数H可由式（14）[24]求得

式中，B为Boltzmann常数，取值1.38×10-23J·K-1；为普朗克准数，取值6.626×10-34J·s；e为UV吸附频率，取值3.0×1015s-1；指实验温度；1、1分别为物料折射率、介电常数，通过物性手册查得，TiO2的折射率1=2.616，介电常数1=40；2、2分别为流化气体的折射率、介电常数，通常取值2=2=1；计算得TiO2的Hamaker常数为4.13×10-19J。

（3）聚团密度a借助分形理论[25]进行计算

式中，p为粉体颗粒密度；f是流化聚团的分形维数，此值由拍摄所得聚团的图像根据面积-周长法[26]求得

(16)

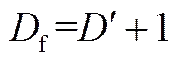
拟合聚团周长ln关于聚团面积ln的散点图，得到斜率′，进而求得分形维数，与用床层膨胀法[27]及床层沉降速度法[28]所求分形维数值较接近，将其代入式(15)得实验条件下的聚团密度。

（4）计算聚团在喷射区受到的曳力时，剪切气速为射流气速0及声波产生的振荡气速幅值rms之和，即

=0+rms(18)

rms可由式（19）[29]求得

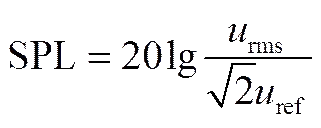
式中，ref指参考气速，通常取值4.83×10-8m·s-1。SPL=120 dB时，由式（19）求得振荡气速幅值rms=0.068 m·s-1。

（5）聚团的颗粒Reynolds数p由式（20）求得

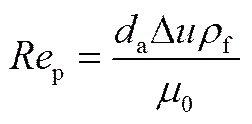
式中，Δ是指聚团与气体间的相对速度。在射流剪切区，聚团刚进入时相对速度最大，此时聚团可视为静止不动，故Δ取为射流气速；而在导向管内聚团的加速时间很短，大约在10-5s，基本以终端速度在运动，故在导向管内Δ取为聚团的终端速度t。

（6）粉体经射流剪切后，计算了选取不同聚团个数碰撞后得到的聚团平均直径及标准偏差，发现聚团个数超过5000个后，聚团的粒度分布、平均直径和标准偏差已趋于稳定，因此在模型中选取了10000个聚团进行聚团间的碰撞计算。

2 实 验

2.1 实验装置

实验装置如图4所示，主要由导向管喷流床、声波发生系统和聚团尺寸检测系统3部分组成。流化床床体由有机玻璃制成，为半圆柱形，内径120 mm，高1200 mm；喷嘴直径3 mm，导向管内径30 mm，长300 mm，导喷距50 mm；流化气体分布板为倒锥形，锥角90°，开孔率3.7%，孔径1 mm。来自压缩机的空气经过滤干燥后分为两路：一路经转子流量计后由喷嘴进入床内，为喷动气；另外一路经转子流量计后通过锥形气体分布板进入床内，为流化气。声波发生系统主要包括一台带功放的数字信号发生器和一只扬声器，由数字信号发生器获得特定频率的正弦波，通过功放放大后送入扬声器，产生声波，声波经流化床上部引入床内。聚团尺寸检测系统由POINT GREY工业相机配置NAVITAR Zoom 6000的放大镜头及PC端的粒径分析软件组成。

1—compressor; 2—dryer; 3—rotameter; 4—loudspeaker; 5—amplifier; 6—sound generator; 7—draft tube; 8—industrial camera; 9—PC

2.2 实验物料

实验物料为上海江沪钛白化工制品生产的金红石型纳米级TiO2，其物理性质如表1所示。原生颗粒粒径由湖南润之科技的纳米激光粒度仪Rise-2002测定，粒度分布如图5所示，平均粒径为290 nm。图6是由OXFORD instruments公司的场发射扫描电子显微镜拍得的扫描电镜图。实验前先把粉体置于烘箱中，在120℃下烘焙3 h后，放入干燥皿中冷却至室温备用。

表1 物料性质

2.3 实验方法

实验测定了频率80 Hz、声强120 dB的声波作用下，流化气速0.2 m·s-1时[12]，TiO2超细粉在不同射流气速下形成的聚团尺寸。聚团尺寸采用显微摄像结合图像分析获得。因流化时粉体易黏附在床壁，使得从外部很难拍到流化床内清晰的聚团图像，且壁面也会影响拍得聚团图像的真实性；而取出采样又不可避免会造成聚团的破碎，影响测试结果，所以本文采用喷出采样法进行测量，即在导向管的中心线处，分别在床层上部、中部及下部开一个2 mm的孔，并用胶带密封，待物料在流化床中达到稳定循环，将胶带打开，此时物料会喷出流化床，用聚团尺寸检测系统进行采样。为使得到的聚团尺寸具有代表性，每个实验条件下测3组数据（即从流化床上部、中部及下部采样），每组分析约1000个聚团。

图7为射流气速为60 m·s-1时拍得的聚团图像，图中白点表示聚团。用粒度分析软件对图像进行分析，所得聚团尺寸分布如图8所示。

表2 模型计算与实验测量尺寸分布的比较

Note: Cal.—calculated value; Exp.—experimental value; Dev.—deviation ratio.

3 结果分析

图9为不同射流气速下，聚团平均直径的模型计算值与实测值的比较。由图可知，随着射流气速的增大，由于剪切作用和碰撞作用增强，聚团平均直径减小，模型预测值与实测值的趋势一致，且偏差均小于15%，因此，该模型可很好地预测TiO2在声场导向管喷流床中流化时的聚团平均直径。另由图可知，模型计算值略小于实验测量值，这可能是由于实验条件下，聚团难以到达射流核心区，使聚团实际受到的剪切作用小于理论值所致。表2为不同射流气速下，表征聚团尺寸分布的特征参数（中位径50、最频径m及标准偏差）的模型计算值与实验值的比较，从表中数据可知，中位径50和最频径m模型预测值的偏差小于15%，标准偏差模型预测值的偏差小于25%，说明模型可较好地预测该实验条件下聚团尺寸的分布情况。综上所述，该聚团尺寸预测模型可较好地预测声场导向管喷流床中超细粉聚团的平均直径及尺寸分布。

4 结 论

通过对声场导向管喷流床中超细粉聚团形成过程的分析，提出高速射流的剪切作用和聚团间的碰撞作用是决定聚团尺寸的主要原因。在此基础上，结合聚团在射流剪切过程和碰撞过程的受力分析，建立了预测声场导向管喷动流化床中超细粉聚团尺寸分布的力平衡模型，并据此模型计算了平均粒径为290 nm的TiO2超细颗粒在不同射流气速下聚团的平均粒径、粒度分布和标准偏差，模型预测值与实验结果吻合较好。

符 号 说 明

A——聚团投影面积，m3 AH——Hamaker常数 CD——曳力系数 D——大聚团直径，m Df——分形维数 d——小聚团直径，m dm——最频径，m d50——中位径，m Fc——碰撞力，N FD——大聚团受到的曳力，N Fd——小聚团受到的曳力，N FG——大聚团的表观重力，N Fg——小聚团的表观重力，N Fvan——范德华力，N F0——聚团间相互作用力，N h——普朗克准数，J·s M——大聚团质量，kg m——小聚团质量，kg P——聚团投影周长，m Rep——颗粒Reynolds数 T——温度，K u——剪切气速，m·s-1 Δu——相对速度，m·s-1 uref——参考气速，m·s-1 urms——振荡气速，m·s-1 ut——终端气速，m·s-1 u0——射流气速，m·s-1 V——碰撞速度，m·s-1 δ——颗粒间距离，m ε——介电常数 µ——摩擦因子 µ0——气体黏度，Pa·s ρa——聚团密度，kg·m-3 ρf——气体密度，kg·m-3 ρp——颗粒密度，kg·m-3 σ——标准偏差

References

[1] 王垚, 金涌, 魏飞, 等. 原生纳米级颗粒的聚团散式流态化[J]. 化工学报, 2002, 53(4): 344-348. WANG Y, JIN Y, WEI F,. Agglomerate particulate fluidization of primary nano-particles[J]. Journal of Chemical Industry and Engineering(China), 2002, 53(4): 344-348.

[2] HONG R, DING J, LI H. Fluidization of fine powders in fluidized beds with an upward or a downward air jet[J]. China Particuology, 2005, 3(3): 181-186.

[3] 张国杰, 皮立强, 杨兴灿, 等. 超细粉在内循环流化床中的流态化特性[J]. 化学反应工程与工艺, 2015, 31(3): 262-265.ZHANG G J, PI L Q, YANG X C,. Fluidization behavior of ultrafine powders in an internal circulating fluidized-bed[J]. Chemical Reaction Engineering and Technology, 2015, 31(3): 262-265.

[4] 张国杰. 超细粉在内循环流化床中的流态化[D]. 成都: 四川大学, 2013. ZHANG G J.Fluidization behavior of ultrafine powders in an internal circulating fluidized bed[D]. Chengdu: Sichuan University, 2013.

[5] ZHU X, ZHANG Q, WANG Y,. Review on the nanoparticle fluidization science and technology[J]. Chinese Journal of Chemical Engineering, 2016, 24(1): 9-22.

[6] LIANG X, DUAN H, ZHOU T,Fluidization behavior of binary mixtures of nanoparticles in vibro-fluidized bed[J]. Advanced Powder Technology, 2014, 25(1): 236-243.

[7] SI C D, ZHOU J, GUO Q J,The effect of acoustic field on the particle concentration profiles in fluidized bed[J]. International Journal of Chemical Reactor Engineering, 2012, 12: 1-13.

[8] QUEVEDO J A, OMOSEBI A, PFEFFER R. Fluidization enhancement of agglomerates of metal oxide nanopowders by microjets[J]. AIChE Journal, 2010, 56(6): 1456-1468.

[9] DUAN H, LIANG X, ZHOU T,. Fluidization of mixed SiO2and ZnO nanoparticles by adding coarse particles[J]. Powder Technology, 2014, 267: 315-321.

[10] ZHU X, ZHANG Q, WANG Y,. Review on the nanoparticle fluidization science and technology [J]. Chinese Journal of Chemical Engineering, 2016, 24(1): 9-22.

[11] 周勇, 马兰, 石炎福. 超细粉在导向管喷动床中的固体循环速率[J]. 化工学报, 2004, 55(9): 1532-1536. ZHOU Y, MA L, SHI Y F. Solids circulation of ultra-fine powders in spouted bed with draft tube[J]. Journal of Chemical Industry and Engineering(China), 2004, 55(9): 1532-1536.

[12] 皮立强, 高凯歌, 杨兴灿, 等. 纳米 TiO2颗粒在声场导向管喷动流化床中的流化特性[J]. 化学反应工程与工艺, 2016, 32(2): 114-119. PI L Q, GAO K G, YANG X C,. Fluidization characteristics of TiO2nanoparticles in an acoustic spouted-fluidized bed with a draft tube[J]. Chemical Reaction Engineering and Technology, 2016, 32(2): 114-119.

[13] TIMOSHENKO S, GOODIER J. Theory of Elasticity [M]. New York: McGraw-Hill Book, 1970: 102.

[14] MARTIN L D, OMMEN R V. A model to estimate the size of nanoparticle agglomerates in gas-solid fluidized beds[J]. Journal of Nanoparticle Research, 2013, 15(11): 2055.

[15] MARTIN L D, OMMEN R V. Estimating the size of polar and apolar nanoparticle agglomerates in a fluidized bed[J]. Journal of Politics, 2013, 56(56): 818-823.

[16] LIANG X, WANG J, ZHOU T,. Modified model for estimation of agglomerate sizes of binary mixed nanoparticles in a vibro-fluidized bed[J]. Korean Journal of Chemical Engineering, 2015, 32(8): 1515-1521.

[17] LIANG X, ZHOU Y, ZOU L,. Fluidization behavior of binary iron-containing nanoparticle mixtures in a vibro-fluidized bed[J]. Powder Technology, 2016, 304: 101-107.

[18] ZHOU L, WANG H, ZHOU T,. Model of estimating nano-particle agglomerate sizes in a vibro-fluidized bed[J]. Advanced Powder Technology, 2013, 24(1): 311-316.

[19] ISRAELACHVILI J N. Intermolecular and Surface Forces: with Applications to Colloidal and Biological Systems[M]. New York: Academic Press, 1985: 77.

[20] MOROOKA S, KUSAKABE K, KOBATA A,. Fluidization state of ultrafine powders[J]. Journal of Chemical Engineering of Japan, 1988, 21(1): 41-46.

[21] ZHOU T, LI H. Force balance modelling for agglomerating fluidization of cohesive particles[J]. Powder Technology, 2000, 111(1): 60-65.

[22] 袁竹林, 朱立平, 耿凡. 气固两相流动与数值模拟[M]. 南京: 东南大学出版社, 2013:35. YUAN Z L, ZHU L P, GENG F. Gas-Solid Two Phase Flow and Numerical Simulation[M]. Nanjing: Southeast University Press, 2013: 35.

[23] CHIRONE R, MASSIMILLA L, RUSSO S. Bubble-free fluidization of a cohesive powder in an acoustic field[J]. Chemical Engineering Science, 1993, 48(1): 41-52.

[24] BUTT H J, KAPPL M. Surface and Interfacial Forces[M]. New York: John Wiley & Sons Inc., 2009: 34.

[25] MARTIN L D, FABRE A, RUUD VAN OMMEN J. The fractal scaling of fluidized nanoparticle agglomerates[J]. Chemical Engineering Science, 2014, 112: 79-86.

[26] SÁNCHEZ-LÓPEZ J C, Fernández A. TEM study of fractal scaling in nanoparticle agglomerates obtained by gas-phase condensation[J]. Acta Materialia, 2000, 48(14): 3761-3771.

[27] NAM C H, PFEFFER R, DAVE R N,. Aerated vibrofluidization of silica nanoparticles[J]. AIChE Journal, 2004, 50(8): 1776-1785.

[28] QUINTANILLA M, VALVERDE J, ESPIN M,. Electrofluidization of silica nanoparticle agglomerates[J]. Industrial & Engineering Chemistry Research, 2011, 51(1): 531-538.

[29] RUSSO P, CHIRONE R, MASSIMILLA L,. The influence of the frequency of acoustic-waves on sound-assisted fluidization of beds of fine particles[J]. Powder Technology, 1995, 82(3): 219-230.

Prediction of agglomerate size for ultrafine particles in acoustic spouted fluidized-bed with draft tube

GAO Kaige, LEI Yuzhuang, LI Hainian, ZHOU Yong

(School ofChemical Engineering, Sichuan University, Chengdu 610065, Sichuan, China)

The fluidization property of ultrafine particles is closely related to their agglomerate size. Through the analysis of the formation process of ultrafine powder agglomerates in an acoustic spouted fluidized-bed with a draft tube, it is proposed that the shearing action of high speed jet and collision between agglomerates were the dominating factors to influence agglomerate size. Based on the force balance analysis acting on the agglomerates during the jet shearing process and collision between agglomerates, a model to predict agglomerate size distribution in an acoustic spouted fluidized-bed with a draft tube was established. The average size of agglomerates and their size distribution of TiO2ultrafine powder at different jet velocities in the bed were predicted by the model successfully.

nanoparticles; acoustic spouted fluidized-bed with draft tube; shearing action of high speed jet; collision between agglomerates; particle size distribution; prediction model

10.11949/j.issn.0438-1157.20161792

TQ 021

A

0438—1157（2017）06—2290—08

周勇。

高凯歌（1992—），女，硕士。

国家自然科学基金项目（21376151）。

2016-12-23收到初稿，2017-02-28收到修改稿。

2016-12-23.

ZHOU Yong, zhouyong@scu.edu.cn

supported by the National Natural Science Foundation of China(21376151).