判定平行四边形的几种猜想

鲁仁伟

判定平行四边形的几种猜想

鲁仁伟

同学们都已学习过“三角形全等的判定条件”了，试试将这部分知识迁移到平行四边形中.已知四边形ABCD，下面有7个猜想：

（1）两组对角相等；

（2）一组对边相等且另一组对边平行；

（3）一组对边相等且一组对角相等；

（4）一组对边平行且一组对角相等；

（5）一组对边相等且一条对角线被另一条对角线平分；

（6）一组对边平行且一条对角线被另一条对角线平分；

（7）一组对角相等且一条对角线被另一条对角线平分.

这7个猜想能判定四边形ABCD是平行四边形吗？接下来，我们将一一论证.

猜想1：两组对角相等的四边形是平行四边形

已知四边形ABCD，如图1，∠A=∠C，∠B=∠D.求证：四边形ABCD是平行四边形.

图1

证明：∵∠A+∠B+∠C+∠D=360°，∠A=∠C，∠B=∠D，

∴2∠A+2∠B=360°，∴∠A+∠B=180°，

∴AD//BC，同理，AB//CD.

∴四边形ABCD是平行四边形.

因此，猜想1正确.

猜想2：一组对边相等且另一组对边平行的四边形是平行四边形

满足猜想2的四边形可以是等腰梯形，所以猜想2是不成立的.

猜想3：一组对边相等且一组对角相等的四边形是平行四边形

图2

如图2，以平行四边形ABCD的边BC为半径，以点B为圆心画圆，再作△BCD的外接圆，与⊙B交于点C和点C′，连接C′B、C′D，

∵BC′=BC，∴AD=BC′，

∵∠C=∠C′，∴∠A=∠C′，

∴四边形ABC′D有一组对边相等和一组对角相等，但不是平行四边形，所以猜想3不正确.

猜想4：一组对边平行且一组对角相等的四边形是平行四边形

已知四边形ABCD，如图3，AB//CD，∠B=∠D.求证：四边形ABCD是平行四边形.

图3

证明：∵AB//CD，∴∠A+∠D=180°，

∵∠B=∠D，∴∠A+∠B=180°，∴AD//BC.

∴四边形ABCD是平行四边形.所以猜想4正确.

猜想5：一组对边相等且一条对角线被另一条对角线平分的四边形是平行四边形

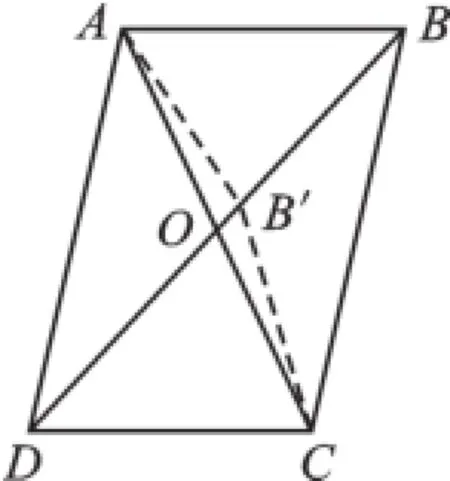
图4

如图4，以平行四边形ABCD的边AB为半径，以点A为圆心画弧，交对角线BD于点B′，连接AB′和B′C，则四边形AB′CD符合猜想5的条件，但不是平行四边形，所以猜想5不正确.

猜想6：一组对边平行且一条对角线被另一条对角线平分的四边形是平行四边形

已知四边形ABCD，如图5，对角线AC和BD相交于点O，且AB//CD，AO=OC.求证：四边形ABCD是平行四边形.

图5

证明：∵AB//CD，

∴∠ABD=∠BDC，∠BAC=∠DCA，

在△AOB与△COD中，OA=CO，∠ABD=∠BDC，∠BAC=∠DCA，

∴△AOB≌△COD.∴OB=OD.

∵OA=OC，

∴四边形ABCD是平行四边形，猜想6正确.

猜想7：一组对角相等且一条对角线被另一条对角线平分的四边形是平行四边形

图6

如图6所示，已知线段AC垂直平分BD，垂足为O，显然OB=OD.依据垂直平分线上的点到线段两端的距离相等，连接A、B、C、D，易得AB=AD，CB=CD.依据等腰三角形的性质，易得∠ABD=∠ADB，∠CBD=∠CDB，所以∠ABC=∠ADC.四边形ABCD满足猜想7的条件，但不是平行四边形，所以猜想7不正确.

同学们，学习数学不能局限于教材.类比全等三角形的判定方法，探究平行四边形的判定方法，你有什么收获吗？

江苏省扬州市田家炳实验中学）