例谈一类双变量不等式的证明

■陕西省西安市临潼区马额中学 童永奇

例谈一类双变量不等式的证明

■陕西省西安市临潼区马额中学 童永奇

双变量问题难度大,试题新颖,很多同学无从下手,下面通过举例剖析的形式,着重说明两个问题:一是证明与函数紧密相关的双变量不等式问题的常用方法;二是帮助同学们理清内在规律,便于迅速求解同类问题。

例题：已知函数f(x)=l nx-ax(a∈R)有两个不同的零点x1,x2,求证:x1x2＞e2。

分析：本题看似简单,但实际较难,具有一定的综合性,涉及函数、导数、不等式等知识。从题设出发,需要进一步明确已知条件,借助数形结合、适当变形,发现特点;从待证式出发,可活用分析法等价转化目标问题,以便构造函数,借助导数加以证明。

又f(1)=-a＜0,不失一般性,若设x1＜x2,则由f(x)的图像知

因为x1,x2是函数f(x)=l nx-ax的零点,所以f(x1)=l nx1-ax1=0,f(x2)= l nx2-ax2=0。

故l nx1=ax1,① l nx2=ax2。②

由①+②得,l n(x1x2)=a(x1+x2)。③

由①-②得,l nx1-l nx2=a(x1-x2)。④

接下来,可采取几种不同的思维方法加以灵活证明,请赏析。

方法一：因为由③知,要证x1x2＞e2,即证a(x1+x2)＞2,即证设函数则因为0,所以函数g(t)在(0,1)上单调递增,所以g(t)＜g(1)=0,即 ,故得证。

方法二：由③÷④得:

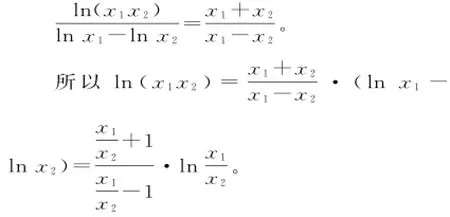
于是,要证x1x2＞e2,即证2,即证以下同方法一,略。

方法三：由方法一知,要证x1x2＞e2,即证

又易知f(x1)=f(x2),所以即证f(x1)

评注:上述各方法的共同特点是均需要构造新函数,并利用新函数的单调性加以证明,但具体探寻新函数的途径不尽相同——其中方法一、方法二的关键在于经过适当的变形、换元,并借助分析法,等价转化为证明关于“t”的不等式问题;方法三的关键在于借助分析法,结合函数f(x)的性质,等价转化为证明关于“x1”的不等式问题。此外,对比方法一、方法二可知,方法二的变形较为简单,值得我们去回味、深思。

练一练：

1.已知函数f(x)=l nx-ax2(a∈R)。

(2)在(1)的条件下,若f(m)=f(n),且m＜n,求证:m+n＞4a。

2.已知函数f(x)=ax2-ex(a∈R)在(0,+∞)上的两个零点分别为x1,x2,并且x1＜x2。

(1)求实数a的取值范围;

(2)求证:x1+x2＞4。

(1)求实数m的取值范围;

(责任编辑 徐利杰)