基于EMD与小波分析的设备故障诊断研究与分析∗

基于EMD与小波分析的设备故障诊断研究与分析∗

印嘉

（阿坝师范学院物理与电子科学系汶川623002）

论文提出了一种基于EMD与小波分析相结合的设备故障故障诊断方法，先采用EMD变换对原始振动信号进行分解，再对去分解后得到的IMF进行小波分析处理，并选择其中最具代表性的部分IMF进行HHT边际谱分析，实现了对设备故障有效的诊断和研究。实验表明，通过基于EMD与小波分析相结合的方法对设备故障诊断是有效的和可行的。

EMD；小波分析；边际谱；故障诊断

Class NumberTP277

1 引言

机械设备运行中，设备产生的振动信号蕴含了非常丰富状态信息。在机械设备发生故障的早期，其特征信号极为微弱，容易被强噪声淹没，这样就在一定程度上影响了设备的特征信号的有效获取［1］。因此，以机械设备为研究对象的故障诊断技术，越来越收到关注，成为了当前的一个研究热点。

设备的失效是致命的，一旦出现故障，将造成巨大的经济损失，甚至人员伤亡。因此，对设备故障诊断研究有着重要的价值和意义［2］。本文提出了一种基于EMD与小波分析相结合的故障诊断方法，先采用经验模式分解方法EMD变换对原始振动信号进行分解，得到有限多个本征模态函数IMF，然后对去分解后得到的IMF进行小波分析，并选择其中最具代表性的部分IMF进行HHT边际谱分析，最后可以得到对应的HHT边际谱分析，通过分析具有强烈故障特征的IMF边际谱的变化特征，从而确定设备故障特征，实现故障诊断的研究与分析。

2 EMD与HHT原理

由于HHT的完备性和自适应，它适用于分析非平稳信号［3］。复杂信号可以由EMD方法分解为有限多个本征模态函数IMF（Intrinsic Mode Func⁃tion），再利用Hilbert变换，求解各IMF的瞬时频率和瞬时幅值，从而获得信号的Hilbert谱和边际谱，进而实现对故障的诊断分析［4］。

2.1EMD方法

EMD方法是从复杂信号里分离IMF的过程，基于任何复杂的信号都是从一些不同的IMF组成的假设，对复杂信号进行“筛选”（sifting process），从而使得复杂信号经Hilbert变换后的瞬时频率具有了物理意义。EMD分解过程简述如下：

1）确定信号想x(t)所有的局部极值点；

2）用三次样条线分别将所有的局部极大和极小点连接起来形成上、下包络线；

3）上下包络线的平均值记为m(t)，求出：

核对，如果c(t)是一个IMF，则c(t)就是x(t)第一个IMF分量，把c(t)从x(t)中分离出来得到残余函数：

否则把c(t)作为原始数据，重复步骤1）～3）。

4）重复步骤1）～3），直到r(t)成为一个单调函数不能再从中提取满足IMF条件的分量时，循环结束。完成EMD的分解过程。

这样，原信号可表示为一个残余函数与n个IMF函数之和：

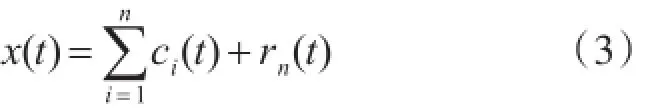
2.2HHT与边际谱

在分解得到本征模态函数IMF之后，对其进行Hilbert变换，计算得到瞬时频率［5］。首先，对所有IMF做Hilbert变换，即：

构造解析信号，得到幅值和相位函数：

求出瞬时频率为

则

这里省略了残余量rn(t)，Re表示取实部，H(w,t)称成为Hilbert谱。进一步定义边际谱：

式中，T为信号的总长度。得到瞬时频率和幅值即可描述为原信号的时频，Hilbert谱精确地描述了信号的幅值在整个频率段上随时间和频率的变化规律，而h(w)反映了信号的幅值在整个频率段上随频率的变化情况［6～7］。

3 小波分析

小波分析是通过使用窗函数，使形状可以发生改变，但时频窗面积不变。小波函数根据需要调整时间与频率分辨率，具有多分辨率分析的特点［8］。

在小波分析中，主要讨论的函数空间为L2(R)。L2(R)指R上平方可积函数构成的函数空间，即：

若f(t)∈L2(R)，则称f(t)为能量有限的信号。L2(R)也常称为能量有限的信号空间。

如果ψ(t)∈L2(R)，其傅里叶变换为ψ(w)满足容许性条件（Admissible Condition）：

即Cψ有界，则称ψ为一个基小波。将基小波经过伸缩和平移后可以得到一个小波序列：

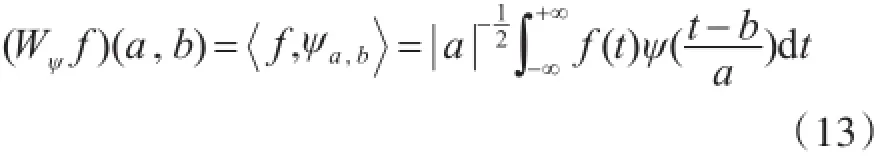
式（3）中，a,b∈R，且a≠0。称a为伸缩因子，b为平移因子。定义下式：为关于基小波ψ的连续小波变换。显然，变换后的函数是二维的，即小波分析把原来的一维信号变换成二维信号，以便分析函数的时频特性。

小波分析的本质在于将L2(R)空间中的任意函数f(t)表示成其在具有不同伸缩因子a和平移因子b的ψa,b(t)之上的投影的叠加。与傅里叶变换不同的是，小波分析将一维时域函数映射到二维“时间-尺度”域上［9～10］。因此f(t)在小波基上的展开具有多分辨率的特性。通过调整伸缩因子a和平移因子b，可以得到具有不同时频宽度的小波以匹配原始信号的任意位置，达到对信号的时频局部化分析的目的。

4 实验仿真验证

本文采用美国Case Western Reserve University发布的振动信号数据为实验仿真数据，进行仿真实验和验证方法的可行性与有效性。图1为原始异常振动信号，图2为原始正常振动信号。通过查看图1和图2的频率特征，可以得到振动幅值发生了明显的变化，说明设备出现了异常状况，但是无法确定具体故障特征。因此需要对信号数据进行更加深入的分析与研究。

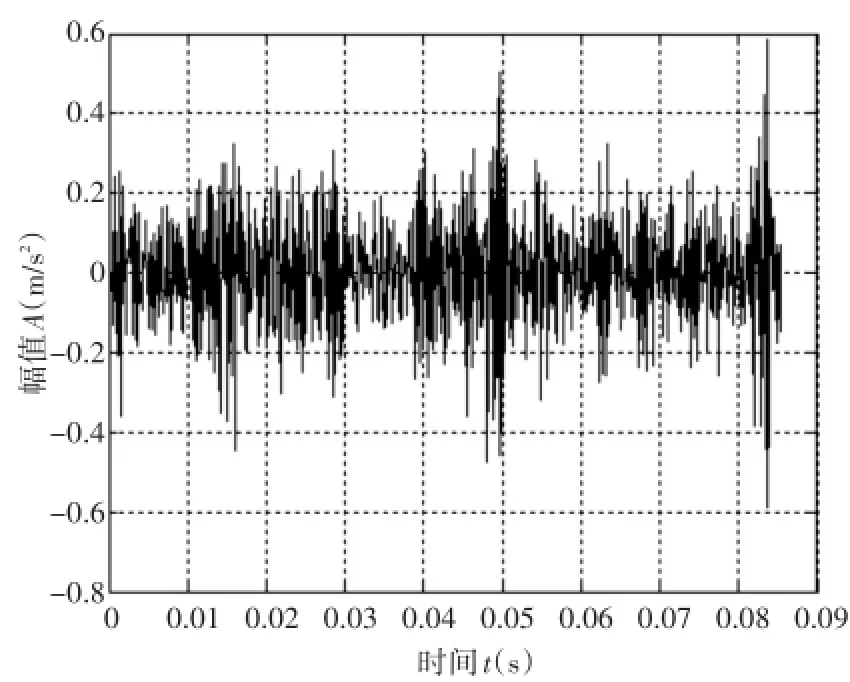
图1 原始异常振动信号

图2 原始正常振动信号

为了进一步地实施对振动信号进行分析与研究，可以通过对原始信号进行EMD分解处理，得到振动信号对应的时频谱，分解过程如图3。图3是EMD分解异常振动信号的IMF。从图3中可以看出，EMD分解是将振动信号从高频到低频逐一分解的过程，异常振动信号被分解为七个IMF和一个残余量Res，每个IMF的频率依次从上到下呈逐渐降低。这里的每个IMF均包含了此频段所独有的频率特征，也就是故障振动信号的特征频率，对故障诊断的研究提供不错的依据。这里可以将这个残余量Res舍去。

接着，可以对每个IMF再进行小波分析，去除信号里面的噪声和杂质，保留信号的有效成分。图4是小波分析后的异常振动信号的IMF，图5是小波分析后的正常振动信号的IMF。

图3 EMD分解异常振动信号的IMF

图4 小波分析后的异常振动信号的IMF

图5 小波分析后的正常振动信号的IMF

通过研究图4和图5，可以发现小波分析在异常振动信号的处理上起到了有效的作用。原IMF在经过小波分析处理后，噪声信息得到了合理的去除，只保留了有效的信息。显然，IMF1由复杂的信号幅值变为主要集中在［0.01，0.02］，［0.05，0.05］和［0.08，0.09］三个时间段。IMF2的信号幅值主要集中在［0.01，0.03］，［0.04，0.06］和［0.08，0.09］三个时间段。可见几乎每个IMF的振幅特征都发生了或多或少的变化。在设备的故障诊断研究过程中，可以通过有针对性地分析和研究部分IMF的特点，来对设备的运行状况进行分析，实现故障诊断的目的。

而且，可以发现IMF1～IMF4在小波分析之后，信号特征的变化较为明显，其蕴含的振动信息量比较丰富。因此，本文以IMF1～IMF4作为主要的研究对象，分析其特征，来实现对设备故障诊断的研究与分析。

利用Hilbert变换在对其中最有代表性的IMF1-IMF4进行处理，可以得到IMF的瞬时频率和瞬时幅值，从而获得信号的Hilbert边际谱，进而实现对故障的诊断。图6为原始信号的边际谱，图7为去噪后的信号的边际谱。

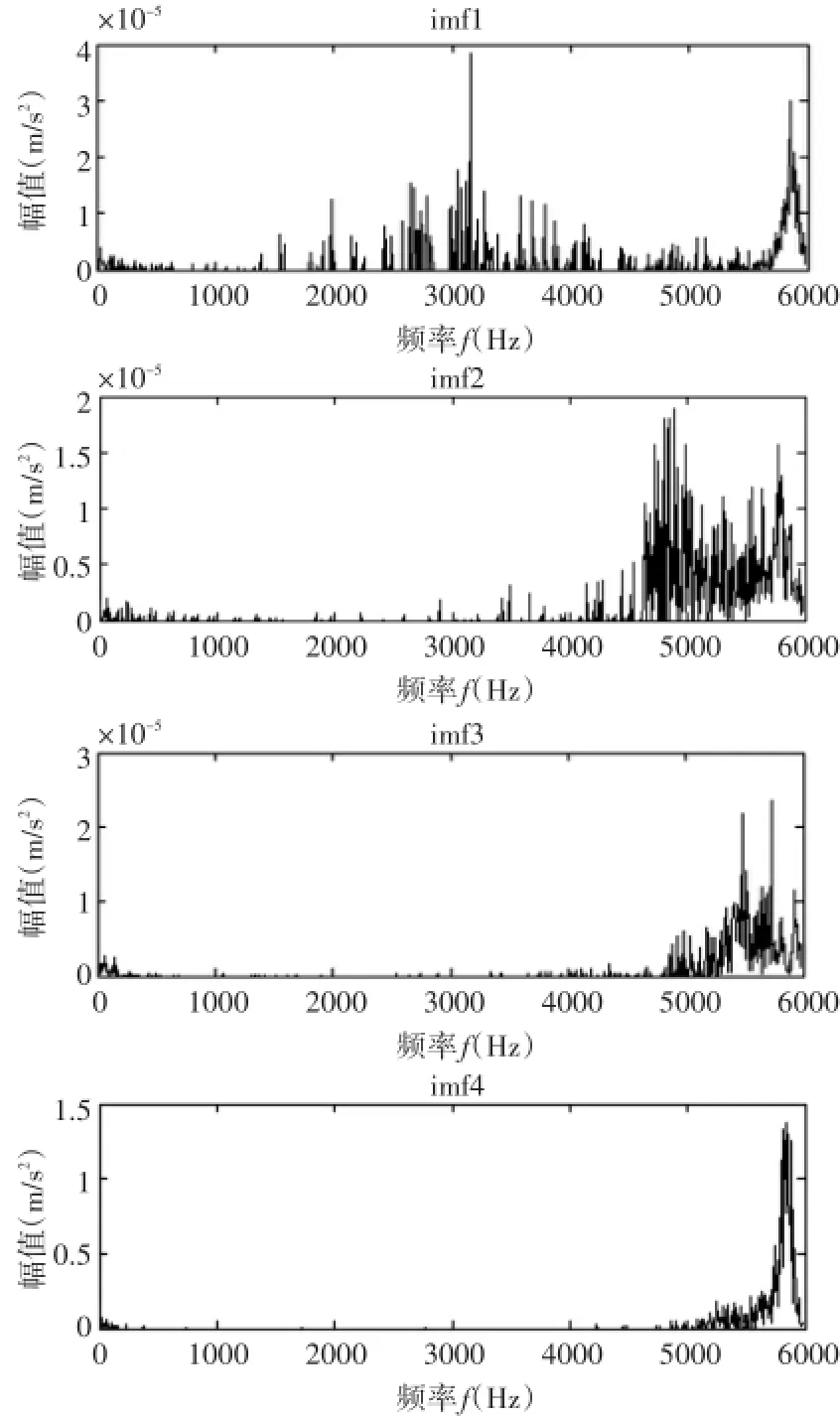
图6 异常振动信号IMF1～IMF4的边际谱

图7 正常振动信号IMF1～IMF4的边际谱

通过对比和分析图6和图7，可以清晰的得出，正常振动信号的IMF1的振动频率主要集中在4500Hz～6000Hz，而异常振动信号的IMF1的在2000Hz～4000Hz出现了大量的异常振动信号，且在3000Hz处出现了一个波峰。正常振动信号的IMF2的振动频率主要集中在4000Hz～6000Hz，而异常振动信号的IMF2的在4500Hz～5500Hz出现了大量的异常振动信号，且幅值有了明显的增大。正常振动信号的IMF3的振动频率主要集中在5500Hz～6000Hz，而异常振动信号的IMF3的在5000Hz附件出现了大量的异常振动信号，且幅值也有了明显的增大。IMF4的正常振动信号和异常振动信号的主要频率都是集中在4500Hz～6000Hz，只是在振幅上有所增大。可见，设备的边际谱发生了明显的变化，也就是设备出现了问题，需要设备管理维护人员有针对性对故障特征进行诊断和研究分析。

通过对比和研究IMF的边际谱的变化情况，可以找到设备的特征频率的变化情况，对了设备工作的定位和确诊提高了有力的证据，就避免了在故障诊断的过程中盲目的进行分析，只需要有针对性的研究特定IMF的频率变化变化情况，提高了故障诊断的工作效率。

5 结语

仿真实验结果表明，在设备故障诊断中，基于EMD与小波分析的方法是有效的和可行的。通过分析去噪后得到的边际谱，能够准确地得出机械设备的运行状况。因此，基于EMD与小波分析的方法对设备故障诊断是具有广泛的应用前景。

［1］江超.大型隔膜泵组故障诊断系统研究［D］.沈阳：东北大学，2008.

JIANG Chao.Study on Failure Diagnosis System of the Large-scale Diaphragm Pump Group［D］.Shengyang：Northeastern University，2008.

［2］印嘉，吴建德，王晓东，等.基于HHT的往复式隔膜泵主轴故障诊断研究［J］.传感器与微系统，2013，32（4）：5-8.

YIN Jia，WU Jiande，WANG Xiaodong，et al.The Recipro⁃ cating Diaphragm Pump Spindle Fault Diagnosis Based on HHT［J］.Transducer and Microsystem Technology，2013，32（4）：5-8.

［3］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlin⁃ear and non-stationary time series analysis［C］//Proceed⁃ings of the Royal Society of London A.London：The Royal Society，1998，454：903-995.

［4］Espinosa A.G.，Rosero J.A.，CUSIDO J，et al.Fault Detec⁃tion by Means of Hilbert-Huang Transform of the Stator Current in a PMSM with Demagnetization［J］.Energy Con⁃version，2010，25（2）：312-318.

［5］YIN Jia，LI Qingmao，YUAN Xuyi.The Diaphragm Pump Spindle Fault Diagnosis using HHT Based on EMD［J］. The Open Automation and Control Systems Journal，2015，7：640-645.

［6］韩清凯，于晓光.基于振动分析的现代机械故障诊断原理及应用［M］.北京：科学出版社，2010：81-82.

HAN Qingkai，YU Xiaoguang.Principle and Application of Modern Mechanical Fault Diagnosis Based on Vibration Analysis［M］.Beijing：Science Press，2010：81-82.

［7］汪学渊，潘宏侠.基于EMD的电机轴承故障识别研究［J］.煤矿机械，2009：30（2）：215-217.

WANG Xueyuan，PAN Hongxia.Study on Fault Diagnosis of Motor Bearings Based on EMD［J］.Coal Mine Machin⁃ery，2009，30（2）：215-217.

［8］张晓楠，曾庆山，万红.基于改进小波去噪和EMD方法的轴承故障诊断［J］.测控技术，2014，33（1）：23-30.

ZHANG Xiaonan，CENG Qingshan，WANG Hong.Bearing Fault Diagnosis Based on Improved Wavelet Denoising and EMD Method［J］.Measurement and Control Technolo⁃gy，2014，33（1）：23-30.

［9］武建军，邓松圣，周爱华，等.自适应小波降噪的泵机组故障诊断［J］.化工自动化及仪表，2010，37（4）：36-38.

WU Jianjun，DENG Songsheng，ZHOU Aihua，et al.Pump Fault Diagnosis Based on Self-adaptive Wavelet Denoise［J］.Control and Instruments in Chemical Industry，2010，37（4）：36-38.

［10］何正嘉.机械故障诊断理论及应用［M］.北京：高等教育出版社，2010：74-81.

HE Zhengjia.Mechanical Fault Diagnosis Theory and Application［M］.Beijing：Higher Education Press，2010：74-81.

Equipment Fault Diagnosis Based on EMD and Wavelet Analysis

YIN Jia
（Department of Physical and Electronic Science，Aba Teachers University，Wenchuan623002）

This paper presents a method of equipment fault diagnosis based on the combination of EMD and wavelet analysis. Firstly it processes the signal vibration data by EMD to get some IMF，and trying wavelet analysis for each IMF，then the most repre⁃sentative parts of the IMF are chosen through Hilbert transform，finally fault diagnosis is realized and researched by the HHT mar⁃ginal spectrum of IMF，so it can realize effective diagnosis and research for equipment failure.The experimental results show that the method based on EMD and wavelet analysis for equipment fault diagnosis is effective and feasible.

EMD，wavelet analysis，marginal spectrum，failure diagnosis

TP277

10.3969/j.issn.1672-9722.2017.05.007

2016年11月12日，

2016年12月27日

四川省科技厅计划项目（编号：2011JYZ031）；四川省教育厅科研项目（编号：14ZB0339）；阿坝师院校级科研基金项目（编号：ASB16-09）资助。

印嘉，男，硕士，助教，研究方向：设备故障诊断。