基于准零刚度技术的微重力模拟悬吊装置设计与试验研究
唐 锐,黄 海,黄 舟
基于准零刚度技术的微重力模拟悬吊装置设计与试验研究
唐 锐1,黄 海1,黄 舟2
(1. 北京航空航天大学宇航学院,北京100191;2. 中国工程物理研究院总体工程研究所,绵阳 621999)
微重力地面模拟试验对验证航天器在轨运行的可靠性有重要意义。通常采用低刚度悬吊装置模拟微重力环境,但存在着承载能力低和自振干扰的问题。为解决这些问题,文章提出了一种考虑弹簧自振的准零刚度悬吊装置。首先,通过合理简化推导了承载弹簧在装置中的自振频率计算式,并分析了准零刚度悬吊装置的工作原理,得出设计参数应满足的条件。然后,根据试验承载需求和位移要求提出了参数设计流程,依此流程设计得到了一种可调节平衡位置与几何参数的准零刚度悬吊装置。最后,对装置进行了静力测试与悬吊-隔振试验,结果表明,该装置不仅具有准零刚度特性和较大承载能力,而且解决了自振干扰的问题,能较好地模拟微重力环境。
微重力模拟;准零刚度;悬吊装置;自振干扰;结构设计
0 引言
为保证航天器在轨运行的可靠性,微重力地面模拟试验是一项必不可少的工作。在已发展的多种微重力模拟技术中,悬吊法原理简单,使用灵活且可靠,成本低,应用广泛[1]。为了减小对载荷的影响,尽可能地模拟载荷处于失重时的自由状态,悬吊装置应满足质量小、刚度低的要求[2]。常用的低刚度柔性元件有弹簧、橡皮绳等,但采用这些柔性元件设计的悬吊装置承载能力低,悬吊载荷时会产生巨大变形。为了克服这些缺陷,研究人员提出利用准零刚度技术[3]来改进悬吊装置。
准零刚度技术的主要思想是并联正、负刚度元件,以获得刚度低、承载能力大的特性。该技术常被用于振动领域的低频隔振,取得了大量研究成果,如屈曲弹性钢板并联橡胶的准零刚度装置[4]、利用蝶形弹簧提供负刚度的准零刚度隔振器[5]、基于可调式空气弹簧的准零刚度隔振装置[6]以及利用磁力弹簧的准零刚度低频隔振器[7-8]等。这些装置在稳定性、可调性、结构小型化等方面各有所长,均成功用于低频隔振。NASA在较早时期做了大量关于准零刚度技术应用于微重力模拟的研究,研制了准零刚度微重力模拟悬吊装置[9];在空间结构主、被动控制研究中,利用弹簧与压杆并联形式研制的一种准零刚度悬吊装置,获得了承载90kg且变形不到2.5cm的能力和71N/m的低刚度,成功用于较大空间结构的微重力模拟[10]。Harvey提出了另一种斜拉弹簧式的准零刚度悬吊装置[11],利用侧边受拉弹簧在竖直方向上的分力可以抵消悬吊弹簧拉力的原理,实现了低刚度、小变形的能力;Crawley给出了具体的设计步骤,并且在NASA的DSMT项目中采用这种悬吊装置实现了刚度低于53N/m、悬吊载荷时的固有频率不高于0.2Hz的目标[12]。Woodard与Cooley等人对上述2种典型的准零刚度悬吊装置进行了对比研究,指出斜拉弹簧式的装置摩擦力小,适用于小位移情况;而弹簧与压杆并联的装置容易获得更大的位移范围,且参数少、易实现[13]。然而,以上关于准零刚度悬吊装置的研究都只关注了如何获得刚度低、承载能力大的特性,而没有考虑装置中柔性元件自身振动对载荷的干扰;尤其是振动试验中,在关键的频率范围内柔性元件自身振动被激发而影响载荷的响应,不利于微重力模拟[14];并且已有的准零刚度悬吊装置可调性低,通常适用于质量不变的情况。
为了使悬吊装置既有低刚度、大承载能力的特性,又能避免自振对载荷的干扰,本文利用准零刚度技术,在考虑柔性元件自身振动因素的基础上,设计了一种准零刚度悬吊装置。首先,推导了装置中柔性元件的自振频率计算式,为弹簧设计提供指导,并分析了装置工作原理,得到设计参数应满足的条件;然后,基于试验需求和上述分析结果提出设计流程,进行机械结构设计,得到适用于实际情况的准零刚度悬吊装置;最后,通过静力试验和悬吊-隔振试验,验证了该悬吊装置的主要设计技术目标。
1 准零刚度悬吊装置理论分析
三弹簧并联形式是由Carrella[15]提出的一种获得准零刚度特性的常见方法,本节对该形式的悬吊装置作重点分析。
1.1 弹簧自振频率分析
三弹簧并联形式的悬吊装置如图1所示,包括1根悬吊弹簧与2根侧弹簧,主要用以承受载荷重力。在装置中,两侧弹簧受压,使得在竖直方向上产生负刚度,以抵消悬吊弹簧的正刚度。当装置悬吊载荷并使侧弹簧处于水平位置时,则视为达到静平衡,此时重力载荷由悬吊弹簧承受。
弹簧自振包括悬吊弹簧和侧弹簧的自振。其中侧弹簧是压簧,质量比悬吊弹簧小很多,自振频率高于悬吊弹簧,因此在设计准零刚度悬吊装置时只分析悬吊弹簧的自振频率,使其超过试验关键频率段以避免干扰。悬吊弹簧上端的边界条件为固支,下端的边界条件因侧弹簧质量远小于载荷质量可考虑为只与载荷相连。
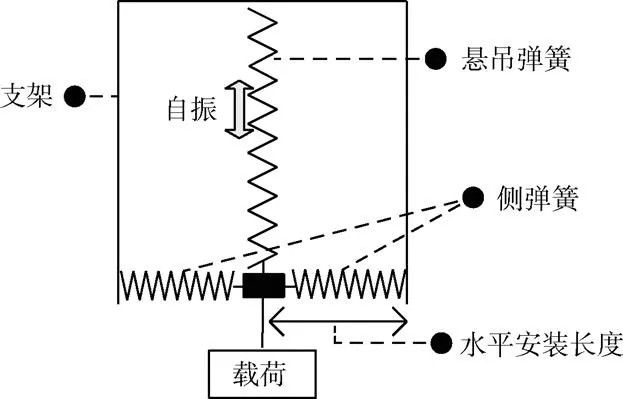
图1 准零刚度悬吊装置示意图
为了便于分析自振频率,将悬吊弹簧等效为质量、刚度相同的均匀弹性杆,如图2所示。
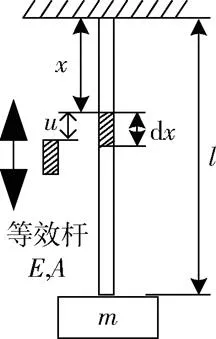
图2 等效杆示意图
载荷质量为;悬吊弹簧的刚度为1,质量为s,自振频率为re;等效弹性杆长度为,密度为,杨氏模量为,截面积为,则有如下关系式:
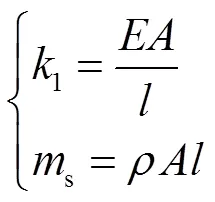
用结构动力学中弹性杆纵向振动的分析方法可得到其振动方程为
(2)
式中:1、2、3和4是积分常数;;为振动角频率。边界条件可表示为

把式(2)代入式(3)中,可得到关于的方程为
。 (4)
由方程(4)可以求得等效杆的自振固有频率。考虑到s,可近似认为方程(4)右边等于0,于是等效杆振动的第一阶角频率可表示为
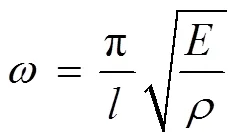
换算成以Hz为单位的表达式,并把式(1)代入式(5),得到弹簧自振频率为
。 (6)
式(6)表明,通过适当近似,悬吊弹簧自振频率可由其刚度与质量估算。利用该结论,并结合弹簧设计方法,可设计悬吊弹簧使其自振频率超过试验的关键频率段,从而避免自振干扰试验结果。
1.2 准零刚度悬吊装置工作原理
三弹簧并联形式的悬吊装置设计参数包括悬吊弹簧刚度1,侧弹簧刚度2、原长0及其水平时的长度。装置承受载荷重力同时受到外力作用,如图3所示。

图3 准零刚度悬吊装置受力图
装置只承受载荷重力并使侧弹簧受压且处于水平状态,悬吊弹簧变形后的位置视为静平衡位置。以静平衡位置为原点,当载荷受到外力作用,将产生位移,则有
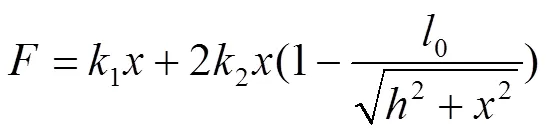
为了便于分析,把式(7)无量纲化为
, (8)

表示悬吊装置刚度与悬吊弹簧刚度的比值。
令=0,=0,得到满足准零刚度条件的和的关系为

不妨令=2/3,则满足准零刚度条件的刚度比z=1。对于不同的,装置的无量纲力-位移曲线与刚度特性曲线见图4。可以看到,当=1.5>z时,装置在=0附近的刚度为负。当=0.5<z时,装置在=0附近表现为正刚度。当=1=z时,装置在=0处刚度为0,悬吊弹簧的正刚度与侧弹簧产生的负刚度刚好抵消。此时,在=0附近一定位移范围内,装置的力-位移曲线几乎呈水平状态,刚度很小。因此在这段位移范围内装置可被认为具有准零刚度特性。
(a) 无量纲力–位移曲线
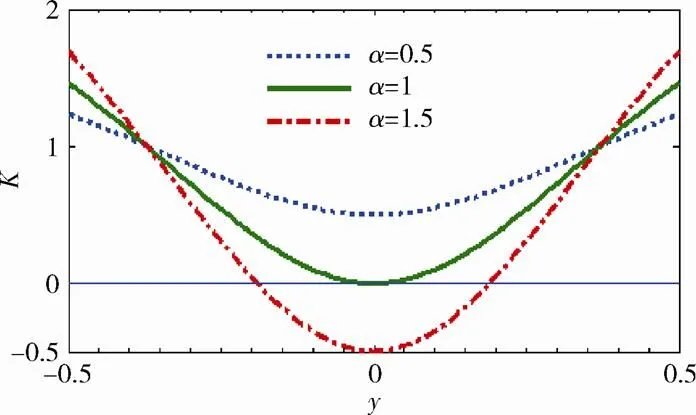
(b) 无量纲刚度–位移曲线
定义0为装置具有准零刚度特性时无量纲刚度的上限值,令0=0.1,把≤0时装置的位移范围作为准零刚度特性位移范围,并希望该范围尽可能的大以满足试验位移需求。而满足准零刚度条件的、组合决定了准零刚度特性位移范围的大小,如图5所示。
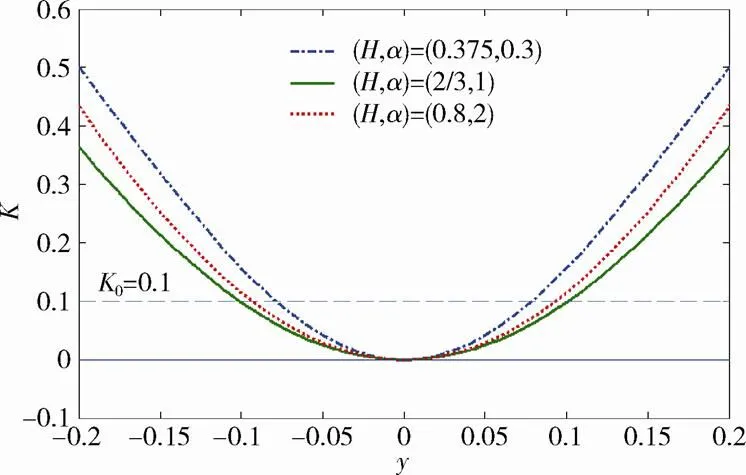
图5 不同Н、α组合下准零刚度悬吊装置的无量纲刚度-位移曲线
通过对准零刚度特性位移范围求最大值,可以确定最佳的、组合。把式(10)代入式(9),并令=0,反解出,则有
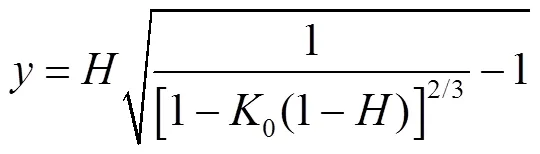
式(11)右边关于的导数等于0,即可求出最大时对应的取值。但鉴于求解的方程很复杂,可以把式(11)关于0泰勒展开得到近似表达式,因0是一个小值,可只保留常数项与一阶项,则得:
。 (12)
对于式(12)易求解,当=2/3时,取最大值,此时为1。按照该、组合所表示的关系对设计参数取值,可得到具有最大准零刚度特性位移范围的悬吊装置。
2 准零刚度悬吊装置设计
由以上分析可知,合理的悬吊弹簧自振频率re可避免载荷受到干扰,满足特定关系的设计参数可使装置具有准零刚度特性。为此,基于试验需求提出以上参数的设计流程,利用自振频率计算式与、的最佳取值,确定以上参数的取值。然后据此进行具体机械结构设计,得到准零刚度悬吊装置。
2.1 参数取值
隔振试验在20Hz以内依靠主动隔振来实现振动衰减,而主动隔振的有效性需在微重力环境下进行检验。为避免悬吊装置在20Hz以内自振干扰试验结果,悬吊弹簧自振频率re应超过20Hz,保险起见,设计时要求re>100Hz。试验中,载荷在竖直方向上的振动位移不超过10mm,因此要求悬吊装置的准零刚度位移范围>10mm。载荷质量为28kg,由3个悬吊装置承受,考虑到装置应具有较大承载力,要求每个装置在承受9.3kg载荷时悬吊弹簧变形不超过30mm。
按照以上要求,确定参数取值,流程如下:
1)利用式(6)和弹簧设计方法得到刚度1和自振频率re都满足要求的悬吊弹簧;
2)由刚度比的最佳取值计算得到侧弹簧的刚度2;
3)将几何参数的最佳取值和给定的0代入式(11)计算得到无量纲的准零刚度位移范围,按照实际位移>10mm的要求确定侧弹簧原长0;
4)根据侧弹簧原长0和几何参数确定侧弹簧的水平长度。
需注意的是,侧弹簧在水平状态时压力不能过大,否则会导致安装困难。以上过程总结为流程图见图6。
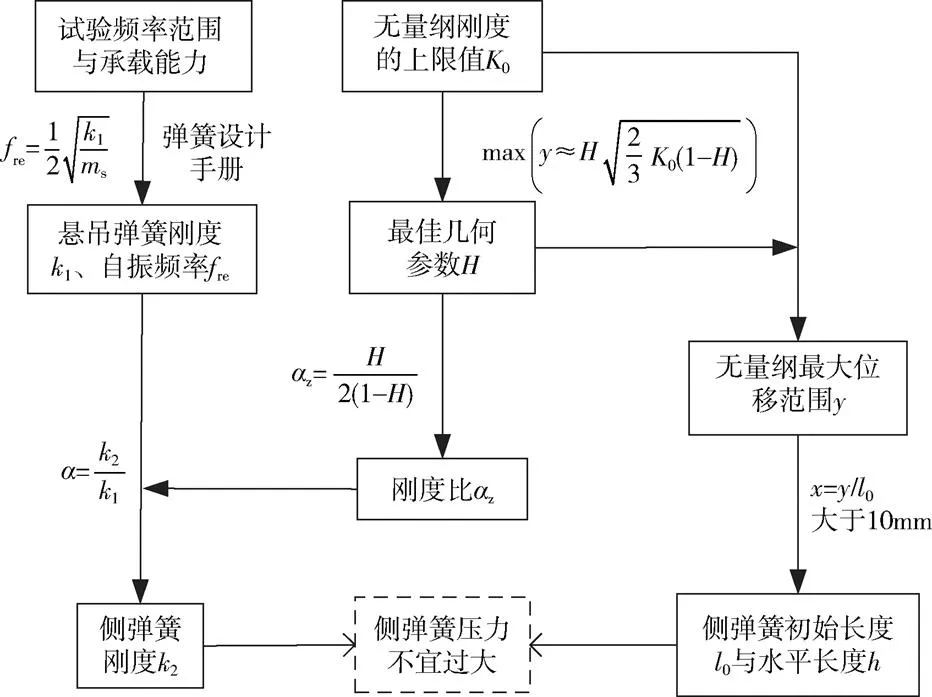
图6 参数设计流程
完成参数取值后,计算发现,侧弹簧水平受压时的压力过大。为减小压力,在三弹簧并联形式的悬吊装置中增加1对侧弹簧,即4个侧弹簧在悬吊弹簧周围呈90°夹角对称分布,见图7。

图7 改进后的准零刚度悬吊装置示意图
改进后的装置与原装置原理相同,只有准零刚度条件下的与关系变为
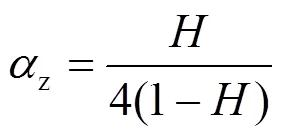
其余参数关系均不变。此时与的最佳取值分别为2/3与1/2。最后得到参数取值见表1。
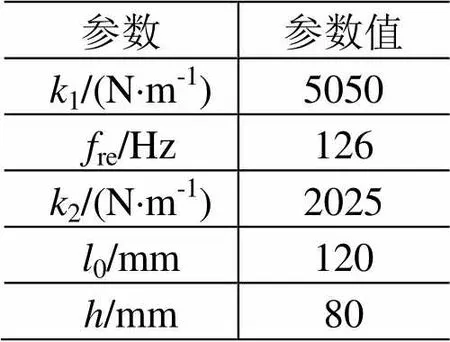
表1 装置参数取值
悬吊弹簧与侧弹簧由碳素弹簧钢丝制成,具体参数见表2。
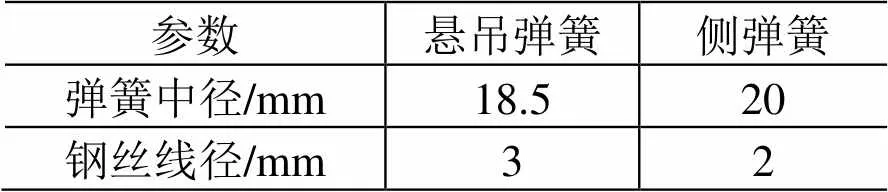
表2 弹簧参数取值
表2(续)
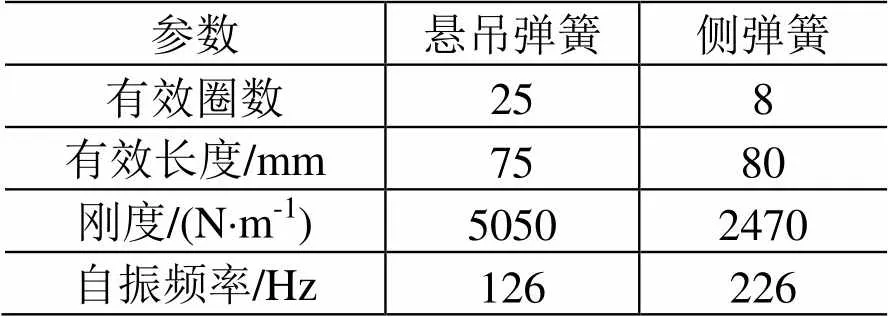
参数悬吊弹簧侧弹簧 有效圈数258 有效长度/mm7580 刚度/(N×m-1)50502470 自振频率/Hz126226
2.2 机械结构设计
根据以上参数取值完成机械结构设计。由前文可知,要求准零刚度悬吊装置承载达静平衡时侧弹簧应处于水平状态,且刚度比与几何参数要满足特定关系。而在实际应用中,装置需承受不同质量的载荷,以及存在安装、加工误差,使得装置不能总是满足上述条件。因此在设计时需加入静平衡位置与几何参数的调节机构,以增强装置的适用性。装置采用了双螺母与螺杆的配合来调节静平衡位置,并通过改变侧弹簧压缩量来调节几何参数。此外,考虑到侧弹簧受压可能失稳的问题,装置中还加入了导向部件。最后得到的装置如图8所示。

图8 准零刚度悬吊装置三维模型
3 试验结果
为验证设计得到的准零刚度悬吊装置是否达到预期目标,通过静力试验来验证装置的准零刚度特性与承载能力,以及通过悬吊-隔振试验来检验装置是否避免了自振对载荷的干扰。
3.1 静力试验结果
静力试验采用RGM-3100型试验机,通过位移加载得到力-位移曲线。准零刚度悬吊装置在试验机上的安装状态见图9。
为使准零刚度悬吊装置在隔振试验中适用于9.3kg的载荷,需调节装置的平衡位置,使装置达静平衡时侧弹簧刚好处于水平状态。进而调节几何参数,使装置在平衡位置附近具有准零刚度特性。调节几何参数前、后的试验结果见图10。

图9 准零刚度特性测试状态

图10 几何参数调节前、后的力-位移测试曲线
因悬吊弹簧有预紧力以及侧弹簧最初有一定压缩量,装置从初始状态开始变形需要预拉力。调节几何参数前,侧弹簧压力较小,提供的负刚度不足以抵消悬吊弹簧的正刚度,因此悬吊装置在平衡位置附近的刚度为正。调节几何参数,增加侧弹簧压缩量,装置从正刚度变为准零刚度。进一步增加侧弹簧压缩量,装置变为负刚度。从图10可看出,装置具备准零刚度特性时,对应的位移范围约为11.17mm,刚度在84N/m以内,承载9.27kg所产生的变形量为19.64mm。这表明该装置达到了低刚度和较大承载能力的设计目标,且可用于悬吊-隔振试验。
3.2 悬吊-隔振试验系统
为检验准零刚度悬吊装置是否能避免自振干扰载荷,本文搭建了悬吊-隔振试验系统。该系统包括悬吊装置、隔振台和激振台。悬吊装置分别采用准零刚度悬吊装置和原普通弹簧,以作对比。隔振台与激振台均为Hexapod结构形式,见图11。
激振台施加竖直方向上的振动。隔振台下板受到振动激励,进行主动隔振控制,使隔振台上板(即载荷)受到的振动衰减。悬吊装置卸载隔振台上板的重力,以模拟失重状态。试验系统如图12所示。

图11 隔振平台与激振台

图12 试验系统示意
3.3 悬吊-隔振试验结果
激振台施加竖直方向上幅值恒为10m的正弦扫频加速度激励,频率为2~20Hz。进行隔振控制,通过隔振台上、下板的加速度计测量隔振效果。试验结果见图13,虚线和实线分别是采用原普通弹簧和准零刚度悬吊装置时的振动传递率幅频曲线。
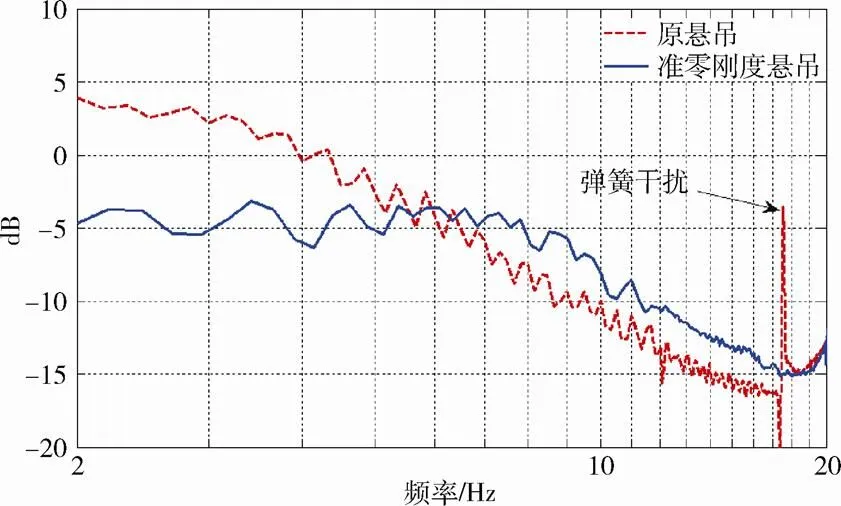
图13 两种悬吊装置的试验结果对比
从试验结果可以看出,使用原弹簧时,隔振效果在17Hz处受到较大的干扰;而采用准零刚度悬吊装置后,则没有干扰。对比整个隔振效果,使用准零刚度悬吊装置时,6Hz之前的隔振效果较好,6Hz之后隔振效果稍差一些。这是因为准零刚度悬吊装置受到尺寸限制,难以做到在整个试验过程中刚度均低于普通弹簧。不过总的看来,悬吊装置带来的影响是可以接受的,与此同时它解决了承载力和弹簧自振干扰的问题。此外,悬吊上板时,原弹簧伸长450mm左右,而准零刚度悬吊装置伸长约19.7mm,变形量大大减小。
4 结论
为了在微重力模拟中,使悬吊装置既能避免弹簧自振对载荷的干扰,又具备低刚度、大承载能力的特性,本文在分析了弹簧自振的基础上,基于准零刚度技术设计了一种准零刚度悬吊装置,最后通过试验验证得到以下结论:
1)按照设计流程得到的准零刚度悬吊装置的刚度、承载能力和位移范围均满足试验需求,有较强的适用性。
2)采用以上设计的准零刚度悬吊装置进行隔振试验,在关键频率段内装置不再干扰载荷的响应,能较好地模拟微重力状态。
(References)
[1] 从强. 空间机构地面重力补偿设备跟踪研究[J]. 航天器环境工程, 2012, 29(1): 92-99
CONG Q.An investigation into gravity compensation equipment for space mechanisms[J].Spacecraft Environment Engineering, 2012, 29(1):92-99
[2] 路波. 零重力环境模拟气动悬挂系统的关键技术研究[D].杭州: 浙江大学,2009: 21-22
[3] ALABUZHEV P M, RIVIN E I. Vibration protection and measuring systems with quasi-zero stiffness[M]. London: Hemisphere Publishing, 1989
[4] 徐道临, 成传望, 周加喜. 屈曲板型准零刚度隔振器的设计和特性分析[J]. 湖南大学学报(自然科学版), 2014, 41(8): 17-22
XU D L, CHENG C W, ZHOU J X. Design and characteristic analysis of a buckling plate vibration isolantor with quasi-zero-stiffness[J].Journal of Hunan University(Natural Sciences), 2014, 41(8):17-22
[5] 孟令帅, 孙景工, 牛福, 等. 新型准零刚度隔振系统的设计与研究[J]. 振动与冲击, 2014, 33(11): 195-199
MENG L S, SUN J G, NIU F, et al. Design and analysis of a novel quasi-zero stiffness vibration isolation system[J]. Journal of Vibration and Shock, 2014, 33(11):195-199
[6] 徐道临, 赵智, 周加喜. 气动可调式准零刚度隔振器设计及特性分析[J]. 湖南大学学报(自然科学版), 2013, 40(6): 47-52
XU D L, ZHAO Z, ZHOU J X. Design and analysis of an adjustable pneumatic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Hunan University(Natural Sciences), 2013, 40(6):47-52
[7] XU D L, YU Q P, ZHOU J X, et al. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2013, 332(14): 3377-3389
[8] 董光旭, 罗亚军, 严博, 等. 基于正负刚度并联的低频隔振器研究[J]. 航空学报, 2016, 37(7): 2189-2199
DONG G X, LUO Y J, YAN B, et al. Study on a low frequency vibration isolator based on combined positive and negative stiffness[J]. Acta Aeronautica ET Astronautica Sinica, 2016, 37(7): 2189-2199
[9] GOLD R R, FRIEDMAN I P, REED III W H, et al. Suspension systems for ground testing large space structures: NASA CR1990-4325[R]. VA: Langley Research Center
[10] ROGERS L C, RICHARDS K E. PACOSS program overview and status[C]//NASA/Dept of Defense Control/Structures Interaction Technology Conference. Norfolk, VA, 1986:85-109
[11] HARVEY T J. Adjustment of zero spring rate suspensions:US,5024111[P], 1991-6-18
[12] CRAWLEY E F. Very low frequency suspension systems for dynamic testing[C]//30thStructures, Structural Dynamics and Materials Conference, 1989: 1194
[13] WOODARD S E, COOLEY V M. NASA CSI suspension methods overview[C]//NASA/Dept of Defense Control/Structures Interaction Technology Conference. San Diego, California, 1989: 317-333
[14] 齐乃明, 张文辉, 高九州, 等. 空间微重力环境地面模拟试验方法综述[J]. 航天控制, 2011, 29(3): 95-100
QI N M, ZHANG W H, GAO J Z, et al. The primary discussion for the ground simulation system of spacial microgavity[J]. Aerospace Control, 2011, 29(3): 95-100
[15] CARRELLA A, BRENNAN M J, WATERS T P. Static analysis of a passive vibration isolator with quasi- zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2007, 301(3): 678-689
(编辑:肖福根)
Design and experiment of a suspension device based on quasi-zero-stiffness technology for microgravity simulation
TANG Rui1, HUANG Hai1, HUANG Zhou2
(1. School of Astronautics, Beihang University, Beijing 100191, China; 2. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China)
The microgravity simulation on the ground is an important step to improve the on-orbit reliability of spacecraft. The low-stiffness suspension device is usually employed in the microgravity simulation, which results in the low bearing capacity of the device and the interference from the device’s vibration. With this problem in mind, a quasi-zero-stiffness suspension device with consideration of its own vibration is designed in this paper. Firstly, the expression for the frequency of the bearing spring is derived by ignoring secondary factors. The conditions for the main parameters are discussed in a principle analysis. After that, a design procedure is proposed according to the payload mass and the displacement in the experiment. A quasi-zero-stiffness suspension device is thus designed, that can adjust the equilibrium position and the geometry parameter. A static testing and a vibration isolation experiment using the suspension device are conducted. It is shown that with this suspension device, the quasi-zero-stiffness and a high bearing capacity can be secured, and the interference from its vibration can be eliminated.
microgravity simulation; quasi-zero-stiffness; suspension device; natural frequency disturbance; structural design
V416.5
A
1673-1379(2017)02-0222-07
10.3969/j.issn.1673-1379.2017.02.019
2016-08-03;
2017-03-05
唐锐(1991—),男,硕士研究生,研究方向为航天器结构设计与分析;E-mail: tangrui86377627@126.com。指导教师:黄海(1963—),男,教授,研究方向为飞行器结构优化,空间智能结构及其控制等;E-mail: hhuang@buaa.edu.cn。
http://www.bisee.ac.cn
E-mail: htqhjgc@126.com
Tel: (010)68116407, 68116408, 68116544

