乒乓球拍海绵特性碰撞动 力学分析

谢聪锋，李 春

乒乓球拍海绵特性碰撞动 力学分析

谢聪锋，李 春

海绵是乒乓球拍的重要组成部分，其硬度和厚度直接决定了球的速度、旋转及控制效果。为研究乒乓球拍中海绵厚度对乒乓球运动状态的影响，基于显式动力学理论并结合有限元方法，通过ANSYS Workbench对考虑旋转的乒乓球与球拍碰撞模型进行数值模拟，对比分析了球拍材质相同情况下不同海绵厚度对乒乓球运动状态及球拍最大压缩量的对应关系。结果表明：乒乓球反射速度随海绵厚度的增加急剧减小而后缓慢增大，且球反射速度随入射角度的增大而减小；球拍的最大压缩量随海绵厚度的增加而增大，且随入射角的增大而增大；乒乓球反射速度随入射角度的增大呈减小趋势。

乒乓球；显式动力学；碰撞；海绵

乒乓球是一项集速度、力量、落点、旋转、线路和节奏于一体的体育运动［1，3，18］。乒乓球也一直被誉为“国球”，除群众基础雄厚之外，还因中国乒乓球运动员在世界大赛中多次获得冠军。2016年8月18日，里约奥运会马龙率领中国男队3-1战胜日本队获男团冠军，中国队成功包揽了本次奥运会男单（马龙）、女单（丁宁）以及男、女团体4枚金牌。这是中国乒乓球队继1996年亚特兰大奥运会、2000年悉尼奥运会、2008年北京奥运会及2012年伦敦奥运会后，历史第5度在单届奥运会上包揽乒乓球项目4枚金牌［2］。这些成绩的取得不仅与运动员刻苦训练、顽强拼搏有关，还与体育科研人员对每一项技术的深入研究息息相关。随着计算机仿真技术的发展，使得对乒乓球运动进行理论研究成为可能［16］。

近百年来，乒乓球拍经历了由用羔皮纸贴成的长柄椭圆形空心球拍到木板拍，又由木板拍到呢绒拍、羊皮拍、胶皮拍，再到海绵拍和正、反胶海绵拍及各式各样球拍的发展和变革过程，而乒乓球拍的每一次变革，都曾引起各种新技术的产生与发展。有关乒乓球的研究，国内学者已作了一些定性分析，对于一些基本规律也提出许多阐述，但尚有大量问题有待通过定量研究来深入认识［19］。

Nakashima等［26］基于空气动力学模型，通过中速摄像机测得乒乓球的运动轨迹，提出了一种乒乓球旋转速度和运动速度的估测方法，并采用数值模拟进行了验证；Liu等［25］基于球拍反弹模型和空气动力学模型，通过求解非线性方程组，求解两点微分方程的边值问题，预测乒乓球击球点和转速，从而为控制乒乓球机器人手臂挥拍运动提供依据。通过数值模拟并与实验结果对比证明了方法的可靠性；Zhang等［27］假设平行于接触平面的两个方向上的速度在碰撞前后呈线性关系，在碰撞平面的法线方向上，利用弹性恢复系数得到碰撞后的反弹速度；武秀根等基于商用有限元软件MSC.MARC，通过乒乓球与球拍碰撞过程的数值模拟，着重研究了由传统木材和碳纤维复合材料板叠合而成的乒乓球拍微结构对碰撞后乒乓球运动规律的影响［12］，此外，还研究分析了球拍中加入碳纤维含量对球速的影响；林小兵通过调查研究与多年的教学实践，论证了乒乓球拍海绵硬度（H值）对快弧选手技术水平的影响，初步建立了快弧选手技术水平与海绵硬度（H值）之间的定量关系［4］；王吉生阐述了不同底板、海绵及胶皮等优化组合的独特性能，给出了不同技术打法与特定搭配乒乓球拍间的关系［13］。

海绵作为影响乒乓球拍综合性能的重要组成部分，其物理性质及材料几何参数对乒乓球运动影响的定量研究，却鲜有国内、外研究人员提及。

1952年，第19届世界乒乓球锦标赛中，日本运动员佐藤博治首次在球拍中使用了一块厚度为8 mm的软海绵，这薄薄一层海绵的加入使球拍极大地增加了击球力量和速度。正是凭借对球拍器械的技术创新，日本队在该届比赛中一举获得女团、男单、男双、女双等4项冠军。同时，日本队使用海绵拍取得的辉煌成绩，也颠覆了欧洲运动员削球打法的统治地位，使得亚洲乒乓球步入了“黄金期”。随后，国际乒联充分肯定了海绵拍对乒乓球运动的积极意义，从此乒乓球运动进入追求力量和速度的时代［17］。

海绵是乒乓球拍的重要组成部分，其硬度和厚度直接影响了球的速度、旋转和控制效果［5，20］。一方面，海绵特性对乒乓球的运动状态影响较大；另一方面，实验研究不仅存在费用高、周期长和精度受限等问题，且有些实验研究无法全面反映实际情况，诸如乒乓球与球拍的接触时间仅为千分之一秒，这对压力传感器提出了极高的要求，目前用于商业化的压力传感器存在动态性能差、精度受限等问题，无法满足实验要求。因此，数值模拟自然成为研究海绵特性的重要方法。本文基于ANSYS Workbench显式动力学，通过对乒乓球与球拍碰撞过程的数值模拟，对比分析了球拍材质及底板和胶皮厚度相同情况下不同海绵厚度对乒乓球运动状态、球拍最大压缩量的影响。

1 研究对象

海绵是一种微孔橡胶制品，经过发泡工艺而产生的无数个密闭小孔布满其内，从而形成了众多的微型气室［6］。当受到来球撞击时，与触球点临近的气室受力收缩，海绵由此产生形变而凹陷：一方面，使乒乓球在海绵上有“滞止”的瞬间接触时间，俗称将来球“吃”住。这一特征为运动员调节击球用力、方向和时机提供了可能，尤其是对于专业运动员，该瞬间接触时间显得异常重要；另一方面，在“滞止”的瞬间接触时间内，由于海绵形变所产生的弹性势能，转化为对球作用力，增加了球的反弹动能，进而提高了球的速度，它为增强击球力量和优化弧线提供了条件。因此，可以认为海绵的作用主要体现在控制球和提高击球速度上［5］。

目前，国内市场上的乒乓球拍海绵主要有3类，即国产海绵、日本海绵和德国海绵（表1）［16］。

表1 不同产地海绵性能Table 1 Performance of Sponge from Different Producing Areas

2 理论基础

2.1 显式动力学有限元法

动态显式算法是采用动力学方程的一些差分格式（如中心差分法、线性加速度法、Newmark法和Wilson法等），该算法不用直接求解切线刚度，也不需要进行平衡迭代，计算速度快。当时间步长足够小时，一般不存在收敛性问题。动态显式算法需要的内存比隐式算法要少，同时数值计算过程可较容易地进行并行计算，程序编制也相对简单。显式算法要求质量矩阵为对角矩阵，且只有在单元级计算尽可能少时速度优势才能得以充分发挥，因而往往采用减缩积分方法，但容易激发沙漏模式，影响计算精度［7］。

传统有限元法属于静态隐式算法，求解中每个时间步都要重新计算大型非线性刚度矩阵，并进行反复迭代获得收敛解，需要的计算时间较长且存储空间较大。不同于隐式算法，显式动力学有限元法无须建立刚度矩阵和求逆运算，而是采用中心差分法显式求解有限元方程，并通过单点高斯积分和集中质量，提高了求解速度，具有节省计算时间和存储空间的优点。近年来，显式动力学有限元法在碰撞冲击领域得到广泛应用，并表现出在处理大规模接触问题上的优势［7，8，14，15］。

2.2 控制方程

ANSYS/LS-DYNA是世界上最著名的通用显式非线性有限元分析程序，以求解二维、三维结构碰撞和金属成型等非线性动力冲击问题为主［21］。在动力学有限元分析系统中，碰撞运动方程可表示为：

式中： M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；a为加速度矢量；v 为速度矢量；d 为位移矢量；F 为包括碰撞力在内的外力矢量。

考虑数值模拟系统的沙漏能效应，系统控制方程变为：

式中：H为沙漏力。

2.3 碰撞过程机理及分类

碰撞可简单分为压缩和恢复两个过程。在碰撞过程中，两物体之间发生了随时间变化的碰撞力作用，并导致了碰撞过程中能量交换和碰撞物体运动速度改变。碰撞动力学研究就是要从碰撞物体材料参数与碰撞前物体速度出发，确定碰撞后物体速度变化。在碰撞动力学模型分析中，这类研究分为两种，即“刚球模型”与“软球模型”。刚球模型是应用经典力学理论，将碰撞体按刚体进行处理而不考虑上述两个过程的细节关系；软球模型则需要按变形体来建立碰撞挤压力与挤压变形之间的关系式，给出碰撞接触力。按照碰撞过程能量的变化，我们一般将物体间的碰撞分为3种形式：1）完全弹性碰撞，就是两物体在碰撞过程中没有能量损耗；2）完全塑性碰撞，即在碰撞过程中没有弹性，碰撞的能量转化形式只有动能和系统内能之间的转换；3）弹塑性碰撞，介于完全弹性碰撞和完全塑性碰撞之间，它经历了碰撞的挤压阶段与恢复阶段，但在恢复阶段中储存在系统中的变形能没有全部转换为动能［11］。

3 数值模拟

3.1 几何模型

使用Unigraphics NX 9.0对乒乓球及球拍进行三维几何建模，球拍分3层，即底板、海绵和胶皮。本应以海绵为主要研究对象，但考虑到模拟对象与结果的真实有效性，建模时在球拍上布置一层底板和胶皮（反胶）。由于击球过程中只有球拍一侧的胶皮和海绵对乒乓球运动状态有影响（不考虑国人发明的直拍反打技术）。因此，几何建模中只建立球拍一侧的底板、胶皮层和海绵层。参照国家标准［10］，底板厚度设为6 mm，胶皮1.5 mm，海绵0.3～0.9 mm以0.1 mm为间隔取7组，0.9～2.7 mm并以0.3 mm为间隔取6组，共13组厚度［16］，乒乓球采用大球尺寸标准外半径20 mm，内半径19.61 mm［9］。

3.2 材料属性

乒乓球拍底板中的木质材料和乒乓球所使用的赛璐珞均为各向异性材料，但是，它们相对于胶皮和海绵，在碰撞过程中形变很小，故将其均设为各向同性材料。材料的机械性能参数如表2所示［22，23］。

3.3 网格划分

选择网格类型为显式（Explicit），整体单元大小为5 mm，对乒乓球拍插入尺寸（Sizing），局部细化球拍网格，确定影响区的球半径为40 mm，单元大小为2 mm，如图2所示，共划分成18 292个节点，12 598个单元。

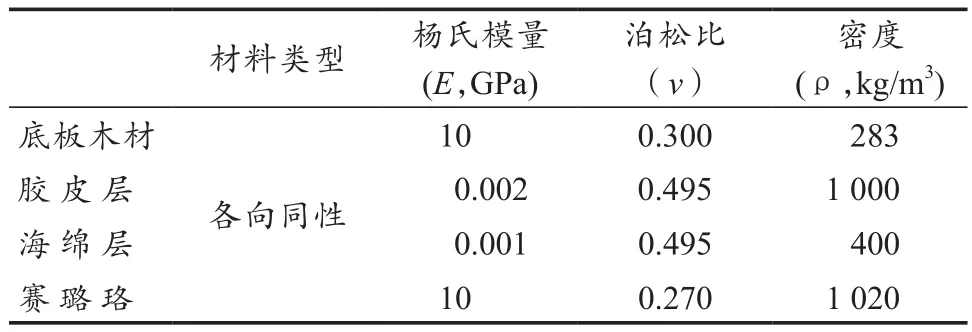
表2 材料机械性能参数Table 2 Mechanical Properties of Materials

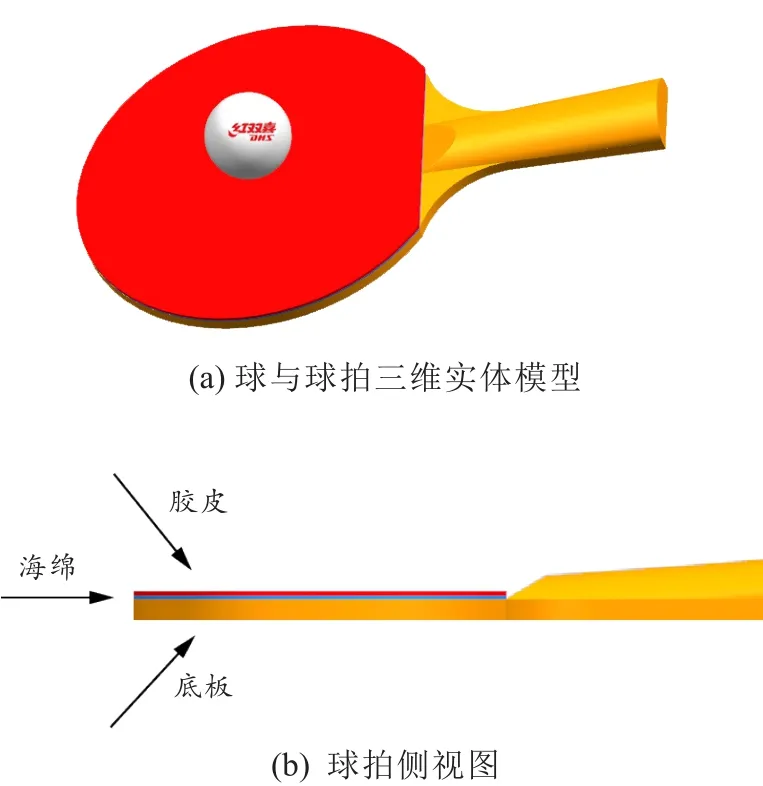
图1 球拍实体模型与侧视图Figure 1 Model of Racket and the Side View

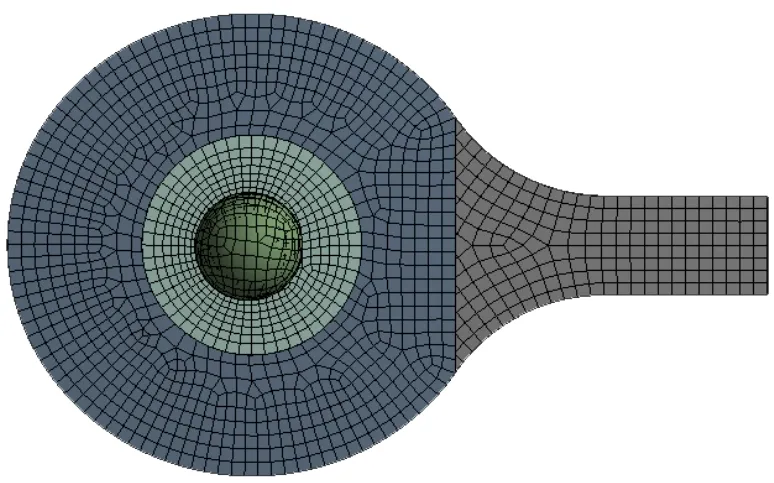
图2 球拍网格分布Figure 2 Mesh Distribution

3.4 边界条件

采用边界条件为球拍手柄固定，用于模拟击球时拍柄被手紧握的实际情况。分别考虑了乒乓球以30°、45°和90°3种入射角度撞击不同海绵厚度的球拍。不失一般性，设球的初始速度在y、z平面内，乒乓球入射角α和反射角β的定义如图3所示。

以击球时球拍与球之间的相对速度作为球初始速度，用球心速度v表示。球与球拍间相对速度为v0＝20 m/s，球自身转动速度为下旋球ω0＝50 rad/s［19，20］。取球与球拍胶皮的摩擦系数 μ＝1.2，本文主要研究乒乓球与拍面的碰撞过程，空气阻力对此影响不大，因此忽略不计［12］。

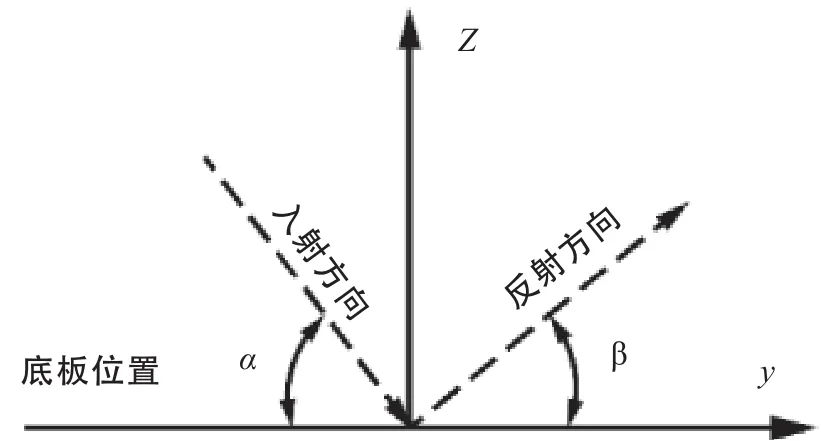
图3 乒乓球入射角和反射角Figure 3 Incident Angle and Reflex Angle

4 结果与分析

4.1 乒乓球与球拍碰撞过程

球拍与乒乓球开始接触时，胶皮层因受到球的挤压而内凹变形，该碰撞力传递到海绵层使之也发生类似形变。随着胶皮层和海绵层变形的增大，球受到的阻力也逐渐增大，速度急剧减小，球由于摩擦作用而受到的剪力逐渐增大。剪力的存在对球旋转产生了影响，改变了转动速度。当球与球拍间的相对速度达到零后，胶皮层与海绵层的变形逐渐恢复，球与球拍开始逐渐脱离，球受到的剪力逐渐减小，直至球以新的速度矢量和转速与球拍完全分离，此时球具有转动和平动两种运动形式。图4为乒乓球以90°入射角撞击海绵厚度为1.2 mm球拍时速度的变化过程。

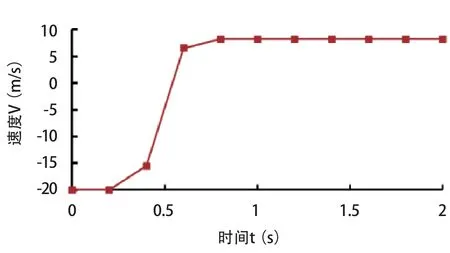
图4 乒乓球与球拍碰撞过程Figure 4 Collision Course between Table Tennis and Racket

4.2 数值模拟结果有效性验证

图5显示了海绵厚度为1.2 mm，乒乓球垂直碰撞时整个碰撞系统动能、内能和沙漏能随时间的变化情况。如图所示，球体动能在碰撞后迅速下降并最终趋于稳定，同时系统内能随之增加。需要特别指出的是，沙漏模态是一种以比全局响应高得多的频率振荡的零能变形模式，它在数学上是稳定的，但在物理上是不可能发生的，如果总的沙漏能大于系统内能的10%，这个分析很有可能是失效的［24］。由图5可知，模拟系统的沙漏能约为1 kJ，远低于内能的1%，因此，数值模拟结果是令人满意的。

4.3 海绵厚度对乒乓球运动状态的影响

固定球拍材质及底板和胶皮厚度不变，考虑乒乓球分别以30°、45°和90°入射角撞击同一厚度海绵的球拍；同一入射角度，共取13组海绵厚度进行计算，分别为：0.3～0.9 mm以0.1 mm为间隔取7组，0.9～2.7 mm以0.3 mm为间隔取6组。不同海绵厚度的乒乓球拍对碰撞后球反射速度的影响如图6所示。

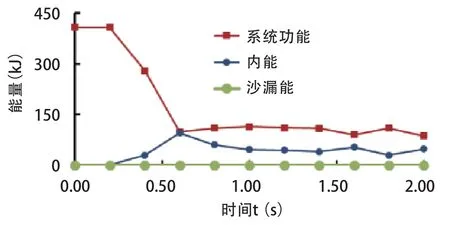
图5 乒乓球垂直碰撞时系统碰撞能量曲线Figure 5 The Curves of Impact System Energy

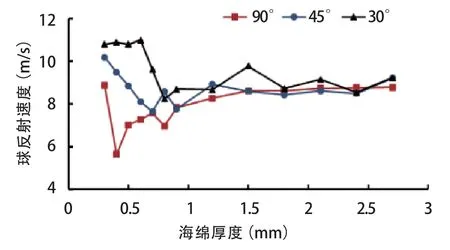
图6 不同海绵厚度对乒乓球反射速度影响Figure 6 Effect of Different Thickness of Sponge on the Reflex Speed of Table Tennis

由图6可知，乒乓球反射速度随海绵厚度的增加急剧减小而后缓慢增大，且随入射角度的增加而减小。当入射角为90°时，碰撞结束后球的速度V随海绵厚度的增大先减小，在厚度为0.4 mm左右达到最小值，而后随海绵厚度的增大而增大；当厚度为0.7 mm左右时，球速再次减小，厚度增至0.8 mm后，球速随厚度的增加而增大，但增大的趋势并不明显。当入射角为45°时，球速随海绵厚度的变化与90°入射角具有类似的趋势，但速度突变点相对略有延后，同时反射速度整体高于后者。当入射角为30°时，亦是如此。

由此可总结出乒乓球碰撞后运动状态随海绵厚度变化的规律，但从理论上讲，海绵越厚，弹性越大，而实际上来球的撞击力往往无法穿透过厚的海绵，结果使底板弹性难以得到充分发挥；但海绵过薄，也会适得其反，球尚未最大限度地与球拍接触，即遇到底板的反弹力而弹出，这样既得不到足够的停球时间，又缺乏飞行的后续力量。

同理，固定球拍材质及底板和胶皮厚度不变，考虑乒乓球分别以30°、45°和90°入射角撞击同一厚度的海绵球拍；同一入射角度，0.3～2.7 mm以0.3 mm为间隔共取9组海绵厚度分别进行计算，研究海绵厚度对乒乓球拍最大压缩量的影响(图7)。

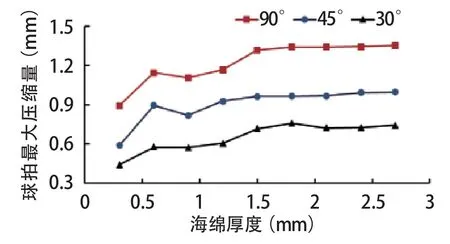
图7 海绵厚度对乒乓球拍最大压缩量影响Figure 7 Effect of Different Thickness of Sponge on the Maximum Compression of Table Tennis

由图7可知，当海绵厚度相同时，由于动能更大程度地转化为弹性势能，球拍的最大压缩量(胶皮和海绵的最大形变量之和)随乒乓球入射角度的增大而增大；当入射角度一定时，海绵厚度增大为球拍提供了更大的弹性势能积蓄空间，故最大压缩量随海绵厚度增加而呈现出增大的趋势。

为研究海绵厚度以及入射角度对乒乓球碰撞后反射角的影响，同一乒乓球入射角取9组不同海绵厚度的乒乓球拍，同一海绵厚度取3种入射角度，分别进行计算，其结果如图8所示。

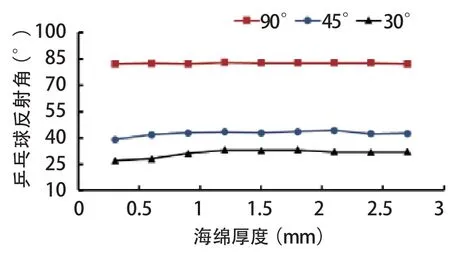
图8 海绵厚度对乒乓球反射角度的 影响Figure 8 Effect of Different Thickness of Sponge on Reflex Angle of Table Tennis

图8所示数据表明，乒乓球反射角受海绵厚度的影响较小，随入射角度的增大而增大。由于乒乓球具有转速及球拍表面胶皮层摩擦系数的存在，球入射角不等于反射角。当入射角为90°时，乒乓球反射角明显大于30°和45°入射角时的情况。

4.4 球入射角度对反射速度的影响

不失一般性，同一入射角度取海绵厚度分别为0.6 mm、1.2 mm和1.8 mm；同一海绵厚度，10°～90°以10°为间隔取9组不同入射角。探究球入射角度与反射速度的关系，结果如图9所示。

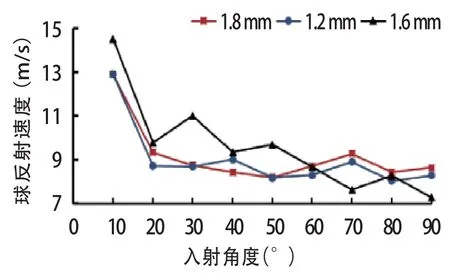
图9 乒乓球入射角度对球反射速度的影响Figure 9 Effect of Incident Angle on Reflex Speed of Table Tennis

由图9所示数据可知，乒乓球的反射速度随入射角度的增加整体呈现出减小的趋势。此结论与图6所示结果相符，验证了仿真结果及图6所得结论的正确性。如图所示，入射角小于20°时，乒乓球反射速度随入射角度的增加急剧减小至8.72 m/s，随后继续下降，但趋势较为平缓。究其原因，球体的入射角度越大，垂直入射的速度分量就越大，更多的动能转化为球拍弹性势能，由此产生的能量损失随之增大，故球体反射速度随入射角度的增大而减小。

5 结论

本文将计算机仿真技术运用到乒乓球与球拍碰撞问题的研究中，基于显式动力学理论并结合有限元方法，通过ANSYS Workbench对考虑旋转的乒乓球与球拍碰撞模型进行数值模拟。固定球拍材质及底板和胶皮厚度不变，考虑乒乓球分别以30°、45°和90°的入射角度撞击同一厚度海绵球拍；同一入射角度，共取13组海绵厚度进行计算，对比分析了球拍材质及胶皮和底板厚度相同情况下不同海绵厚度对乒乓球运动状态及球拍最大压缩量的影响。另外，为探究球入射角度与反射速度的关系，同一入射角度取海绵厚度分别为0.6 mm、1.2 mm和1.8 mm；同一海绵厚度，以10°为间隔取10°～90°共9组不同的入射角度。研究分析后得出如下结论：

1. 海绵厚度小于0.8 mm时，球反射速度随海绵厚度的增加而急剧减小，而大于0.8 mm时，反射速度缓慢增大；且球反射速度随入射角度的增加而减小。海绵厚度在0.8 mm～2.5mm之间弹性适宜，控球效果良好，击球的后续力量较足；

2.球拍最大压缩量随海绵厚度的增大而增大，且随球入射角度的增加而增大。即海绵越厚控球效果越好，但过厚的海绵会增加球拍重量，以0.8～2.7 mm为宜；

3.乒乓球反射速度随入射角度的增大而减小。

［1］ 程序．乒乓球理论与方法［M］．武汉：中国地质大学出版社，2009：20．

［2］ 窦远行．中国乒乓球队历届奥运战绩：里约第5次包揽金牌［EB/O L］．http：//news.sohu. com/20160818/n464841590.shtml.

［3］ 蒋立，张博．乒乓球［M］．北京：人民体育出版社，1997：88．

［4］ 林 小兵．乒乓球拍海绵硬度与快弧选手技术水平的关系［J］．广州体育学院学报，199 6，16(1)：81-84．

［5］ 李相如，魏利婕．乒乓球运动［M］．北京：中央广播电视大学出版社，20 13：10．

［6］ 刘培生．多孔材料引论［M］．北京： 清华大学出版社，2004：163．

［7］ 凌桂龙．ANSYS Workbench 1 3.0从入门到精通［M］．北京：清华大学出版社，2012：68．

［8］ 刘荣昌，马淑英，马国清．曲轴滚压关键 参数设计理论与数值模拟［M］．北京：国防工业出版社，2010：255．

［9］ 林昱．体育 ［M］．南昌：江西高校出版社，2009：66．

［11］ 石富强．两小球弹塑性碰撞 过程的动力学分析及建模［D］．兰州：兰州大学，2011：2-3．

［12］ 武秀根，郑百林，贺鹏飞．乒乓球拍微结构对乒乓球与球拍碰撞过程的研究［J］．体育科研，2006，27(2)：5 9-61．

［13］ 王吉生．如何进行乒乓球底板与海绵胶皮的选择搭配［J ］．乒乓世界，1999，13(4)：36-36．

［14］ 王红岩．空投装备回收系统建模与分析［M］．北京：国防工业出版社，2014：98．

［15］ 王娟．长杆弹侵彻有限直径金属厚靶的理论与数值分析［D］．西安：长安大学，2015：4-77．

［16］ 杨春卉，袁志华，梁振刚．乒乓球反弹动态特性的仿真研究［J］．计算机仿真，2014，31( 10)：281-285．

［17］ 杨桦．乒乓球运动教程［M］．北京： 北京体育大学出版社，2014：46．

［18］ 张红玲．当今乒乓球运动技战 术发展趋势［D］．北京：北京体育大学，2006：14．

［19］ 张惠钦．乒乓球的旋转 ［M］．北京：人民体育出版社，1981：58．

［20］ 张晓蓬，吴焕群．40 mm乒乓球对比赛状态的影响［J］．天津体育学院学报，2000，5(3)：65-66．

［21］ 张乐乐，高祥，谭南林，等．基于ANSYS/LS-DYNA的滚动轴承仿真与分析［J］．机械设计，2007，24(9)：62-65．

［10］ 乒乓球拍(GB/T 23115—2008)［S］．北京：2009．

［22］ 赵渠森．先进复合材料手册［M］．北京：中国标准出版社，机械工业出版社，2003：580．

［23］ 张留成，瞿雄伟，丁会利．高分子材料基础［M］．北京：化学工业出版社，2002：128．

［24］ 张乐乐．ANSYS辅助分析应用基础教程［M］．北京：北京交通大学出版社，2006：268．

［25］ LIU C，HAYAKAWA Y，NAKASHIMA A. Racket control and its experiments for robot playing table tennis［C］// IEEE International Conference on Robotics and Biomimetics. IEEE，2012：266-280.

［26］ NAKASHIMA A，OKAMOTO T，HAYAKAWA Y. An Online Estimation of Rotational Velocity of Flying Ball via Aerodynamics［C］// IFAC World Congress. Cape Town：2014：35-47.

［27］ ZHANG Z，XU D，YANG P. Rebound model of table tennis ball for trajectory prediction［C］// Robotics and Biomimetics (ROBIO)，2010 IEEE International Conference on. IEEE，2010：376-380.

Collision Dynamics Analysis for Characteristics of Sponge in Table Tennis Racket

XIE Cong-feng， LI Chun

Sponge is an important component of the table tennis racket，and its hardness and thickness directly affect the speed，spin and control of the table tennis. In order to study the inf l uence of sponge thickness on table tennis movement state，we compare the inf l uence of rackets with different sponge thickness but the same material to the movement of table tennis and racket maximum deformation by using ANSYS Workbench numerical simulation of collision between racket and spinning table tennis based on explicit dynamic theory and fi nite element method. Conclusions are as follows：table tennis ref l ex speed decreases rapidly with the increase of the thickness of the sponge and then increases slowly，and the ball ref l ex speed decreases with the increase of the incident angle；the maximum amount of compression of the racket increases with the increase of the sponge thickness as well as the incidence angle；table tennis ref l ex speed sh ows a decreasing trend with the increase of incident angle.

table tennis；explicit dynamics；collision；sponge

G804.6

A

1002-9826（2017）03-0140-06

10. 16470/j. csst. 201703020

2016-09-21；

2016-12-14

上海市教育发展基金“晨光计划”项目（13CG55）。

谢聪锋，男，在读硕士研究生，主要研究方向为显式动力学及其仿真，E-mail：15738080105@163.com。

上海理工大学 能源与动力工程学院，上海200093．

University of Shanghai for Science and Technology, Shanghai，200093 China．