埃及裂颜蝠超声辐射波束形成结构的数值研究

庄桥，陈晓乾，张美生

（山东建筑大学理学院，山东济南250101）

埃及裂颜蝠超声辐射波束形成结构的数值研究

庄桥，陈晓乾，张美生

（山东建筑大学理学院，山东济南250101）

智能天线是第三代移动通信系统中不可或缺的关键技术之一，埃及裂颜蝠超声辐射波束形成结构的研究可为智能天线的改进提供理论依据。文章利用时域有限差分法（FDTD）和基尔霍夫积分等数值方法研究埃及裂颜蝠鼻叶组成部分（凹坑、上叶和下叶）对超声辐射波束的影响。运用扫描和图像处理获得鼻叶的三维数字模型，对其组成部分进行剔除得到各种新的鼻叶模型，并对所有鼻叶模型进行数值计算分析，获得不同鼻叶结构的近场声压幅度分布图、远场辐射波瓣图和方向性的相关性系数。结果表明：凹坑不仅可以对近场声场进行聚焦，也会对远场声场的形成和远场辐射的方向性产生影响；上叶对凹坑附近和前方产生的声压幅度进行轻微的调节，下叶起到聚焦的作用；凹坑、上叶和下叶3个部分的不同组合会对辐射波束的形成产生复杂的影响，而这3个部分全被剔除掉的鼻叶结构对声场的分布产生的影响最大，其相关性系数平均值低于0.85。

埃及裂颜蝠；鼻叶模型；超声辐射波束；辐射波瓣图

Key words：Egyptian slit-faced bat；noseleafmodel；emission beamforming；radiation pattern

0 引言

蝙蝠属于翼手目动物，其种类大约有1116种，是哺乳动物中仅次于啮齿目的第二大目，翼手目动物可分为大蝙蝠亚目（173种蝙蝠）和小蝙蝠亚目（943种蝙蝠）。蝙蝠不仅种类丰富，而且数量非常庞大，除寒冷的极地地区和偏远的小岛之外，其在世界各地都有分布。小蝙蝠亚目中的所有蝙蝠和大蝙蝠亚目中果蝠属的蝙蝠能够利用声呐进行回声定位（Echolocation）［1］，具有该功能的蝙蝠种类有953种，为了区别工业和国防中所使用的声呐，将蝙蝠的声呐系统称为生物声呐（Biosonar）。具有回声定位功能的蝙蝠通常用喉部发声，通过鼻孔或嘴发射声信号，然后利用它们的大耳朵接收反射回来的声波，通过大脑对声信号进行分析。根据回声它们不仅能调整飞行方向，还能辨别不同的昆虫或障碍物，进行有效的回避或追捕，借助这一特点，蝙蝠能够在完全黑暗的环境中完成飞行和捕食。

利用鼻孔发射超声信号的蝙蝠，其鼻孔周围通常具有复杂的褶皱结构——鼻叶。鼻叶在作为分类学特征的同时，也对生物声呐波束的形成具有决定性作用［1－5］。在模拟蝙蝠听觉系统和信号发射系统的组合实验中发现，鼻叶能够聚焦能量，并且可以进行选择性的声透射［6－7］。为了探究鼻叶不同组成部分对超声辐射波束的影响，对埃及裂颜蝠的鼻叶结构进行扫描，建立原始三维数字模型结构，并以单独和组合的形式剔除鼻叶的组成部分，利用数值模拟方法计算不同鼻叶结构的声场，通过对比不同鼻叶结构产生的近场声压幅度图和远场辐射波瓣图，研究埃及裂颜蝠鼻叶的各个组成部分在辐射波束形成过程中的作用。

1 埃及裂颜蝠

埃及裂颜蝠（Egyptian slit-faced bats，Nycteris thebaica）属于小蝙蝠亚目中的夜凹脸蝠科（Nycteridae），以脸中有一对裂缝而得名。除鼻叶特征明显外，埃及裂颜蝠具有大耳朵、小耳屏，两耳在基部相连，其尾巴的末端有一个T字形的尾骨与尾膜相连。裂颜蝠食性杂，主要以无脊椎动物为主，尤其喜欢捕食蝎子，其栖息地点主要是山洞、树洞以及被遗弃的矿洞。埃及裂颜蝠在低于其声呐信号频率时，具有很强烈的接收方向性，而当蝙蝠使用自身的回声定位系统时，其接收方向性较低。由于埃及裂颜蝠经常盘旋在接近地面的低空或者树顶，其利用低强度宽带信号不仅能够克服由较短延时所引起的发射波和反射波产生的叠加影响，还可以通过减少背景回声的方式得到较高的目标分辨率。

埃及裂颜蝠的鼻叶结构（高度为12.3 mm）如图1所示，埃及裂颜蝠的鼻叶主要由3个部分组成：①凹坑（Pit）；②上叶（Upper leaf）；③下叶（Lower leaf）。凹坑是一个体积较大的深坑，位于鼻叶结构的顶部。凹坑与正下方的一条凹槽相连，该凹槽一直向下延伸到鼻孔，称之为裂缝（Slit）。上叶和下叶分布在裂缝的两边，其实质是一些突出的肉质组织。上叶是比较对称两部分，形状面积不大，而下叶则是完整的一部分，形状为“U”型，面积较大。数值研究表明，凹坑的作用相当于双重弯曲的声学反射器［8］。埃及裂颜蝠利用鼻叶能够形成含有复杂的多重谐波组合而成的调频（FM）生物声呐信号［9］。

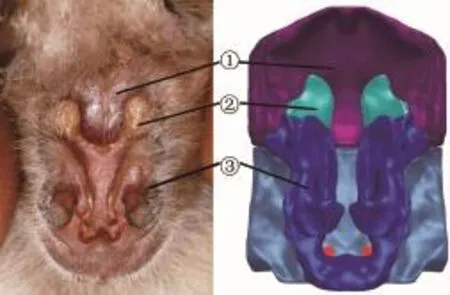
图1 埃及裂颜蝠的鼻叶结构图

2 数值研究方法

对于实际研究的声场问题，可以利用实验和理论分析计算相结合的研究方法。但是实际研究的声场问题往往较为复杂，而且通过实验获得声场数据的实现过程较复杂，结果也存在一定的误差和随机性，所以利用数值解得到声场传播计算结果不失为一种方便且精确的研究方法。随着计算机技术的发展和应用，声场研究中所使用的数值方法从20世纪50年代开始也得到了相应的发展。由于埃及裂颜蝠的超声辐射波束从近场传播到远场，因此传播声场的数值计算包括近场声场计算和远场声场计算。在研究过程中，利用时域有限差分法计算近场声场，而利用基尔霍夫积分得到远场声场的数值解。

2.1 时域有限差分法

1966年，Yee首次提出时域有限差分法FDTD（Finite different time domain method）［10］，并将该方法用于电磁场数值计算，随着计算机技术的高速发展，自20世纪80年代以来，时域有限差分法已经在电磁学和声学等领域得到广泛地发展［10－12］。FDTD方法之所以可以得到较为精确的计算结果，是因为这种方法在直接离散化处理波动方程的同时减少了不必要的假设。此外，FDTD方法还可以处理形状复杂、多种材料复合的结构，几乎可以对各种形状、各种材料的声学介质进行计算。FDTD方法通过计算声波在介质中的传播可以直观地给出声场随时间推进的演化过程，在计算机上以伪彩色方式显示，这种声场可视化结果清楚地显示了物理过程，便于对研究结构的声学功能的分析。另外，FDTD方法还可以配合傅里叶变换，通过一次计算可以得到在很宽频域内的计算结果，便于研究系统的频率特性。

FDTD计算区域如图2所示，在计算近场声场时，时域有限差分法需要将计算区域分为内部的常规计算区域和作为吸收边界条件的完全匹配层PML（Perfectlymatched layer）。内部区域是一个长方体，埃及裂颜蝠的鼻叶结构被包含在这个长方体空间内。完全匹配层区域满足吸收边界条件，具体来说，完全匹配层合理的参数设置可以保证在计算区域内，声波在内部常规区域与完全匹配层的界面上不会引起明显的反射。因为计算机的计算能力有限，过大的计算空间将占据计算机大量的内存并消耗大量的时间，因此需要设置完全匹配层，从而形成截断边界。截断边界的设置是一种吸收边界条件，吸收边界条件由最初简单的插值边界到Mur吸收边界发展到完全匹配层吸收边界，吸收效果逐渐变好，完全匹配层是由Berenger于1994年提出并应用于电磁场的数值分析［11］，随后科研人员又将这种方法引入到声场计算［13］。

图2 FDTD计算区域图

在对埃及裂颜蝠的鼻叶结构进行计算之前，计算区域需要网格化处理。网格由有限差分的立方体单元网格组成，立方体单元的顶点就是有限差分的节点，立方体体素的边长等于有限差分的节点间距。有限差分网格元胞如图3所示，图中p、ux、uy、uz表示物理量的位置，i、j、k分别表示x、y、z方向上的空间位置。

图3 Yee声学网格元胞图

利用时域有限差分法对近场声场计算的时候，三维数字结构需要添加激励源。对于埃及裂颜蝠鼻叶结构来讲，在两个鼻孔的出口表面添加两个完全相同的高斯脉冲点源［14］，频率范围61～97 kHz，频率间隔为0.5 kHz。在进行数值计算时，声源随时间的变化由式（1）表示为

式中：p为瞬时声压，kg／m2；t0是时间偏移值，s，其作用是使脉冲激励在起始时刻具有较小的值和平滑的上升曲线；τ为高斯脉冲宽度，s，它是由计算时的声信号的最高频率fmax决定，fmax的数值是100 kHz；τ的表达式由式（2）表示为

声波在介质内传播时，满足的连续性方程和欧拉方程分别由式（3）和（4）表示为

埃及裂颜蝠鼻叶结构的三维数字模型与长方体计算空间表面之间的介质是空气，因此三维数字结构的表面对于超声波来说是硬边界。所以，声波会在鼻叶结构和空气之间产生全反射，此现象的边界条件由式（6）表示为

由于计算空间是一个长方体，在三维直角坐标系中，整个计算空间（包括内部的常规区域和PML）是由Yee氏网格元胞组成，这些元胞的边长与三维数字结构的立方体体素边长相同，根据Yee提出的差分计算方法，首先在空间建立矩形差分网格。

在FDTD计算中，确保该算法有意义的前提是保证离散差分方程组的解是收敛和稳定的。收敛性是指当空间离散间隔趋于零时，在任意时刻差分方程组的解在空间任一点都趋于原方程组的解，稳定性是指采用的离散间隔能保证差分方程组的数值解与原方程的严格解之间的差为有界。如果不能保证数值解的收敛和稳定，那么这种不稳定性会随着时间步的推移而增加。在三维计算空间下，计算时所需的时间步长应满足的Courant稳定条件［15］由式（7）表示为

采用式（7）的稳定性条件可以保证时间步长计算的稳定性。由于计算采用的Yee元胞为立方体，长度Δx＝Δy＝Δz＝Δh＝90μm，所以Courant稳定条件由式（8）表示为

2.2 基尔霍夫积分

利用傅里叶变换，将近场FDTD有限区域的瞬时声压变换成复声压振幅［13］，利用基尔霍夫积分对有限区域外的任一点r→处声压的振幅P（r→）进行计算。基尔霍夫积分公式由式（9）表示为

根据基尔霍夫积分公式，可以得到球面点代表的声场远场的数值解。这个球面上的取值点在方位角方向（θ）和仰角方向（φ）的间隔均为1°。将这些点的幅值进行归一化，也就是所有方向上（θ，φ）的幅值除以幅值的最大值，归一化后的幅值D（θ，φ，f）为实数且0≤D（θ，φ，f）≤1，对于给定的声音频率f均能求出对应的远场数值解。

远场声波振幅的三维等值面图形象地展现了不同频率下的不同鼻叶模型的辐射波瓣图。在球坐标系中，远场声压幅度公式由式（10）表示为

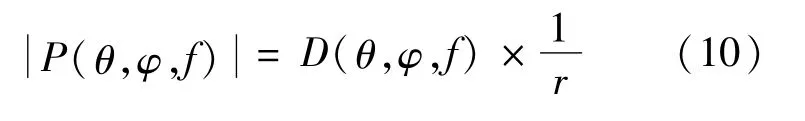
式中：D表示方向性；r表示球半径，m；远场声压幅度可以看作是D和的乘积［16］。对于方程中给定的远场幅度的表面，声源到等幅度面的球半径r与该方向的方向性D成正比。对于不同鼻叶结构形成的辐射波瓣图，它们形状之间的相似性可以用归一化的相关系数ρ1，2（f）表示。ρ1，2（f）由式（11）表示为

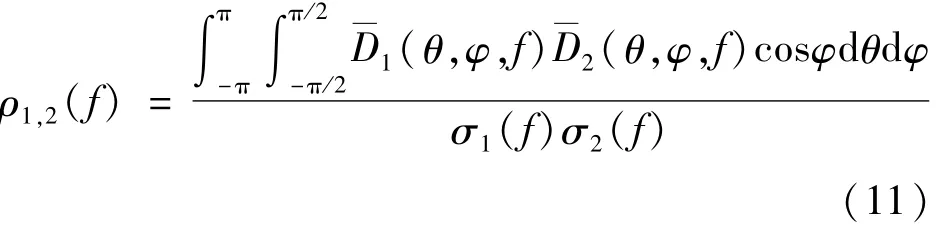
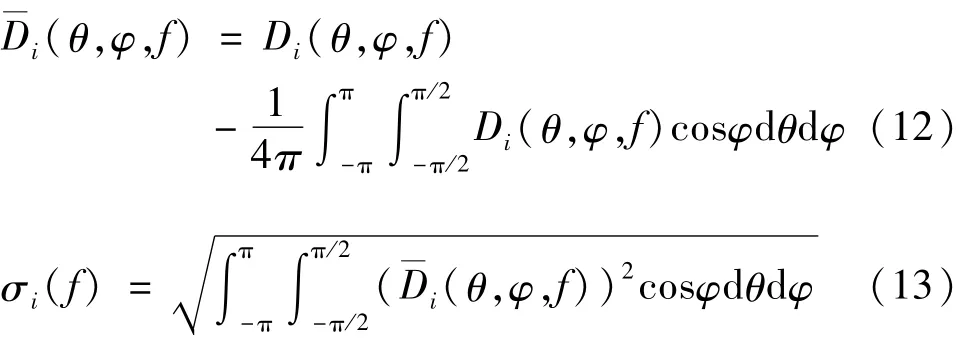
3 数值模型的建立

3.1 样本的获取

根据蝙蝠的习性特点选择捕捉方法，例如在湖边搭建雾网，在树林里搭建陷阱，或者在山洞内用手抄网捕捉蝙蝠。蝙蝠通常有冬眠的习惯，其冬眠会选择在洞穴当中，因此捕捉冬眠状态的蝙蝠较为容易。根据埃及裂颜蝠的特征确定样本种类后，将其放进专门的收纳袋中，记录捕获蝙蝠的时间及地点，并带回实验室做进一步测量，包括称重、测量翼展和前肢等。另外，需要对各个蝙蝠样本进行拍照存档，尤其是声呐器官，以便与后期的CT扫描图像进行参照对比。在录制蝙蝠声呐信号的过程中，为了记录下不同蝙蝠在飞行状态和静止状态下的超声信号，需要利用超声波探测器在无噪声的情况下多次录制并保存。所有测量记录工作结束后，将扫描用到的蝙蝠样本浸泡在酒精溶液中，以便在扫描工作中作进一步处理，其它多余的蝙蝠样本可以放归自然，或者饲养在专门的实验室内。

3.2 模型的建立

首先利用微型X射线断层扫描仪对埃及裂颜蝠的鼻叶结构进行扫描，利用三维锥形光束重建算法对投影图进行处理，得到相应地一组断层图像。但这些断层图像中含毛刺和噪声，不能直接生成用于声场计算的三维数字结构，因此需要对断层图像进行高斯平滑和二值化处理［4，8］。高斯平滑是利用高斯滤波器消除断层图中的毛刺和噪声，得到灰度变化平缓的图像。二值化处理则是选择一个合适的阈值将图像处理成只包含两种灰度等级（黑色和白色）的二值化图像，其中黑色表示埃及裂颜蝠的鼻叶结构，白色表示周围空气。最终利用VTK（可视化工具包）对二值化图像进行三维重构，得到了由立方体体素（边长90μm）构成的埃及裂颜蝠的鼻叶结构的三维数字模型。

通过删减体素的方式对鼻叶各部分进行剔除，以单独剔除或组合剔除的方式得到新的鼻叶结构。每个模型都由3个大写字母表示，每一个字母分别代表鼻叶结构的一个部分，“P”代表凹坑（Pit）、“U”代表上叶（Upper leaf）、“L”则代表下叶（Lower leaf），加括号的字母表示被剔除的部分，例如“PU（L）”表示的是保留凹坑和上叶而去掉下叶的鼻叶结构，以此类推。

利用计算机对各个鼻叶模型进行模拟计算，通过与完整鼻叶结构形成的近场声压幅度和远场辐射波瓣图进行对比，研究埃及裂颜蝠鼻叶结构的3个部分（凹坑、上叶和下叶）对辐射声场的影响。

4 数值计算结果分析

4.1 近场声压幅度

对于完整的埃及裂颜蝠鼻叶结构PUL，其近场声压振幅较大的区域主要位于鼻孔前方，声波在凹坑的前方区域会明显地发生反射现象，该区域的声压幅度也比较大。对于去掉凹坑的鼻叶结构（P）UL，该模型鼻叶前方的声压幅度明显减小，原凹坑结构前方的区域没有声波反射现象，而鼻叶前方周围区域的声压幅度变化不大。与完整的鼻叶结构相比较，去掉上叶结构的模型P（U）L的凹坑附近的声压幅度有所增强，而凹坑前方的声压幅度则有轻微得下降。对于去掉下叶的鼻叶结构PU（L），其近场声压幅度的分布在整体上有明显得下降。埃及裂颜蝠不同鼻叶结构的近场声压振幅分布如图4所示。

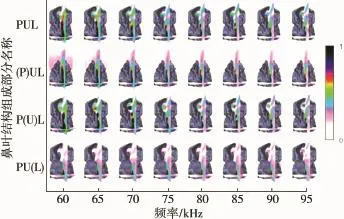
图4 埃及裂颜蝠不同鼻叶结构的近场声压振幅分布图

4.2 远场辐射波瓣图

对于实验中所给定的频率范围，完整鼻叶结构的辐射波瓣图中都含有一个明显的主波瓣，当频率发生改变时，主瓣会分裂成副瓣，同时旁瓣的数量也会改变。埃及裂颜蝠不同鼻叶结构的远场辐射波瓣图如图5所示。

图5中，当信号频率大于65 kHz时，波瓣的方向性有所增强，原始的主瓣会分裂成两个副瓣，周围的旁瓣数量也会增加。与完整鼻叶结构相比较，剔除凹坑的鼻叶结构（P）UL始终只有一个主波瓣，并且主瓣波束范围变大，随着频率的增加，主瓣方向向上偏移，旁瓣数量增加。无上叶结构P（U）L的变化趋势与完整鼻叶结构相类似，主瓣变化不大，只是旁瓣的幅度有所减小。无下叶结构PU（L）在频率低于80 kHz时的变化与完整结构类似，在频率高于80 kHz时，幅度较大的副瓣方向向上，旁瓣的幅度比较均匀。

图5 埃及裂颜蝠不同鼻叶结构的远场辐射波瓣图

对于同时剔除掉凹坑和上叶结构（P）（U）L，其主瓣范围随着频率的增加而增大。同时去掉凹坑和下叶的结构（P）U（L）的变化和只去掉凹坑的结构（P）UL的变化相类似，但是（P）U（L）结构的旁瓣幅度相对较小。而剔除上叶和下叶的结构P（U）（L）的变化趋势和只去掉下叶的结构PU（L）相似。当把三个部分全部剔除掉时，得到的（P）（U）（L）结构的辐射波瓣图有且仅有一个主瓣，与完整结构相比，主瓣波束范围变大，旁瓣的数量减少并且幅值降低。

从图5中可以看出，对于剔除掉不同结构的鼻叶，其辐射波瓣图有明显的差异。剔除凹坑使得主瓣不能分裂成两个副瓣，影响主瓣的波束宽度，同时也会影响旁瓣形成。而单独或同时除去上叶和下叶不仅会影响主瓣的指向性，也会影响旁瓣的宽度和指向性。同时剔除凹坑和上叶的结构对辐射波瓣图的影响比单独剔除掉两者中任一部分所产生的影响更明显，其辐射波瓣图中的主瓣在变大的同时旁瓣会变小。同时剔除三部分的结构只是随着频率的增加主瓣波束宽度变小，但主瓣波束宽度普遍比完整结构的宽。

4.3 辐射波瓣图的相关性系数

为了明确鼻叶的不同结构对辐射波瓣图的影响，利用归一化相关性系数对完整鼻叶结构和不完整鼻叶结构的辐射波瓣图的指向性进行了对比，如图6所示。去掉凹坑的鼻叶结构（P）UL的相关性系数在低于75 kHz时，随着频率的升高而降低，在高于75 kHz时，随着频率的升高而增加，即在75 kHz时，该结构的相关性系数最小，对远场声场的影响最大。无上叶的鼻叶结构P（U）L的相关性系数几乎接近1，并且随频率变化不大，即无上叶的鼻叶结构对远场声场的影响最小。对于去掉下叶的鼻叶结构PU（L），其波瓣图的相关性系数会随着频率的变化而不同，在实验所给定的频率范围内，60 kHz时的相关性系数最大，95 kHz时的相关性系数最小，相关性系数的大体变化趋势是随着频率的增加而减小。去掉凹坑和上叶的结构（P）（U）L的相关性系数与只去掉凹坑的结构（P）UL的相类似，而去掉凹坑和下页的结构（P）UL、去掉上叶和下叶的结构P（U）（L）和三部分同时被去掉的结构（P）（U）（L）的相关性系数与PU（L）结构的相似，大体趋势都是随着频率的增加而减小，但整体的相关性系数会明显降低。

图6 各鼻叶结构的辐射波瓣图的相关性系数图

5 结论

通过上述研究表明：

（1）凹坑通过向前反射声波对近场声场进行聚焦，从而影响远场辐射的方向性。在相关性系数图中，无凹坑结构在75 kHz时的相关性系数最低，表现出明显的频率选择性，说明凹坑结构可以提高蝙蝠在某个频率段的探测能力。

（2）上叶主要调节凹坑周围的声压幅度和主瓣、旁瓣的相对幅度，无上叶结构P（U）L的相关性系数接近1，说明上叶对声场的影响作用不明显。下叶则对近场声场的幅度和远场的主瓣波束聚焦起重要作用。

（3）同时去掉多个部分的鼻叶结构对声场的影响作用更为明显且复杂，比如去掉凹坑和上叶的结构（P）（U）L比单独去掉两部分的结构对声场方向性的影响明显，结果会造成主瓣变大而旁瓣变小，并且去掉两个部分的模型的相关性系数大都小于0.9。而三个部分全被剔除掉的鼻叶结构（P）（U）（L）对声场的分布产生的影响最大，其相关性系数平均值低于0.85。

埃及裂颜蝠在发射超声波的过程中，鼻叶结构会产生反复张合的现象。因此，埃及裂颜蝠鼻叶对辐射波束形成的影响作用可能与此现象存在联系，即埃及裂颜蝠通过调节鼻叶结构的形状来影响辐射声场的形成，从而对不同的生存环境进行探测。

［1］ Zhuang Q.，Müller R..Noseleaf furrows in a horseshoe bat act as resonance cavities shaping the biosonar beam［J］.Physical Review Letter，2006，97：21870101－21870104.

［2］ Feng L.，Gao L.，Lu H.W.，et al..Noseleaf dynamics during pulse emission in horseshoe bat［J］.PLOSONE，2012，7（5）：1－6.

［3］ He W.K.，Pedersen S.C.，Gupta A.K.，et al..Lancet dynamics in greater horseshoe bats，Rhinolophus ferrumequinum［J］.PLOSONE，2015，10（4）：1－13.

［4］ Kobayasi K.I.，Hiryu S.，Shimozawa R.，etal..Vocalization of echolocation-like pulses for interindividual interaction in horseshoe bats（Rhinolophus ferrumequinum）［J］.Journal of the Acoustic Society of America，2012，132（5）：417－422.

［5］ Gupta A.K.，Müller R..Effects of the source location on numerical biosonar beampattern predictions for bat noseleaves［C］.Montreal：Proceedings of Meetings on Acoustics，2013.

［6］ Matsuta N.，Hiryu S.，Fujioka E.，et al..Adaptive beamwidth control of echolocation sounds by cf－fm bats，Rhinolophus ferrumequinum nippon，during prey-capture flight［J］.Journal of Experimental Biology，2013，216：1210－1218.

［7］ Mantani S.，Hiryu S.，Fujioka E.，et al..Echolocation behavior of the Japanese horseshoe bat in pursuit of fluttering prey［J］.Journal of Comparative Physiology A，2012，198（10）：741－751.

［8］ Zhuang Q.，Wang X.M.，LiM.X.，et al..Noseleaf pit in Egyptian slit-faced bat as adoubly curved reflector［J］.Europhys Letter，2012，97（4）：4400101－4400106.

［9］ Gray P.A.，Fenton M.B.，Cakenberghe V.V..Nycteris thebaica［J］.Mammalian Species，1999，612：1－8.

［10］Yee K.S..Numerical solution of initial boundary value problems involving Maxwell equations in isotropic media［J］.IEEE Transaction on Antennas and Propagation，1966，14（3）：302－307.

［11］Berenger J.P..A perfectly matched layer for the absorption of electromagnetic waves［J］.Journal of Computational Physics，1994，114：185－200.

［12］李太宝.计算声学［M］.北京：科学出版社，2005.

［13］Sullivan D.M..Electromagnetic Simulation Using the FDTD Method［M］.New York：Institute of Electrical and Electronics Engineers Press，2013.

［14］Fenton M.B.，Bell G.P..Recognition of species of insectivorous bats by their echolocation calls［J］.Journal of Mammalogy，1981，62（2）：233-243.

［15］Ta？ove A，Brodwin M.E..Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell’s equations［J］.IEEE Transaction on Microwave Theory and Techniques，1975，23（8）：623－630.

［16］Urick R.J..Principles of Underwater Sound［M］.New York：McGraw－Hill，1983.

Numerical study of structure of em ission beam form ing in Egyptian slit-faced bat

Zhuang Qiao，Chen Xiaoqian，Zhang Meisheng
（School of Science，Shandong Jianzhu University，Jinan 250101，China）

Smart antenna is the indispensable key technology of the third generation mobile communication system，and theoretical basis obtained by this work can improve the characterise of smart antenna.The purpose of this study is to explore the effect of different parts（pit，upper leaf and lower leaf）of noseleaf on ultrasonic emission beamforming using finite difference time domainmethod（FDTD）and Kirchhoff integral.Three dimensional numericalmodel of noesleafwas built by scanning sample and processing scanned images，and all various models of noesleaf were got by removing different sections separately or together.Then，all models were studied by numerical method. Acoustic near-field pressuremagnitude，far-field radiation pattern and directivity correlation coefficient were represented as results.Simulation results show that the pit has a significant impact on increasing magnitudes near the area of pit，and it also can focus the acoustic near field as well as shaping the radiation patterns and hence enhancing the directionality.In terms of the function of upper leaf，it can adjust the amplitudes of the acoustic beam near the pit and front.The lower leaf seems to overall focus the acoustical near field.What’smore，interactions between the acousticeffects of the partswere also evident，and different combinations of three parts generate complicated influence on beam-forming. Theaveragedirectivity correlation coefficientof amodelwhich was removed all three parts is lower than 0.85，this phenomenon indicates that this kind ofmodel has themostobvious effecton the distribution of sound field.

Q62

：A

1673－7644（2017）02－0118－07

2017－02－05

国家自然科学基金项目（11374193）；山东建筑大学博士科研基金项目（XNBS1276，XNBS1269）

庄桥（1970－），男，副教授，博士，主要从事仿生声学等方面的研究.E-mail：zhuangqiao＠sdjzu.edu.cn