椭圆形切扇修形对波瓣混合器掺混性能影响
赵 彤,黄沛霖,姬金祖
(北京航空航天大学 航空科学与工程学院,北京 100000)
航空宇航工程
椭圆形切扇修形对波瓣混合器掺混性能影响
赵 彤,黄沛霖,姬金祖
(北京航空航天大学 航空科学与工程学院,北京 100000)
在保证面积不变的情况下,选取不同的长轴、短轴,对波瓣混合器进行椭圆形切扇修形,研究切口深度与宽度对波瓣混合器掺混性能的影响规律。使用商用CFD软件对流场进行数值模拟。结果显示,对波瓣侧壁进行切扇处理会加强流向涡的强度,切扇越深,流向涡强度越大;切扇波瓣流向涡的耗散速率要大于基准波瓣混合器的流向涡耗散速率,预示着更为高效的掺混;引射系数与切口深度成正比,而总压恢复系数与切口深度成反比。考察了两种衡量热混合效率的模型并对其信度进行了比较,发现在x=0.4 m之前切扇可以提高热混合效率,而在x=0.4 m之后,基准波瓣混合器热混合效率要大于切扇波瓣混合器。
波瓣混合器;切扇修形;流向涡;引射系数;总压恢复系数;热混合效率
波瓣混合器具有出色的掺混性能,有增加推力、抑制尾焰红外特征信号和降低噪声等功能,因此被广泛的应用于发动机的排气系统。国内外许多专家、学者对波瓣混合器管进行了大量的实验研究与数值模拟研究。这些研究揭示了波瓣加强掺混的机理,同时在工程上为波瓣设计提供了依据。波瓣混合器增强射流掺混的主要影响因素可以总结为[1]:(1)波瓣特殊外形诱导生成的大尺度流向涡;(2)褶皱的出口增加了主流与次流的接触面积;(3)尾迹剪切层Kelvin-Helmholtz失稳发展出来的正交涡。Skebe指出波瓣扩张角的增大有利于增强流向涡,加速掺混[2]。但是扩张过大会造成大量低能流体在波谷堆积,进而导致流动分离。对波瓣进行切扇处理可以减少波瓣扩张角过大带来的负面影响[3]。早在NASA的E3项目研究人员就已经对切扇波瓣的性能进行了研究[4-5]。Yu等[3,6]通过实验系统地研究了切扇对波瓣性能的影响,指出切口处可以形成附加的涡结构,产生更大的流向环量,同时流向环量的衰减速度也更快,从而具有更好的掺混性能。刘友宏等[7-9]则是以实际工程应用为背景,使用数值模拟,通过分析射流热掺混效率、总压损失等评价不同程度的切扇修形对射流掺混的影响。
尽管上述文献对波瓣切扇进行了细致的研究,但是这些文章中所使用的切扇形状并不相同,如文献[6]只针对一种三角切扇形状进行了研究;文献[7]虽然研究了不同椭圆切扇形状,但只是使用“切扇程度”笼统地对其进行了描述,而没有对切扇面积,切口深度、宽度对波瓣性能的影响作进一步的深入研究。本文通过对波瓣侧壁进行椭圆切扇处理,以引射系数、总压恢复系数、热混合效率等为评价指标,在切扇面积一定的条件下,对切口深度、宽度两种因素对波瓣性能的综合影响进行了研究。
1 数值研究方法
1.1 计算模型
图1为波瓣混合器示意图,混合管的直径为700 mm,长度为1 150 mm,波瓣混合器总长为600 mm,其中非波瓣区长度为265.5 mm,波瓣的具体尺寸见表1。

图1 波瓣混合器示意图

表1 波瓣几何参数
在切扇面积一定的情况下,选取一组具有不同长、短轴的椭圆对基准波瓣混合器侧壁进行切扇,用以研究切扇深度、宽度对波瓣掺混性能的影响。以基准波瓣混合器侧壁尾缘的中点为椭圆的圆心,侧壁尾缘为椭圆的一个轴对波瓣进行半椭圆形切扇。切扇面积保持900 mm2不变,更改椭圆的长轴、短轴组合,得到分别为90-20,60-30,45-40,33-55不同的切扇组合,其中第一个长度代表切口的深度,第二个代表切口的宽度(为了表示方便省略单位mm,下文同,同时对长度33进行了圆整),选取90-20情况作为示意,见图2。

图2 波瓣切扇修形示意图
1.2 计算网格
波瓣混合器的外形具有周期性,因此选择一个完成的波瓣结构进行计算,见图3。波瓣混合器的几何结构复杂,采用非结构网格,为了减少网格数量,对流动的核心区域进行网格加密。同时,为了提高求解精度,对波瓣喷管、中心锥、混合管等壁面采用三层棱柱网格进行加密,计算域的网格数量为300万+。
1.3 计算方法
使用FLUENT软件,模拟涡轴发动机试车台工况。波瓣混合器入口采用速度入口边界条件,其值为125 m/s,温度900 K;外界远场分别设为压力入口边界和压力出口边界,标准海平面条件。波瓣喷管、中心锥、混合管等壁面均采用绝热固壁边界条件。计算域两侧面设为对称边界。由于流动速度较低,气流设为不可压缩理想流体(Incompressible ideal flow)。湍流模式选择SSTk-ω模型。采用压力基隐式求解器,速度和压力的耦合采用SIMPLE算法,各项的离散格式采用二阶迎风格式。截取混合管内若干截面,以截面上的流场物理量作为计算收敛判定标准。

图3 计算域示意图
1.4 计算方法验证
为了验证所采用的计算方法的有效性及计算结果的可信性,本文对Hu[10,11]文章中的6瓣角波瓣实验进行了数值模拟,详见参考文献[12]。数值模拟结果与实验结果的对比如图4所示。通过对比可知,无论是速度矢量还是速度分布规律都与实验结果相符,尤其核心区速度大小和范围都与实验结果较一致,说明本文所用数值模型具有一定的精确性,计算结果可信。

图4 实验结果与计算结果对比图
2 结果与分析
2.1 流场分析
图5给出了基准波瓣混合器在波峰对称切面上的流线-温度图,x轴的坐标原点固定在波瓣出口截面处。从图中可以清晰地看出波瓣混合器引射外界温度较低的次流到混合管中与高温气体的掺混。从流线可以看出,由于初始时次流的速度为零,从混合管入口(x=-0.1 m)到x=0.2 m处次流在混合管管壁附近出现分离。随着主次流掺混的进行,在波瓣外扩张角的作用下,高温气体在x=0.4 m附近触壁。其他切扇情况的流线-温度图均与基准波瓣相似,只不过由于切扇作用使得混合气流在波瓣侧壁附近的掺混要略快于基准波瓣,因此不再赘述。
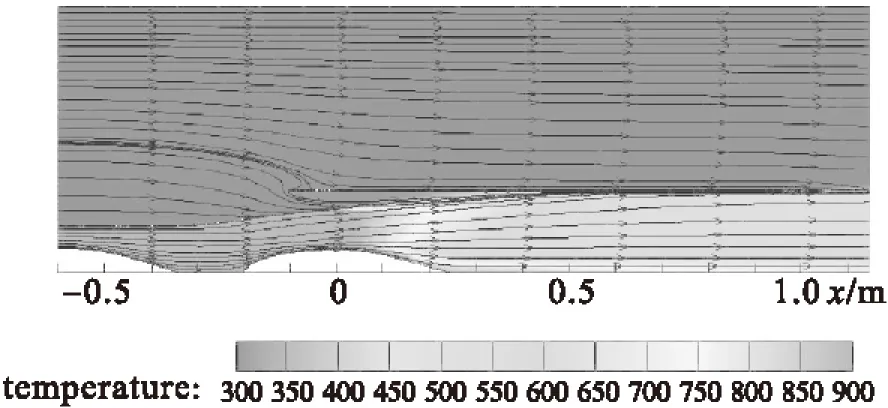
图5 波峰切面轴向流线-温度图
图6a、6b给出了基准波瓣混合器、90-20切扇波瓣混合器在波瓣出口附近相同截面上的横向速度矢量图。为了更清楚的揭示主流、次流的相对流动,矢量的颜色用温度区分。对切扇波瓣低温次流在主流引射作用下可以从切口流入主流,挤压高温主流,使得高温区变窄。这种引射作用也为流向涡的产生提供了额外的能量,同时由于切口的存在为主次流的相对转动提供了空间,因此90-20在波瓣侧壁附近已经明显地出现了流向涡涡核,而基准波瓣还只是主、次流的相对运动,流向涡的产生并不明显,见图6c、6d。通过以上分析可以预见切扇可以在出口处增加流向涡的强度。
2.2 流向涡
由波瓣特殊几何外形诱导所形成的流向涡,深刻地影响着波瓣的掺混性能,更强的流向涡与更快的耗散速率,意味着更高效的掺混[3]。引入流向涡无量纲平均涡量,比较不同切扇情况对流向涡的影响。无量纲平均流向量定义如下:

图6 横截面速度矢量图
(1)
式中,Dmix为混合管直径,uP为波瓣混合器入口处主流速度,v,w分别为掺混流体沿y,z方向速度。

图7 流向涡沿轴变化规律
图7给出了流向涡无量纲平均涡量沿轴向不同位置的横截面的变化规律。如图所示,流向涡的变化主要分为3个阶段。第一阶段为x=0到x=0.062 m,为流向涡的产生阶段,此时波瓣特殊构型诱导的两股速度相反的二次流在压力梯度的作用下形成流向涡。第二阶段为x=0.062 m到x=0.4 m。此阶段完成了由流向涡主导的射流掺混,随着掺混的进行流向涡强度迅速下降。第三阶段为x=0.4 m到混合管出口截面,在此阶段流向涡强度逐渐减弱。在图中还可以看出,在产生阶段,基准波瓣混合器的流向涡强度要小于经过切扇处理的混合器。通过横向比较,流向涡的强度总体上随切扇深度的增加而增加。但比较60-30与90-20两种情况发现,60-30情况产生的流向涡要强于90-20情况,这表明了60-30切扇波瓣混合器的掺混性能可能要优于90-20切扇波瓣混合器;在第二阶段,切扇波瓣混合器的流向涡耗散速率要明显高于基准波瓣混合器,这暗示着更高效的掺混。同时,受到流向涡耗散速率的影响,在第三阶段切扇波瓣混合器的流向涡强度要小于基准波瓣混合器,且切扇深度越深,较之基准波瓣流向涡强度越小。另一方面,高温流体在x=0.4 m处触壁,而触壁后的流场形态会发生很大的变化。因此,上述现象是由于流体触壁还是由于流向涡衰减,需要更进一步的研究。为更明确地表现上述现象,表2选取了3个阶段的若干典型截面上的流向涡无量纲平均涡量值作为参考。

表2 流向涡无量纲平均涡量
2.3 引射系数
引射系数定义[13]为:
Φ=mS/mP
(2)
式中,mS为次流质量流量,mP为主流质量流量。表3给出了不同切扇处理的波瓣混合器的引射系数。其中基准波瓣引射系数最小,而90-20切扇处理的引射系数最大,且引射系数呈现随着切扇深度的增加而增加的趋势。

表3 引射系数
2.4 总压恢复系数
文献[12]中总压恢复系数定义为:

(3)
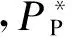

(4)
通过横向比较基准波瓣与不同切扇波瓣的总压恢复系数发现,前者在轴向各个截面均要大于后者,说明对波瓣进行切扇处理会降低波瓣混合器的总压恢复系数。另一方面,总压恢复系数随着切扇深度的增加而降低。图8给出各个波瓣混合器在x=0.3~1.0 m截面上的总压恢复系数,对于总压恢复系数呈现此种规律一种合理的解释是:当切扇深度越深,波瓣混合器引射的低能流体就越多,经过掺混后混合器气体的能量就越小,从而导致了主流更多的能量损失,因此总压恢复系数随切扇深度的增加而减少。另外,从流向涡的角度来看,更强的流向涡意味着更强的二次流动,而更强的二次流动必然会导致更大的总压损失。通过流向涡的变化规律可知,总体上切扇深度越深,流向涡越强,因此总压损失越大,总压恢复系数越小。综上所述,这两种原因的综合作用使得总压恢复系数呈现上述规律。

图8 总压恢复系数
2.5 热混合效率
本文首先使用刘友宏等[14]推导的热混合效率公式进行研究,公式定义为:

(5)
式中,Tp为喷管入口处主流温度,Ts为掺混前次流温度,Tm为掺混流体温度,TM为主、次流完全掺混后的温度,

(6)
图9a、9b给出了各个波瓣混合器沿轴向的热混合效率的变化趋势,通过观察可以发现,所有波瓣混合器的热混合效率都可分为两个阶段,第一阶段为x=0(即波瓣出口)到x=0.4 m,此时的热混合效率迅速增大,第二阶段为x=0.4 m之后,热混混合效率变化较为缓慢。在第一阶段所有研究的切扇波瓣的热混合效率均要大于基准波瓣,而在第二阶段切扇波瓣的热混合效率要小于基准波瓣的热混合效率且切扇深度越深,较基准波瓣的差值越大,参考文献[7]中的热混合效率变化趋势也给出了与本文相似的规律。另外通过对比场流向涡的变化,热混合效率的变化规律与流向涡的变化规律完全相似,这从另一个角度反映出流向涡对射流掺混的主导作用。x=0.4 m也成为了热混合效率变化的临界点。在x=0.4 m之前的各个截面上,横向比较不同切扇情况的热混合效率,热混合效率随切扇深度的增加而增加,但60-30的切扇情况的要优于90-20情况,如表4所示。

图9 热混合效率

表4 热混合效率
另外,本文采用了Tsui等[15]使用的混合度(mixedness)公式对波瓣的热混合效率进行了研究。热混合度公式定义如下:
(7)
其中,

(8)
(9)
σ0位于波瓣出口截面。通过计算发现,公式(7)预测的热混合效率趋势大致与公式(5)给出的规律一致,但值得注意的是,基准波瓣在出口附近的几个截面上的热混合效率均要大于切扇波瓣。然而,切扇使得主、次流在切口处便开始相互扩散混合,所以在波瓣出口附近切扇波瓣的热混合效率必然大于基准波瓣,这表明公式(7)给出的热混合效率并不可信。
为了解释上述错误的结果,进一步观察公式(7),注意到它的物理意义是,首先求出各个截面上温度混合的不均匀度σ,然后用出口截面的不均度对其进行归一化处理。然而对于不同的波瓣混合器出口处的不均匀度是不同的,在进行归一化处理时必然会抹平不同波瓣模型热混合效率的变化规律,甚至给出上述错误的结果。反过来,单独考察各个截面的温度混合不均度σ,认为其具有明确的物理含义可以直接表征热混合效率,1/σ越大表明掺混效果越好。通过1/σ对数据的研究发现,无论是纵向比较或是横向比较,其变化规律与公式(5)给出的热混效率变化规律完全一致,都预测了在60-30切扇形状附近可能存在针对热混合效率的最优切扇形状。以上分析一方面验证了本文数值求解具有良好的准确度,同时也说明了在考察不同波瓣热混合效率时,公式(5)可以有效地揭示规律,具有良好的信度。表5给出了沿x轴几个截面上的温度不均匀度作为参考。

表5 热混合效率与温度不均匀度
3 结论
通过对波瓣混合器侧壁进行切扇处理,使用数值模拟手段对流场进行分析,在本文的研究范围内得到如下主要结论:
(1)切扇处理可以增强流场中的流向涡,在出口附近切扇深度越深,流向涡增强的越多,但是在当切扇深度为60时流向涡要强于切扇深度为90的情况。在流向涡的耗散阶段,切扇波瓣混合器的耗散速率要快于基准波瓣混合器。在x=0.4 m之后,切扇波瓣混合器的流向涡强度要小于基准波瓣混合器。
(2)切扇处理可以提高波瓣的引射能力,且引射系数与切扇深度成正比,但代价是需要付出较大的总压损失。
(3)热混合效率的变化规律与流向涡的变化规律相似。在x=0.4 m之前,切扇波瓣混合器的热混合效率要大于基准波瓣混合器,而在x=0.4 m后切扇波瓣混合器的热混合效率要小于基准波瓣混合器。另外,在60-30切扇情况附近存在最优切扇情况,进一步优化设计已经进行。
(4)x=0.4 m成为波瓣混合器性能变化的临界点的原因可能与流向涡耗散和(或)流动触壁有关,需要进一步研究。
(5)通过比较两种不同的热混合效率评价模型表面揭示了公式5在评价热混合效率的准确性与有效性。
[1]Mengle V G,Dalton W N.Lobed mixer design for noise suppression:acoustic and aerodynamic test data analysis[R].NASA,CR-2002-210823:VOLL
[2]Skebe S A,Paterson R W,Barber T J R L.Experimental investigation of three-dimensional forced mixer lobe flow fields[J].AIAA,1988:3785.
[3]Simon C M Yu,T H Yip,C Y Liu.Mixing characteristics of forced mixers with scalloped lobes[J].Journal of Propulsion and Power,1997,13(2):305-311.
[4]Kozlowski H,Kraft G.Experimental evaluation of exhaust mixers for an energy efficient engine[M].1980:12.
[5]Kuchar A P,Chamberlin R.Scale model performance test investigation of exhaust system mixers for an energy efficient engine (E3) propulsion system[J].AIAA,1980(80):229.
[6]Mao R,Yu S C M,Zhou T,et al.On the vortices characteristics of lobe-forced mixer at different configurations[J].Experiments in fluids,2009,46(6):1049-1066.
[7]刘友宏,杜力伟,谢翌,等.波瓣凹扇修形对波瓣强迫混合排气系统性能影响[J].科学技术与工程,2013 (18):5226-5233.
[8]刘友宏,谢翌,郭楠.尾缘凹扇及综合修形对波瓣混合器性能影响[J].航空动力学报,2010 (2):243-250.
[9]丁玉林,刘友宏,谢翌,等.尾缘锯齿修形对波瓣强迫混合排气系统性能影响[J].航空动力学报,2012,27(10):2236-2242.
[10]Hu H,Saga T,Kobayashi T,et al.Dual-plane stereoscopic particle image velocimetry:system set-up and its application on a lobed jet mixing flow[J].Experiments in Fluids,2001,31(3):277-293.
[11]Cooper N J,Merati P,Hu H.Numerical simulation of the vertical structures in a lobed jet mixing flow[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit,Reno:Nevada,2005.AIAA- 2005-0635.
[12]盛志强,黄沛霖,姬金祖,等.改型对剑形深波谷交变波瓣喷管射流掺混的作用[J].北航学报,2014,40(10):1417-1423.
[13]李立国,靖周.航空用引射混合器[M].北京:国防工业出版社,2007:1-5.
[14]Xie Y,Liu Y H.A modified thermal mixing efficiency and its application to lobed mixer nozzle for aero-engines[J].Heat Transfer Research,2011,42(4):317-335.
[15]Tsui Y Y,Wu P W.Investigation of the mixing flow structure in multilobe mixers[J].AIAA,1996,34(7):1386-1391.
(责任编辑:宋丽萍 英文审校:刘敬钰)
Numericalinvestigationintheeffectofovalscallopingmodificationontheaerodynamicsperformanceoflobedmixers
ZHAO Tong,HUANG Pei-lin,JI Jin-zu
(School of Aeronautic Science and Engineering,Beihang University,Beijing 100000,China)
Oval scalloping modification on a lobed mixer was conducted.A set of semi-ellipsis of the same area but with different length of major and minor axes which represent the depth and width of scalloping respectively was adopted.The effect on aerodynamic performance of the lobed mixer was studied in this paper by CFD software in terms of streamwise vorticity,pumping factor,total pressure recovery coefficientand the thermal mixing efficiency.The results show that deeper scalloping attains strongerstreamwise vorticity.The dissipation of streamwise vorticity of the scalloped lobed mixers is faster than that of baseline lobed mixer.Pumping factor is directly proportional to the depth of the notch while total pressure has an inverse relationship with the depth.The fidelity of two different models for thermal mixing efficiency is evaluated.It is revealed by comparison thatscalloping enhances thermal mixing efficiency beforex=0.4 mm.After that the baseline lobed mixer has a larger value than the scalloped mixers investigated.
lobed mixer;scalloping;streamwise vorticity;pumping factor;total pressure recovery coefficient;thermal mixing efficiency
2014-08-13
总装备部预研资助项目(项目编号:×××)
赵彤(1989-),男,辽宁朝阳人,硕士研究生,主要研究方向:飞行器总体设计、飞行器隐身设计,E-mail:tonyplanedesigner@163.com; 黄沛霖(1975-),男,浙江诸暨人,副教授,主要研究方向:飞行器总体设计、飞行器隐身设计,E-mail:562325678@qq.com。
2095-1248(2014)05-0001-07
V231.3;V211.3
A
10.3969/j.issn.2095-1248.2014.05.001

