基于遥感数据的山西东部油松林蓄积量估测方法研究

刘治国,王弟,张红,张霄羽,韩建平，王云霞

(1.山西大学 黄土高原研究所,山西 太原 030006;2.山西省林业调查规划院,山西 太原 030012;3.山西大学 环境与资源学院,山西 太原 030006)

基于遥感数据的山西东部油松林蓄积量估测方法研究

刘治国1,王弟2*,张红3,张霄羽3,韩建平2，王云霞2

(1.山西大学 黄土高原研究所,山西 太原 030006;2.山西省林业调查规划院,山西 太原 030012;3.山西大学 环境与资源学院,山西 太原 030006)

为了探讨油松林遥感估测模型的精度和适用性,以山西省晋东土石山立地亚区的170个油松样地作为研究对象,获取研究区的SPOT影像和DEM(Digital Elevation Model,数字高程模型)数据,提取170个样地的遥感波段信息和地形信息,结合地面调查数据,分别采用多元逐步回归模型、偏最小二乘回归模型和神经网络模型,建立油松林蓄积量的遥感估测方法,并进行精度验证。结果表明:1)基于遥感影像和DEM影像估测油松林蓄积量是可行的,三种方法都取得了满意的结果;2)三种方法相比,神经网络模型对油松林蓄积量估算的精度为82.13%,多元逐步回归模型的精度为76.73%,偏最小二乘回归模型的精度为77.09%,神经网络模型的估测精度更高。

油松林；蓄积量;遥感估测;多元回归;偏最小二乘回归;BP神经网络

0 引言

森林蓄积量作为反映一个国家或地区森林资源总规模和总水平的基本指标之一,其消长动态变化是林业经济、社会效益的主要表征参数,因此准确估计森林的蓄积量,对衡量森林生态环境具有重要意义。传统的测定森林蓄积量方法包括材积表法、标准木法、干距法等[1]，这些方法调查周期长,人力财力消耗大且不能及时反映森林蓄积量的动态变化。随着“3S”(遥感技术、地理信息系统、全球定位系统)技术的发展,很多学者已将3S技术多方面应运于森林蓄积量的研究[2-4]。包盈智等利用TM(Thematic Mapper)数据使用多元回归分析对森林蓄积量进行了估测[5];袁凯先使用了TM资料,运用材积表法与多元回归法验证了这种方法的可行性[6];施鹏程则采用PLS(Partial Least Square,偏最小二乘法)对密云县森林蓄积进行遥感估测所得模型具有较强适应性[7];李崇贵利用“3S”技术与BP(Back Propagation)神经网络结合,同时使用地面数据进行蓄积估测,所得结果也满足调查精度要求[8]。

关于森林蓄积量的遥感定量估测研究主要集中在如何提高遥感估测蓄积量精确度，同时在具体的森林经营单元上选择与蓄积量相关性较好的自变量因子[9-12]。国内外在选择蓄积量估测因子中,常常将估测因子分为地面实测因子、遥感因子。纯粹采用地面实测因子建模精度高,但工作量大、难以推广到样地以外区域,纯粹采用遥感因子建模精度较低,不能准确模拟森林蓄积量。而将两者结合,可以大大减少野外工作量,提高估测精度,如Gemmell等[13]基于 TM数据,采用KNN方法研究了各波段、郁闭度、林分面积大小以及地形要素对定量估测森林蓄积量的影响度,结果显示,郁闭度和蓄积量的相关系数最大,远远大于地形要素对蓄积量的影响。本文以山西省东部土石山的优势树种油松(Pinustabuliformis)作为研究对象,将遥感影像数据与地面数据相结合,采用多元逐步回归模型,偏最小二乘回归模型及神经网络模型,对油松林蓄积量进行估测,并比较三种方法的估测精度。目的是:1)以SPOT多波段影像和DEM为数据源,选取合适的影像因子和地形因子,对样地内油松林蓄积量进行相关性分析和共线性分析;2)基于增强型BP神经网络算法、多元逐步回归与偏最小二乘法建立油松林蓄积量遥感估测模型,通过比对探索更有效的油松林蓄积量估测方法。

1 内容与方法

1.1 研究区概况

油松是山西省主要的针叶树种,分布广泛,遥感影像数据色彩和纹理明显、树冠整齐。山西省森林资源一类清查(2010年)中涉及的油松林样地有381个,其中晋东土石山立地亚区分布较多,主要涉及安泽、沁源、长子、长治、壶关、平顺、潞城、黎城、屯留、襄垣、沁县、武乡、陵川、高平、泽州、榆社、左权、和顺、昔阳、寿阳、平定、盂县等22个县市。该立地亚区主要气候特点是冬夏长、春秋短、四季分明;日照比较充足,昼夜温差较大;春季少雨多风,干旱时有发生;夏季炎热且降雨量集中,年降水量400～600 mm,年际变化大;秋天云高气爽,降温快;冬季干冷。立地亚区内的土壤类型多以褐土、栗褐土和山地草甸土为主;地带性植被以常绿针叶林为主,主要优势树种有华北落叶松(Larixprincipis-rupprechtii)、油松(Pinustabuliformis)、侧柏(Platycladusorientalis)等,阔叶树种多为辽东栎(Quercuswntaishanica)、刺槐(Robiniapseudoacacia)、杨树(Populusspp.)等。

研究区的遥感影像采用2010年由SPOT卫星高分辨率多波段扫描仪(HRV)获取的遥感影像,包括10 m分辨率的全色波段和20 m分辨率的多波段数据。影像成像时间从5月份到11月份不等。 将381个油松林样方所在经纬度样方与遥感影像对应,获得每一个样方所对应的影像,剔除影像中有云或影像不清晰的样本、剔除影像月份在5月、6月和11月的样本,剔除掉蓄积量过大和过小的样本。本研究所采用的油松样地数量为170个。通过对不同数据来源进行分类、整理,本文选取的170个油松林样地海拔750 m～1 940 m,地貌类型以中山为主;样地坡度在25度以下的占53.53%;样地内油松林主要分布在北与东北坡向;以中龄林与近熟林为主,各占总数的60.00%和32.35%;郁闭度多介于0.4-0.6、0.6-0.8。

1.2 数据来源

将影响油松林蓄积量的自变量因子分为遥感因子、地形因子和地面因子。其中油松林蓄积量的数据是通过一类清查得到;地形因子是根据研究区的170个油松林小班的DEM数据,得到海拔(Altitude)、坡度(Slope)、坡向(Slope aspect);地面因子包括龄组(Age group)、郁闭度(Crown density)，主要是根据样地调查得到的;遥感影像因子包括SPOT影像的4个波段值;植被指数因子包括根据遥感影像波段值计算得到的NDVI(归一化植被指数)、RVI(比值植被指数)。

遥感影像处理过程为:由SPOT卫星高分辨率多波段扫描仪(HRV)获取的遥感影像,包括10 m分辨率的全色波段和20 m分辨率的多波段数据。对多波段影像进行了几何校正、图像融合、拼接及辐射校正等预处理,使总误差小于1个像元。根据一类清查中涉及研究区内的170个油松林样地的经纬度坐标,提取样地所在的森林小班,将小班边界与SPOT影像(2010年)叠加,在ENVI中提取每个油松小班所在像素的波段灰度值B1、B2、B3和B4(NIR近红外光、RED红光、GREEN绿光和SWIR短波红外线),根据遥感影像波段值计算得到每个小班的NDVI、RVI,模型的自变量因子具体总结见表1,且植被指数的计算方法如下:

NDVI=[p(nir)-p(red)]/[p(nir)+p(red)] ，

(1)

RVI=p(nir)/p(red) ，

(2)

其中,p(nir)、p(red)分别指影像相应波段的灰度值。

表1 数据来源

1.3 研究方法

将油松小班的遥感因子、地形因子和地面因子作为自变量,油松林蓄积量作为因变量,分别采用多元逐步回归、偏最小二乘回归以及BP神经网络进行蓄积量拟合。建模分别在SPSS13.0、SIMCA-P、MATLAB R2011b中实现。

分别采用三种建模方法进行了油松林蓄积量的估测,为了比较三种方法的优劣,选择MAE(the mean absolute Error),RMSE(the root mean square error)、精度Pc作为衡量算法性能的指标,具体定义如下:

(3)

(4)

(5)

2 结果分析

2.1 基于多元逐步回归分析法的油松林蓄积量估算

对样地各自变量因子与因变量蓄积量进行相关性和自变量间共线性分析,结果见表2。由表2可知,RED、GREEN、SWIR、海拔、龄组、郁闭度这6个因子与蓄积量的相关性达到了显著性水平(P<0.05),而NIR、NDVI、RVI、坡度、坡向这5个因子与蓄积量的相关性没有达到显著性水平(P>0.05)。从方差膨胀因子来看,NIR、RED、NDVI与RVI的方差膨胀因子均大于10,表明各波段之间与通过波段值计算得到的植被指数之间存在多重相关性。

表2 因子与样地蓄积量的相关性分析和共线性分析

由于自变量间存在着显著的相关性,易使模型估计失真,因此采用逐步回归法可以找出引起多重共线性的解释变量,将它排除出去。对170个样地的油松林蓄积量与自变量进行多元逐步回归,并对模型精度进行评估,结果见表3。从表3可以看出,郁闭度为最先引入模型的变量,选出的最优模型其郁闭度、龄组及RED的偏相关系数依次为0.733、0.689及-0.212,决定系数R2为0.632,通过比较使用此模型获得的表达式为:公顷蓄积量=-57.817+104.888*郁闭度+24.254*龄组-0.214*RED。从表3中的标准化偏回归系数可以表示模型中自变量对因变量的贡献大小,可以看出贡献度大小依次为:郁闭度>龄组>RED。

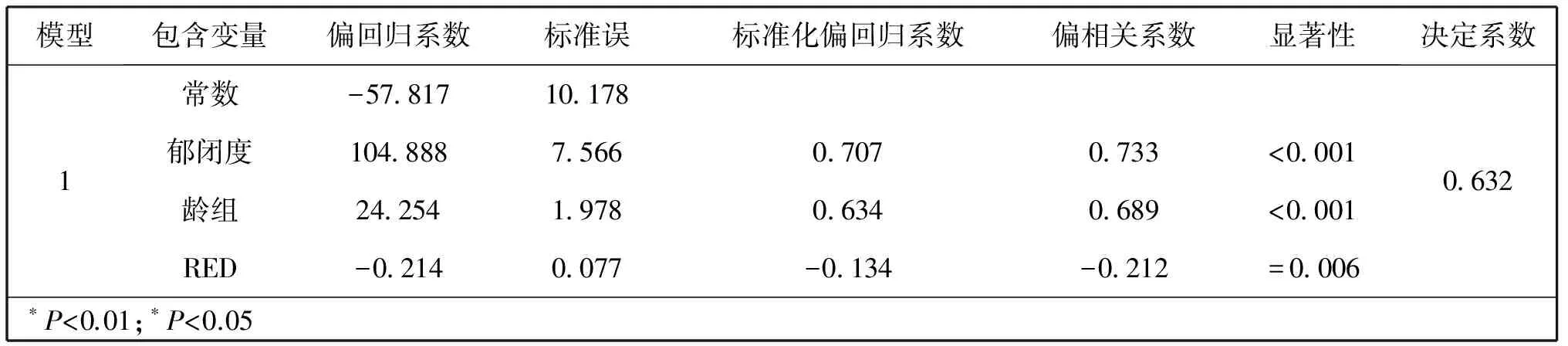
表3 油松林蓄积量估测的逐步回归模型

2.2 基于偏最小二乘法的油松林蓄积量估算

偏最小二乘回归可以解决自变量之间多重共线性问题。对170个样地的油松林蓄积量与自变量进行偏最小二乘回归分析。结果表明:在偏最小二乘回归计算过程中,共提取了3个主成分F1、F2、F3,这三个主成分一方面尽可能多地代表X中的变异信息,另一方面与Y相关联并能解释Y中的信息。F1、F2、F3对自变量X和因变量Y的解释能力分别为:38%,22%,3%,总解释能力为63%。

各自变量与蓄积量相关性结果见图1。由图1可知,自变量对蓄积量的解释度重要性依次为郁闭度>龄组>RED>GREEN>SWIR>NIR>海拔>RVI>NDVI>坡度>坡向,前三个变量的重要性与逐步回归中构建模型的3个自变量一致,这也说明两种模型对自变量的提取是一致的,也即郁闭度、龄组和RED对蓄积量估测起主要作用。偏最小二乘回归系数见表4,通过表4,构建蓄积量与11个自变量的偏最小二乘回归模型为:

蓄积量=-66.499-0.007×NIR-0.032×RED-0.165×SWIR+6.619×NDVI-0.079×RVI+0.007×海拔+0.057×坡度+21.463×龄组+104.963×郁闭度+1.333×坡向

Fig.1 Rank of factors图1 影响蓄积量的各因子重要性排序

2.3 基于BP神经网络模型的油松林蓄积量估算

神经网络模型的实质反映了输入输出之间的数学关系,这种数学关系由特定的网络结构确定,根据具体问题进行设计和训练。在170个样本中随机选取80%的样本(136个)作为训练数据,在Matlab中进行网络训练,通过不断调整训练参数,使预测误差达到最小,达到10-3后停止训练,总计训练3 000步,拟合完成后,将剩余的20%样本(34个)作为检验数据,代入训练好的模型中进行预测,并与实测值进行比较,进行精度检验。

表4 油松林蓄积量估测的偏最小二乘模型

构建的BP网络结构为10-3-1,即输入层有10个节点,隐藏层有3个tansig神经元,输出层有1个purelin神经元。模型的训练、验证和测试的相关分析见图2,可知模型训练样本的相关系数R为0.87,检验样本的R为0.76,测试样本的R为0.71,总体训练R为0.83。模型预测值与真实值以及模型预测误差见图3,可知预测值与实测值呈现一致的波动趋势,差异较小,预测的误差为-25～20 m3。这说明本文提出的方法在蓄积量估测的精度方面是可行的,并且随着样本量的增大,模型的精度会进一步提高[14-19]。

Fig.2 Artificial neural network model of stand volume图2 油松林蓄积量的神经网络模拟结果

Fig.3 Prediction value and error of artificial neural network model图3 模型预测值与真实值以及模型预测误差

2.4 三种方法拟合精度比较

对多元逐步回归、偏最小二乘回归以及人工神经网络三种建模方法进行精度比较,结果见图4和表5。由图4可以看出,神经网络模型的预测结果比偏最小二乘模型和逐步回归模型的预测结果更接近实际值。从表5可以看出,三种模型中,神经网络方法的检验精度最高、MAE和RMSE值最低。逐步回归模型和偏最小二乘模型的检验精度均低于神经网络模型,通过验证得到神经网络可以作为更优的蓄积量估测方法,同时也体现出这种方法具有更强大的泛化和预测能力。

Fig.4 Comparison of real value and estimation value of three models图4 实际值与理论值比较

估算方法检验精度MAERMSE多元逐步回归7673%12011456偏最小二乘回归7709%11951459人工神经网络8213%824977

由于森林蓄积量是受多因子影响的,而传统的多元线性回归模型和偏最小二乘回归模型是建立在线性假设的基础上的,因此预测的精度较低,在实际应用中受到很大限制。而基于非线性数量技术的人工神经网络模型,通过对输入输出数据进行训练和仿真,实现网络的自学习能力,能够较好地拟合预测研究在复杂情况下的非线性预测问题,比传统的线性回归模型有了很大的改进[20-21]。此外,本研究也有较高的实际应用价值,当进行其他地区或其他树种蓄积量估测建模时,可根据神经网络原理建立相应的神经网络模型进行估测。

3 结果与讨论

采用多元逐步回归、偏最小二乘法、神经网络分别建立对油松林蓄积量的估测模型,通过使用检验精度、MAE、RMSE对这三种方法的结果进行拟合精度比较。结果表明:1)利用BP神经网络对油松林进行蓄积量估算,最终模型的检验精度为82.13%,利用多元逐步回归和偏最小二乘回归分别对油松林进行蓄积量估算获得模型的检验精度分别为76.73%与77.09%。2)本研究结果表明利用神经网络模型对油松林蓄积量遥感估测精度更高,所获得的理论结果与森林清查获得的地面数据的结果相近,表明该方法能够真实反映一定树种蓄积量。

本研究中发现:1)影像的选择、时空分辨率、影像成像时间和质量对于森林蓄积量的估算有很大的影响,使得影像的波段灰度值与蓄积量的关系不一致,甚至呈现相反的关系。未来研究应用分辨率更高的遥感图像,实现精确定位,可以减少估测误差。2)蓄积量估测因子的选择对估测准确性和精确性有很大的影响,将地面易测因子与遥感因子结合,可以大大减少野外工作量,提高估测精度。本文选取了遥感因子和地面因子结合进行蓄积量建模,所得模型的精度为82.13%,其中对蓄积量影响较大的3个因子分别是郁闭度、龄组和RED,遥感影像因子的影响较小,这与本文所选择的影像精度有关。如果在未来能通过更高分辨率的遥感影像,估算出冠幅或株数因子,则模型的精度会更高。3)未来的研究方向应该是从植被生产力形成的生理过程出发,研究具有生理学、生态学意义的机理模型,再利用神经网络等机器学习算法进行高精度定量估测。本文的研究结果虽然只适用于山西油松林的蓄积量模拟,但提出的研究方法可以推广到其他树种进行森林蓄积量的估测,对于最大限度地减少外业工作量,将具有重要的理论研究价值和社会、经济效益,为今后的森林固碳估测及森林规划管理提供科学依据。

[1] 程武学,杨存建,周介铭,等.森林蓄积量遥感定量估测研究综述[J].安徽农业科学,2009,37(16):7746-7750.DOI:10.3969/j.issn.0517-6611.2009.16.171.

[2] Macomber S A,Woodcock C E.Mapping and Monitoring Conifer Mortality using Remote Sensing in the Lake Tahoe Basin[J].RemoteSensingofEnvironment,1994,50(3):255-266.

[3] Tomppo E,Nilsson M,Rosengren M,etal.Simultaneous use of Landsat-TM and IRS-1C WiFS Data in Estimating Large Area Tree Stem Volume and Aboveground Biomass[J].RemoteSensingofEnvironment,2002,82(1):156-171.

[4] 张彦林.基于3S技术的山东省森林蓄积量定量估测研究[D].北京林业大学,2008.

[5] 包盈智,袁凯先,赵宪文,等.森林二类调查中蓄积量遥感估测方法应用实例[J].林业科学研究,1996,9(3):234-238.

[6] 袁凯先,陈玉山,包盈智,等.森林蓄积量的遥感估测[J].林业资源管理,1996(3):13-17.

[7] 施鹏程,彭道黎.基于偏最小二乘回归密云森林蓄积量遥感估测[J].江西农业大学学报,2013,35(4):798-801.DOI:10.3969/j.issn.1000-2286.2013.04.023.

[8] 李崇贵.用非线性理论研究以“3S”为基础的森林蓄积定量估测[D].北京：中国林业科学研究院资源信息研究所,2001.

[9] 洪伟,吴承祯,何东进.基于人工神经网络的森林资源管理模型研究[J].自然资源学报,1998,13(1):69-72.DOI:10.3321/j.issn:1000-3037.1998.01.012.

[10] 刘志华,常禹,陈宏伟.基于遥感、地理信息系统和人工神经网络的呼中林区森林蓄积量估测[J].应用生态学报,2008,19(9):1891-1896.

[11] 王淑君,管东生.神经网络模型森林生物量遥感估测方法的研究[J].生态环境,2007,16(1):108-111.DOI:10.3969/j.issn.1674-5906.2007.01.020.

[12] 汪少华,张茂震,赵平安,等.基于TM影像、森林资源清查数据和人工神经网络的森林碳空间分布模拟[J].生态学报,2011,31(4):998-1008.

[13] Gemmell F M.Effects of Forest Cover,Terrain,and Scale on Timber Volume Estimation with Thematic Mapper Data in a Rocky Mountain Site[J].RemoteSensingofEnvironment,1995,51(2):291-305.DOI:10.1016/0034-4257(94)00056-S.

[14] 刘书剑.沽源县森林碳储量遥感动态监测[D].北京林业大学,2011.

[15] 洪奕丰,林辉,严恩萍,等.基于偏最小二乘法的平南县森林蓄积量估测模型研究[J].JournalofCentralSouthUniversityofForestry&Technology,2011,31(7):80-85.DOI:10.3969/j.issn.1673-923X.2011.07.018.

[16] 陈楚,关泽群,张鹏林,等.利用RS和GIS的森林蓄积量偏最小二乘估测研究[J].湖北林业科技,2004(4):25-28.DOI:10.3969/j.issn.1004-3020.2004.04.007.

[17] 杜晓明,蔡体久,琚存勇.采用偏最小二乘回归方法估测森林郁闭度[J].应用生态学报,2008,19(2):273-277.

[18] 罗批,郭继昌,李锵,等.基于偏最小二乘回归建模的探讨[J].天津大学学报:自然科学与工程技术版,2002,35(6):783-786.DOI:10.3969/j.issn.0493-2137.2002.06.026.

[19] 李圣娇,舒清态,徐云栋,等.基于偏最小二乘回归模型的高山松蓄积量遥感估测[J].江苏农业科学,2015(8):182-185.DOI:10.15889/j.issn.1002-1302.2015.08.060.

[20] 罗胜琪.BP算法的改进与性能分析[J].中国科技博览,2011(33):408-409.

[21] 琚存勇,蔡体久.用泛化改进的BP神经网络估测森林蓄积量[J].林业科学,2006,42(12):59-62.DOI:10.3321/j.issn:1001-7488.2006.12.010.

Estimation for the Forest Volume ofPinustabulaeformisForest Based on Remote Sensing Data in East Shanxi

LIU Zhiguo1,WANG Di2*,ZHANG Hong3,ZHANG Xiaoyu3,HAN Jianping2，WANG Yunxia2

(1.InstituteofLoessPlateau,ShanxiUniversity,Taiyuan030006,China;2.ShanxiInstituteofForestInventoryandPlanning,Taiyuan030012,China;3.CollegeofEnvironmentScienceandResources,ShanxiUniversity,Taiyuan030006,China)

In order to compare the precision and applicability of different estimation models forPinustabuliformisbiomass based on remote sensing data,remote sensing band and terrain information of 170 sample plots ofPinustabulaeformisforest in an earth-rock soil region of eastern Shanxi were extracted from SPOT and DEM images. Associated with the ground survey data, this study employed the BP neural network model, multiple stepwise regression approach and partial least squares method to estimate the biomass volume ofPinustabuliformis. The accuracies of the models obtained from these three methods were verified and compared. The results showed that:1) all three approaches could estimate the biomass volume ofPinustabuliformiswith high accuracies;2) the neural network model had the highest accuracy among three models (82.13%), followed by partial least squares model (77.09%) and the multiple stepwise regression model (76.73%).

Pinustabulaeformisforest;stand volume;remote sensing estimation;multiple stepwise regression;partial least squares regression; BP neural network

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.01.027

2016-08-22；

2016-11-14

国家自然科学基金青年科学基金项目(41401643)

刘治国(1990-)，男，山西忻州人，硕士研究生，主要研究方向为森林生态学。E-mail:272752172@qq.com

*通信作者：王弟(WANG Di),E-mail:Dw1964@126.com

S718.5

A

0253-2395(2017)01-0187-08