卡瓣分离后气动特性数值研究

郭佳肄，陈学义，胡晓磊，孙船斌

（1.安徽工业大学 工程实践与创新教育中心，安徽 马鞍山 243002；2.山东电力设备有限公司，山东 济南 250022；3.安徽工业大学 机械工程学院，安徽 马鞍山 243002）

科学技术

卡瓣分离后气动特性数值研究

郭佳肄1，陈学义2，胡晓磊3，孙船斌3

（1.安徽工业大学 工程实践与创新教育中心，安徽 马鞍山 243002；2.山东电力设备有限公司，山东 济南 250022；3.安徽工业大学 机械工程学院，安徽 马鞍山 243002）

为了研究穿甲弹卡瓣分离后的气动性能，采用计算流体力学方法结合k-ε二方程湍流模型，建立卡瓣分离后翻转过程数值模型，在与相关实验结果对比验证的基础上，研究了不同翻转角度下卡瓣的气动系数变化规律.结果表明：卡瓣的气动参数变化符合周期性变化规律；卡瓣的升力系数、阻力系数和力矩系数与翻转角度密切相关.研究结果为卡瓣结构设计和运动轨迹预测提供基础.

卡瓣；计算流体力学；气动特性；数值模拟

穿甲弹是由穿甲弹弹体和三瓣卡瓣组成，其具有初速度高和飞行时间短等特点.卡瓣随弹体弹出炮口后，产生一系列机械和气动效应[1,2].先前的研究主要是对卡瓣的分离过程中的流场进行了详细研究[3-5]，而对卡瓣的抛落轨迹研究较少.试验证明，卡瓣分离后，在风速的影响下，其运动轨迹不在符合抛物线规律.为了准确的预测卡瓣弹出炮口后的运动轨迹，首先需要获得卡瓣的气动参数变化规律，因此研究卡瓣的气动特性变化规律具有重要的工程意义.

本文采用计算流体动力学方法结合k-ε二方程湍流模型，建立卡瓣分离后的数值模型，在与相关文献实验数据对比验证的基础上，研究了卡瓣翻转过程中不同翻转角下气动系数变化规律.

1 数学方法和模型

采用三维Navier-Stokes方程建立卡瓣分离后的气动特性，其流动控制方程如下[6]：

质量守恒方程

动量守恒方程

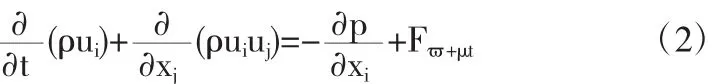
能量守恒方程

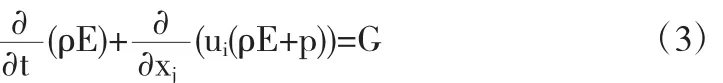
方程中ρ、u、p、E分别为空气的密度、速度矢量、压力和总能.

穿甲弹的物理模型如图1（a）所示，包括三瓣卡瓣和弹体，其中卡瓣的长度为30mm，由于三瓣卡瓣的气动特性具有类似，因此本文仅对其中一瓣进行研究，如图1（b）所示，图1（c）为计算区域网格模型，计算区域为卡瓣长度20倍的正方体区域，计算网格为120万网格左右.来流风速为7.9m/s.其中湍流模型采用k-ε二方程湍流模型[7].

图1 物理和数值模型

2 数值方法验证

为了验证建立数值方法的有效性，采用本文建立的数值模型研究S809翼型的升力系数变化规律，并与试验[8]进行对比.数值结果和试验结果对比如图2所示.由试验曲线和仿真曲线对比可以看出，采用本文数值仿真计算得到的S809翼型升力系数与试验结果误差在8%左右.这说明本文采用的数值模型是可靠的，可以用于分析卡瓣分离后的气动参数变化规律.

图2 S809翼型升力系数与实验对比曲线

3 结果分析

图3为在0°～360°的角度内，卡瓣分离后绕质心翻转过程时的压力云图（其中360°与0°相同），图4～图6为卡瓣分离后的升力系数、阻力系数和力矩系数在不同翻转角度下的变化曲线.翻转角度的定义为，卡瓣出筒时刻位置为0°，卡瓣低头时为正.

由图3（a）～（f）卡瓣的翻转过程云图可以看出，卡瓣脱离弹体翻转时，其迎风面受到风载荷的直接作用，导致其压力最大.而在背风面受回流的影响，其压力较小.

图4为卡瓣升力系数随翻转角度变化曲线，其中，卡瓣的升力系数定义为

式中，Fl为卡瓣的升力，ρ为空气密度，v为空气粘性，S卡瓣的投影面积.

从图4中的可以看出，在0°～360°范围内，卡瓣升力系数随翻转角度变化的曲线呈现先下降，再上升，然后再下降，又上升，最后下降的趋势.这是由于流场内卡瓣的插入，来流被分为上下两股，来流通过卡瓣后，又重新合成一股.由于卡瓣前后、上下不对称，因此升力系数呈现波动趋势，当迎角为120°和300°时，升力系数为最大值0.8.这是由于该角度情况下，卡瓣的升力与投影面积之比最大.当迎角为90°和270°时，升力系数为最小值-1.3.这是由于该角度情况下，虽然卡瓣的投影面积减小，但是升力减小的量级远大于投影面积减小的量级.从卡瓣的升力系数随翻转角度的变化曲线可以看出，在0°～360°范围内，卡瓣的升力系数以-0.25为中心，以1.05为振幅和180°为周期，进行周期性变化.

图5为卡瓣分离后阻力系数随卡瓣翻转角度变化曲线，其中，卡瓣的阻力系数定义为

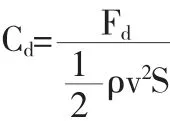
式中，Fd为卡瓣的阻力，ρ为空气密度，v为空气粘性，S卡瓣的投影面积.

由图5可见，卡瓣翻转过程中，阻力系数随翻转角度变化的曲线呈现先上升，再下降，然后再上升，最后下降的趋势.对于阻力系数而言，当翻转角度为0°、180°和360°时，阻力系数为最小值0.2，当翻转角度为90°和270°时，阻力系数为最大值1.4.由此可见，当卡瓣以出口状态弹出时，其受升力最大；当卡瓣以竖直向上状态（翻转角度为90°和270°）时，其升力最小.从图中还可以看出，卡瓣的阻力系数以0.8为中心，以0.6为振幅，以180°为周期，进行周期性变化.

图6为为不同翻转角度下卡瓣的力矩系数变化曲线，其中，卡瓣的力矩定义为

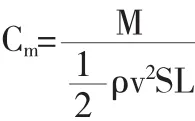
上式中，M为卡瓣的力矩，力矩中心位于卡瓣的质心，ρ为空气密度，v为空气粘性，S卡瓣的投影面积，L为卡瓣的最大直径.

从图6中可以看出，卡瓣翻转过程中，其升力系数随翻转角度变化的曲线呈现先上升，再下降，最后上升的趋势.对于力矩系数而言，当迎角为120°时，力矩系数最大为0.7；当迎角为240°时，力矩系数为最小值-0.8.卡瓣的力矩系数在360°范围内，以-0.5为中心，以0.75为振幅，进行周期性变化.

图3 不同角度下卡瓣表面压力云图

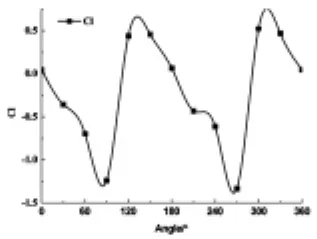
图4 升力系数变化曲线

图5 阻力系数变化曲线

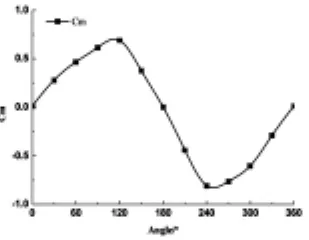
图6 力矩系数变化曲线

4 结论

从文中结果分析来看，本文建立的数值方法是可靠的，可以用于分析卡瓣翻转过程中的气动特性.从气动特性曲线可见，卡瓣的升力系数、阻力系数和力矩系数随翻转角度的变化均符合周期性变化趋势，它们都是以某一特定值为中心和振幅，进行周期性变化.卡瓣的升力系数以-0.25为中心，以1.05为振幅和180°为周期，进行周期性变化；卡瓣的阻力系数以0.8为中心，以0.6为振幅，以180o为周期，进行周期性变化；卡瓣的力矩系数在360o范围内，以-0.5为中心，以0.75为振幅，进行周期性变化.

〔1〕武频，尚伟烈，赵润祥，陈纯.APFSDS弹托分离干扰三维流场数值模拟[J].空气动力学报,2005,23(1):1-4.

〔2〕SCHMIDT EM,SHEAR D D.Aerodynamic interference during sabot discard[J].AIAA Journal of Spacecraft and Rockets,1978,15(3):162-167.

〔3〕武频,赵润祥,张笑.脱壳穿甲弹弹托分离二维数值模拟[J].弹箭与制导学报,2001,21(2):27-29.

〔4〕谭俊杰,张军,武频.网格生成方法在APFSDS及弹托干扰流场计算中的应用[J].弹道学报,2002,14(1):41-43.

〔5〕HUANG Zhen-gui,wessam Mahfouz Elnaggar,CHEN Zhi-hua.Numerical investigation of the three-dimensional dynamic process of sabot discard [J].Journal of mechnical science and technology,2014,28(7):2637-2649.

〔6〕胡晓磊，盛文成，乐贵高，聂贇.车载导弹垂直发射系统双面导流器的研究[J].火力指挥与控制,2013,38(11):53-55.

〔7〕Shi T H.A new k-ε Eddy-viscosity model for high Reynolds number turbulent flows-model development and validation[J].Computers&Fluids，1995，24(3)：227-238.

〔8〕Yang,S.L.Y.L.Chang,O.Arici.Incompressible Navier- Stokes Computation of the NREL Airfoils Using a Symmetric Total Variational Diminishing Scheme of Solar Energy Engineering[J].1994,116(4): 174-182.

〔9〕杨琪,郭佳肄,胡晓磊.喷水对燃气-蒸汽弹射内弹道影响数值研究[J].赤峰学院学报(自然科学版),2016,32(7):191-192.

TJ0

：A

：1673-260X（2017）05-0119-02

2017-01-23

安徽高校自然科学研究项目：障碍物抑制初容室内二次燃烧机理研究（KJ2017A062）