基于ALE算法的隧道开挖爆破振动特性数值分析
王 峥 峥, 张 杨 生
( 大连理工大学 土木工程学院, 辽宁 大连 116024 )
基于ALE算法的隧道开挖爆破振动特性数值分析
王 峥 峥*, 张 杨 生
( 大连理工大学 土木工程学院, 辽宁 大连 116024 )
基于ANSYS/LS-DYNA软件,分析隧道开挖过程中爆破振动对围岩及初期支护的影响.为了使数值模拟能够真正反映实际情况,采用更精确合理的爆炸数值计算方法:利用软件内置炸药模块和状态方程模拟爆破荷载的作用,并采用ALE算法模拟炸药与岩石之间的接触关系.在ALE算法中,为防止爆炸过程中网格的过分畸变给结果带来不利影响,将炸药定义成流体.分析结果表明:应力、速度均在爆炸发生的极短时间内达到峰值,而后迅速衰减,10 ms 后达到稳定状态.上台阶爆破在围岩拱顶处产生的水平振速峰值为下台阶爆破的6倍左右,在拱脚位置约为0.88倍;上台阶爆破在围岩拱顶处产生的竖直振速峰值为下台阶爆破的8倍左右.下台阶爆破在围岩拱顶处产生的应力峰值是上台阶爆破的1/5,在拱脚处相差不大;同一位置,初期支护结构质点振速峰值与单元应力峰值均比围岩大.
状态方程;数值模拟;ALE算法
0 引 言
城市地铁区间隧道开挖中多采用钻爆法进行硬岩地区的施工,其中,台阶法具有适应性广、造价低等优点,被广泛应用于城市浅埋隧道爆破施工中[1].地铁线路经过城市繁华地带,会穿过商业区和居民区,地面环境比较复杂,爆破产生的振动、噪声会给周围居民的日常生活带来不便.另外,城市隧道埋深较浅,爆破产生的次生影响最主要的就是振动效应[2].因此控制爆破振动效应是施工顺利进行的有效保证[3-4].
迄今,国内外学者对隧道围岩的物理力学特性进行了大量的研究.譬如,Tiwari等建立了钢筋混凝土衬砌隧道内部爆炸的三维非线性有限元分析模型,研究受到内部爆破荷载作用的风化岩体隧道的动态响应[5];Wang等建立了能够模拟爆炸和冲击波在土中传播的三相土壤模型[6-7];运用该模型,Wang等进行了地下结构在地下爆炸作用下的结构响应的完全耦合数值模拟[8];黄达等通过FLAC数值模拟与监测资料相结合,从不同位置、抗剪强度和地应力场等因素方面,较详细地分析了地下洞室围岩应力、变形及稳定性分布影响规律[9];耿萍等将LS-DYNA软件与振动台试验结合,在地震作用下,研究了穿越断层破碎带隧道衬砌结构的内力分布规律及其与断层间的距离关系,验证了数值模拟结论的准确性[10].
本文以大连地铁学苑广场站—海事大学站区间隧道为背景,采用数值模拟方法,借助有限元软件ANSYS/LS-DYNA建立隧道上、下台阶爆破开挖的三维有限元模型,分析爆破荷载作用下围岩的振动特性以及下台阶爆破对上部初期支护的影响.
1 工程概况

2 数值模型
2.1 模型说明
采用ANSYS/LS-DYNA有限元软件建立三维模型,将隧道掘进方向作为Z轴,竖直方向作为Y轴,水平方向作为X轴.结合圣维南原理以及实际工程情况,利用ANSYS/LS-DYNA软件建立横向长×高×纵向长=70 m×40 m×8 m的数值计算模型.计算模型如图1所示.其中隧道区域网格进行了局部加密.

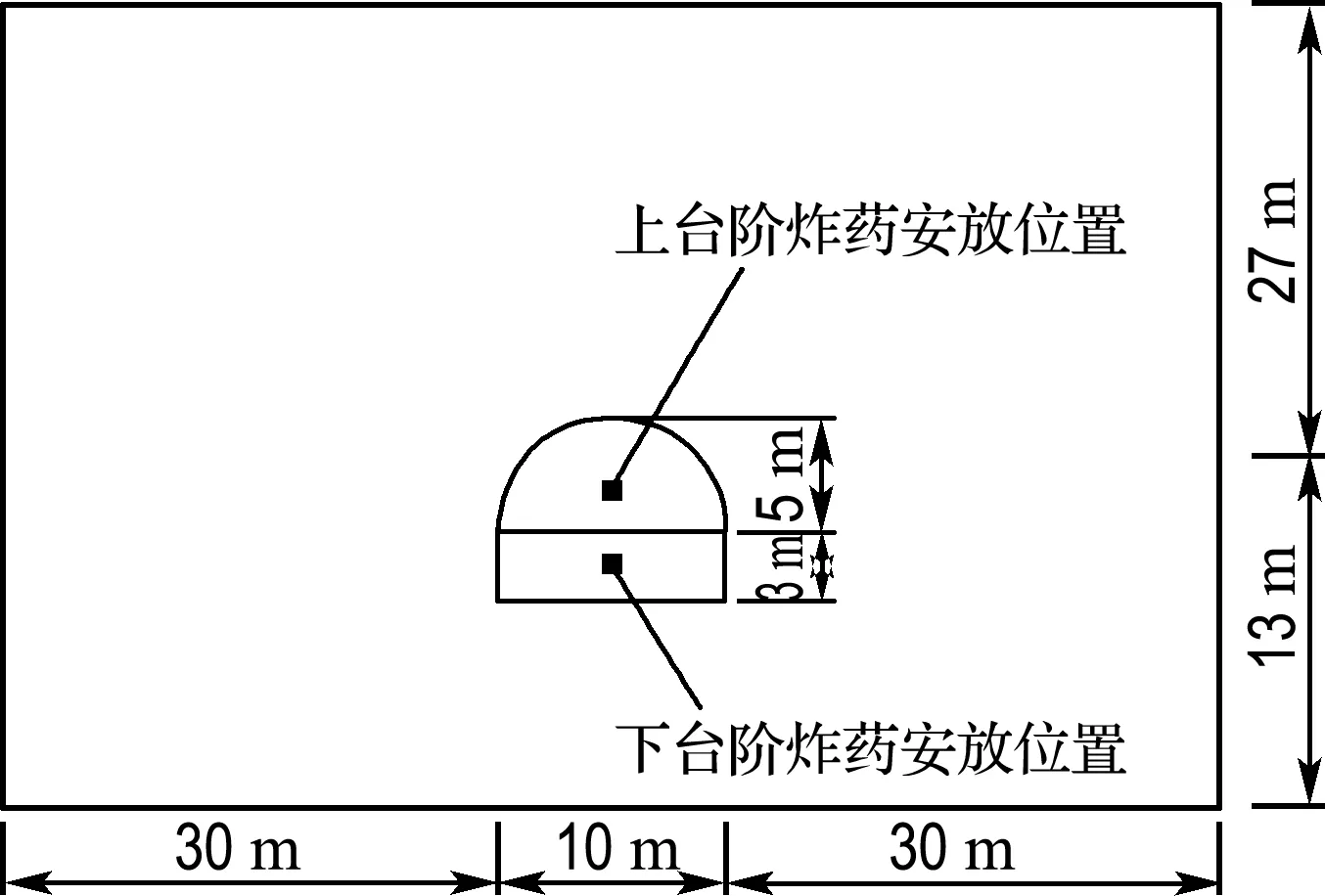
(a) 尺寸

(b) 网格
图1 隧道计算模型
Fig.1 Calculation model of the tunnel
整个数值计算模型包含围岩、炸药和初期支护.本次计算只考虑隧道掏槽爆破,炸药采取集中装药的方式,装药位置如图1(a)所示.
2.2 边界处理
整个数值模拟计算过程分为静力分析和动力分析两部分.其中,静力分析时,模型前、后、左、右四个面均设置为水平约束,模型的底部设置为固定约束,模型上表面设为自由边界,而且考虑重力作用.进行动力分析时,模型的上部、洞口所在面施加自由边界条件,且不计上部荷载,其余4个面边界施加固定约束,为防止应力波反射对计算结果的影响,全部设为无反射边界[11].
2.3 理论算法和材料选择
2.3.1 ALE算法介绍 ALE算法的核心是方程的求解不受模型材料的变形和移动的影响,在其独立的网格上进行计算.这种方法解决了材料变形过大对计算结果的影响,同时解决了移动边界产生的一些难以解决的问题.
以网格中包含物质种类的多少为依据,ALE算法分为单物质算法和多物质算法两种.多物质ALE算法中,物质的交换可以在相应单元中进行[12].隧道爆破开挖下结构的动力响应涉及岩石、空气和炸药等多种物质,计算过程中物质发生较大变形,网格也相对变化较大,因此必须重视解决大变形带来的影响.
ALE算法允许炸药、岩石和空气自由穿梭于彼此间,通过物质的流动可以分析爆炸发生的过程.其能够很好地避免计算中网格变形过大导致的计算中断问题.因此,ALE算法能够很好地应用于爆炸分析计算中.
2.3.2 炸药燃烧模型 LS-DYNA软件本身就含有模拟炸药爆炸的相应单元,通过状态方程控制炸药材料,在模拟炸药爆炸时,压力和比容的关系可以通过如下JWL状态方程来描述:
(1)
式中:p为压力;V为相对体积;E0为初始比热力学能;参数A、B、R1、R2、ω为试验确定的常数.本文选取的炸药参数如表1所示.
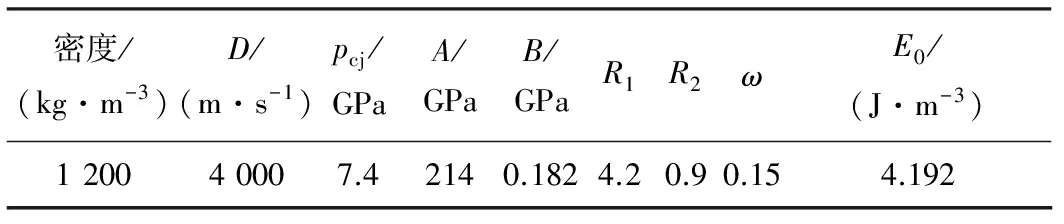
表1 炸药参数
2.3.3 岩石材料弹塑性模型 炸药爆炸时靠近爆源的岩体有明显的应变率效应,极易发生屈服而导致岩体破碎,采用包含应变率的塑性随动模型(MAT_PLASTIC_KINEMATIC)经证明是比较合适的[13].表2给出了岩石材料参数.
2.3.4 初期支护材料模型 初期支护应采用喷射混凝土的支护形式,模型采用软件自带的损伤本构模型(*MAT_JOHNSON_HOLMQUIST_CONCRETE),材料参数见表3.

表2 岩石参数
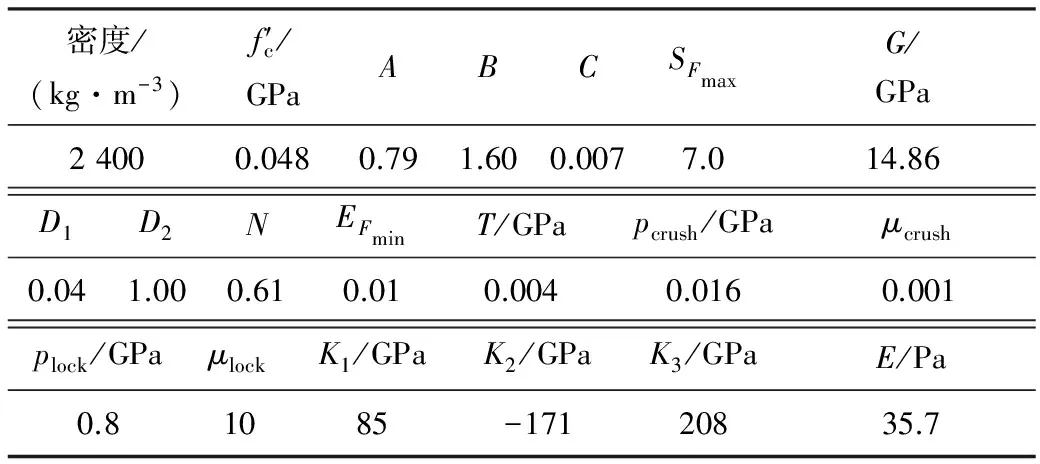
表3 混凝土H-J-C模型材料参数
3 数值计算结果及其分析
3.1 控制节点与单元的选取
数值模拟的重点是对隧道开挖面拱顶及拱脚节点振速和单元应力的数据分析.关键测点及单元Z向坐标值为掌子面处,布置在拱顶及拱脚位置,测点位置标号1、2、3,如图2所示.
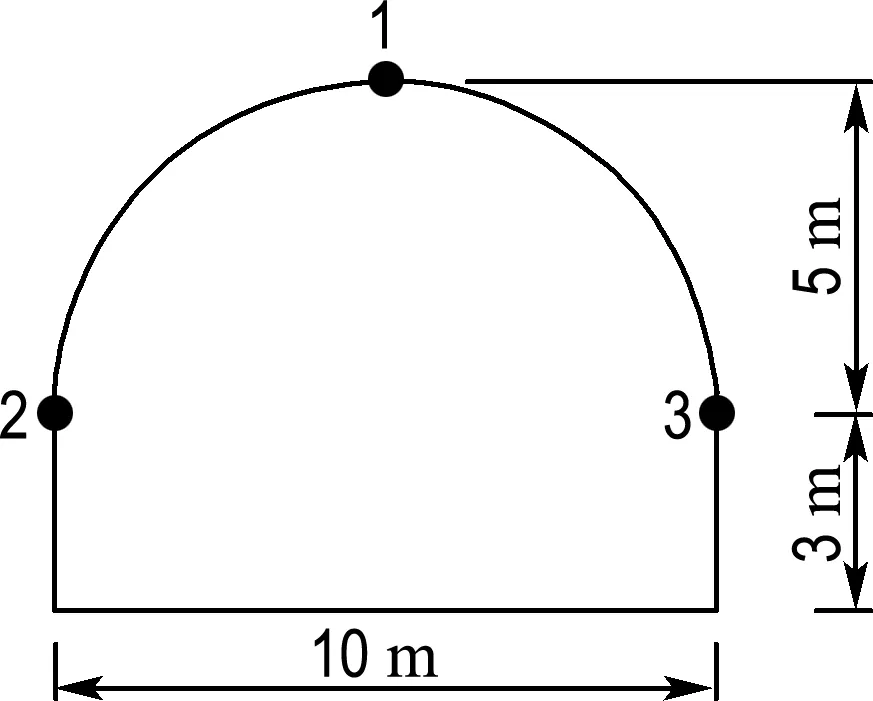
图2 控制点位置布置图
3.2 模拟结果及分析
3.2.1 振动速度分析
(1)由于2、3号测点关于炸药中心对称,上台阶爆破后只提取1、2号两个测点处围岩节点振速时程曲线,如图3所示.可以看出,在爆破应力波的作用下,节点振速在极短时间内达到峰值,而后迅速衰减.其中,拱顶处水平方向振速峰值为 0.17 m/s,到达时刻1 ms,竖直方向振速峰值为1.87 m/s,到达时刻2 ms;拱脚处水平方向振速峰值为0.35 m/s,到达时刻2 ms,竖直方向振速峰值为0.25 m/s,整个过程速度变化较小.爆破应力波产生的振动主要集中在爆破发生后10 ms内.


(a) 水平方向
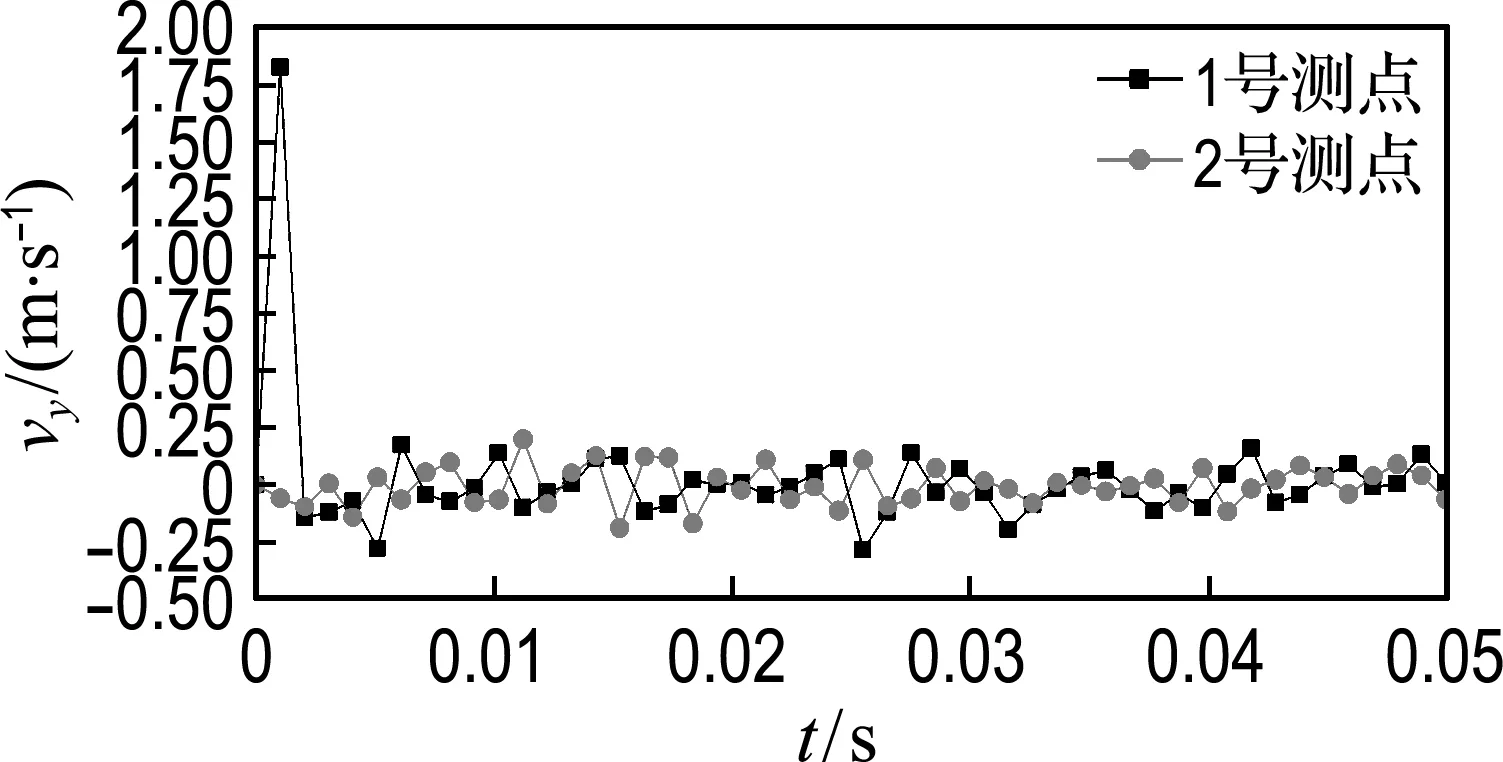
(b) 竖直方向
图3 上台阶爆破后振速时程曲线
Fig.3 The time history curve of velocity under blasting on the upper-step
(2)下台阶爆破后提取2个测点处围岩节点振速时程曲线,如图4所示.由图可以看出,在爆破应力波的作用下,节点振速在较短时间内达到峰值,而后迅速衰减至趋于0.其中,拱顶处水平振速峰值为0.03 m/s,整个过程振动幅度较小,竖直振速峰值为0.24 m/s;拱脚处水平振速峰值为0.40 m/s,竖直振速峰值为0.30 m/s.

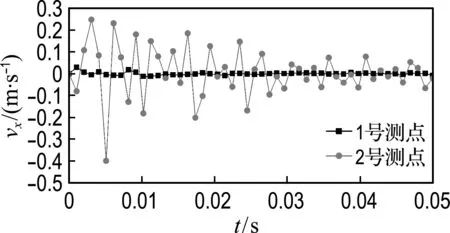
(a) 水平方向
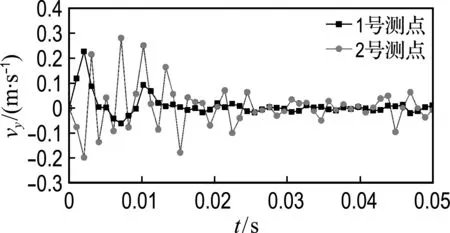
(b) 竖直方向
图4 下台阶爆破后振速时程曲线
Fig.4 The time history curve of velocity under blasting on the lower-step
对比图3和图4,可以看出,下台阶爆破后拱顶处节点水平方向峰值振速约为上台阶爆破后产生的节点振速的0.18倍,竖直方向峰值振速约为上台阶爆破后产生的节点振速的0.13倍,爆破振动均主要集中在爆破后的10 ms内;拱脚处振动结果相比,下台阶爆破产生的峰值振速比上台阶爆破产生的峰值振速大一些.两次爆破后,质点振速时程曲线变化趋势相似,均是在短时间内达到振速峰值,后迅速衰减,最后趋近于0.
(3)下台阶爆破后提取2个测点对应初期支护处节点振速时程曲线,如图5所示.由图5可以看出,在1 ms左右,拱顶处水平方向振速峰值达到最大,约为0.05 m/s,整个过程振速接近于0,竖直方向振速峰值约为0.20 m/s;在3 ms左右,拱脚处水平振速峰值达到最大,约为0.62 m/s,15 ms以后趋于0,竖直方向振速峰值约为0.48 m/s,15 ms以后趋于0.

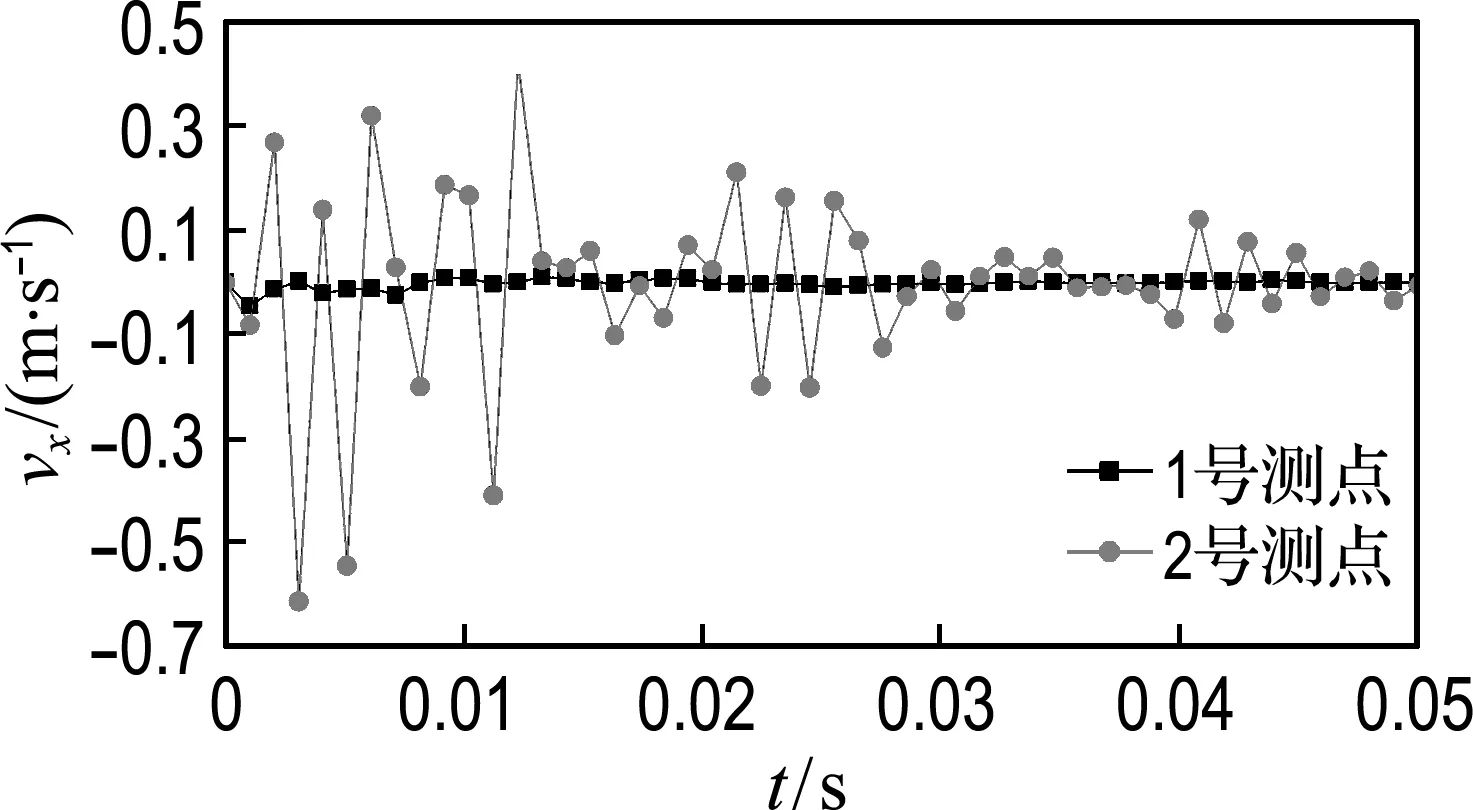
(a) 水平方向
(b) 竖直方向
图5 下台阶爆破后支护振速时程曲线
Fig.5 The time history curve of the supporting velocity under blasting on the lower-step
对比图4和图5可以看出,下台阶爆破后,同一位置初期支护质点振速峰值大于围岩质点振速峰值,为其1.5倍左右.
3.2.2 单元应力分析
(1)上台阶爆破后提取2个测点处围岩单元应力时程曲线,如图6(a)所示.由图可以看出,在爆破应力波的作用下,单元应力在极短时间内达到峰值,而后迅速衰减,短时间内达到稳定状态.其中,拱顶处单元应力峰值为14.4 MPa,到达时刻2 ms,拱脚处单元应力峰值为12.6 MPa,到达时刻2 ms,爆破应力波产生的应力变化主要集中在爆破发生后的10 ms内.
(2)下台阶爆破后提取2个测点处围岩单元应力时程曲线,如图6(b)所示.由图可以看出,在爆破应力波的作用下,拱顶单元应力在4 ms达到峰值3.1 MPa,而后迅速衰减至1 MPa左右,达到稳定状态.拱脚处单元应力在2 ms达到峰值11.0 MPa,是拱顶处的3.5倍左右,而后迅速衰减至5 MPa以下,达到稳定状态.

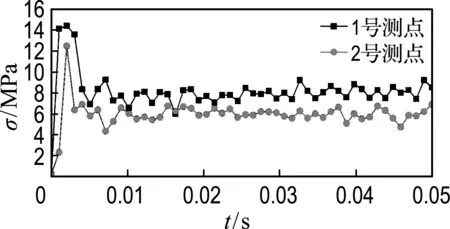
(a) 上台阶爆破
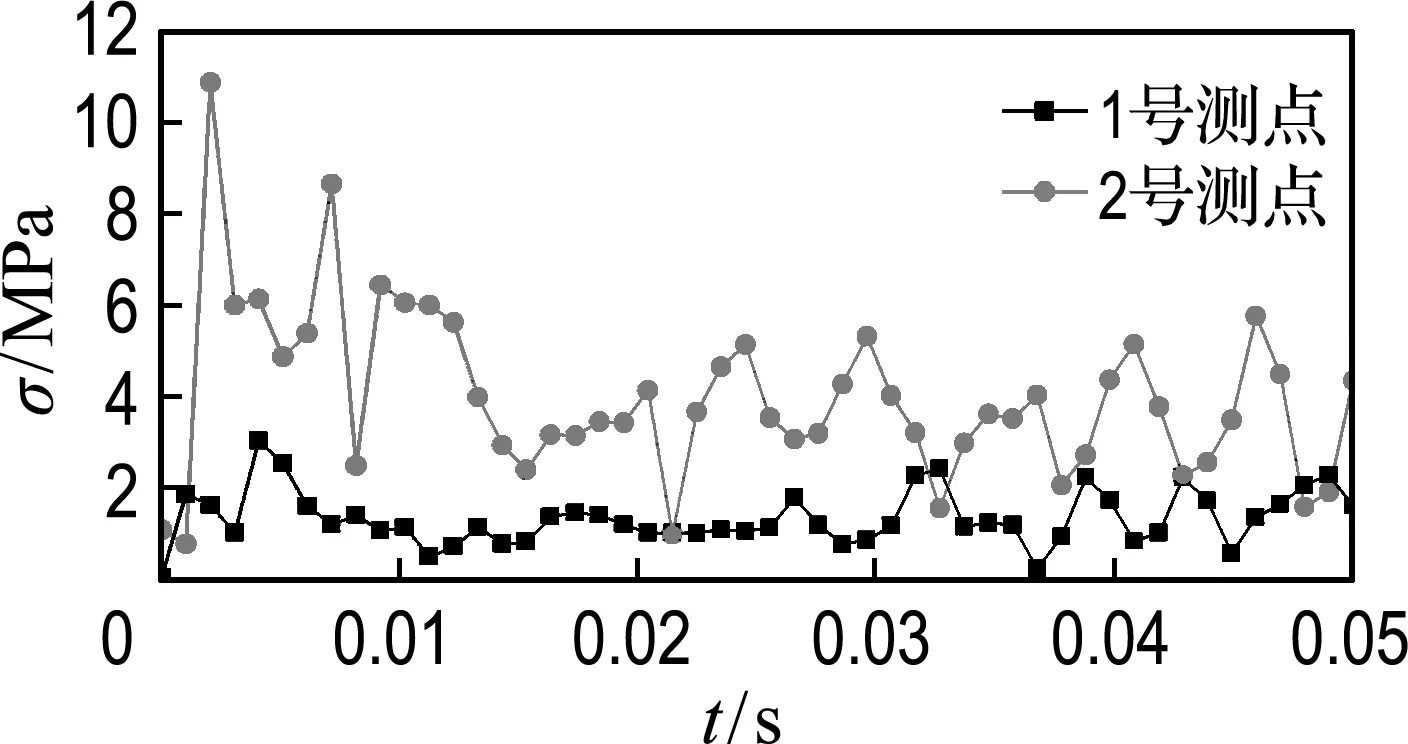
(b) 下台阶爆破
图6 上、下台阶爆破后应力时程曲线
Fig.6 The time history curve of stress under blasting on the upper-step and lower-step
对比图6(a)和(b)可以看出,下台阶爆破后拱顶处单元应力峰值约为上台阶爆破后产生的单元应力峰值的0.22倍,到达峰值的时刻延迟2 ms;拱脚处单元应力结果相比,下台阶爆破产生的峰值应力是上台阶爆破产生的峰值应力的0.87倍左右,到达峰值时刻相同.单元应力变化均集中在爆破后的10 ms内.
(3)下台阶爆破后提取2个测点对应初期支护处单元应力时程曲线,如图7所示.由图可以看出,在爆破应力波的作用下,拱顶单元应力在7 ms 内达到峰值23 MPa,10 ms后衰减至20 MPa,达到稳定状态.拱脚处单元应力在3 ms内达到峰值30 MPa,是拱顶处的1.3倍左右,最后稳定在10 MPa上下波动.

图7 下台阶爆破后支护应力时程曲线
对比图6(b)和图7可以看出,下台阶爆破后,同一位置围岩单元应力峰值远小于初期支护单元应力峰值.
提取了围岩及初期支护结构关键位置处节点振速时程曲线和单元应力时程曲线,表4给出了所有情况下的峰值.由表可知,上台阶爆破时,围岩拱顶节点水平方向振速远小于竖直方向振速,而拱脚节点水平方向振速大于竖直方向振速;单元应力相差1.8 MPa,应重点监控拱顶竖直方向和拱脚水平方向振动速度;下台阶爆破时,围岩、支护拱顶节点振速和单元应力均小于拱脚位置,同一位置围岩应力远小于支护应力,应重点监控支护结构上的应力变化.

表4 峰值结果对比表
4 结 论
(1)上台阶爆破产生的节点水平、竖直振速峰值在围岩拱顶处远大于下台阶爆破产生的节点振速峰值,约为其5~8倍.爆破后,围岩振速在极短时间内达到峰值,而后迅速衰减,振动持续10 ms以后,振速趋于0.
(2)上台阶爆破产生的单元应力峰值在围岩拱顶处大于下台阶爆破产生的单元应力峰值,约为其5倍;在拱脚处,下台阶爆破产生的单元应力峰值与上台阶爆破产生的单元应力峰值相差微小,仅差1.6 MPa.爆破后,围岩单元应力在极短时间内达到峰值,而后迅速衰减,10 ms后达到稳定状态.
(3)下台阶爆破后,同一位置初期支护产生的振速峰值比围岩的大,约为其1.5倍;单元应力峰值比围岩的大,约为其3~7倍.
(4)根据模拟结果,在上台阶爆破施工时,应加强拱顶、拱脚位置的监测和超前支护;下台阶爆破施工时,应加强支护结构的监测和保护.
[1] 闫鸿浩,王小红. 城市浅埋隧道爆破原理及设计[M]. 北京:中国建筑工业出版社, 2013.
YAN Honghao, WANG Xiaohong. Urban Shallow Tunnel Blasting Theory and Design [M]. Beijing: China Architecture & Building Press, 2013. (in Chinese)
[2] 刘 琳,明 峰. 地铁隧道掘进爆破振动效应研究[J]. 公路, 2012(8):262-266.
LIU Lin, MING Feng. The research on subway tunnel excavation blasting vibration effect [J]. Highway, 2012(8):262-266. (in Chinese)
[3] 林学义,王兰民. 隧洞的爆破地震动效应问题[C]// 工程爆破文集第六集. 深圳:海天出版社, 1997.
LIN Xueyi, WANG Lanmin. The tunnel blasting seismic effect [C] // Proceedings of Engineering Explosive: vol.6. Shenzhen: Haitian Publishing House, 1997. (in Chinese)
[4] 钱七虎,陈士海. 爆破地震效应[J]. 爆破, 2004, 21(2):1-5.
QIAN Qihu, CHEN Shihai. Blasting vibration effect [J]. Blasting, 2004, 21(2):1-5. (in Chinese)
[5] TIWARI R, CHAKRABORTY T, MATSAGAR V. Dynamic analysis of a twin tunnel in soil subjected to internal blast loading [J]. Indian Geotechnical Journal, 2016, 46(4):369-380.
[6] WANG Zhongqi, LU Yong. Numerical analysis on dynamic deformation mechanism of soils under blast loading [J]. Soil Dynamics and Earthquake Engineering, 2003, 23:705-714.
[7] WANG Zhongqi, HAO Hong, LU Yong. A three-phase soil model for simulating stress wave propagation due to blast loading [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(1):33-56.
[8] WANG Zhongqi, LU Yong, HAO Hong,etal. A full coupled numerical analysis approach for buried structures subjected to surface blast [J]. Computers & Structures, 2005, 83:339-356.
[9] 黄 达,黄润秋,张永兴. 断层位置及强度对地下洞室围岩稳定性影响[J]. 土木建筑与环境工程, 2009, 31(2):68-73.
HUANG Da, HUANG Runqiu, ZHANG Yongxing. Analysis on influence of fault location and strength on deformation and stress distribution of surrounding rocks of large underground openings [J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(2):68-73. (in Chinese)
[10] 耿 萍,吴 川,唐金良,等. 穿越断层破碎带隧道动力响应特性分析[J]. 岩石力学与工程学报, 2012, 31(7):1406-1413.
GENG Ping, WU Chuan, TANG Jinliang,etal. Analysis of dynamic response properties for tunnel through fault fracture zone [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1406-1413. (in Chinese)
[11] 何忠明,蔡 军,王利军,等. 地铁隧道爆破开挖引起地表位移沉降的数值模拟[J]. 中南大学学报(自然科学版), 2015, 46(9):3496-3502.
HE Zhongming, CAI Jun, WANG Lijun,etal. Numerical simulation of ground subsidence due to tunnel blasting excavation [J]. Journal of Central South University (Science and Technology), 2015, 46(9):3496-3502. ( in Chinese)
[12] 贾祖朋. 基于MOF界面重构的多物质ALE方法[J]. 计算物理, 2010, 27(3):353-360.
JIA Zupeng. A multi-material arbitrary Lagrangian-Eulerian method based on MOF interface reconstruction [J]. Chinese Journal of Computational Physics, 2010, 27(3):353-360. (in Chinese)
[13] 夏 祥. 爆炸荷载作用下岩体损伤特征及安全阈值研究[D]. 武汉:中国科学院武汉岩土力学研究所, 2006.
XIA Xiang. Study on damage characteristic and safety threshold of rock vibration by blast [D]. Wuhan:Institute of Rock and Soil Mechanics of the Chinese Academy of Sciences, 2006. (in Chinese)
Numerical analysis for blasting vibration characteristics in tunnel excavation based on ALE algorithm
WANG Zhengzheng*, ZHANG Yangsheng
( School of Civil Engineering, Dalian University of Technology, Dalian 116024, China )
Based on ANSYS/LS-DYNA software, the influences of blasting vibration in tunnel excavation on surrounding rock and initial support structure are analyzed. In order to make the numerical simulation truly reflect the actual situation, a more accurate method of explosion simulation is adopted. The built-in explosives module in software and equation of state are used to simulate the explosive loads. In the meantime, the ALE algorithm is used to simulate the contact relationship between the structure of explosives and rocks. In ALE algorithm, explosives are defined into the fluid in order to avoid excessive grid distortion caused by explosion, which adversely affects the result of the calculation. The analytical results show that: Stress and velocity all reach a maximum within a very short period of time after the blasting, and then decay to the stable state at 10 ms. The peak value of horizontal vibration velocity at the dome roof of the surrounding rock of the upper-step blasting is about 6 times that of the lower-step blasting, and about 0.88 times at the arch foot position. The vertical vibration velocity peak value at the dome roof of the surrounding rock of upper-step blasting is about 8 times that of the lower-step blasting. The peak value of stress generated by the lower-step blasting at the dome roof of the surrounding rock is 1/5 of the upper-step blasting, and the difference is small at the arch foot. At the same position, the peak value of mass point vibration velocity and element stress of primary support structure are larger than those of surrounding rock.
equation of state; numerical simulation; ALE algorithm
1000-8608(2017)03-0279-06
2016-08-15;
2017-04-10.
住建部科技项目(2014-K5-005);大连市建委科技项目(052033).
王峥峥*(1982-),男,博士,副教授,E-mail:wangzhengzheng@dlut.edu.cn;张杨生(1989-),男,硕士生,E-mail:1120837032@qq.com.
TU443
A
10.7511/dllgxb201703010

