德杰尼斯五后问题泛化研究
李 盘 林, 赵 铭 伟, 徐 喜 荣, 李 丽 双, 李 伯 章
( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024;2.滑铁卢大学 计算机工程系, 加拿大 安大略 滑铁卢 )
德杰尼斯五后问题泛化研究
李 盘 林*1, 赵 铭 伟1, 徐 喜 荣1, 李 丽 双1, 李 伯 章2
( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024;2.滑铁卢大学 计算机工程系, 加拿大 安大略 滑铁卢 )
在德杰尼斯五后问题求解方法基础上,给出了2p×2p棋盘坐标表示,定义了方环和马步格,并利用皇后控制数或剩余控制数、皇后最佳(极佳)位置或剩余最佳(极佳)位置,以及棋盘对称性,得到了德杰尼斯五后问题泛化求解定理和便于求解的简化定理.
德杰尼斯五后问题;皇后控制数或剩余控制数;皇后最佳(极佳)或剩余最佳(极佳)位置;方环;马步格
0 引 言
在德杰尼斯五后问题求解方法[1](下称五后问题)一文的结语中,指出对于2p×2p(p=1,2,…)棋盘上最少放置多少皇后,使它们在不同行、不同列和不同对角线上且能吃掉(或称管控)棋盘上其余任何棋子(下称五后问题泛化论题)这一问题的求解途径[2],它可极大限度地克服以往人们用视察法求解[3]的盲目性.随着p的增大,收效更加明显.本文进一步详细地研究五后问题泛化论题.
1 求解前准备
(1)2p×2p棋盘坐标表示:完全类似于文献[1]中的描述,见图1.
(2)方环的定义:由格sp,p,sp+1,p,sp+1,p+1和sp,p+1组成p级方环;由格sp-1,p-1,sp,p-1,sp+1,p-1,sp+2,p-1,sp+2,p,sp+2,p+1,sp+2,p+2,sp+1,p+2,sp,p+2,sp-1,p+2,sp-1,p+1,sp-1,p组成p-1级方环…由格s1,1,s2,1,…,s2p,1,s2p,2,…,s2p,2p,…,s2,2p,s1,2p,…,s1,2组成1级方环(或称边界方环).由各级方环中的格所组成的集合,记为Rk,1≤k≤p,如Rp={sp,p,sp+1,p,sp+1,p+1,sp,p+1}.从方环定义可知,方环是对于某些格在棋盘中位置的一种形象描述.
n(Q|si,j)、n(Q|sk,l)设为皇后Q分别放置在si,j和sk,l上的皇后控制数,于是可给出下列定理:

定理2n(Q|si,j∈Rk)=6p-2k-4,k≤p.
定理3 若si,j,sk,l∈Rk,则n(Q|si,j)=n(Q|sk,l),1≤k≤p.
定理4 若si,j∈Rm,sk,l∈Rn,m>n,则n(Q|si,j)>n(Q|sk,l),1≤m,n≤p.
证明略.
定理4表明了皇后放置格离棋盘中心(p,p)越近,其皇后控制数越大.


图1 2p×2p棋盘定义
令C={si,j|1≤i,j≤2p},即C是棋盘上所有格的集合.

证明略.
设Si,j是与格si,j同行、同列和同对角线上所有格集合,则有下面定理:
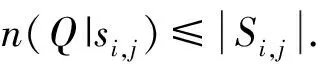

2 核心定理
下面,为凸显放置皇后Q的先后次序,令n(Q|si,j) 是第k个皇后Q放置在si,j上的剩余控制数(k≥2).
设si0,j0=sp,p,其实Rp中任何元素均可作为第1个皇后Q最佳位置.
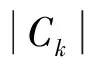
于是,
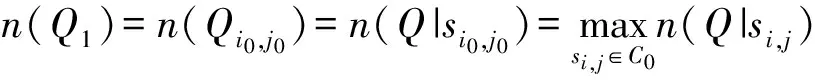
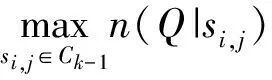
定理7 (五后问题泛化定理)
n(Q1)+n(Q2)+…+n(Qk)+…+n(Qm(p))= 2p×2p
(1)

证明 因为在2p×2p棋盘上要求放置最少皇后,使它们在不同行、不同列和不同对角线上,并能管控(或吃掉)棋盘上除已放置皇后外的任何棋子,这可转化为要求每放置一个皇后,使它管控(或吃掉)棋盘上尽可能多的棋子,并且对于满足下式:
n(Q1)+n(Q2)+…+n(Ql)+…+n(Qmk)= 2p×2p
(1a)
或
n(Q|si0,j0)+n(Q|si1,j1)+…+n(Q|sil-1,jl-1)+…+n(Q|simk-1,jmk-1)=2p×2p
有多个(比如说q个)长度不同的皇后最佳(极佳)位置序列以及由它们分别组成的集S1,S2,…,Sk,…,Sq,而
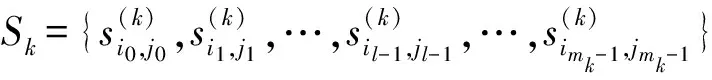
为方便计,每个位置序列称为式(1a)的一个广义解,相应的集合基数,称为广义解长度.

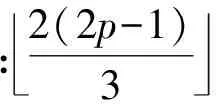
:2(2p-1)3

2
p
-1
,便可确定
m
(
p
).如果在求解中,发现尚有更小的
m
(
p
),则只好改之.然而这种概率是很小的.
为求出所有广义解,首先求出第一个广义解,并以它为基础求出其余广义解.若第一个广义解中有几处皇后剩余极佳位置,对每一处中的每一个其他剩余极佳位置,都按第一个广义解处理皇后剩余极佳位置那样,求出一个新的广义解.对于求出第二个广义解,如同第一个广义解那样处理每个皇后剩余极佳位置,如此这般,便可求出所有广义解.证毕.
推论1 若求得所有以sp,p为第1个皇后Q最佳位置的n(p)个不同基础解,则本定理便有8n(p)个解.
推论

22(2p-1)3 注意,两个不同基础解,是指两个基础解中皇后最佳(极佳)位置或剩余最佳(极佳)位置所组成集合是不同的. 定理8 n(Q1)+n(Q2)+…+n(Qk)+…+n(Qim(p)-1,jm(p)-1)=2p×2p 或 n(Q|si0,j0)+n(Q|si1,j1)+…+n(Q|sik-1,jk-1)+…+n(Q|sim(p)-1,jm(p)-1)= 2p×2p 其中 可知放置第k个皇后在自由域Ck-1=Ck-2-Sik-2,jk-2中求出皇后剩余最佳(极佳)位置sik-1,jk-1,利用马步格,这可转化为 (1)若自由域Ck-1中含有已求出皇后剩余最佳(极佳)位置的马步格,则可求得第k个皇后剩余最佳(极佳)位置sik-1,jk-1,即 (2)若自由域Ck-1中不存在已求出皇后剩余最佳(极佳)位置的马步格,则可在自由域Ck-1中求出第k个皇后剩余最佳(极佳)位置sik-1,jk-1,即 注意:(1)中所求是从第2个开始的皇后剩余最佳(极佳)位置;(2)中所求是几个最后皇后剩余最佳(极佳)位置. 需要指出的是,对于式(1a)求每个广义解均以sp,p为第1个皇后最佳位置,而其余皇后剩余最佳(极佳)位置均在自由域C1,C2,…内求其皇后剩余控制数最大为依据,这便有可能使选定皇后最佳(极佳)位置彼此在棋盘相距远而分散,求得皇后剩余控制数有的较大,有的很小,致使所求广义解长度增大,不利达到基础解要求,期望落空.若皇后最佳(极佳)位置在已选定皇后最佳(极佳)位置的马步格进行,由于这些马步格相聚中心(p,p)周围并逐渐向外展开,使得皇后剩余控制数变动不大,有利于广义解长度缩小而使所要求的基础解可能性增大.因此,定理8是五后问题泛化定理的便于求解的简化形式. 本文定理7和定理8是五后问题泛化研究的两个重要结果,为在n×n网格上布置最少节点管控全局的优化问题提供了一种有效方法,而且在防灾和安全领域及社会管理中得到了应用,有着明显的经济效益和社会效益. [1] 李盘林,赵铭伟,徐喜荣,等. 德杰尼斯五后问题求解方法[J]. 大连理工大学学报, 2016, 56(3):304-308. LI Panlin, ZHAO Mingwei, XU Xirong,etal. Solution to De Jaenisch′s five queens problem[J]. Journal of Dalian University of Technology, 2016, 56(3):304-308. (in Chinese) [2] 李盘林,李丽双,赵铭伟,等. 离散数学[M]. 3版. 北京:高等教育出版社, 2016. LI Panlin, LI Lishuang, ZHAO Mingwei,etal. Discrete Mathematics [M]. 3 rd ed. Beijing: Higher Education Press, 2016. (in Chinese) [3] 李盘林,李立建,刘晓红,等. 基于启发性知识研究生院课表编排系统[J]. 计算机学报, 1992, 15(11):876-889. LI Panlin, LI Lijian, LIU Xiaohong,etal. A heuristic knowledge-based graduate school timetable scheduling system [J]. Chinese Journal of Computers, 1992, 15(11):876-889. (in Chinese) Research on generalization of De Jaenisch′s five queens problem LI Panlin*1, ZHAO Mingwei1, XU Xirong1, LI Lishuang1, LI Bozhang2 ( 1.Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China;2.Department of Computer Engineering, University of Waterloo, Waterloo, ON, Canada ) On the basis of the solution to De Jaenisch′s five queens problem, the coordinate representation of the 2p×2pchess board is introduced, and the square ring and lattice of the horse′s walking in Chinese chess are defined. Using the control number or the remaining control number of the queen, the optimum (heuristically) or the remaining optimum (heuristically) positions of the queen and chess board symmetry, De Jaenisch′s five queens problem generalization solution theorem and the simplified theorem convenient to solve are given. De Jaenisch′s five queens problem; control number/ the remaining control number of the queen; the optimum (heuristically) or the remaining optimum (heuristically) positions of the queen; square ring; lattice of the horse′s walking in Chinese chess 1000-8608(2017)03-0327-04 2016-08-09; 2017-03-31. 国家自然科学基金资助项目(61170303). 李盘林*(1940-),男,教授,E-mail:lipanlin@dlut.edu.cn;赵铭伟(1972-),女,高级工程师,E-mail:zhaomw@dlut.edu.cn;徐喜荣(1967-),女,副教授,E-mail:xirongxu@dlut.edu.cn;李丽双(1967-),女,教授,E-mail:lils@dlut.edu.cn. O158 A 10.7511/dllgxb201703017
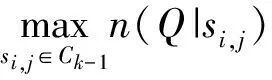
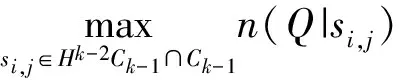
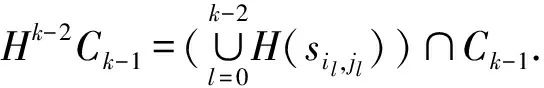
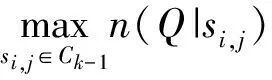
3 结 语

