一类含有4-圈的单圈图一般点可区别全染色
陈 祥 恩, 李 婷, 王 治 文
( 1.西北师范大学 数学与统计学院, 甘肃 兰州 730070;2.宁夏大学 数学计算机科学学院, 宁夏 银川 750021 )
一类含有4-圈的单圈图一般点可区别全染色
陈 祥 恩*1, 李 婷1, 王 治 文2
( 1.西北师范大学 数学与统计学院, 甘肃 兰州 730070;2.宁夏大学 数学计算机科学学院, 宁夏 银川 750021 )
设G为简单图.设f是图G的一个一般全染色,若对图G的任意两个不同的顶点u、v,有C(u)≠C(v),则称f为图G的一般点可区别全染色(简记为GVDTC).对图G进行一般点可区别全染色所需要的最少颜色数称为图G的一般点可区别全色数.将一类含有4-圈的单圈图悬挂边的染色按从小到大的顺序排列,探讨了它的一般点可区别全染色,确定了它具有一般点可区别全染色,并得到了它的一般点可区别全色数.
单圈图;一般全染色;一般点可区别全染色;一般点可区别全色数
0 引 言
点可区别一般边染色是由Harary等于1985年在文献[1]中提出的,文献[2-4]对此也进行了研究.近些年来点可区别的未必正常的全染色也逐渐被研究.例如,点可区别IE-全染色在文献[5]中被提出,而一般点可区别全染色也在文献[6]中被提出.本文受文献[6]的启发,使用更为简单的方法探讨一类含有4-圈的单圈图的一般点可区别全染色,并得到它的一般点可区别全色数.
1 准备工作
图G的一个一般全染色是指若干种颜色对图G的全体顶点及边的一个分配.
设f为图G的一个一般全染色或IE-全染色,x为图G的一个顶点,将在f下x的颜色及与x关联的边的颜色所构成的集合(非多重集)记为Cf(x)或C(x),称之为顶点x在f下的色集合,即C(x)={f(xu)|xu∈E}∪{f(x)}.
设f为图G的一般全染色,若对图G的任意两个不同的顶点u、v,有C(u)≠C(v),则称f为图G的点可区别一般全染色或者一般点可区别全染色(简记为GVDTC).图G的使用了k种颜色的一般点可区别全染色称为图G的k-一般点可区别全染色(简记为k-GVDTC).对图G进行一般点可区别全染色所需要的最少颜色数称为图G的一般点可区别全色数,记为χgvt(G).
星Sn就是完全二部图K1,n(n≥1).称Sm,n是双星,如果Sm,n是树,并且顶点集为V(Sm,n)={ui|i=0,1,…,m}∪{vj|j=0,1,…,n},边集为E(Sm,n)={u0ui|i=0,1,…,m}∪{v0vj|j=0,1,…,n}∪{u0v0},其中m、n是正整数且均大于1.称Sp,q,r是三星,如果Sp,q,r是树,并且顶点集为V(Sp,q,r)={ui|i=0,1,…,p}∪{vj|j=0,1,…,q}∪{wt|t=0,1,…,r},边集为E(Sp,q,r)={u0ui|i=0,1,…,p}∪{v0vj|j=0,1,…,q}∪{w0wt|t=0,1,…,r}∪{u0v0,v0w0},其中p、q、r是正整数且均大于1.
本文设C4;m1,m2,m3,m4表示如图1所示的一类含有4-圈的单圈图.
文献[6]中研究了路、圈、星(即K1,n)、双星、三星、轮、扇、完全图的一般点可区别全染色,确定了它们的一般点可区别全色数.本文将探讨一类含有4-圈的单圈图C4;m1,m2,m3,m4的一般点可区别全染色,并确定它们的一般点可区别全色数.
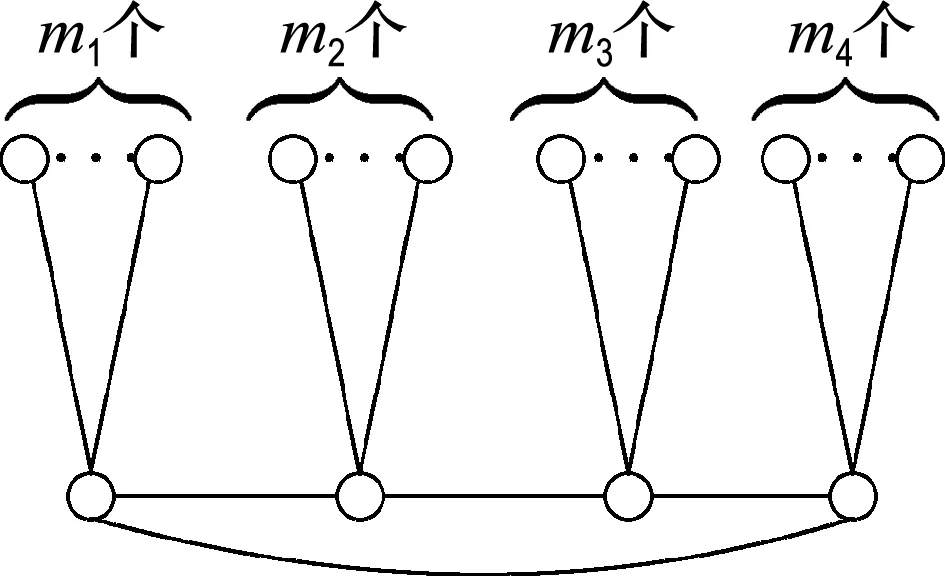
图1 一类含有4-圈的单圈图
引理1[6]设Sn(n≥1)是一个星,则
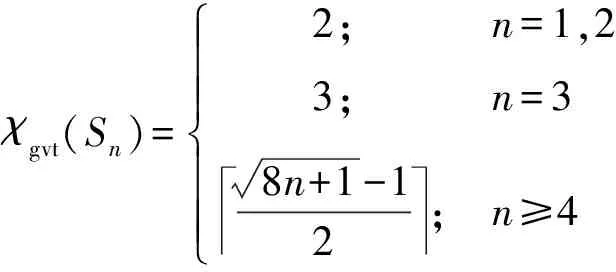
χgvt(Sn)= 2;n=1,23;n=38n+1-12;n≥4ìîíïïïïïï
2 主要结果及其证明
定理1 设C4;m1,m2,m3,m4(mi≥1,i=1,2,3,4)是一个含有4-圈的单圈图,令l=m1+m2+m3+m4,则

χgvt(C4;m1,m2,m3,m4)= 4;l=4,5,68l+1-12;l≥7ìîíïïïï
证明 当l=4时,显然χgvt(C4;1,1,1,1)≥4.因为3种颜色只能区别7个点,而图2(a)给出了C4;1,1,1,1的4-GVDTC,因此χgvt(C4;1,1,1,1)=4.
当l=5时,显然χgvt(C4;1,1,1,2)≥4.因为3种颜色只能区别7个点,而图2(b)给出了C4;1,1,1,2的4-GVDTC,因此χgvt(C4;1,1,1,2)=4.
当l=6时,只需考虑C4;1,1,1,3、C4;1,1,2,2、C4;1,2,1,2即可.显然对这3个图,χgvt≥4,而图2(c)、(d)、(e)分别给出了3个图的4-GVDTC,故χgvt(C4;1,1,1,3)=χgvt(C4;1,1,2,2)=χgvt(C4;1,2,1,2)=4.
以下假设l≥7.
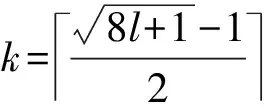
k=8l+1-12
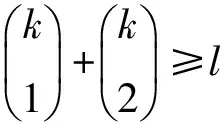
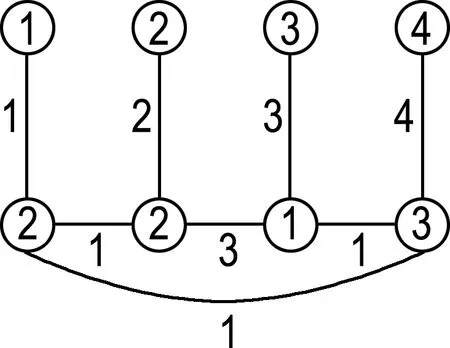
(a) C4;1,1,1,1

(b) C4;1,1,1,2
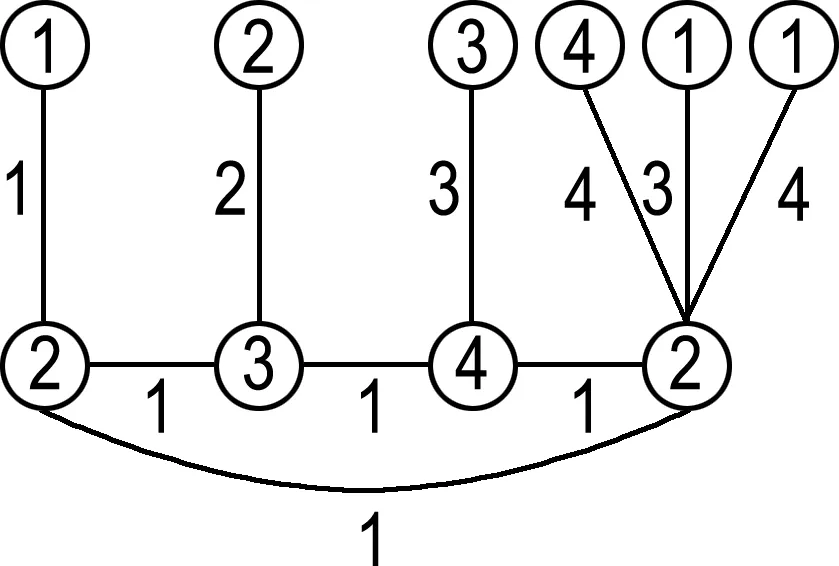
(c) C4;1,1,1,3

(d) C4;1,1,2,2

(e) C4;1,2,1,2
让C4;m1,m2,m3,m4的悬挂点ui,j沿袭在g下G′中对应的悬挂点ui,j的颜色,j=1,2,…,mi,i=1,2,3,4;让C4;m1,m2,m3,m4的悬挂边uiui,j沿袭在g下G′中对应的悬挂边wui,j的颜色,j=1,2,…,mi,i=1,2,3,4.则在此基础上以下只需考虑u1、u1u2、u2、u2u3、u3、u3u4、u4、u1u4的染色即可.
令Aui表示与ui关联的悬挂边的颜色构成的集合(非多重集),i=1,2,3,4.以下分5种情况讨论:
在这种情况下,可按图3(a)、(b)、(c)、(d)、 (e) 所给出的方式分5种情形对圈上的点、边进行染色.比如:在情形(a)中,边u1u2、u2u3、u3u4、u1u4分别用3、4、4、1染色;点u1、u2、u3、u4分别用2、2、3、2染色.这时,Cf(u1)={1,2,3},Cf(u2)={1,2,3,4},Cf(u3)={1,3,4},Cf(u4)={1,2,4},其他顶点即悬挂点的色集合为1-子集或2-子集.因此所得的染色是k-GVDTC.在其他情形下,都可类似得到最终染色是k-GVDTC,且不再赘述.
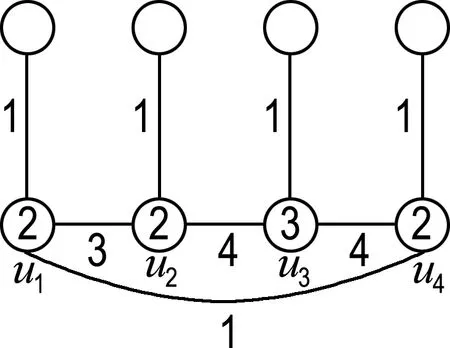
(a)

(b)
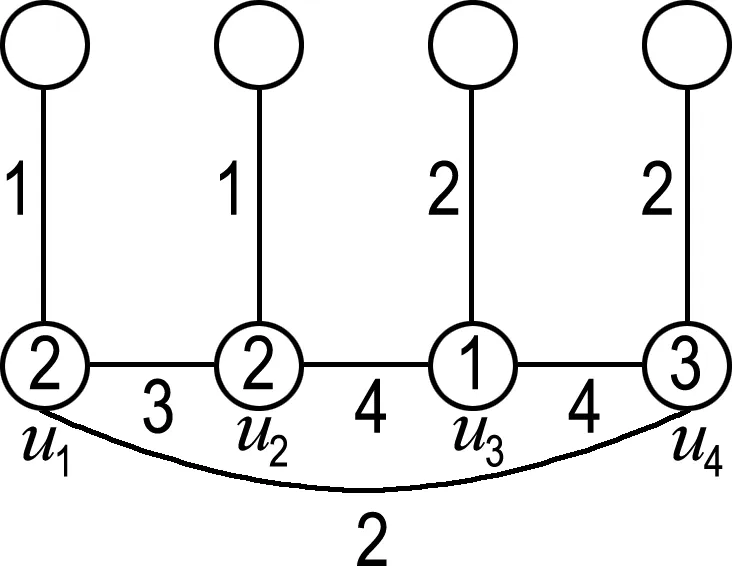
(c)

(d)
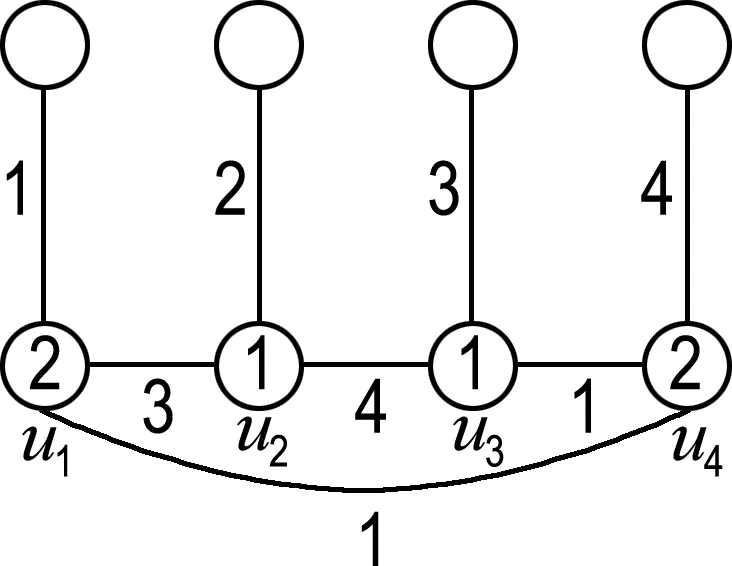
(e)
图3 情况(1)的示意图
Fig.3 The schematic graph of case (1)
情形(a)记为情形(1,1,1,1),情形(b)记为情形(1,1,1,2),其他类似.除上述5种情形外,还有情形(1,2,2,2)等价于情形(b);情形(1,2,2,3)与(1,2,3,3)均等价于情形(d).因此,出现的这些情形将不再画图表示.
注记 图3均为示意图,在图中只标出了与u1、u2、u3、u4关联的悬挂边颜色的种类,而与u1、u2、u3、u4关联的悬挂边的条数不仅仅只有图中出现的条数.后面再出现时,不再作注解.
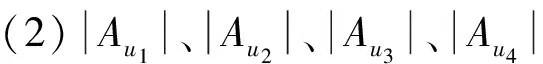
在这种情况下,可按图4所给出的9种方式进行染色.
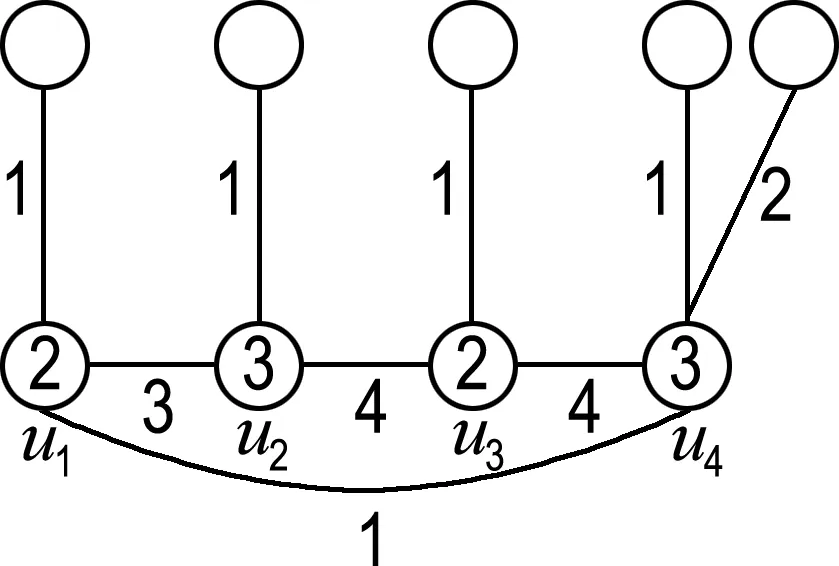
(a)
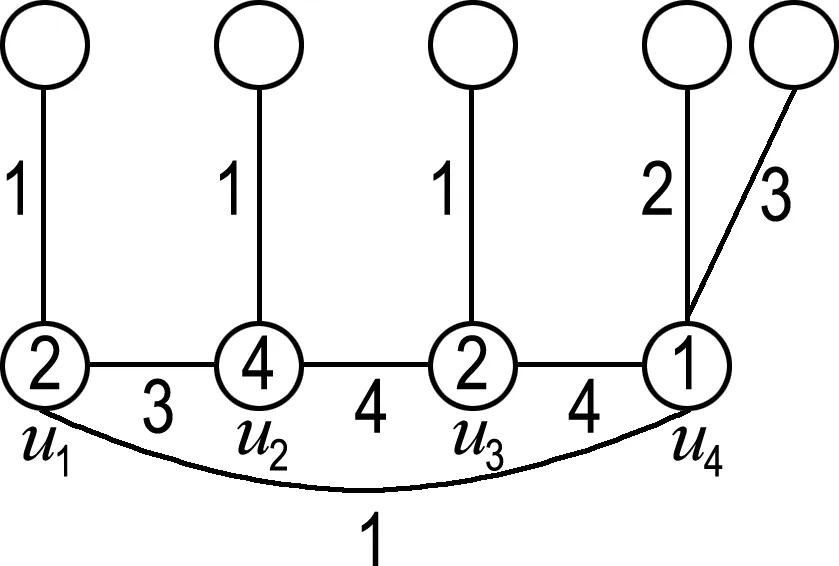
(b)

(c)
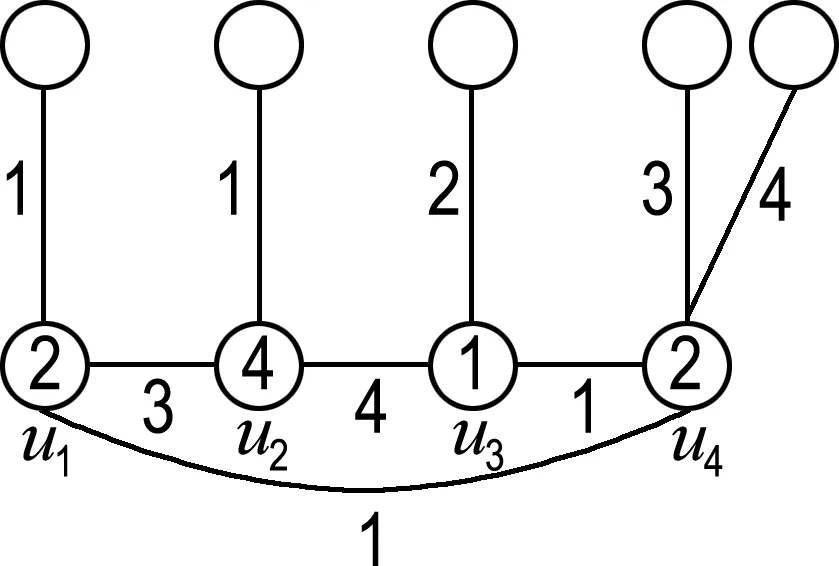
(d)

(e)
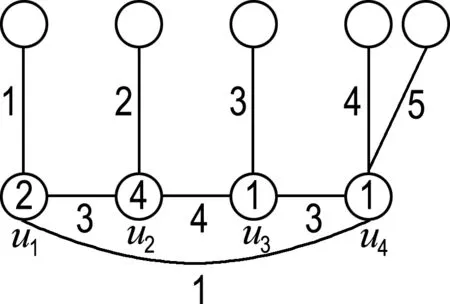
(f)
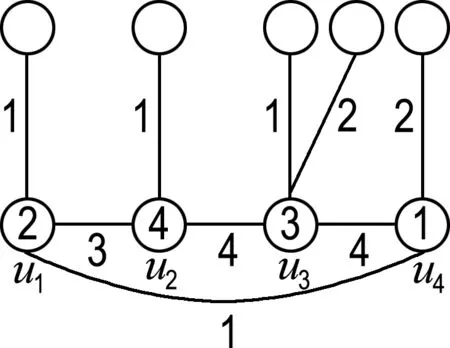
(g)
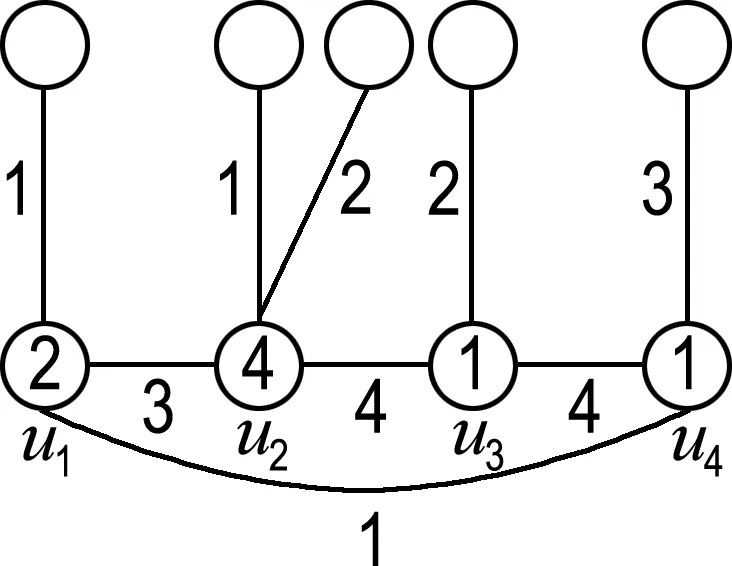
(h)

(i)
图4 情况(2)的示意图
Fig.4 The schematic graph of case (2)
情形(a)记为情形(1,1,1,12),情形(b)记为情形(1,1,1,23),其他类似.除上述9种情形外,还有情形(12,2,2,2)等价于情形(a);情形(12,3,3,3)等价于情形(b);情形(1,1,23,3)、(1,12,3,3)和(1,1,23,3)等价于情形(c);情形(1,2,2,23)、(1,1,23,4)、(1,23,4,4)、(12,3,3,4)和(12,3,4,4)等价于情形(d);情形(1,12,2,2)等价于情形(g);情形(1,2,2,23)、(1,23,3,3)和(12,2,2,3)等价于情形(i);情形(1,2,23,4)、(1,2,34,4)、(1,12,3,4)、(1,23,3,4)和(12,2,3,4)等价于情形(e);情形(1,2,34,5)、(1,23,4,5)和(12,3,4,5)等价于情形(f);情形(1,2,23,3)等价于情形(h).因此,出现的这些情形将不再画图表示.
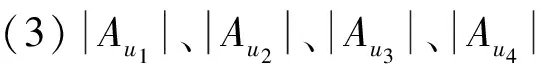
由悬挂边染色规律得,Au3≠Au4,则Au4Au3≠∅且Au3Au4≠∅.设a,b∈Au3且a 由悬挂边染色规律得,Au2≠Au4,则Au4Au2≠∅且Au2Au4≠∅.设a,b∈Au2且a 这时由悬挂边染色规律得,Au2、Au3、Au4互不相同.设Au1={c0},a,b∈Au4,且a 下面用c0染u1u4;用k-1染u1;用k分别去染u1u2、u2、u2u3、u3和u3u4;用{1,2,…,k}{c0,a,b}中某种颜色去染u4.在上述染色下,c0∉Cf(u3),而c0∈Cf(u1)∩Cf(u4),故Cf(u3)≠Cf(ui),i=1,4;Au2≠Au3,k∉Au2∪Au3,故Cf(u2)≠Cf(u3);|Cf(u1)|=3,|Cf(u4)|≥4,故Cf(u1)≠Cf(u4);k-1∈Cf(u1)Cf(u2),故Cf(u1)≠Cf(u2);a∈Cf(u4)Cf(u2),故Cf(u2)≠Cf(u4).因此,所得的染色是C4;m1,m2,m3,m4的k-GVDTC. 这时由悬挂边染色规律得,Au1、Au3、Au4互不相同.设Au2={c0},a,b∈Au1,且a 这时由悬挂边染色规律得,Au1、Au2、Au4互不相同.设Au3={c0},d0∈Au1,a,b∈Au4,且a 下面用k-1染u3;用k分别去染u1、u1u2、u2、u2u3和u3u4;用d0染u1u4;用{1,2,…,k}{a,b,d0}中某种颜色去染u4.可以看出,上述染色是C4;m1,m2,m3,m4的k-GVDTC. 这时由悬挂边染色规律得,Au1、Au2、Au3互不相同.设Au4={c0},d0∈Au1,a,b∈Au3,且a 下面用a染u4;用k分别去染u1、u1u2、u2和u2u3;用d0染u3u4与u1u4;用{1,2,…,k}{a,b,d0}中某种颜色去染u3.可以看出,上述染色是C4;m1,m2,m3,m4的k-GVDTC. 由悬挂边染色规律得,Au1、Au2、Au3、Au4互不相同.设a,b∈Au1且a 在上述染色下,a∈Cf(u1)∩Cf(u4),而a∉Cf(u2)∩Cf(u3),|Cf(ui)|≥3,i=1,2,3,4,故Cf(ui)≠Cf(uj),j=1,4,i=2,3;c∉Cf(u1),而c∈Cf(u4),故Cf(u1)≠Cf(u4);Au2≠Au3,k∉Au2∪Au3,故Cf(u2)≠Cf(u3).因此,所得的染色是C4;m1,m2,m3,m4的k-GVDTC. 综上即得C4;m1,m2,m3,m4的k-GVDTCf. 在本文定理1中,通过探讨一类含有4-圈的单圈图的一般点可区别全染色,证明了它具有一般点可区别全染色,并得到了它的一般点可区别全色数.另外,一类含有4-圈的单圈图是通过在4-圈的基础上加悬挂点得到的,那么这种方法是不是可以继续延续下去,进而得到一类含有n-圈的单圈图(n≥5)的一般点可区别全色数?这就是今后需要继续研究的课题. [1] HARARY F, PLANTHOLT M. The point-distinguishing chromatic index [M] // HARARY F, MAYBEE J S, eds. Graphs and Application. New York: Wiley Interscience, 1985:147-162. [5] CHEN Xiang′en, GAO Yuping, YAO Bing. Vertex-distinguishing IE-total colorings of complete bipartite graphsKm,n(m [6] LIU Chanjuan, ZHU Enqiang. General vertex-distinguishing total colorings of graphs [J]. Journal of Applied Mathematics, 2014, 2014:849748. General vertex-distinguishing total colorings of a family of unicyclic graphs includingC4 CHEN Xiang′en*1, LI Ting1, WANG Zhiwen2 ( 1.College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China;2.School of Mathematics and Computer Sciences, Ningxia University, Yinchuan 750021, China ) LetGbe a simple graph. For a general total coloringfofG, ifC(u)≠C(v) for any two different verticesuandvofG, thenfis called a general vertex-distinguishing total coloring ofG(or GVDTC ofGfor short). The minimum number of colors required in a GVDTC is the general vertex-distinguishing total chromatic number. The general vertex-distinguishing total colorings of a family of unicyclic graphs includingC4are discussed by making the coloring of its pendent edges in an ascending order. It is determined that it has a general vertex-distinguishing total coloring ofGand its general vertex-distinguishing total chromatic number is got. unicyclic graphs; general total coloring; general vertex-distinguishing total coloring; general vertex-distinguishing total chromatic number 1000-8608(2017)03-0316-05 2016-06-15; 2017-02-23. 国家自然科学基金资助项目(61163037,61163054,11261046);宁夏回族自治区百人计划资助项目. 陈祥恩*(1965-),男,教授,E-mail:chenxe@nwnu.edu.cn;李 婷(1993-),女,硕士生,E-mail:LTKR2016@126.com. O157.5 A 10.7511/dllgxb201703015
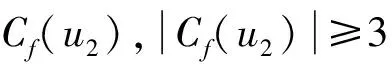
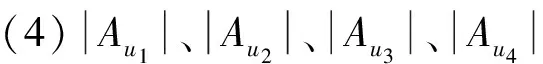
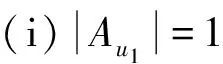
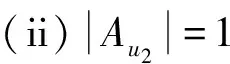
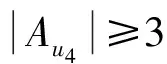
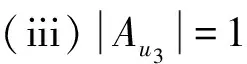
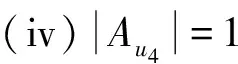

3 结 语

