基于树干不同高度直径的落叶松立木材积方程1)
韩斐斐 姜立春
(东北林业大学,哈尔滨,150040)
基于树干不同高度直径的落叶松立木材积方程1)
韩斐斐 姜立春
(东北林业大学,哈尔滨,150040)
以大兴安岭兴安落叶松为研究对象,基于树干15个不同相对高度处直径和1.3 m处胸径分别建立一元和二元材积方程。利用S-PLUS软件的广义非线性GNLS模块对各模型进行拟合。采用指数函数、幂函数和常数加幂函数对立木材积模型拟合过程中产生的异方差现象进行校正。采用确定系数(R2)、均方根误差(ERMS)、平均误差绝对值(BMA)和相对误差绝对值(BMP)4个指标对模型进行评价。结果表明,基于树干相对高度30%处直径的一元和二元模型拟合效果最好。模型检验结果表明:相对于传统的一元模型,基于相对树高30%处直径的一元模型的ERMS、BMA和BMP分别降低了25.6%、24.7%、24.7%;相对于传统的二元模型,基于相对树高30%处直径的二元模型的ERMS、BMA和BMP分别降低了55.6%、41.2%、41.2%。二元模型的检验精度明显优于相应的一元模型。
兴安落叶松;相对高度直径;异方差;材积;预测精度
立木材积方程在林业数表编制、森林资源调查、生物量和碳储量研究等方面有着广泛的应用[1-4],胸径是构建立木材积方程和生物量模型等所用的基本测树因子[5-7]。为了便于测量及减少测量误差,美国采用树高1.37 m处的直径作为胸径,日本采用树高1.2 m处的直径作为胸径,我国与世界上大部分国家采用树高1.3 m处的直径作为胸径。随着林业测树技术的发展,如高性能光学测树仪器(Criterion RD 1000)能够准确测量树干不同高度处的直径[8]。目前关于树干不同高度直径对立木材积方程精度评价的研究还鲜见报道。笔者以兴安落叶松(Larixgmelinii)为例,基于落叶松实测的树干15个相对高度的直径数据,分别拟合林业上常用的一元和二元材积方程,并与传统的基于树高1.3 m处胸径的材积模型进行对比分析。基于拟合统计量、异方差校正、模型残差图和检验统计量,选出最优材积精度模型及对应的树干相对高度,旨在为大兴安岭落叶松森林经营、提高材积估测及生长和收获的预测提供科学依据。
1 数据与方法
1.1 数据
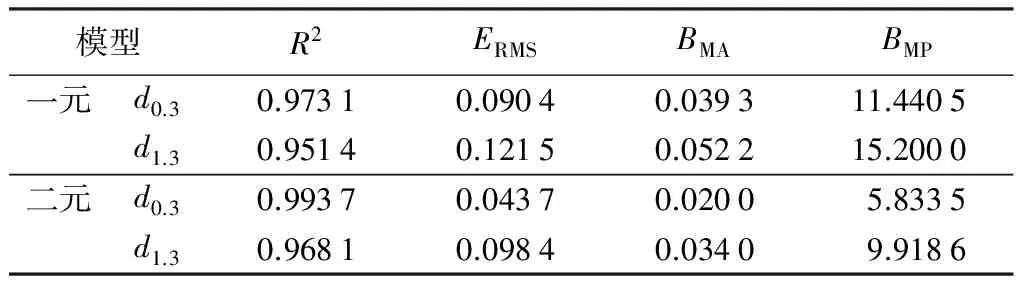
本研究所用的数据来自大兴安岭伊勒呼里山北坡西北部立地亚区的落叶松天然林样地,树木被伐倒后,测量胸径、树高及15个相对树高0、2%、4%、6%、8%、10%、15%、20%、30%、40%、50%、60%、70%、80%、90%处的直径,通过区分求积法计算立木材积。样地采集样木915株,通过绘制树高—胸径散点图剔除5株异常数据。样木以5(5 表1 样木调查因子统计量 1.2 方法 1.2.1 基础模型及异方差校正 常用的立木材积模型包括一元模型和二元模型。通常都采用以下形式[9-11]: (1) (2) 式中:V为材积;di为不同相对树高处的直径;H为树高;ε为误差项;a、b、c为方程参数。 指数函数: g(μi,α)=exp(αμi)。 (3) 幂函数: g(μi,β)=|μi|β。 (4) 常数加幂函数: g(μi,δ)=δ1+|μi|δ2。 (5) 1.2.2 模型评价及检验指标 利用S-PLUS软件对模型进行拟合得到参数估计值。拟合结果采用确定系数(R2)和均方根误差(ERMS)进行评价;检验结果通过确定系数(R2)、均方根误差(ERMS)、平均误差绝对值(BMA)和相对误差绝对值(BMP)进行检验。它们相应的数学表达式为: (6) (7) (8) (9) 2.1 模型拟合总体评价 以不同相对树高处的直径(含树高1.3 m处胸径)与树高分别建立一元和二元材积模型。利用S-PLUS软件的广义非线性GNLS模块对一元和二元各16个材积模型分别拟合。参数估计值见表2,可以看出,各模型参数变化较大。将表2中得到的参数估计值分别代入各模型中,计算各模型的统计评价指标R2和ERMS(表2)。依据R2最大和均ERMS最小的原则,选择最优模型。从16个一元模型中可以看出,基于相对树高30%处直径的一元d0.3模型R2最大,且ERMS最小。在16个二元模型中,也是基于相对树高30%处直径的二元d0.3模型R2最大,且ERMS最小。相对于传统一元d1.3模型,一元d0.3模型ERMS降低了11%;相对于传统二元d1.3模型,二元d0.3模型ERMS降低了45.2%。二元模型的拟合效果明显优于相应的一元模型。 2.2 异方差校正 a、c、e、g分别为一元d0.3、一元d1.3、二元d0.3、二元d1.3未校正模型;b、d、f、h分别为一元d0.3、一元d1.3、二元d0.3、二元d1.3校正模型。 变量a一元二元b一元二元c一元二元R2一元二元ERMS一元二元d00.00090.00011.79291.2273—1.45780.82420.86750.27690.2403d0.020.00040.00012.07931.5834—1.17060.88950.92010.21950.1867d0.040.000202.30341.8372—1.12230.92270.95650.18350.1376d0.060.000202.36821.9249—1.07270.94040.97180.16120.1110d0.080.000302.33701.9118—1.08860.94410.97770.15610.0986d0.10.000302.34501.9317—1.05420.95080.98220.14650.0880d0.150.00040.00012.31091.9003—1.08960.94850.98340.14980.0851d0.20.00040.00012.32551.9217—1.07220.95290.98660.14330.0765d0.30.00040.00012.35551.9664—1.00130.96000.98970.13200.0671d0.40.00070.00012.25281.8677—1.12190.95160.98850.14530.0710d0.50.00100.00012.18321.8042—1.16790.94200.98420.15900.0831d0.60.00230.00012.00111.6029—1.36340.90660.96450.20180.1244d0.70.00670.00021.75121.3272—1.60850.84880.93380.25670.1698d0.80.02820.00011.39550.9551—2.15140.72490.89640.34630.2126d0.90.13350.00010.97770.5766—2.63050.54230.84800.44670.2574d1.30.00040.00012.22491.8725—0.81440.94960.96560.14830.1225 表3 材积模型误差方差函数结果比较 2.3 参数估计及拟合统计量评价 表4给出了最优材积模型(d0.3)和传统模型(d1.3)基于最小二乘法和异方差校正后各模型参数估计值及拟合统计量。可以看出,模型加权后参数估计的渐进标准误差都小于未加权的参数估计的渐进标准误差,计算渐进标准误差变化率。一元模型中,d0.3模型参数a和b的渐进标准误差分别下降78%和56%,d1.3模型参数a和b的渐进标准误差分别下降76%和63%;二元模型中,d0.3模型参数a、b和c的渐进标准误差分别下降67%、31%和16%,d1.3模型参数a、b和c的渐进标准误差分别下降77%、60%和37%。相对于d1.3模型,一元和二元d0.3模型的ERMS分别下降了8%和44%。 表4 模型参数估计值及其拟合的统计量 2.4 模型检验 利用检验数据,基于表4中各模型的参数估计值,利用S-PLUS软件计算各模型的R2、ERMS、BMA和BMP。模型的R2越大、ERMS、BMA和BMP越小,精度越高。检验结果见表5。可以看出,无论是一元模型还是二元模型,d0.3模型的预测精度优于d1.3模型,且二元模型优于相应的一元模型。模型检验指标与建模数据结果基本一致。 表5 模型检验 利用大兴安岭兴安落叶松的910株样木的实测数据,对16个树干不同高度直径的一元和二元立木材积方程的拟合效果进行了对比分析。树干不同相对高度直径的立木材积方程的参数估计及拟合评价指标都存在差异,其中基于树干相对高度30%处直径的一元和二元模型拟合效果最好。树干不同高度直径的二元材积方程的拟合效果优于对应的一元材积方程。 模型检验结果表明:相对于d1.3的一元模型,基于相对树高30%处直径的一元模型的ERMS、BMA和BMP分别降低了25.6%、24.7%、24.7%;相对于d1.3的二元模型,基于相对树高30%处直径的二元模型的ERMS、BMA和BMP分别降低了55.6%、41.2%、41.2%。二元模型的检验精度明显优于相应的一元模型。 综上所述,基于树干相对高度30%处直径所建立的立木材积方程能提高单木材积的预测精度。如使用高性能光学测树器等便携仪器对不同树干高度直径进行测量时,可测量树干相对高度30%处的直径代替胸径预测立木材积。本研究没有考虑测树器测量误差的影响,建议使用本研究所构建树干相对高度30%处直径的一元和二元模型前进行误差校正。 [1] MUUKKONEN P. Generalized allometric volume and biomass equations for some tree species in Europe[J]. European Journal of Forest Research,2007,126(2):157-166. [3] YOON T K, PARK C W, SUN J L, et al. Allometric equations for estimating the aboveground volume of five common urban street tree species in Daegu, Korea[J]. Urban Forestry & Urban Greening,2013,12(3):344-349. [4] GONZALEZ-BENECKE C A, SALVADOR A, GEZAN LISA J, et al. Estimating Pinus palustris tree diameter and stem volume from tree height, crown area and stand-level parameters[J]. Journal of Forestry Research,2014,25(1):43-52. [5] 刘镜婷,姜立春.大兴安岭不同区域落叶松相容性材积方程及异方差研究[J].林业科学研究,2016,29(3):317-323. [6] 黄晓东,冯仲科,解明星,等.自动测量胸径和树高便携设备的研制与测量精度分析[J].农业工程学报,2015,31(18):92-99. [7] 曾伟生.3种异速生长方程对生物量建模的对比分析[J].中南林业调查规划,2014,33(1):1-3. [8] 张兴龙,姜立春.兴安落叶松树干去皮直径预测模型[J].林业科学研究,2015,28(1):67-73. [9] FOWLER G W. Individual tree volume equations for red pine in Michigan.[J]. Northern Journal of Applied Forestry,1997,14(2):53-58. [10] JOHNR B, HARRYV Jr W. Ecoregion-based local volume equations for appalachian hardwoods[J]. Northern Journal of Applied Forestry,2008,25(2):87-92. [11] 夏忠胜,曾伟生,朱松,等.贵州省人工杉木立木材积方程研建[J].北京林业大学学报,2012,34(1):1-5. [12] 胥辉.一种与材积相容的生物量模型[J].北京林业大学学报,1999,21(5):32-36. [13] 吴明山,胥辉,叶江霞.兴安落叶松材积模型中的异方差研究[J].山东林业科技,2010,40(2):14-17. [14] 曾鸣,聂祥永,曾伟生.中国杉木相容性立木材积和地上生物量方程[J].林业科学,2013,49(10):74-79. [15] FORTIN M, DAIGLE G, UNG C H, et al. A variance-covariance structure to take into account repeated measurements and heteroscedasticity in growth modeling[J]. European Journal of Forest Research,2007,126(4):573-585. [16] MCROBERTS R E, WESTFALL J A. Effects of uncertainty in model predictions of individual tree volume on large area volume estimates[J]. Forest Science,2014,60(1):34-42. [17] ZHANG L J, PENG C H, HUANG S M, et al. Development and evaluation of ecoregion-based jack pine height-diameter models for Ontario[J]. Forestry Chronicle,2002,78(4):530-538. [18] PENG C, ZHANG L, ZHOU X, et al. Developing and evaluating tree height-diamter models at three geographic scales for black spruce in Ontario[J]. Northern Journal of Applied Forestry,2004,21(2):83-92. [19] 曾伟生,唐守正.非线性模型对数回归的偏差校正及与加权回归的对比分析[J].林业科学研究,2011,24(2):137-143. [20] WANG M, KANE M, BORDERS B, et al. Direct variance-covariance modeling as an alternative to the traditional guide curve approach for prediction of dominant heights[J]. Forest Science,2014,60(4):652-662. [21] UZOH F C C, OLIVER W W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model[J]. Forest Ecology & Management,2008,256(3):438-445. [22] PINHEIRO J C, BATES D M. Mixed-effects models in S and S-plus[M]. New York: Springer,2000. Tree Volume Function Based on Diameter at Different Relative Heights of Dahurian Larch// Han Feifei, Jiang Lichun(Northeast Forestry University, Harbin 150040, P. R. China)// Journal of Northeast Forestry University,2017,45(4):65-69. One-variable and two-variable volume equations were established based on 15 sets of diameters at different relative height and diameter at breast height (1.3 m) forLarixgmeliniiin Daxinganling. All models were fitted using GNLS in S-PLUS. Variance functions (exponential function, power function and constant plus power function) were incorporated into generalized models to reduce heteroscedasticity. Coefficient determination (R2), root mean square error (ERMS), mean absolute bias (BMA), and mean percentage of bias (BMP) were employed to evaluate the precision of different individual volume models. The best one variable and two variable volume equations were found based on the diameter of thirty percent of relative height. By model validation, one variable model based on diameter at 30% relative height reducedERMS,BMAandBMPby 25.6%, 24.7%, and 24.7%, respectively, in comparison with traditional one-variable model. Compared with traditional two-variable model, the model based on diameter at 30% relative height reducedERMS、BMAandBMPby 55.6%, 41.2%, and 41.2%, respectively. Prediction precision of two-variable model is better than that of one-variable model. Larixgmelinii; Diameter at relative height; Heteroscedasticity; Volume; Prediction precision 1)“十二五”国家科技支撑计划项目(2012BAD22B0202)、国家自然科学基金项目(31570624)。 韩斐斐,女,1992年1月生,东北林业大学林学院,硕士研究生。E-mail:1329559697@qq.com。 姜立春,东北林业大学林学院,教授。E-mail:jlichun@nefu.edu.cn。 2016年12月7日。 S758.1 责任编辑:戴芳天。
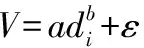

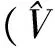



2 结果与分析
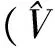




3 结论与讨论


