利用深度回归分析天津市区土体剪切波速

侯 颉， 塔 拉

(中国地震局第一监测中心，天津 300180)

利用深度回归分析天津市区土体剪切波速

侯 颉， 塔 拉

(中国地震局第一监测中心，天津 300180)

应用数理统计方法分析了天津市78个钻孔，2 212组不同岩土体的剪切波速数据，得到了其区分岩土类型和不区分岩土类型2种情况下最优的剪切波速回归公式，利用所得经验公式对实际钻孔不同深度剪切波速进行了预测，并基于实测结果对预测结果进行了分析。结果表明，天津市区主要岩土类型剪切波速与深度的相关性大小存在较为明显的差异，其中粘土、粉土和粉质粘土的相关性最好，粉砂和细砂次之，人工填土最差；各类主要岩土体剪切波速与埋深之间的相关关系中多项式模型拟合精度最高，给出的各类主要土体剪切波速与埋深经验关系准确可靠，可用于天津市区主要土体剪切波速计算工作。

剪切波速；回归分析；土层深度；土体类型

0 引言

剪切波速是工程场地地震安全性评价和地震小区划的重要指标[1-2]，能反映地基土的强度、变形特性，可用于场地土抗震类型和场地类别的确定、饱和砂土和粉土的液化判别以及地下管道的抗震设计，并在土动剪切模量G、卓越周期Tp以及浅基础的抗压、抗剪、抗弯(摇摆)和抗扭刚度等参数的计算等方面有广泛的应用[3-7]。剪切波速一般由现场实测结果获得，然而在实际工作中，由于城市同一区域密集的工程建设需要重复多次进行场地剪切波速测试，势必会影响工程进度，加大工程投资，造成巨大浪费。因此，若能对该区域已有的钻孔资料进行统计分析，给出其各种岩土类型剪切波速随深度变化的合理有效的经验关系，将有利于节约成本，产生良好的社会和经济效益[2，8]。

一般情况下，同一类型的土体在一定范围内，土层深度越深，土的密实程度越大，剪切波速也越大。国内学者在土层深度方面进行了广泛的研究，已初步得到了我国太原、深圳、南京、合肥、上海、昆明、泉州、西安、东营、邯郸、大连、衡水和天水等多个省市地区不同岩土类型剪切波速随深度的变化规律及二者间的关系[1-4，8-20]。然而剪切波速与深度的关系还会受到地层结构、土的赋存环境和土风化程度等因素的影响。本文探讨了天津市区多种主要岩土体剪切波速随深度的变化关系，并给出了其有效的估算经验公式，供天津市实际建筑工程参考使用。

1 地质背景及资料来源

天津地区除蓟县山区外，90%以上的面积为平原区，区内地势平坦，地形自然坡度仅为1/3 000～1/4 000，地面高程为3.0～3.5 m，地下水埋深一般为2.4～3.5 m。地表被广泛的第四纪陆相沉积覆盖，滨海地带主要为潮汐与河流频繁作用的交互沉积区，而市区部分为河流冲击、海积、湖积作用的交互堆积区。其中，蓟县山区和北部平原区面积较小，第四纪沉积物厚度较浅，以陆相冲积物、洪积物为主，岩相变化快；而南部平原区第四纪沉积物厚度大，以冲击、湖积和海积为主，层位稳定，分布广泛[21]。

本文的数据资料全部来源于中国地震局第一监测中心近年来在天津市区进行的大量工程场地地震安全性评价工作中的钻孔剪切波速资料，均采用单孔波速测试方法获得。本文资料包括78个钻孔剪切波速的测试结果，共2 212组不同场地不同土体类型的剪切波速数据，主要分布于天津南部平原地区，全面反映了天津市区(即外环以内区域)的地层情况。

目前，国内外相关研究已证明剪切波速测试误差是客观存在的，但这些研究尚无法给出剪切波速误差的概率分布，以及其与岩土类型、土层深度等因素之间的关系[22]。因此，本文根据单孔法简单易行、成本低、数据处理方便，但同时具有波形受外界干扰较大，有时需要工程人员依据经验处理数据的特点，规定测试场地尽可能选取环境噪音较小、平整无障碍物、无植被覆盖、表层无杂填土的场地；并要求测试人员不仅提供测试结果，还需提供波形结果以供验证，保证剪切波速数据的准确性。

2 统计分析

本文所统计的资料包含的岩土类型有人工填土、粉质砂土、淤泥、淤泥质粘土、粉质粘土、粉土夹粉砂、粉土、粘质粉土、粘土、粉砂和细砂，各孔全部覆盖层均小于7 m，土体样本深度主要分布于0～120 m的范围内，密度范围约为1.69～2.22 g/cm3，剪切波速主要分布于98～625 m/s的范围内。

表1 天津市区岩土类型统计样本数量和深度范围

本研究区内，土体类型以粉质粘土、粉土、粉砂、粘土、人工填土和细砂为主，其他类型(粉质砂土、淤泥等)的剪切波速数据仅有数例(图1)，由此认为粉质粘土、粉土、粉砂、粘土、人工填土和细砂这6种土体类型，在一定程度上可以代表天津市区100 m以内的所有土体类型。又由于从统计学角度来看，利用个别或少量样本对某种土体类型的剪切波速进行统计回归势必不够准确，因此本文将仅针对粉质粘土、粉土、粉砂、粘土、人工填土和细砂这6种主要土体类型开展剪切波速的回归研究工作。

图1 天津市区各岩土类型样本数量分布图

3 剪切波速回归分析

各类土体剪切波速与深度具有显著的相关性。通常，场地土剪切波速VS与土层深度H之间的经验关系主要采用线性模型(式(1))、一元二次多项式模型(式(2))和指数模型(式(3))进行表示[8，19-20]。

VS=aH+b

(1)

VS=aH2+bH+c

(2)

VS=cHd

(3)

式(1)～(3)中，VS为剪切波速；H为土体深度；a、b、c、d为待定系数。

3.1 不分岩土类型分析

在不分岩土类型的情况下，将研究区内所有78个钻孔的2 212组测试数据汇总，发现所有岩土体剪切波速随土层深度的增加宏观上呈现出递增趋势(图2)。应用上述3种模型分别对全部钻孔测试数据进行剪切波速VS与土层深度H关系回归分析，拟合参数列于表2。通过分析表2可知，3种模型的拟合度R2均大于0.8，且其中多项式模型的拟合度R2最高，说明多项式模型更适合描述天津市区土体的剪切波速与深度间的关系。

图2 所有岩土类型的剪切波速与土层深度关系散点图

模型abcdR2线性模型3.8314133.530.8894多项式模型0.02005.7241104.800.9062指数模型150.130.01400.8454

3.2 分岩土类型分析

考虑岩土类型对工程场地土层剪切波速VS与土层深度H关系的影响，将天津市区粉质粘土、粉土、粉砂、粘土、人工填土和细砂6种主要岩土类型的剪切波速与土层深度的关系进行整理(图3)。由

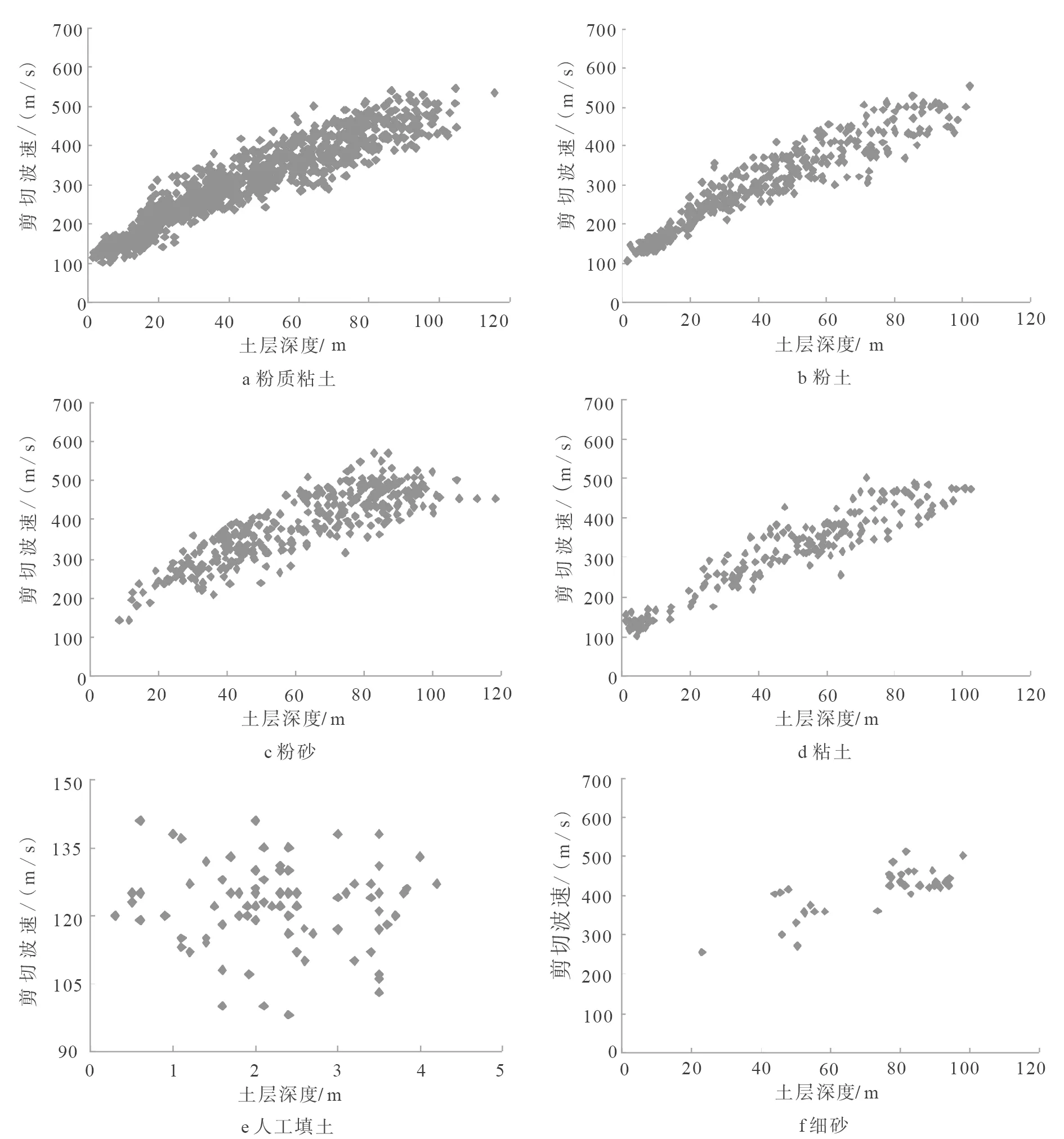
图3 不同土类的剪切波速与土层深度关系散点图

图3可以看出，粉质粘土、粉土、粉砂、粘土和细砂5种主要岩土类型的剪切波速与深度间存在明显的相关关系，但人工填土未表现出剪切波速与深度间的相关性。分析其原因认为，人工填土的物质成分较为复杂，一般由碎石、沙土、粘性土等组成，其均匀性和压实性均较差，导致其波速与深度间无明显相关关系，因此本文将不对其进行回归分析。

分别采用线性、多项式和指数模型对各岩土类型进行剪切波速与土层深度关系的回归分析，经验关系的拟合参数见表3。比较表3中3种模型下不同岩土类型的拟合精度可以得出，粉质粘土、粉土、粉砂、粘土和细砂5种主要岩土类型在多项式模型下拟合精度(R2)最大，拟合效果最佳。其中粘土在3种模型下R2均高于其他岩土类型，表明粘土的剪切波速和深度之间具有很好的相关性。分析各岩土类型的线性模型经验公式发现，同等深度条件下，由粘土到细砂粒径逐渐增大，其相应的剪切波速也逐渐增大。将表2和表3多项式模型的拟合精度进行比较后发现，不分岩土类别与分岩土类别结果差别并不十分明显，仅粘土和粉土的区分岩土类别拟合精度有所提高，因此本文认为不分岩土类型的拟合公式精度即可基本满足一般的工程服务需要。

表3 天津市区主要岩土类型回归模型参数及拟合精度

4 工程应用及效果分析

为了验证以上天津市区主要剪切波速与深度关系回归分析的可靠性，将本文回归模型的经验公式应用于实际钻孔，并将预测结果与钻孔实测数据进行对比研究。本文选取天津市区内某深度为100 m的钻孔TJ-23，分别使用不区分岩土类型的多项式模型(表2)与区分岩土类型的多项式模型(表3)对其剪切波速进行预测，预测结果及其相对误差见表4。

表4 TJ-23孔剪切波速与土层深度关系的预测结果与实测结果比较

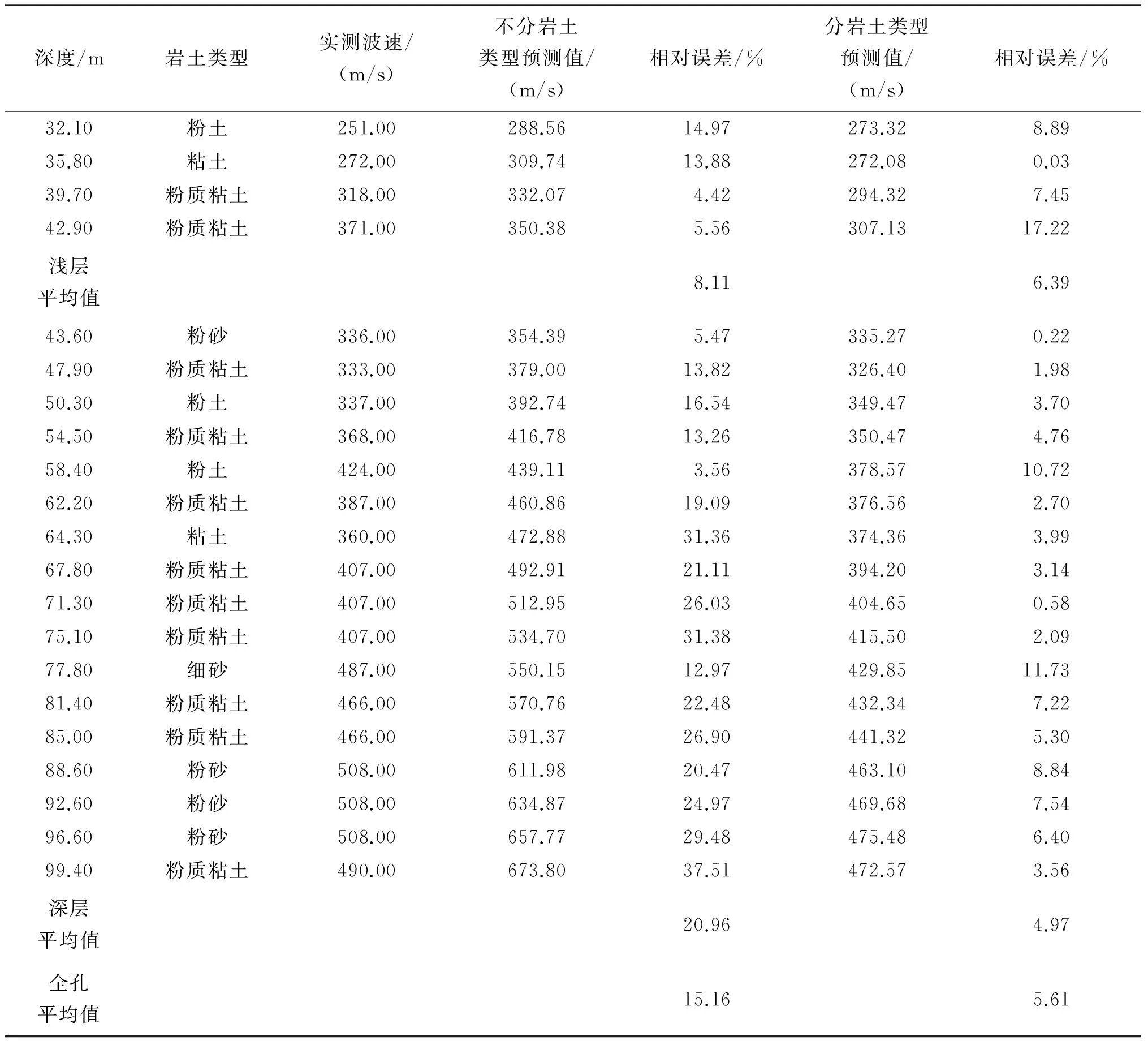
续表

由表4可以看出，总体上区分岩土类型对剪切波速进行估算的相对误差平均值约为5.61%，小于在不区分岩土类型的条件下剪切波速估算值的相对误差平均值(约15.16%)；对于浅部地层(约45 m以内深度)，区分岩土类型的相对误差平均值(约6.39%)与不区分岩土类型的相对误差平均值(约8.11%)相差不大，甚至在多个深度段区分岩土类型的拟合效果更差；对于深部地层(约45～100 m深度)，区分岩土类型的相对误差平均值(约4.97%)明显小于不区分岩土类型的相对误差平均值(约20.96%)。分析结果认为，随着深度的增加，土壤压实程度逐渐增强，其波速成分与岩土类型的关系也更紧密，从而使在深部地层应用区分岩土类型的拟合公式对剪切波速进行估算的结果会更加准确。因此，在深部且岩土类型已知的地层，建议选用表3中区分岩土类型的多项式模型进行计算，而对于浅部或岩土类型未知的地层，建议使用表2中不区分岩土类型的多项式模型(式4)进行估算，

VS=0.0200H2+5.724 1H+104.80

(4)

5 结论

1)不同岩土类型的剪切波速与其对应深度的相关性大小存在较为明显的差异，其中粘土、粉土和粉质粘土的相关性最好，粉砂和细砂次之，人工填土最差。

2)应用大量钻孔剪切波速实测数据，回归分析天津市区剪切波速与深度之间的关系，给出了区分岩土类型和不区分岩土类型2种条件下天津市区主要土类剪切波速与深度的统计公式。结果表明，天津市区主要土类剪切波速与深度具有显著的相关性，且其中多项式模型的拟合精度最高。

3)本文建立的回归模型可供天津市区主要土类剪切波速预测工作使用，但不适用于人工填土。实际应用中，在深部且岩土类型已知的地层，建议选用区分岩土类型的多项式模型进行计算，而对于浅部或岩土类型未知的地层，建议使用不区分岩土类型的多项式模型进行估算。

4)本文仅利用深度和岩土类型2种数据，对天津市区几种不同类型的土体剪切波速进行了简单的统计分析。虽然能够得到一个综合的经验关系公式，但是该经验公式可能在其他一些区域并不适用。因此，未来研究需进一步综合考虑土体的含水量和所处的环境、围压等因素，针对不同环境的土层进行独立的分析，从而得到更加准确的评价结果。

[1] 安卫平, 兰青龙, 贺明华, 等. 太原地区剪切波速的深度分布[J]. 山西地震, 1997(1/2): 88-94.

[2] 张小平, 马顺, 金源, 等. 大连地区工程场地各类岩土剪切波速的变化特征分析[J]. 防灾减灾学报, 2012, 28(4): 7-11.

[3] 程祖锋, 李萍, 李燕, 等. 深圳地区部分岩土类型剪切波速与深度的关系分析[J]. 工程地质学报, 1997, 5(2): 163-168.

[4] 陈国兴, 徐建龙, 袁灿勤. 南京城区岩土体剪切波速与土层深度的关系[J]. 南京建筑工程学院学报, 1998(2): 32-37.

[5] 高印立, 阎澍旺, 王金英. 剪切波速与土性指标间的统计关系[J]. 建筑科学, 1998, 14(5): 20-22.

[6] 蔡力挺, 韩玉庆. 波速测试技术在岩土工程勘察中的应用[J]. 西部探矿工程, 2009(3): 32-37.

[7] 郭明珠, 贾连军, 铁瑞, 等. 剪切波速测试方法的现状分析[J]. 西北地震学报, 2011, 33(S): 21-23.

[8] 何仲太, 马保起, 卢海峰. 衡水市岩土体剪切波速与土层深度的关系[J]. 科学技术与工程, 2014, 14(35): 90-96.

[9] 周锡元, 王广军, 苏经宇. 场地·地基·设计地震[M]. 北京: 地震出版社, 1990: 30-60.

[10] 高玉峰, 刘汉龙. 合肥膨胀土剪切波速的特征分析[J]. 岩土工程学报, 2003, 25(3): 371-373.

[11] 高飞, 孙小刚. 上海地区场地剪切波速的特征分析[J]. 上海地质, 2005(2): 27-29, 36.

[12] 李存志, 李向新, 姚明波, 等. 昆明盆地剪切波速与地基特性相关分析研究[J]. 昆明冶金高等专科学校学报, 2006, 22(3): 1-5, 10.

[13] 齐文浩, 刘德东, 张宇东, 等. 剪切波速推测的工程应用[J]. 防灾科技学院学报, 2007, 9(4): 17-20.

[14] 齐文浩, 刘德东, 兰景岩, 等. 西安阎良区土层剪切波速统计分析[J]. 防灾科技学院学报, 2008, 10(4): 10-12.

[15] 徐国栋, 马东辉, 吴共湖, 等. 泉州市规划区场地抗震性能与土地适宜性分区研究[J]. 世界地震工程, 2007, 23(4): 153-162.

[16] 齐静静. 山东东营城区剪切波速回归分析及应用[J]. 勘查科学技术, 2011(2): 23-26.

[17] 王帮圆, 李世峰, 王帮团, 等. 邯郸市区场地土剪切波速与埋深相关性分析[J]. 河北工程大学学报: 自然科学版, 2013, 30(3): 92-95.

[18] 王强, 王兰民, 吴志坚, 等. 天水市岩土体剪切波速与埋深的变化关系[J]. 地震工程与工程振动, 2014, 34(S): 247-252.

[19] 陶小三, 杨伟林, 高志兵, 等. 南京河西地区岩土体剪切波速与土层深度的关系[J]. 防灾减灾工程学报, 2009, 29(3): 320-324.

[20] 刘红帅, 郑桐, 齐文浩, 等. 常规土类剪切波速与埋深的关系分析[J]. 岩土工程学报, 2010, 32(7): 1142-1149.

[21] 陈宇坤, 赵国敏, 闫成国, 等. 天津市活动断层探测与地震危险性评价[M]. 北京: 科学出版社, 2013: 48-50.

[22] 陈卓识. 现场剪切波速测试误差及其对地震动影响研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2015: 1-13.

Depth Regression Analysis of Soil Shear Wave Velocity in Tianjin Urban Region

HOU Jie, TA La

(The First Monitoring Center, China Earthquake Administration, Tianjin 300180, China)

The shear wave velocity data of 2 212 sets of different soils of 78 drilling wells in Tianjin urban region were analyzed using mathematical statistics method. The optimal regression formulas of shear wave velocity were obtained in the case of considering and ignoring soil types. Then the empirical formulas were used to estimate the shear wave velocity of different depths in the actual drilling, and the estimated results were analyzed basing on the measured results. The results show that, an obvious difference between the correlation of shear wave velocity and soil depth of main soil types are existed in Tianjin urban region, in which the correlations of clay, silt and silty clay are the best, followed by siltstone and fine sandstone, and artificial filled are the worst; the fitting accuracy of polynomial models are the highest in all relationships between shear wave velocity and soil depth of main soil types; the given empirical relationships of shear wave velocity and soil depth of different main soil types are accurate and reliable, and they can be used to calculate the shear wave velocity of main soil types in Tianjin region.

shear wave velocity; regression analysis; soil depth; soil type

2016-12-12

中国地震局第一监测中心主任基金(FMC2016002)

侯颉(1989—)，女，天津人，助理工程师，主要从事综合地球物理学研究．E-mail：jiejie198907@126.com

P315.9

A

1003-1375(2017)02-0048-06

10.3969/j.issn.1003-1375.2017.02.008

侯颉，塔拉.利用深度回归分析天津市区土体剪切波速[J]．华北地震科学，2017，35(2):48-53.