考虑损失厌恶和退货因素的双渠道定价策略

段永瑞， 代祥艳

(同济大学 经济与管理学院， 上海 200092)

考虑损失厌恶和退货因素的双渠道定价策略

段永瑞*， 代祥艳

(同济大学 经济与管理学院， 上海 200092)

该研究了双渠道统一定价和双渠道差别定价问题.考虑了线下渠道的服务水平、线上渠道的退货因素以及消费者的损失厌恶有限理性行为对产品定价策略的影响，得到了不同策略下的最优价格、最优利润和最优服务水平，并分析了退货率对线上渠道价格和需求的影响.最后数值算例表明，在零售商市场份额较高时，制造商应采取双渠道统一定价策略，零售商市场份额较低时，制造商应不开通线上渠道；在双渠道统一定价和差别定价中制造商和零售商的利润均随着退货率的增大而减小；在双渠道差别定价中，制造商和零售商的利润随着损失厌恶程度的增大而增大，而线上与线下的最优价格差随着损失厌恶程度的增大而减小.

损失厌恶； 退货； 双渠道定价

随着互联网的发展，消费者购物行为发生了极大的变化，消费者足不出户就可以通过线上渠道购买到商品.为了满足消费者新的需求，越来越多的制造商开始采用线上渠道向消费者出售商品，因此，双渠道的优化问题引起了很多学者的关注.

线下渠道为提高自己的竞争力，往往会提供增值服务，如顾客去实体店买衣服，服务员可根据其身形着装推荐符合顾客品味的衣服，而线上渠道通常不能提供这类增值服务.近些年，很多研究将销售商品时所提供的服务水平考虑到双渠道定价问题中.YAN等[1]在研究双渠道定价问题时，考虑了线下渠道提供的增值服务，假设线下渠道提供的增值服务对线上需求起负向作用，对线下渠道的需求起正向作用.并研究了线上渠道的最优价格和线下渠道服务水平的关系，结果表明两者不存在确定的关系.TSAY和AGRAWAL[2]考虑了由单一制造商和两个零售商组成的供应链系统，两条零售渠道间不仅存在价格竞争，还存在服务水平竞争.并分析了两条零售渠道合作和不合作情况下的价格和服务水平的选择.罗美玲等[3]从消费者效用角度出发，研究制造商在通过传统渠道零售商分销其产品的同时，引入自营的增值服务渠道对供应链中各个参与主体的定价、市场份额和利润的影响，以及制造商愿意引入增值服务渠道的条件.研究结果表明，引入增值服务可以减轻价格双重边际效应，有效地扩大整个市场需求.刘咏梅等[4]研究了考虑服务和退货的双渠道供应链定价问题.研究发现零售服务有助于提高零售商的渠道权力，并始终使制造商获益，但只有当服务水平小于某一临界值时，才使制造商和零售商同时得到帕累托改进.吴晓志等[5]研究了考虑服务竞争的O2O供应链决策，设计了两部定价契约协调需求和服务替代系数同时扰动下的O2O供应链.研究表明，两部定价契约可以协调零售商O2O供应链，当突变范围较大时，作为博弈主导方的零售商将放弃加价销售，转向收取固定的转移支付.

由于在线上渠道购买产品时，顾客在交易结束前接触不到实体商品，有时会出现诸如尺码不对、与网上图片有色差、或者质量不过关等情况，因此线上零售渠道通常允许顾客在一定条件下退货，并得到全部或部分退款.允许顾客退货虽然在一定程度上提高了服务质量和增加了需求，但是同时也给企业的运营管理带来了一定的问题，提高了企业的运营成本.因此，如何在提供退货服务的同时能够不影响企业的利润，并把顾客退货因素考虑到定价策略中是在线零售企业急需解决的问题.目前定价问题中考虑退货因素的研究相对较少，SHULMAN等[6]研究了两家具有竞争性公司的产品定价和退货费决策问题.文章指出，退货费不仅在激烈的竞争环境中存在，但消费者不清楚产品是否符合他们的喜好时，退货费会更加严重.结果表明，相比垄断市场，竞争市场下的均衡退货费用更高.FLAPPER等[7]研究了在不完全的顾客退货信息下的生产-库存控制，需求和退货的发生遵循独立的泊松过程，同时考虑缺货和延时交货情况.运用马尔科夫决策理论，文章给出了最优的生产策略.但上述研究均未考虑退货策略对在线零售企业运作的影响.ANDERSON等[8]探究了需求量和退货量之间的关系，研究表明，需求和顾客退货之间的关系是库存计划模型中一个重要的输入变量，对两者关系的低估会急剧地增加库存管理成本.MOSTARD和TEUNTER[9]研究了考虑退货因素的报童问题.假设在一定时间内，允许顾客退货并且给予全额退款，退回的商品不影响二次销售.考虑到产品需求分配、退货概率、相关成本和收入等因素，文章给出了最佳的订货策略.姚忠[10]研究了风险约束下退货合同对供应链的协调性影响.零售商在风险约束下，分析了退货策略对单周期供应链的协调性，首先运用报童库存模型建立了供应链决策模型，然后运用解析法对满足零售商下游风险约束下的零售商决策进行了优化分析.研究表明，在风险约束制约下，零售商和供应商的期望利润都有所减少，退货合同的协调性较无风险约束情况下较弱.YAO等[11]分析了在单产品供应链系统中，价格敏感因素对退货的影响.数值结果表明，退货策略的确提高了供应链绩效，然而在价格敏感和可变需求下，不同的供应链合作伙伴从退货策略中获得的利润是不同的.陈菊红等[12]研究了退货契约在供应链协调中的作用，通过建立基于契约的供应链协调模型，得出对三级供应链实行退货契约不仅增加供应链总利润，而且协调好退货价与批发价可以达到多赢.

NASIRY[13]研究了考虑参照效应的动态定价问题，假设参照价格是历史最低价格和最近价格的加权均值，消费者是损失厌恶的.研究结果表明，损失厌恶因素限制了不同价格下的利益，大力度的折扣对公司最优价格和最优利润的不利影响可能比以前的模型预测更持久.柳键等[14]研究了考虑缺货损失情形下损失厌恶零售商的订货决策.研究结果表明，订货量随着单位残值、单位缺货损失的增大而增大;但随着损失厌恶系数、零售价格、采购价格的增大，订货量可能增大，也可能减小，这表明损失厌恶会对订货决策产生重要影响.王虹等[15]研究了损失厌恶型的零售商参与的供应链协调机制.结果表明，零售商由于害怕损失会做出偏离系统最优的决策，引入奖励—惩罚契约，通过供应商的激励可以实现供应链在回购契约下的协调.最后通过算例分析，验证了奖励-惩罚契约在供应链协调中的有效性，并说明零售商风险规避度越大，供应商为实现供应链协调付出的成本就越大.但目前很少有学者在研究双渠道定价问题时，考虑消费者损失厌恶行为.GAN等[16]在研究渠道定价问题时，假设制造商是损失中性型的，零售商是损失厌恶型的.利用前人提出的供应链合作概念，设计了风险共享机制，为下游的零售商和分销商提供了利润保护，从而实现了渠道协调.

1问题描述

考虑由单一制造商和单一零售商组成的两级供应链系统销售单一产品，产品的销售渠道分为传统的线下渠道和线上渠道.假设线上渠道允许顾客退货，并给与全额退款.参照张霖霖等[17]的研究，假设退货量与市场需求成正比，即R=θD，其中θ为退货率，D为需求量，R为退货量.

同时，为提高自己的竞争力，零售商在线下渠道提供增值服务，设线下渠道的服务水平为v∈[0，vmax]，其中，vmax为零售商能提供的最大服务水平.c(v)为线下渠道给单位产品提供水平为v的增值服务所需要的成本，参照薛顺利等[18]的研究，假设c(v)=ηv2/2.本文中假设顾客是损失厌恶型.考虑退货时的双渠道销售系统图如图1所示.

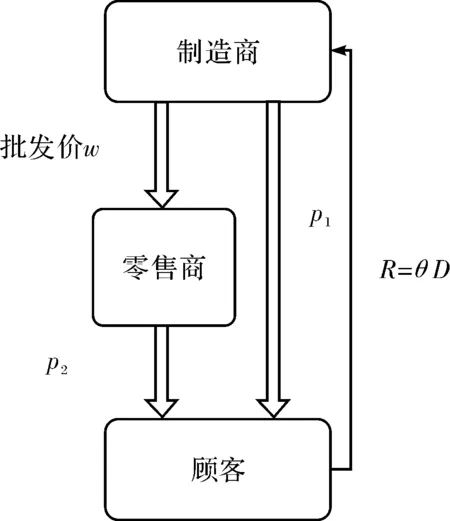
图1 考虑退货时的双渠道销售系统图Fig.1 The distribution system of dual channel considering returns

本文涉及的符号含义如下：

p1：线上渠道的产品销售价格；

p2：线下渠道的产品销售价格；

w：零售商的产品批发价格；

R：线上渠道的退货量；

θ：退货率；

c1：退货单位产品给制造商带来的损失；

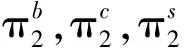
线上渠道的需求函数为：

d1=[ρa-bp1+λ1(p2-p1)]，

(1)

线下渠道的需求函数为：

d2=[(1-ρ)a-bp2+λ2(p1-p2)+gv]，

(2)

式中，ρ和 1-ρ分别表示消费者对线上渠道和线下渠道的接受程度，0<ρ<1，a表示产品的价格和服务水平均为0时的市场规模，b表示本渠道价格对需求的影响因子，g表示单位服务水平对需求的影响，λi为替代渠道的交叉价格影响因子.假设p1≤p2，且消费者厌恶损失，因此λ1≤λ2.

线下渠道和线上渠道的需求满足非负约束，即d1≥0，d2≥0，此外，线上渠道的销售价格p1，线下渠道的销售价格p2，批发价格w和成本c满足：c≤p1，c≤w≤p2.

2建模和分析

下面分别探讨几种定价策略，并对各个影响因素进行分析.首先给出基本定价策略，在此基础上研究制造商实施双渠道时采取的统一定价和差别定价策略.下述性质1～7证明过程见附录(92页).

2.1基本定价策略

假设制造商为了减少风险，只采用传统渠道销售该产品，参照徐峰等[19]的研究，传统渠道的需求函数为d=d1+d2=a-2bp+gv.假设制造商处于供应链中的主导地位，决策目标是使各自的利益最大化，运用Stackelberg博弈分析双方的最优定价策略，决策顺序为：制造商先确定批发价格，零售商在已知的批发价格基础上确定零售价格.

制造商的利润函数为

(3)

零售商的利润函数为

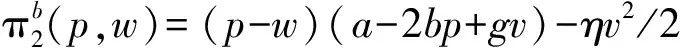
(4)

零售商的最优利润为

性质2在单渠道定价策略下，零售商提供的最优服务水平为：

由于零售商最优利润函数是关于服务水平v的二次函数，因此零售商应提供的的最优服务水平v*=v0.

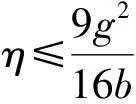
此时，零售商应提供的的最优服务水平v*=0.

2.2双渠道统一定价策略

本节将研究同时存在线上和线下渠道时的定价问题.实际中，为了减少线下渠道和线上渠道的冲突，制造商实施线上线下同价策略，如百丽、Zara等的定价模式.假设制造商保持线上渠道价格与线下渠道价格一致，并据此确定产品的批发价格w，零售商则在此基础上确定零售价格p，可得零售商利润函数为

(5)

制造商的利润函数为

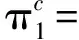
(6)

性质3当制造商采取统一定价渠道模式时，制造商确定的最优批发价格为

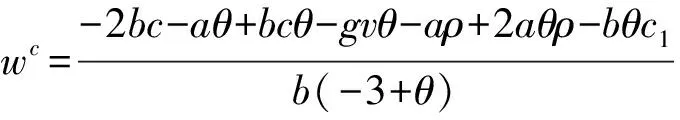
零售商确定的最优零售价格为

线上渠道的需求量为

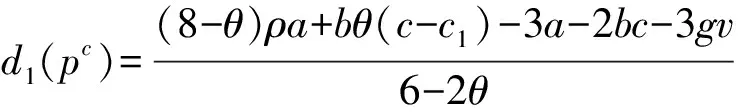
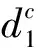
性质5在双渠道统一定价模式下，

1)零售商的最优利润为

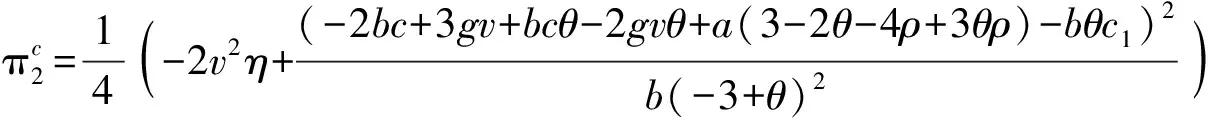
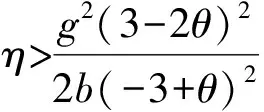
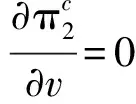
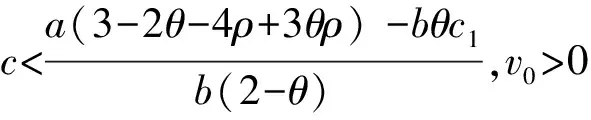
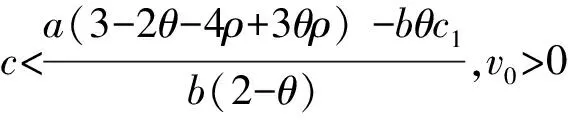
2.3双渠道差别定价策略

假设制造商处于供应链中的主导地位，线上和线下渠道采用不同的价格，仍然运用Stackelberg博弈分析双方的最优定价策略.假设批发价格w0是已知的(Yao D Q等[1])，制造商先确定线上渠道销售价格，然后零售商确定其线下零售价格.

零售商的利润函数为

(7)

制造商的利润函数为

(w0-c)((1-ρ)a-bp2+λ2(p1-p2)+gv)-

c1θ(ρa-bp1+λ1(p2-p1)).

(8)

性质6在双渠道差别定价模式下，线上渠道和线下渠道最优价格分别为

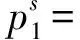
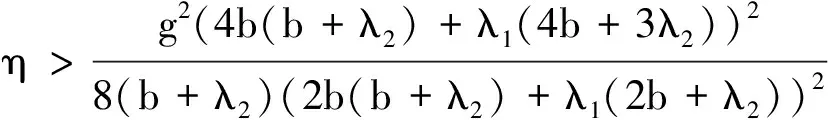
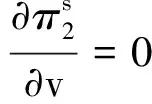
λ1(4b+3λ2))(λ1(4b(-1+θ)(bw0+a(-1+ρ))+((-1+θ)(-2bc+5bw0+3a(-1+ρ))+2bθc1)λ2+

(b+λ2)(4b(-1+θ)(bw0+a(-1+ρ))+

2(-(-1+θ)(bc-2bw0+ρa)+bθc1)λ2+

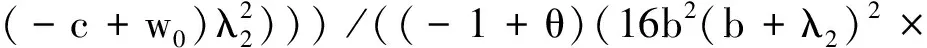
若M>0，v0<0，则零售商应提供的最优零售商水平为v*=0.

若M≤0，v0≥0，则零售商应提供的最优零售商水平为v*=v0.其中，

M=-λ1(4b(-1+θ)(bw+a(-1+ρ))+((-1+θ)(-2bc+5bw+3a(-1+ρ))+2bθc1)λ2+

(b+λ2)(4b(-1+θ)(bw+a(-1+ρ))+

2(-(-1+θ)(bc-2bw+ρa)+bθc1)λ2+

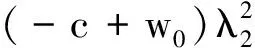
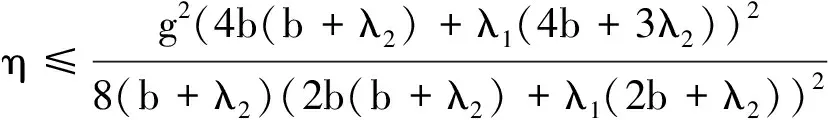
若M>0，v0<0，则零售商应提供的最优零售商水平为v*=vmax.

若M≤0，v0≥0，则零售商应提供的最优零售商水平为v*=0或v*=vmax．

3算例

本节通过算例比较分析不同策略下各参数对制造商和零售商利润的影响.

3.1零售商市场份额的影响

参数设置如下：a=1000，b=0.5，g=0.01，v=1，θ=0.1，η=1，λ1=0.02，λ2=0.03，c=50，c1=10，w0=80.

当零售商市场份额1-ρ在区间[0.2，0.7]上对各策略下制造商和零售商利润的影响，如图2和图3所示.

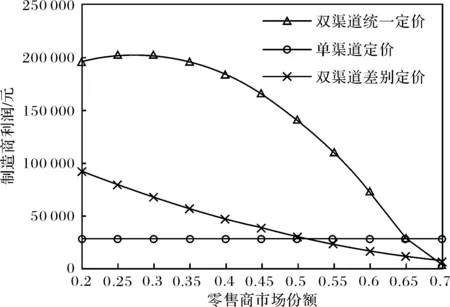
图2 各策略下制造商利润随零售商市场份额的变化Fig.2 Variation of manufacturer profits with retailer market share

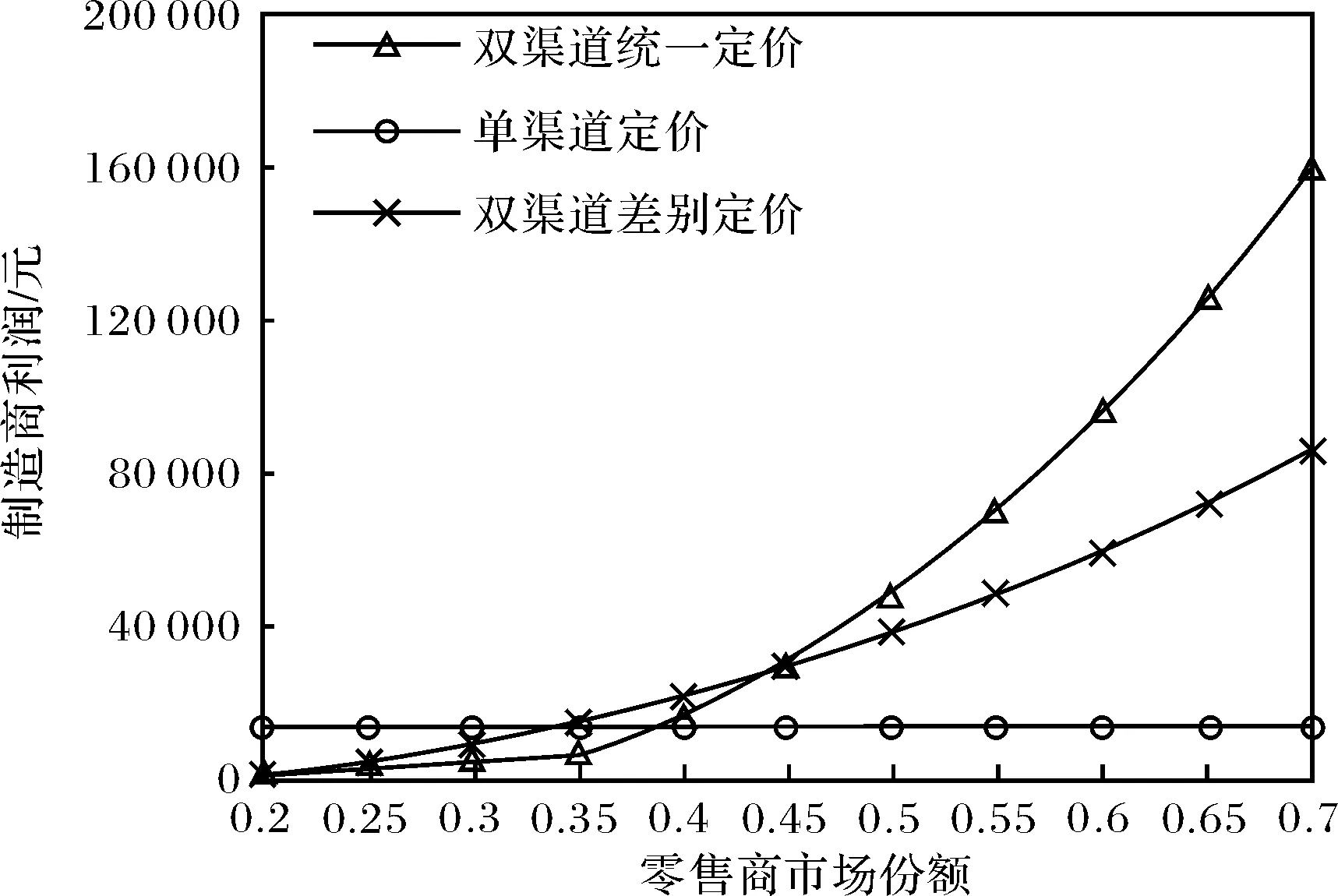
图3 各策略下零售商利润随零售商市场份额的变化Fig.3 Variation of retailer’s profits with retailer market share

图2中，在双渠道统一定价模式和差别定价模式下，制造商利润均随着零售商市场份额的增加而减少.因仅存在线下销售渠道，单渠道定价策略下制造商利润不变.当零售商市场份额较小时，双渠道统一定价模式下的制造商利润最大；当零售商市场份额较大时， 单渠道定价策略下的制造商利润最大.对于制造商来说，在其它参数不变的情况下，选择何种策略要根据线上渠道或线下渠道的市场份额而定.

图3中，双渠道统一定价模式和差别定价模式下零售商利润均随着零售商市场份额的增加而增加，单渠道定价策略下零售商利润不变.当零售商市场份额足够大时，双渠道统一定价模式下的零售商利润最大，单渠道定价策略下的零售商利润最小.

3.2退货率影响分析

假设线上渠道零售份额ρ=0.4，保持其他参数不变，分析各策略下制造商利润随退货率变化的情况.

从图4中可以看出，双渠道统一定价模式和双渠道差别定价模式下的制造商利润随着退货率的增加而减少，且双渠道统一定价策略下的制造商利润最大.因此，在这种情形下，制造商应选择双渠道统一定价模式.

从图5中可以看出，双渠道统一定价策略下，零售商利润随着退货率的增大而减少，而双渠道差别定价策略下，零售商利润几乎不变.在此情况下，双渠道统一定价策略下的零售商利润最大.

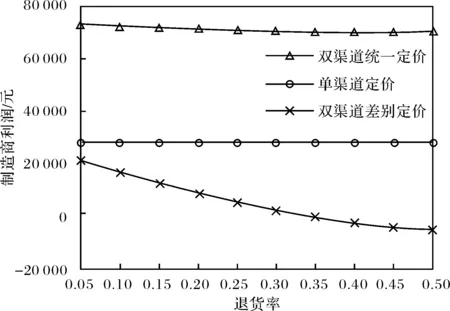
图4 各策略下制造商利润随退货率的变化Fig.4 Variation of manufacturer’s profits with the return rate

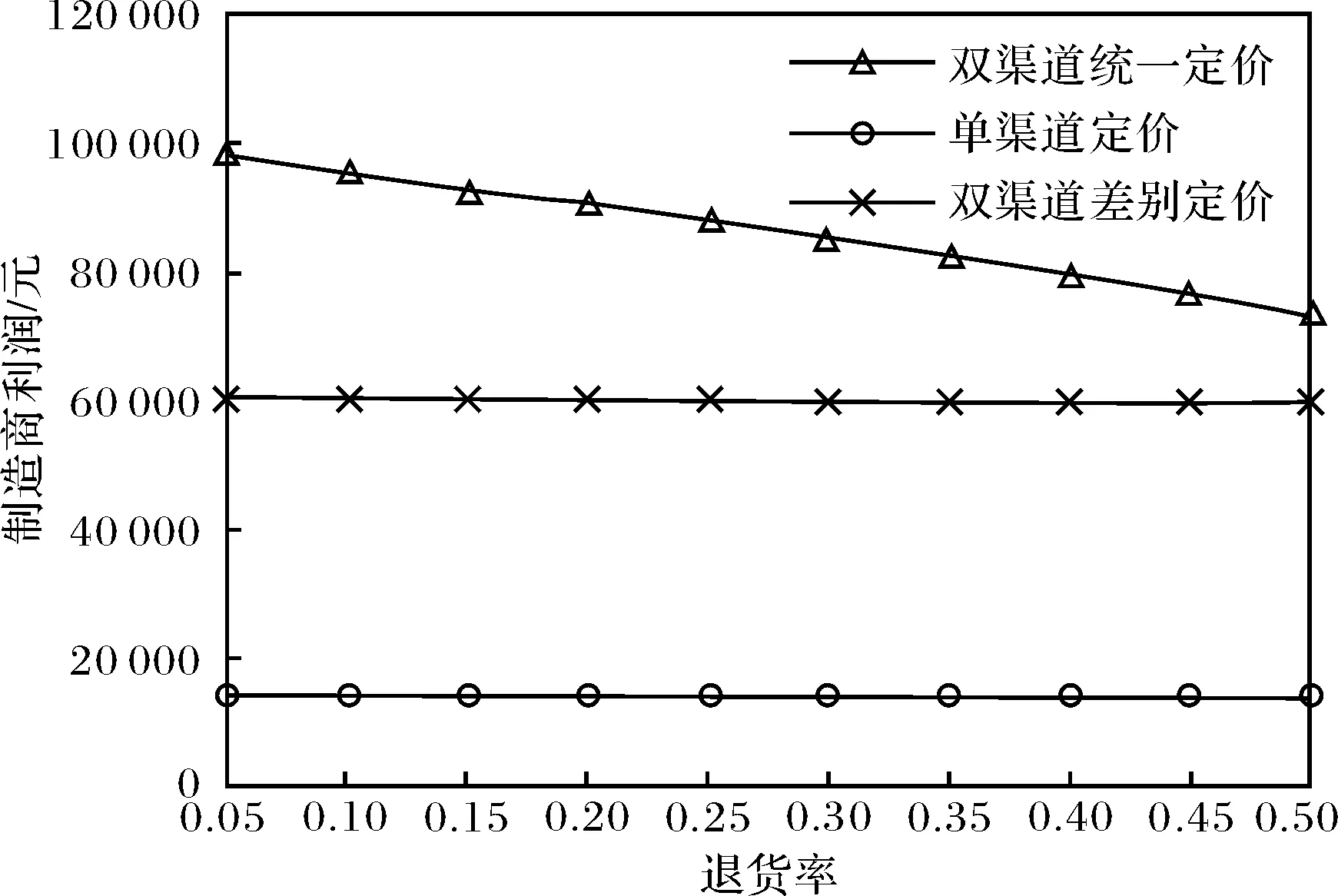
图5 各策略下零售商利润随退货率的变化Fig.5 Variation of retailer’s profits with the return rate

3.3服务水平影响分析

假设线上渠道零售份额ρ=0.4，退货率θ=0.1，保持其他参数不变，本节分析各策略下的零售商利润随服务水平的变化情况.

从图6～图8可以看出，各策略下的零售商利润先随着服务水平的增加而增加，当服务水平大于临界值后，零售商利润随着服务水平的增加而减少.在其他参数不变的前提下，在双渠道统一定价模式、单渠道定价模式、双渠道差别定价模式下，使得零售商利润最大的服务水平分别为4、2、2.

3.4损失厌恶影响因子分析

由于在单渠道定价和双渠道统一定价模式中不含有损失厌恶因子，因此仅对双渠道差别定价模式中的模型分析.假设其他参数保持不变，令λ1=0.02，λ2=0.02，0.03，0.04，0.05，0.06，0.07，本节分析消费者损失厌恶程度对制造商利润、零售商利润、线上线下价格差额的影响(图9～图11).

由图9～图11可知，在其他参数不变的情况下，在双渠道差别定价模式中，制造商利润和零售商利润均随着损失厌恶程度的增大而增大，而线上价格与线下价格的差额随着损失厌恶程度的增大而减小.因此，考虑损失厌恶因素能够增加整个双渠道系统的利润，并减少线上与线下最优价格的差额.

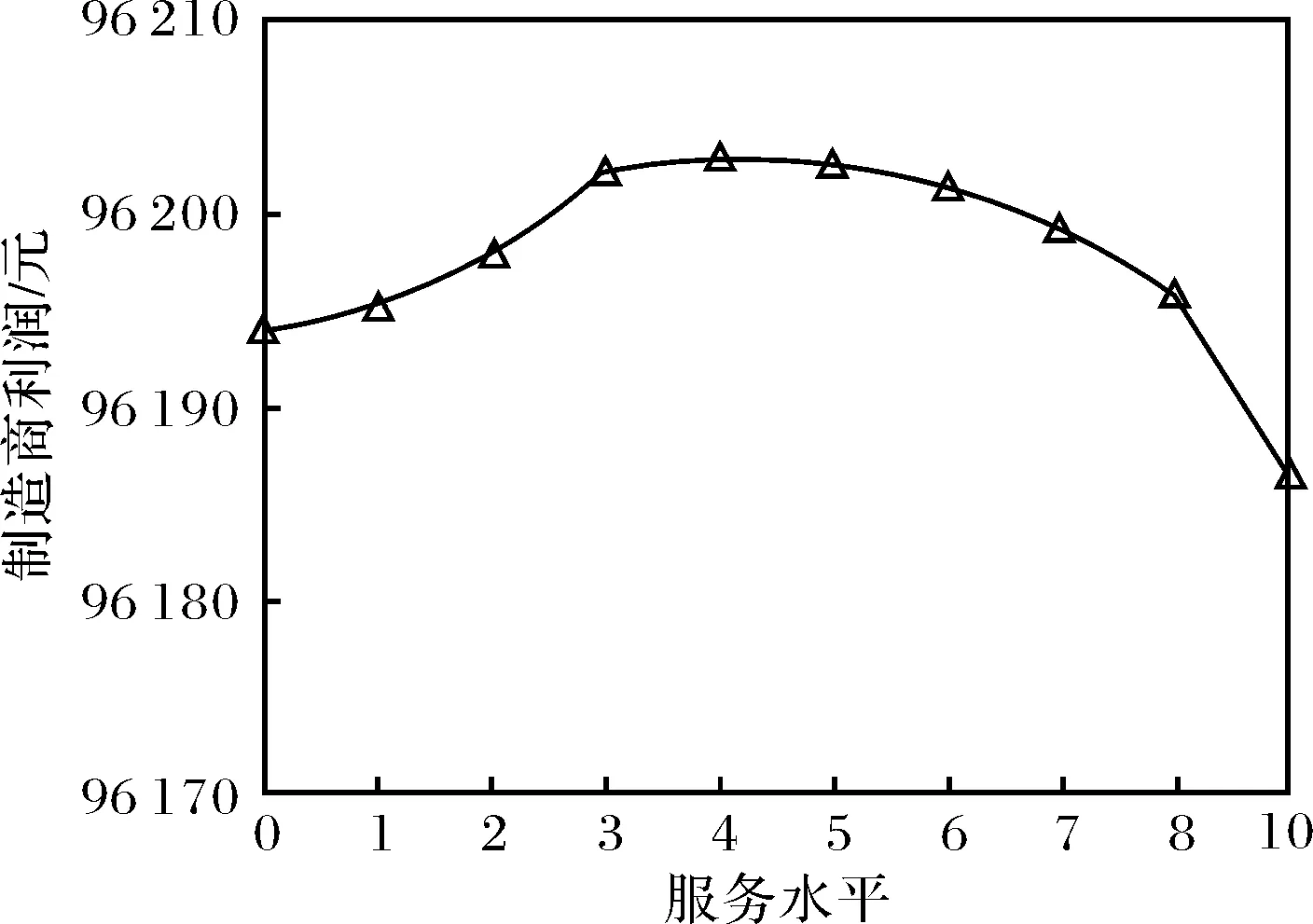
图6 双渠道统一定价模式下 零售商利润随服务水平的变化Fig.6 Variation of retailer profits with service level in a centralized distribution channel

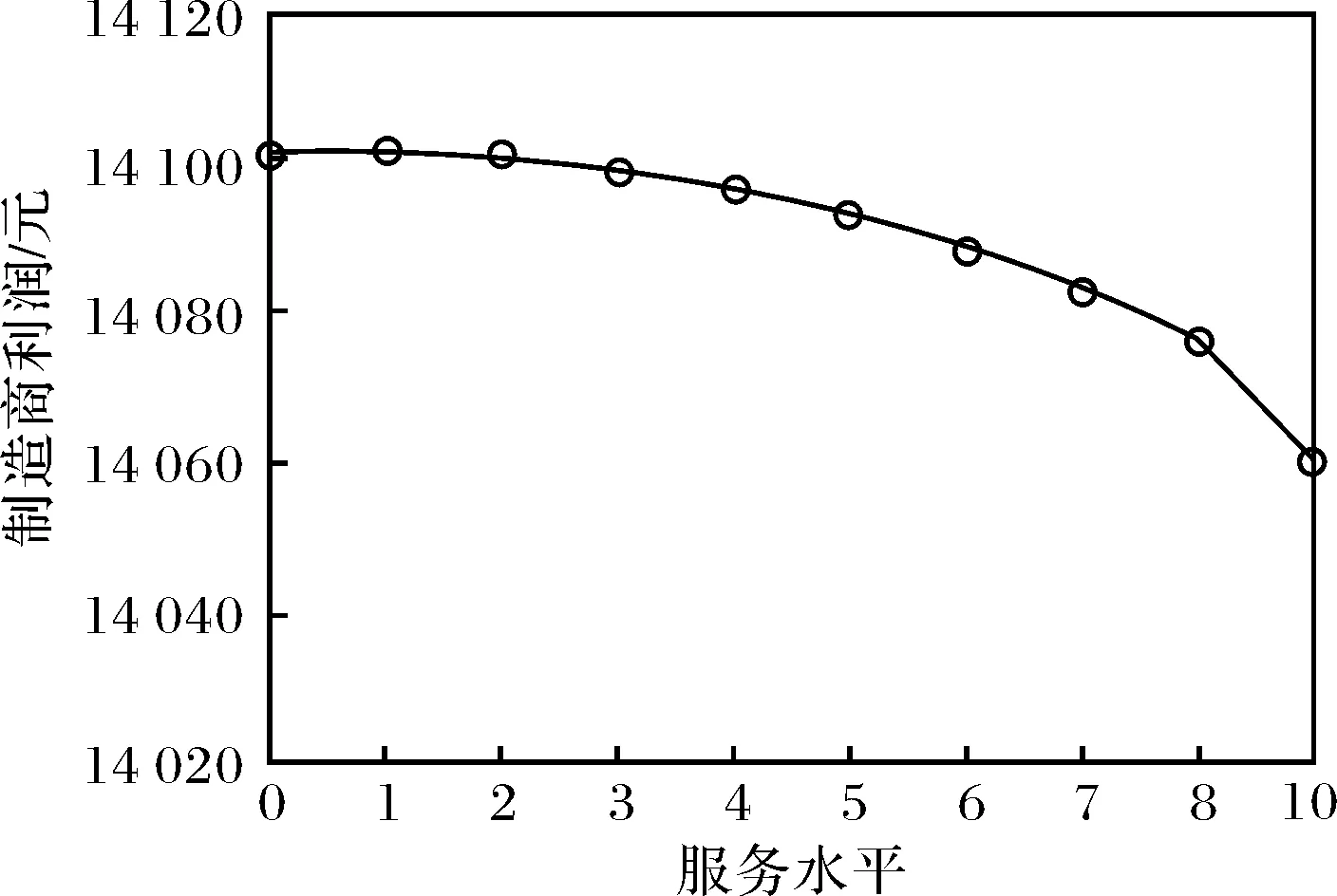
图7 单渠道定价模式下 零售商利润随服务水平变化Fig.7 Variation of retailer profits with service level in a single distribution channel

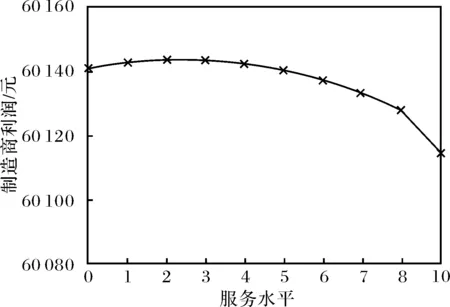
图8 双渠道差别定价模式下 零售商利润随服务水平的变化Fig.8 Variation of retailer profits with service level in a decentralized distribution channel

图9 损失厌恶程度对制造商利润的影响Fig.9 The change of manufacturer’s profits with loss aversion

图10 损失厌恶程度对零售商利润的影响Fig.10 The change of retailer’s profits with loss aversion

图11 损失厌恶程度对线上与线下价格差的影响Fig.11 The change of the difference between online and offline price with loss aversion

4结论

本文主要研究了双渠道定价问题，考虑了消费者损失厌恶因素，线上渠道允许退货以及线下渠道提供增值服务，得到如下结论.

1) 制造商利润随着零售商市场份额的增加而减少，零售商利润随着零售商市场份额的增加而增加.当零售商市场份额较小时，制造商应采取双渠道统一定价模式；当零售商市场份额较大时，应采取单渠道定价策略，即不开通线上渠道.对于制造商来说，在其它参数不变的情况下，选择何种策略要根据线上渠道或线下渠道的市场份额而定.

2) 随着退货率的增加，双渠道统一定价模式和双渠道差别定价模式下的制造商利润减少，零售商利润几乎不变，线上渠道的最优价格增大，线上需求减少.

3) 在其他参数不变的情况下，双渠道差别定价模式下的制造商利润、零售商利润均随着厌恶损失程度的增大而增大，而线上与线下的最优价格差额随着厌恶损失程度的增大而减小.因此，考虑消费者的损失厌恶行为对制造商和零售商的决策和利润有着重要的影响.

本研究假设市场中只存在单一产品，而现实中的消费市场往往存在着多种替代性产品，考虑多种产品替代效应的双渠道定价问题是进一步研究的方向.

[1] YAN D Q， LIU J J. Competitive pricing of mixed retail and e-tail distribution channels[J]. Omega， 2005， 33(3):235-247.

[2] TSAY A A， AGRAWAL N. Channel dynamics under price and service competition[J]. Manufacturing & Service Operations Management， 2000， 2(4):372-391．

[3] 罗美玲， 李 刚， 孙林岩. 基于增值服务的双渠道供应链竞争[J]. 工业工程与管理， 2011， 16(3):37-44．

[4] 刘咏梅， 廖 攀， 胡军华， 等. 考虑服务和退货的双渠道供应链定价问题研究[J]. 运筹与管理， 2015(3):79-87．

[5] 吴晓志， 陈 宏， 张 俊. 考虑服务竞争O2O供应链决策与协调[J]. 控制与决策， 2015， 30(8):1453-1461．

[6] SHULMAN J D， COUGHLAN A T， SAVASKAN R C. Managing consumer returns in a competitive environment[J].Management Science， 2011， 57(2): 347-362．

[7] FLAPPER S D P， GAYON J P，VERCRAENE S. Control of a production-inventory system with returns under imperfect advance return information[J]. European Journal of Operationan Research， 2012， 218:392-400．

[8] ANDERSON E T， HANSEN K， SIMISTER D， et al. How are demand and returns related？ theory and empirical evidence[R]. Evanston:Kellogg School of Management， Northwestern University， 2006．

[9] MOSTARD J，TEUNTER R.The newsboy problem with resalable returns: a single period model and case study[J]. European Journal of Operational Research， 2006， 169:81-96．

[10] 姚 忠. 风险约束下退货合同对供应链的协调性分析[J].管理科学学报， 2008， 11(3):96-105．

[11] YAO Z， LEUNG S C H， LAI K K. Analysis of the impact of price-sensitivity factors on the returns policy in coordinating supply chain[J]. European Journal of Operational Research， 2008， 187(1):275-282．

[12] 陈菊红， 付 侠， 苏菊宁. 三级短生命周期产品供应链退货协调研究[J]. 工业工程与管理， 2011， 16(1):28-31．

[13] NASIRY J， POPESCU I. Dynamic pricing with loss-averse consumers and peak-end anchoring.[J]. Operations Research， 2011， 59(6):1361-1368．

[14] 柳 键， 邱国斌， 黄 健. 考虑缺货损失情形下损失厌恶零售商的订货决策[J]. 控制与决策， 2012， 27(8)： 1195-1200．

[15] 王 虹， 周 晶. 零售商参与的供应链协调机制研究[J]. 统计与决策， 2009(3):180-182．

[16] GAN X，SETHI S，YAN H.Channel coordination with a risk neutral supplier and a downside risk-averse retailer[J]. Production and Operations Management， 2005， 14:80-89．

[17] 张霖霖， 姚 忠. 考虑顾客退货时在线企业的定价与订货策略[J]. 管理科学学报， 2013， 16(6):10-21.

[18] 薛顺利，徐 渝，宋悦林，等.电子商务环境下定价与退货策略整合优化研究[J]. 运筹与管理， 2006， 15(5):133-137．

[19] 徐 峰， 侯云章， 高 俊. 电子商务背景下制造商渠道定价与再制造策略研究[J]. 管理科学， 2014， 27(2):74-81．

附录

性质1

可得基本定价策略下的最优销售价格和批发价格.

性质2

性质3

性质4

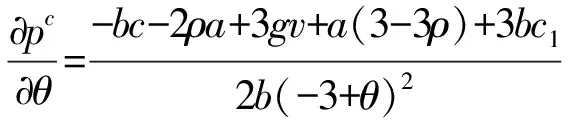
又c≤w≤pc，

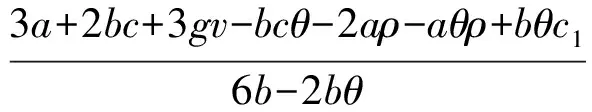
化简得到2aρ≤3a+bθc1+bcθ-aθρ-4bc，

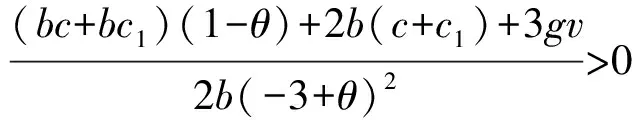
性质5

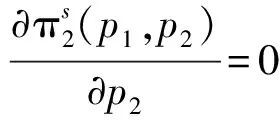
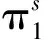
从而可得线上渠道和线下渠道的最优价格.

性质6

证明

0，

性质7

λ1(4b+3λ2))(-λ1(4b(-1+θ)(bw+a(-1+ρ))+

((-1+θ)(-2bc+5bw+3a(-1+ρ))+

(b+λ2)(4b(-1+θ)(+bw+a(-1+ρ))+

2(-(-1+θ)(bc-2bw+ρa)+bθc1)λ2+

(2b(b+λ2)+λ1(2b+λ2))2).

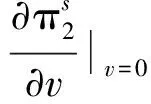
反之，易可证.

Pricing policies for a dual-channel supplychain considering loss aversion and returns

DUAN Yongrui， DAI Xiangyan

(School of Economics and Management， Tongji University， Shanghai 200092)

In this paper， the pricing policies for dual-chain supply is studied， which consists of a manufacturer and a retailer in a bilateral monopoly setting. Pricing model of online and offline is established in which consumers’ loss aversion is considered with added value by offline channel and returns from online channel. The centralized and decentralized pricing policies based on Stacklberg games are formulated， and the optimal prices along with expected profits are obtained. The numerical analysis showed that the centralized pricing policy is better when retailer’s market share is very large， otherwise， it’s better not to open the online channel for the manufacturer; the profits of manufacturer and retailer decrease with the increase of return rate both in centralized and decentralized pricing channel; the profits of manufacturer and retailer increase with the extent of loss aversion and the optimal price difference between online and offline decreases with the extent of loss aversion in decentralized channel．

loss aversion; dual-channel supply chain; returns

2016-07-05.

国家自然科学基金项目(71371139，71532015); 上海市曙光计划项目(13SG24)．

段永瑞(1975-)，博士，教授，博士生导师，主要研究领域为服务运作管理.E-mail: yrduan@163.com.

1000-1190(2017)01-0084-09

F274

A