双挡浪墙结构海堤的多道齿墙内力计算分析
沈靠山(浙江省钱塘江管理局勘测设计院,浙江 杭州 310016)
双挡浪墙结构海堤的多道齿墙内力计算分析
沈靠山
(浙江省钱塘江管理局勘测设计院,浙江 杭州 310016)
在秦山核电厂海堤加高工程中,堤顶挡浪墙设置内外两挡浪墙,并设置三道齿墙抵抗水平波浪力,设计过程中采用常规理论及有限元法计算多道齿墙受力,根据计算成果分析研究认为,对复杂结构进行合理简化、假定,采用常规理论计算可满足工程设计需要,水平荷载主要由齿墙侧被动土压力承担,多道齿墙受力主要与被动土压力侧土体刚度有关,填土刚度大,被动土压力发挥程度高,承担的水平土压力相对较大.
抗滑稳定;挡浪墙;齿墙;被动土压力
1 项目概况
挡墙抗滑稳定不满足要求时,通常方法是通过增加齿墙,增大抗滑能力[1].本文主要研究在较大水平荷载作用下,多道齿墙结构内力分布情况.通过计算分析秦山一期海堤双挡浪墙结构的抗滑稳定,计算工况为抵御设计基准洪水(10.01 m)[2-3],并叠加相应风浪的侵袭.该双挡浪墙结构由国内专家多次论证,及波浪模型试验确定,海堤堤顶结构(见图1).
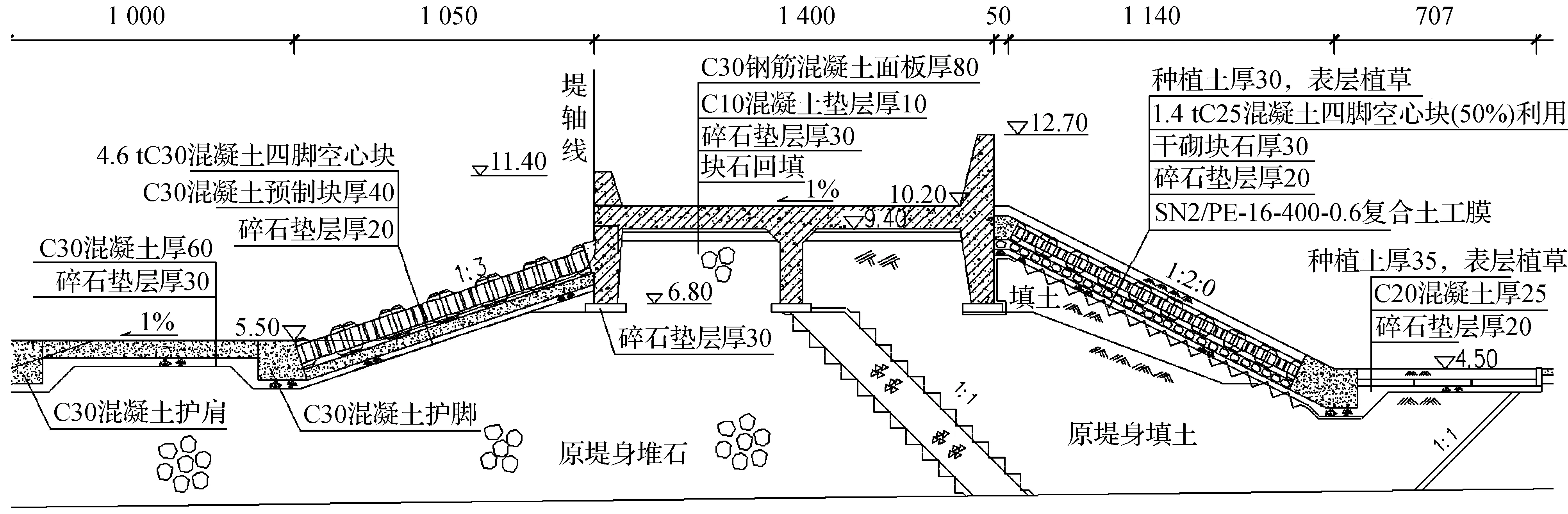
图1 海堤设计典型断面图
由于受到波浪力较大(波浪作用在前挡浪墙时,波浪力为554 kN/m;波浪作用在后挡浪墙时,波浪力为315 kN/m,由波浪模型试验确定),靠挡墙自身重量难以满足抗滑要求.为满足抗滑要求,挡浪墙结构采用3道齿墙抗滑.
由于堤顶结构复杂,地基为块石混合料和粘土两种材料.为保证结构设计合理,必须计算各个部件的内力,以满足结构配筋需要.设计过程中采用多种方法计算分析齿墙受力情况.
2 挡墙受力条件
2.1 研究方法
计算工况:根据波浪力作用在前后挡浪墙上,分为两种工况:工况1为波浪力作用在前挡浪墙;工况2为波浪力主要作用在后挡浪墙.
复杂结构内力计算方法包括常规简化计算、结构力学、有限元计算等多种方法.本文采用两种计算方法:(1)常规简化计算法:即对结构进行合理的简化、假定,根据土力学、材料力学、结构力学等基本原理,将齿墙作为单独分离体,将混凝土结构作为一个刚体,不考虑上部结构基础对齿墙的弯矩影响.(2)平面有限元法:计算采用的程序是河海大学岩土工程研究所研制的BCF平面有限元比奥固结程序,混凝土作为线弹性材料,对堆石料、地基、原堤身填土等土料,采用线弹性模型.[4-5]
为便于对结果进行整理分析,对堤顶挡浪墙结构进行编号(见图2).
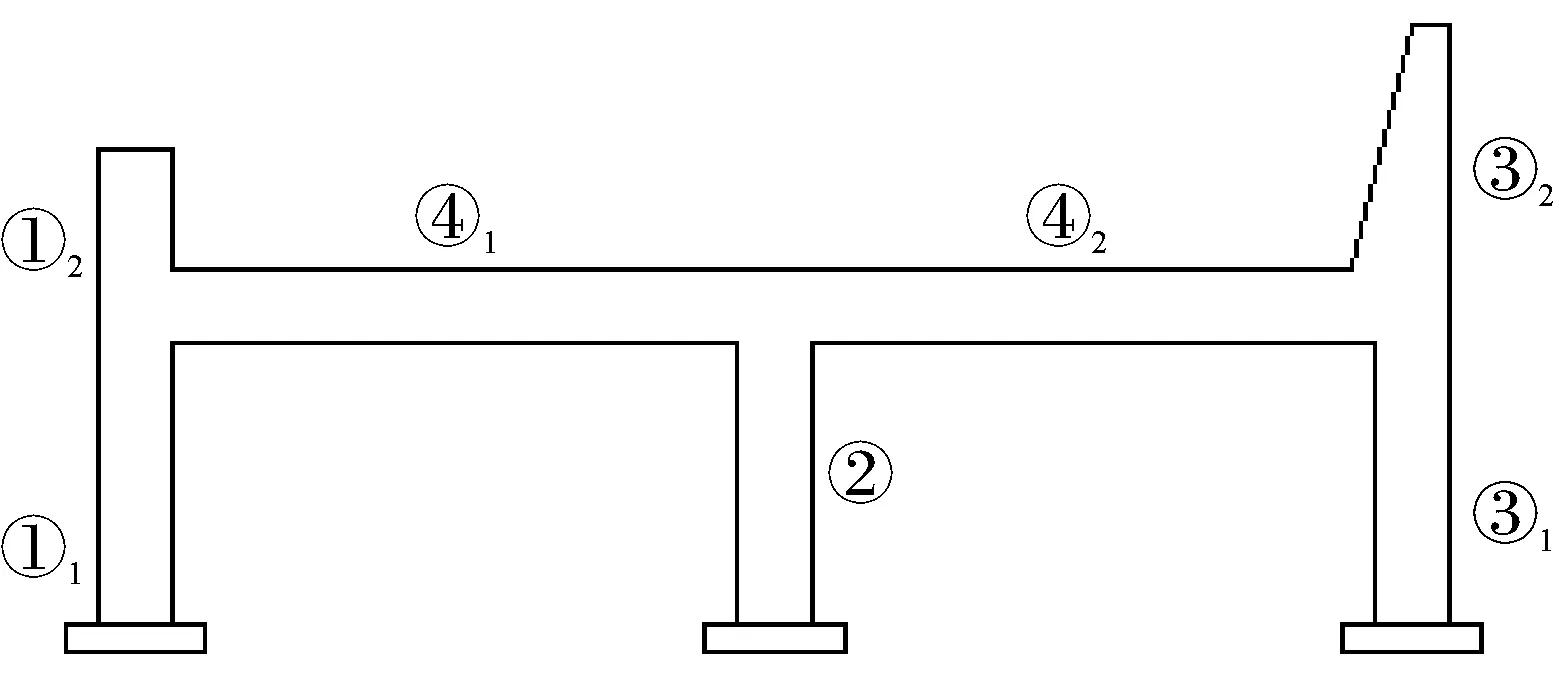
图2 海堤堤顶防浪墙结构各构件编号示意图
2.2 计算主要参数
挡浪墙结构受到的外力主要有自重、基底摩擦力、水压力、波浪压力、波浪浮托力等,其中波浪压力、波浪浮托力由水槽模型试验测定,其余荷载按相关规范计算而得.主要计算参数:前齿墙与中间齿墙之间填土为块石混合料,浮重度取11 kN/m3,湿重度采用20 kN/m3,内摩擦角取38°,堤身堆石压缩模量60 MPa、泊松比0.2,中间齿墙与后齿墙之间填土为粘性土,天然重度采用18.5 kN/m3,内摩擦角取20°,粘结力取15 kPa,底板摩擦系数取0.6,堤身填土压缩模量取10.8 MPa,泊松比取0.25.
块石混合料静止侧压力系数取0.4;粘性土的静止侧压力系数较复杂,与土的种类、密度、含水量、固结度等因素有关[6],考虑计算工况出现机率较小,且出现时间较短,堤身填土为坚硬状态,泊松比为0.25;参考类似工程经验,取填土的静止侧压力系数为0.33.
3 常规理论计算成果及分析
齿墙上游土压力按照主动土压力考虑[7],齿墙下游土体处于塑性平衡状态,土压力介于静止与被动土压力之间,假定被动土压力的发挥程度为R,DG面后侧为坡面临空的填土,假定该面上的被动土压力发挥程度为0.8R.前后挡浪墙受波浪力作用下挡墙结构的受力示意图(见图3,图4).
考虑到齿墙内侧被动土楔的存在,齿墙内侧只有被动土压力,不考虑底板与基础之间的抗滑摩阻力,假定作用在结构上的波浪力及齿墙前主动土压力均由齿墙内侧被动土压力承担.当齿墙后被动土压力全部发挥时,1#齿墙最大弯矩约为464 kN·m,2#齿墙最大弯矩约为392 kN·m,3#齿墙最大弯矩约为210 kN·m.
考虑到混凝土结构刚度较大,认为挡浪墙结构自身变形可忽略不计,齿墙之间块石混合料、黏性土体积变形相同.在相同变形条件下,不同土体产生的被动土压力与其变形模量成正比关系.[8]
根据以上分析,当波浪力作用在前挡浪墙上时,波浪力为554 kN,计算1#齿墙被动土压力为480.2 kN,被动土压力发挥程度为0.81,2#、3#齿墙被动土压力103 kN,被动土压力发挥程度分别为0.24、0.39,三道齿墙最大弯矩分别为130 kN·m、74 kN·m、35 kN·m.当波浪力作用在后挡浪墙上时,波浪力为315 kN,计算1#齿墙被动土压力为480.2 kN,被动土压力发挥程度为0.81,2#、3#齿墙被动土压力103 kN,被动土压力发挥程度分别为0.24、0.39,三道齿墙最大弯矩分别为150 kN·m、23 kN·m、-22 kN·m.
由以上计算可知,水平荷载主要1#齿墙承担,1#齿墙内侧为块石混合料,弹性模量小,被动土压力发挥程度高,2#、3#齿墙承担水平波浪力较小,1#齿墙在被动土压力作用下弯矩最大,由于3#齿墙外侧土体为临空面,被动土压力发挥较小,内侧土体存在竖向荷载,齿墙内侧主动土压力稍大,会出现弯矩为负值,即齿墙内侧受拉.
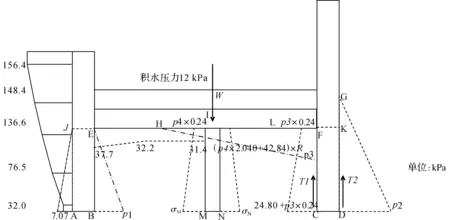
图3 波浪压力作用防浪墙结构前墙时受力分布图
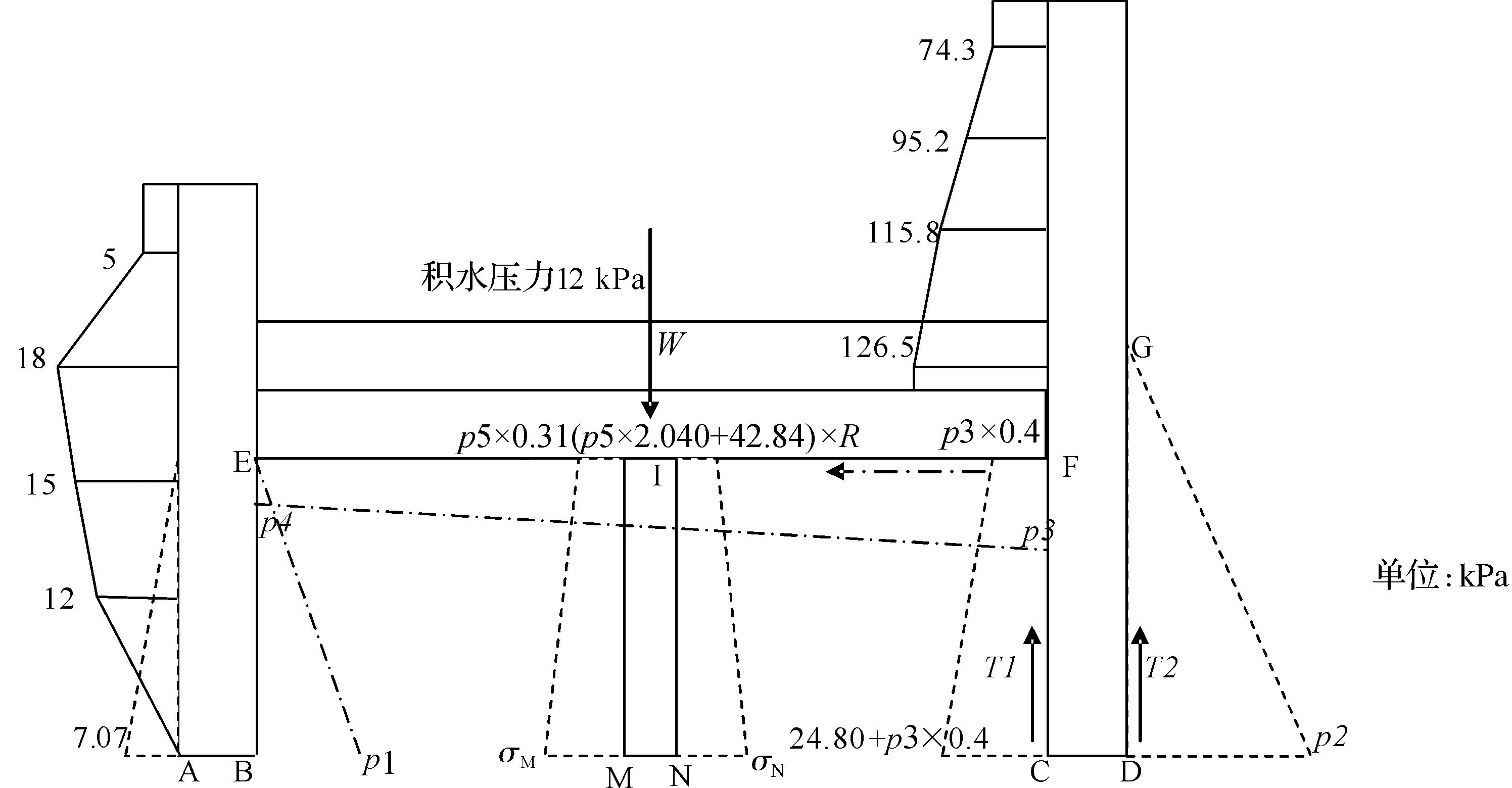
图4 波浪压力作用防浪墙后墙结构后墙时受力分布图
4 有限元法计算成果及分析
4.1 工况1的计算成果及分析
波浪力作用在前挡浪墙时,三道齿墙弯矩(见图5~图7),底板弯矩(见图8).1#齿墙上部为前挡浪墙,在波浪力的作用,最大弯矩为190.43 kN·m;1#齿墙受被动土压力影响向堤外侧弯曲,最大弯矩为155.03 kN·m,位于齿墙与底板的交界处;2#齿墙最大弯矩为53 kN·m;受上游浪压力作用;3#齿墙外侧出现较大被动土压力,最大弯矩位于齿墙与底板的交界处,为131.83 kN·m.
底板受中间齿墙的影响,弯矩图分成两段:左半段受地基土反力及扬压力的作用,表现为向上弯曲,最大弯矩在左端支座处,为-289.92 kN·m,跨中弯矩为68.51 kN·m,右端支座处弯矩为160.45 kN·m;右半段弯矩不大,最右端弯矩113.83 kN·m.
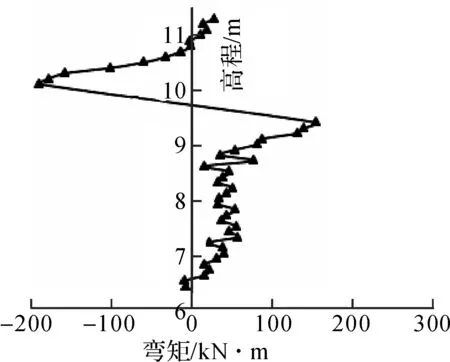
图5 1#齿墙及挡浪墙工况1弯矩图

图6 2#齿墙及挡浪墙工况1弯矩图
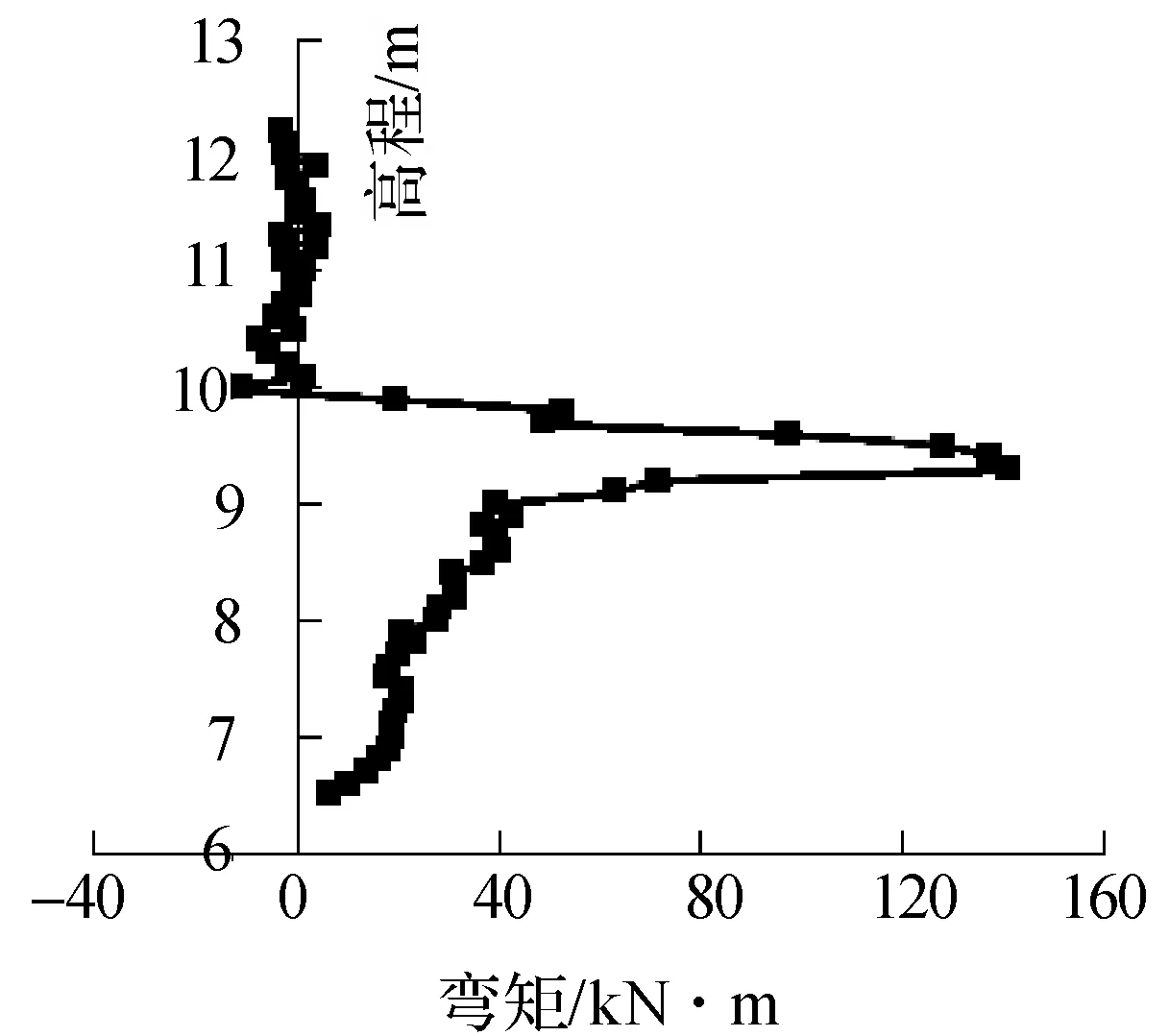
图7 3#齿墙及挡浪墙工况1弯矩图
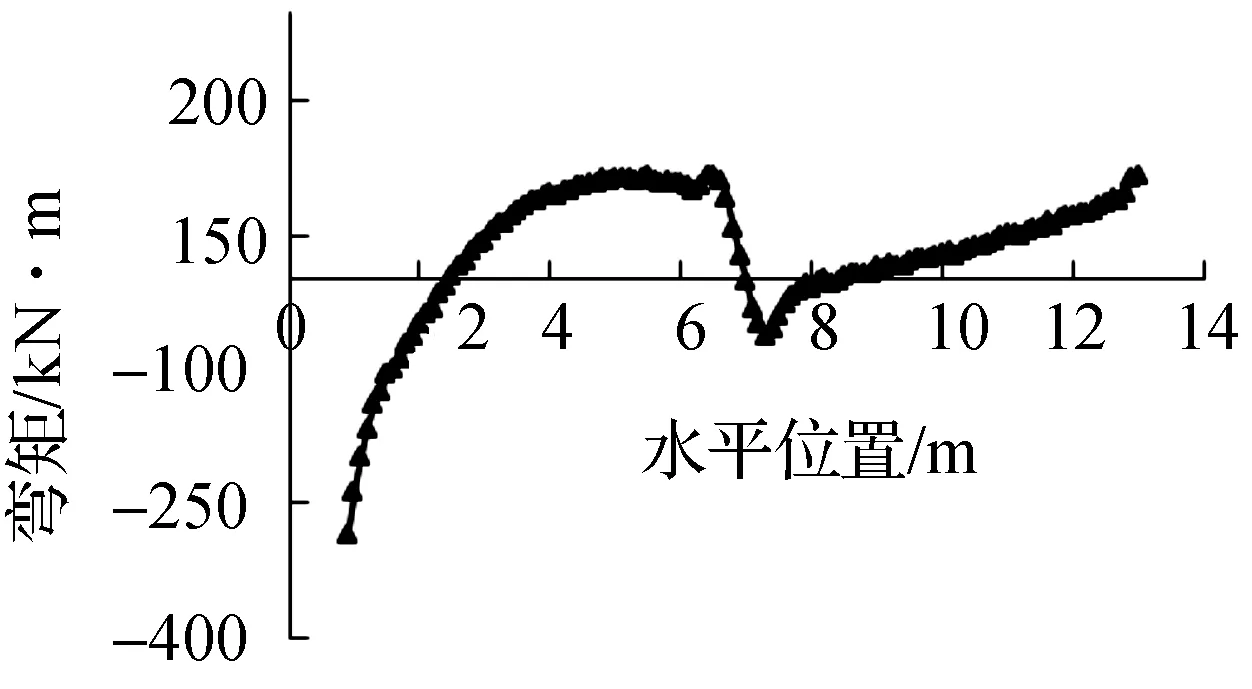
图8 4#底板工况1弯矩图
4.2 工况2的计算成果及分析
波浪力作用在后挡浪墙,堤顶结构弯矩(见图9~图12).1#齿墙受被动土压力作用,最大弯矩为149.53 kN·m,位于齿墙与底板的交界处;2#齿墙最大弯矩为54 kN·m;3#齿墙上部为后挡浪墙结构,受波浪压力作用,后挡浪墙向堤内侧弯曲,弯矩最大为-391.84 kN·m;3#齿墙弯矩较复杂,9.0 m高程以下弯矩为负值,且弯矩与高程呈线性关系,9.0 m高程以上弯矩为正值,在齿墙与底板交界处弯矩突变.
3#齿墙下部主要受土压力作用,由于齿墙内侧存在竖向荷载,外侧为临空坡面,被动土压力不能完全发挥,出现主动土压力大于外侧被动土压力,齿墙弯矩出现负值;齿墙与底板交界处弯矩出现突变,主要受底板及上部结构弯矩影响.
挡浪墙结构底板受中间齿墙的影响,弯矩图分成两段,均呈线性分布.右半段右端支座处弯矩最大,为357.36 kN·m,跨中弯矩为81.79 kN·m,左端支座处弯矩为-83.31 kN·m;左半段最左端弯矩-148.77 kN·m,最右端弯矩118.72 kN·m.
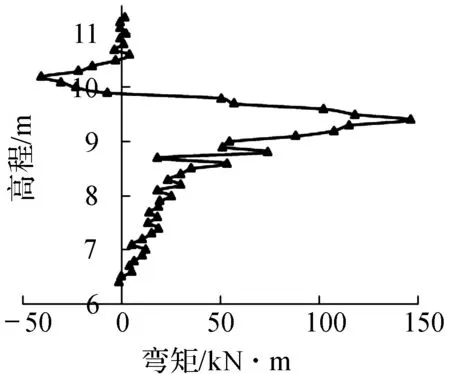
图9 1#齿墙及挡浪墙工况2弯矩图
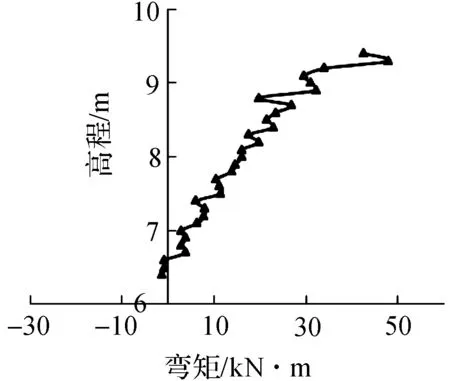
图10 2#齿墙工况2弯矩图
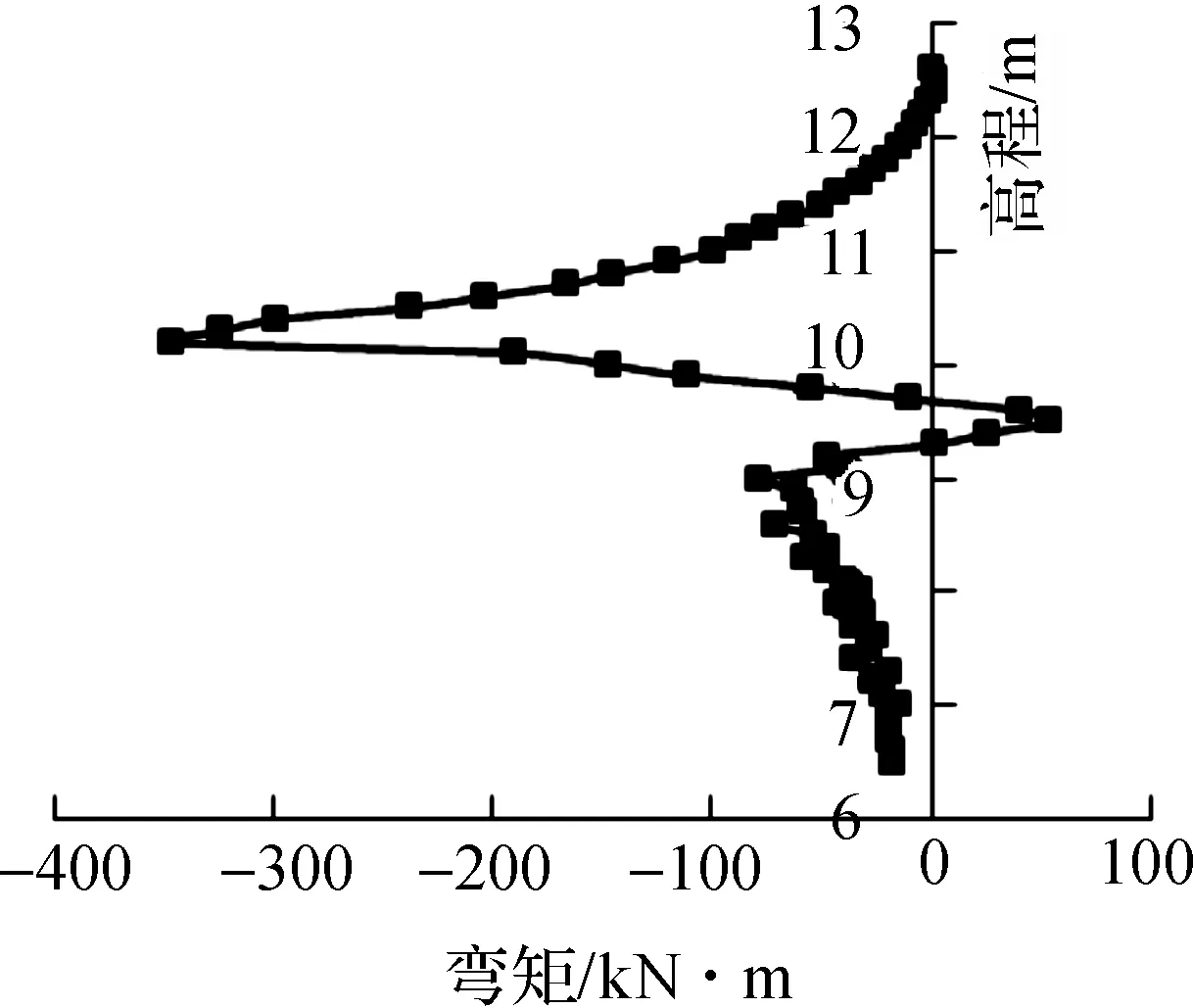
图11 3#齿墙及挡浪墙工况2弯矩图
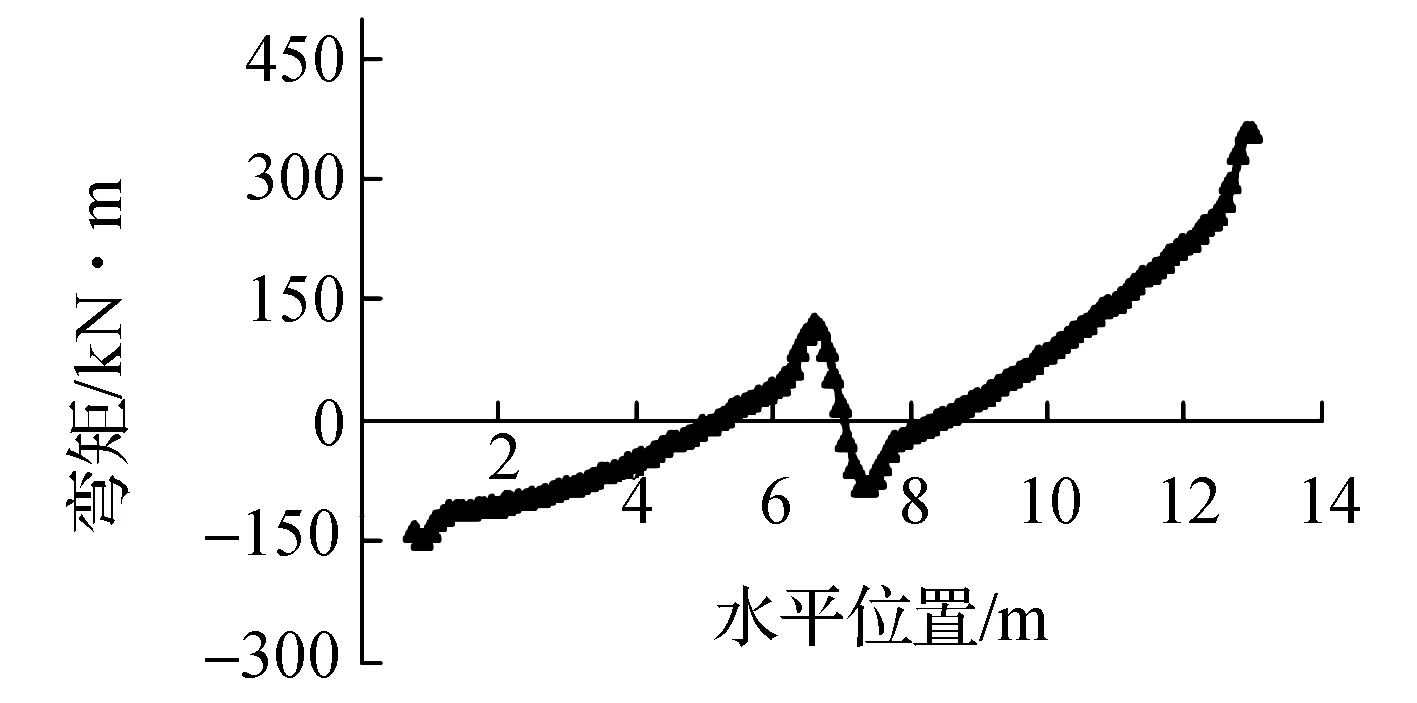
图12 4#底板工况2弯矩图
两种方法计算齿墙的最大弯矩(见表1),由计算成果可以得出:(1)1#、2#齿墙弯矩计算成果接近,3#齿墙弯矩相差较大;图7显示,弯矩在齿墙与底板交接除出现突变,突变前弯矩约为40~50 kN·m,与理论简化计算接近,因此可认为3#齿墙上段弯矩约40~50 kN·m;(2)不考虑上部结构对齿墙弯矩的影响,水平荷载主要由1#齿墙承担.
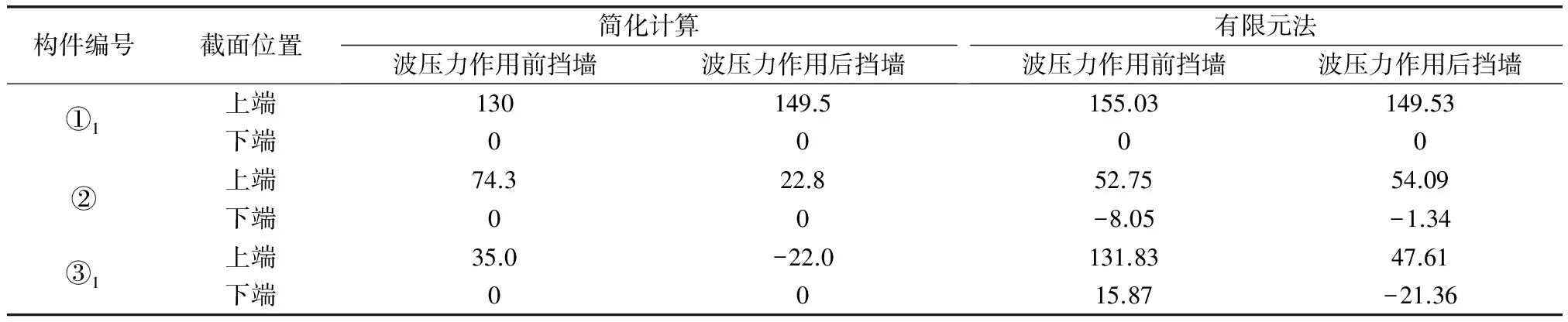
表1 不同计算方法计算齿墙最大弯矩成果表 单位:kN·m
由有限元计算3#齿墙工况二弯矩图显示:弯矩在齿墙与底板交接除出现突变,突变前弯矩约为-80 kN·m,与理论简化计算受弯方向一致.由后挡浪墙底部弯矩为-391.84 kN·m,底板右段右端弯矩为357.36 kN·m,可知3#齿墙与底板交接处弯矩47.61 kN·m由上部结构引起,说明3#齿墙下端弯矩主要由内外土压力引起,端部主要受上部结构影响.
根据简化计算法及有限元计算成果,在水平荷载作用下,各道齿墙承担的水平力与齿墙内侧土体刚度有关.在波浪力作用下挡浪墙结构产生一定量的变形,齿墙内侧土体弹性模量大时,被动土压力发挥程度较大,弹性模量小的土体被动土压力发挥程度较小.
5 结 论
(1)对复杂结构进行合理简化、假定,采用土力学、材料力学等基本理论计算,计算成果接近结构实际受力,可满足工程设计需要.
(2)挡浪墙多道齿墙受力与被动土压力侧土体刚度有关,填土刚度大,被动土压力发挥程度高.根据计算分析可知,水平浪压力主要由1#齿墙承担,承担的水平力65%以上.
(3)长齿墙下部主要受内外侧土压力作用,受水平波浪力作用位置的不同,1#、2#齿墙受力特征基本相同,主动土压力均小于被动土压力,齿墙上端弯矩内侧受拉;3#齿墙受力特征受波浪力作用位置的影响,当波浪力主要作用在后挡浪墙时,会出现主动土压力大于被动土压力,齿墙下部会出现弯矩为负值,即齿墙内侧受拉,3#齿墙与底板交接处弯矩受上部作用力影响较大.
[1] 钱家欢.土工原理与计算[M].北京:中国水利水电出版社,1995.
[2] 黄世昌.秦山核电厂扩建项目(方家山厂址)设计基准洪水位问题补充研究[R].杭州:浙江省水利河口研究院,2007.
[3] 浙江省河口海岸重点实验室.秦山核电厂扩建工程(方家山核电工程)设计基准洪(低)水位专题报告[R].杭州:浙江省水利河口研究院,2008.
[4] 闫勋念.粗粒土力学特性三轴试验与模拟研究[D].南京:河海大学,2016.
[5] 张 兵,高玉峰.堆石料应力—应变关系的拟合方法研究[J].岩土力学,2010,31(7):2342-2346.
[6] 姜 朴.粘性土的静止侧压力系数[J].河海大学学报(自然科学版),1963(S1):61-65.
[7] 章瑞文.挡土墙主动土压力理论研究[D].杭州:浙江大学,2007.
[8] 王俊杰,朱俊高,魏 松.刚性挡土墙被动土压力的计算及影响分析[J].哈尔滨工业大学学报,2004,36(11):1483-1486.
Calculation and Analysis on Internal Force of Multichannel Key-wall
SHEN Kao-shan
(Reconnaissance and Design Institute of Qiantang River Administration, Hangzhou 310016, China)
In the heightening project of Qinshan Nuclear Power Plant, an inter-outer wave wall is constructed on the top of the seawall, as well as three courses of key-wall to resist the horizontal wave force. In the design process, conventional theory and finite element method is adopted to calculate multichannel tooth wall stress. The calculation results prove it reasonable to simplify and assume a complex structure, and conventional theoretical calculation can meet the requirements of engineering design. The horizontal load is mainly composed of wall lateral passive earth pressure, while the multichannel tooth wall stress is mainly from passive earth pressure and lateral stiffness of soil. The stiffer the filled soil is, the higher degree the passive earth pressure plays, therefore, the relatively larger the soil pressure will be.
anti-sliding stability; wave wall; key-wall; passive earth pressure
2016-10-26
沈靠山(1984-),男,江苏连云港人,硕士,工程师,主要从事水工建筑物设计及研究工作.
TV641
A
1008-536X(2017)02-0024-05

