传力洞截面对拱坝坝肩稳定的影响

吴党中，王茂荣(.浙江中水工程技术有限公司，浙江 杭州 3000；.浙江建设职业技术学院，浙江 杭州 33)

传力洞截面对拱坝坝肩稳定的影响

吴党中1，王茂荣2
(1.浙江中水工程技术有限公司，浙江 杭州 310020；2.浙江建设职业技术学院，浙江 杭州 311231)

传力洞对处理拱坝软弱破碎带基础具有较好的效果，实际工程中应用很普遍.通过建立拱坝及其基础的三维有限元模型，分析了不同半径传力洞对软弱基础中特定滑裂面抗滑稳定安全系数的影响，结果表明：传力洞的设置对软弱破碎带内的特定滑裂面抗滑安全通常是有利的，但当传力洞半径设置不当时，有可能反而不利滑裂面的抗滑稳定.

坝基处理；传力洞；断层破碎带；有限元

对于合适的坝址条件，拱坝是一种既经济又安全的坝型.相对于同一坝址处相同高度的其它坝型，拱坝一般工程量较省，而超载能力更强.虽然拱坝对建坝基础的要求较高，但综合基础处理后的工程造价，往往仍然低于其它坝型.目前，全世界200 m以上的大坝，有一半以上采用拱坝坝型[1].我国已经建成的超高拱坝有拉西瓦(250 m)，锦屏一级(305 m)，构皮滩(225 m)，小湾(292 m)和溪洛渡(285.5 m)等.

根据拱坝的受力特点，拱坝的坝肩稳定是拱坝设计成败的关键，而坝肩岩体的完整性和坚固程度是影响坝肩稳定的重要因素.完全符合设计要求的拱坝天然坝基在实际工程中很少出现，一般工程中均需对基础进行相应的处理，以满足大坝受力要求.对于拱坝坝肩基础而言，有时会出现一定范围的软弱夹层或破碎带，当通过表层处理(如灌浆、深挖回填)工程措施不能满足要求或者代价太大时，采用设置传力洞(有时也称抗剪洞)穿过软弱破碎带的处理方式能够很好地解决这一问题[2-3].实践证明，传力洞对增强拱坝坝肩稳定是行之有效的拱坝基础深部处理措施，正被应用于越来越多的工程之中[4-10].

传力洞最佳直径理论值[11]，在相关文献中已有论述.然而在实际工程设计过程中，很多工程师通常以求稳的心理，趋向设计尽可能大截面的传力洞，认为这样能获得更大的坝肩稳定安全系数.在有些情况下，规模更大的传力洞确实能够带来更大的坝肩稳定安全系数，但也有一些工程，尤其是一些坝高较低的拱坝，截面大的传力洞，对坝肩稳定的增稳效果，反而不如截面小的传力洞.本文将通过建立三维有限元模型，分析不同截面传力洞对拱坝坝肩稳定的影响，以期对实际工程起参考作用.

1 计算模型与方法

1.1 计算模型

以下通过对一座38 m高的拱坝，以不同截面传力洞处理基础软弱破碎带后，对坝肩稳定安全系数的变化情况分析，来讨论传力洞不同截面对特定坝肩滑裂面的抗滑稳定影响.

坝址河谷深切呈略开张“V”形，河床宽度30 m，左右岸坡坡度1 ∶1.河段为正交谷，岸坡形态为平直型.拱坝建基面岩体大部分完整坚硬，在左岸离坝底15～25 m高程处存在一软弱破碎带夹层，软弱夹层的深度为20 m.假设软弱夹层内部存在一条可能影响坝肩稳定的结构面，结构面倾角为竖直向下，走向与坝轴线成30°夹角.对该不良地质情况采取的处理措施是设置C15混凝土传力洞加固.传力洞的截面为圆形，其半径分别采用1.0 m(最小施工洞径)、1.5 m、2.0 m、2.5 m和3.0 m(接近该层拱坝的拱端厚度)，传力洞水平布置，每种半径的传力洞布置方向均与特定滑裂面走向成80°的交角.

建基面岩体物理力学参数为：

(1)完整基岩之间抗剪摩擦系数f=1.0，滑裂面之间抗剪摩擦系数f=0.6.完整岩体的变形模量为10 GPa，泊松比为0.25；软弱夹层的岩体的变形模量为1.0 GPa，泊松比为0.33.

(2)混凝土拱坝为混合线型双曲变厚拱坝，最大坝高38 m，坝体材料为C15混凝土.拱坝拱冠梁处坝顶厚度3.0 m，坝底厚度8.24 m，厚高比0.22，坝顶中心线弧长110 m，弧高比2.88.坝体最大中心角69.17°.

(3)坝体材料弹模1.8×104N/mm2，泊桑比0.167，容重24 kN/m3，线膨胀系数1×10-5/℃，导温系数3 m2/月.基岩变模为1.0×104N/mm2，泊桑比0.167.

(4)坝基的计算范围为：基础的深度为最大坝高的1倍，左右岸及拱坝上游基础各延伸1倍最大坝高，下游基础延伸2.5倍最大坝高.

(5)计算软件采用ANSYS有限元计算分析软件，有限元模型的整体坐标系定义如下：拱坝拱冠梁上游顶点为坐标原点，右岸为+X方向，+Y轴铅直向下，Z轴指向下游.

(6)坝体采用8节点SOLID45单元模拟，一般岩体采用8节点SOLID65单元模拟，软弱破碎带范围岩体及传力洞采用20节点SOLID186单元模拟.

拱坝整体有限元模型及坝体模型(见图1，图2).

图1 拱坝整体三维有限元模型

图2 坝体(含传力洞)三维有限元模型

1.2 计算方法

本文讨论某个特定的传力洞，其洞轴线方向一定，当传力洞的截面尺寸发生变化时，其对特定滑裂面的抗滑稳定安全系数的影响.为此需要假定各不同截面尺寸传力洞，并分别计算各种不同截面传力洞与无传力洞作用时滑裂面抗滑稳定安全系数，比较各不同截面传力洞处理前后滑裂面抗滑稳定安全系数的变化情况.

在计算时假设滑裂面走向与坝轴线的夹角为30°，考虑到实际工程可能情况，将传力洞的轴线方向与滑裂面走向布置成80°交角(见图3)，分别分析有无设置传力洞的情况下，拱坝坝肩稳定安全系数变化情况.

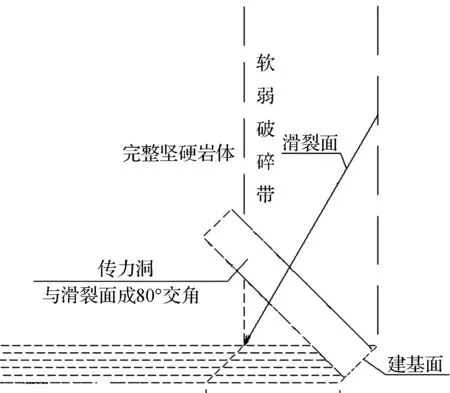
图3 传力洞与滑裂面平面位置示意图

根据《混凝土拱坝设计规范》(SL282—2003)，拱坝坝肩稳定(点、面)安全系数的抗剪公式为：

(1)

(2)

式中：Kp—特定软弱结构面上计算点的抗滑稳定安全系数，简称点安全系数；

Kf—沿特定软弱结构面的抗滑稳定安全系数，简称面安全系数；

fi—计算点处软弱结构面的抗剪摩擦系数；

σi—计算点处软弱结构面的法向压应力；

τi—计算点处软弱结构面的剪应力在滑动方向上的分量(即切向应力)；

Ai—计算点所代表的软弱结构面的面积.

计算时取滑裂面的单位宽度.沿滑裂面走向将其均分为20小段，取每小段的首尾两点作为应力计算点，共计21个应力计算点.每个应力计算点所代表的滑面范围为与该点相连的两小段滑面之和的一半.

通过有限元计算，可以得到各应力计算点的六个应力分量，即σix、σiy、σiz、τixy、τiyz和τixz.

设滑动面的外法线方向余弦分别为l，m，n.根据弹性力学的有关原理，各应力计算点所代表结构面的应力分量pix、piy和piz为：

(3)

则各应力计算点所代表结构面上的法向压应力σi为：

σi=l·pix+m·piy+n·piz

将上式展开可得:

σi=l2σix+m2σiy+n2σiz+
2lmτixy+2mnτiyz+2nlτizx

(4)

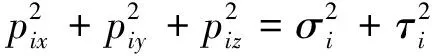
可得各应力计算点所代表结构面上的切应力τi为：

(5)

将各点的σi和τi代入公式(1)和式(2)中，就可以求得可能滑动结构面各计算点的点抗滑安全系数Kp和结构面的面抗滑安全系数Kf.

2 计算成果分析

针对设置传力洞处理和未设置传力洞处理两种情况，分别建立拱坝和地基的整体分析三维有限元模型，对未布置传力洞和布置了不同截面传力洞的同一滑裂面的点、面抗滑稳定安全系数进行分析计算.设置传力洞后滑裂面各点抗滑安全系数与未设置传力洞的滑面点抗滑安全系数比较(见图4～图8)，表中横坐标表示滑面上各计算点，纵坐标表示各点的抗滑安全系数.

不同半径传力洞情况下滑面的面抗滑稳定安全系数(见表1).

图4 传力洞半径R=1.0 m

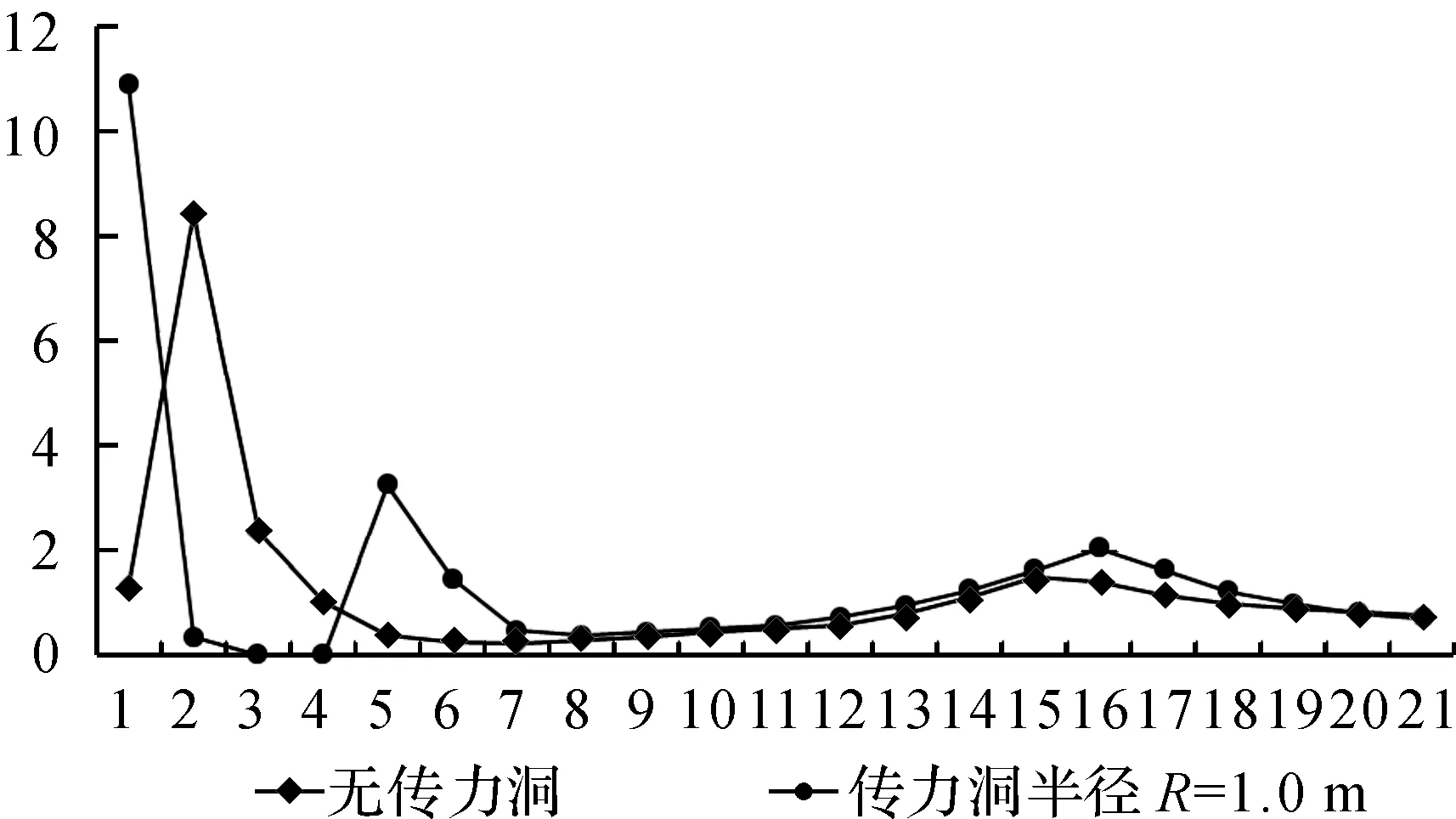
图5 传力洞半径R=1.5 m

图6 传力洞半径R=2.0 m

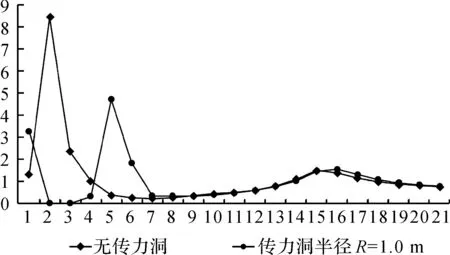
图7 传力洞半径R=2.5 m

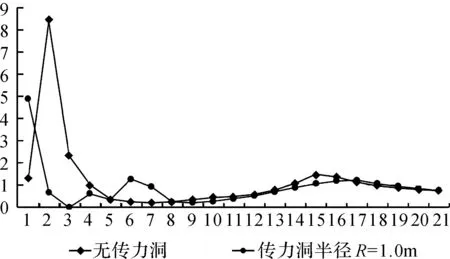
图8 传力洞半径R=3.0 m

表1 不同半径传力洞情况下滑裂面的面抗滑稳定安全系数表

传力洞半径/m无传力洞1．01．52．02．53．0面安全系数0．7150．8550．9320．9140．8090．752安全系数增幅/%/19．5829．0927．8313．155．17

根据有限元计算结果可见，设置了传力洞后，一般情况下滑裂面的抗滑安全系数是提高的，但传力洞的半径不同，其对滑裂面增稳的幅度不同，而且增稳幅度并不一定随着传力洞半径增大而单调递增.

根据抗滑安全计算公式(1)和(2)，影响安全系数的指标主要是滑裂面上的正应力σi和剪应力τi，设置了传力洞以后，拱坝传至坝肩的推力，部分由传力洞承担，传至滑面之后的坚固岩体，因此在传力洞影响范围内，滑裂面上的正应力分量和剪应力分量是同时减少的.当改变传力洞的半径后，传力洞刚度相应改变，其承担的坝肩推力也改变.当传力洞的刚度太大时，坝肩推力大部分由传力洞承担，又由于特定的传力洞方向，导致滑面上的正应力很小，就会出现传力洞半径增大而滑面抗滑安全系数不随之增大的情况.这一点从图4～图8中滑裂面在传力洞附近点(3～7号点)的抗滑安全系数变化规律也可以看出，当传力洞半径达到3.0 m时，这几个点的安全系数反而降低.

3 结 论

传力洞对处理拱坝软弱破碎带基础具有较好的效果，实际工程中应用也很普遍.本文分析了不同半径传力洞对特定滑裂面抗滑稳定安全系数的影响.结果表明，传力洞的设置对软弱破碎带内的特定滑裂面抗滑安全通常是有利的，但当传力洞半径设置不当时，也有可能反而不利于滑裂面的抗滑稳定，这一点在实际工程的设计中应该引起重视.

[1] 李 瓒，陈兴华，王光纶，等.混凝土拱坝设计[M].北京：中国电力出版社，2000.

[2] 赵炳祯，郑建波，冯树祥，等.黄河龙羊峡水电站重力拱坝基础处理设计[J].西北水利发电，1986(2)：6-16.

[3] 刘 健，谢新生，王 旭.基础约束对拱坝应力影响规律的研究[J].西北水电，2009(1):58-60.

[4] 王清亮，唐辉明，胡丽新.地基变形模量对碾压混凝土拱坝应力分布的影响[J].地球科学(中国地质大学学报)，2007(3):409-414.

[5] 杨保全,陈 媛,张 林,等.基于地质力学模型试验的锦屏拱坝坝肩加固效果研究[J].岩土力学，2015(3):819-826.

[6] 苏卫强,吴志波,何 力.复杂地质条件下拱坝坝肩抗滑稳定分析及处理研究[J].水利水电技术，2015(3):61-64.

[7] RANDOLPH M F, WROTH C P. Analysis of Vertical Deformation of Pile Groups[J]. Geotechnique, 1979,29(4):423-439.

[8] 杨庚鑫,陈建叶,张 杨，等.混凝土传力抗剪结构在拱坝坝肩加固处理中的效果分析[J].四川大学学报(工程科学版)，2013(5):34-39.

[9] 徐卫亚,倪海江,狄圣杰，等.白鹤滩水电站坝基加固方案评价[J].水力发电学报，2015(3):129-136.

[10] 陈英儒，杨 强，包劲清.高拱坝坝基断层加固力研究[J].水力发电学报，2008，27(6):62-67.

[11] 吴党中，刘国华.拱坝基础处理中的传力洞设计[J].河海大学学报(自然科学版)，2010，38(6):711-715.

Effect of Concrete Plug Section on Abutment Stability of Arch Dam

WU Dang-zhong1, WANG Mao-rong2
(1.Zhejiang Zhongshui Engineering Technology Co., Ltd, Hangzhou 310020, China; 2.Zhejiang College of Construction, Hangzhou 311321, China)

Concrete plug has a good effect on the treatment of soft fracture zone of arch dams, and it is also widely used in practical engineering. The three-dimensional finite element model of arch dam and its foundation is modeled, and the influence of concrete plugs with different semidiameter on anti-sliding stability of specific sliding surface in soft foundation is also analyzed. The results show that the setting of concrete plugs is often beneficial to the specific sliding surface in soft fracture zone, but when the semidiameter of the concrete plugs is not suitable, there may be disadvantageous to sliding stability, as an added note.

dam foundation treatment; concrete plug; fault fracture zone; limited element

2016-09-26

吴党中(1978-)，男，江西东乡人，博士，高级工程师，主要从事水电站设计和水工建筑物加固工作.

TV642.4

A

1008-536X(2017)02-0029-04