深水钻井立管建模与角度安全控制
王 芳,白 勇,徐 锋
(1. 杭州电子科技大学 机械工程学院,浙江 杭州 310018;2. 浙江大学 建筑工程学院,浙江 杭州 310058;3. 武汉第二船舶设计研究所,湖北 武汉 430064)
深水钻井立管建模与角度安全控制
王 芳1,白 勇2,徐 锋3
(1. 杭州电子科技大学 机械工程学院,浙江 杭州 310018;2. 浙江大学 建筑工程学院,浙江 杭州 310058;3. 武汉第二船舶设计研究所,湖北 武汉 430064)
从水面钻井平台与水下立管联合作业的安全角度出发,提出一种将钻井立管的力学响应限制特性引入水面平台动力定位闭环控制中的位置保持方法,实现水面钻井平台(或船舶)基于立管角度响应的动态定位。利用有限元方法建立包括立管系统质量、系统刚度、结构阻尼和水动力载荷在内的立管运动控制模型。联合水面浮体和水下立管的低频运动特性建立水面浮体运动偏移与水下立管顶端角度及末端角度的相对运动关系模型。在此基础上,设计基于立管运行响应的动力定位控位方法,实现对立管顶端角度及末端角度的安全控制。仿真结果表明,所提出的方法可行,在外界突变的环境载荷瞬时作用于水面浮体时,能更快地跟踪新的期望最优位置,保证钻井立管运行在安全界限内。
动力定位;位置保持;钻井立管;钻井平台
0 引 言
深水浮式结构物在深海油气资源勘探方面有着不可或缺的作用。作为深海油气资源开发必备的关键技术,合理而准确地控位是各类海洋工程船舶和平台在海上安全作业的前提,直接关乎海上钻井、修井、铺管及补给支持等作业的安全与成败。无论是近海的系泊定位[1],还是深海的动力定位[2-3],水面浮式结构物控位的根本目的都是保证连接水下井口与水面浮体的钻井立管或生产立管的各运行参数在安全范围内,使海上钻井及修井等作业安全、持续进行。随着油气资源开发不断向深海拓展,钻井立管入水深度将达到千米级,使钻井立管在未知的深海环境中保持正常的形态和应力载荷是各类海上移动式钻井装置在深海作业面临的一大挑战[4]。
目前使深水钻井立管顶端接头处角度及海底井口端接头处角度保持在安全范围内的途径主要有提升顶端张紧力[5]和通过系泊或动力定位实现控位[6-8]2种。
1) 提升立管顶端的张紧力虽然可减少立管的变形及立管顶端接头处和末端接头处的角度偏移,但会导致立管水下部分承受较大的应力,这对立管的强度或材料提出更高的要求,会使作业成本大幅度提高。此外,该方法只能应对流载荷引起的较小角度的偏移,无法应对浮体运动引发的较大角度的偏移,且立管顶部张紧力的提升有最大值的限制。
2) 控位主要依靠系泊或动力定位来调整浮体的运动或位置,进而减小立管顶端接头处和末端接头处的角度偏移。
(1) 由于系泊系统不能准确控制浮式结构物在某个自由度上的运动或位移,因此根据作业海域的环境条件和气候特征预先布置锚索,从宏观上对主导风浪或海流的作用力进行阻尼抑制;
(2) 动力定位作为一种主动式定位方式,不受海洋结构物工作水深的限制,分别对浮式结构物水平面的纵荡、横荡及艏摇等3个自由度的运动实施控制,通过控制算法对水面浮体低频运动作出响应。
因此,通过动力定位主动控位实现钻井立管顶端接头处角度和末端接头处角度在深水区域的安全控制是目前较为可行的途径。然而,已有的动力定位控制算法均未具体考虑立管运行参数的安全域,只是将浮体尽可能地保持在海底井口上方,而浮体最优位置通常是人工设定的,随着海洋结构物作业水深不断增加,操作员将很难对最优位置进行判定。鉴于目前钻井船舶或钻井平台上均配备有监测立管角度的传感器,在对立管进行数学建模的基础上将立管的主要运动响应因素引入动力定位闭环控制研究中,根据水面浮体与水下立管相对运动的函数关系,引入立管运动参数与定位精度指标,设计动力定位最优控制目标函数,运用最优化理论进行建模和求解。
1 钻井立管安全工作要求
依靠动力定位实现控位的海洋钻井平台在深海区域进行钻探作业时,主要依靠自身的推力器系统产生抵抗外界环境载荷(风、海流、波浪)所需的力和力矩,从而使其自身保持在特定的作业区域(见图1)。理想情况下,钻井平台应在绿色线区域内进行钻探作业,此时钻井立管在水面浮体端及海底井口端的角度保持在安全限制范围内;若钻井平台因发生较为严重的移位而进入黄色线区域,则钻探作业必须停止,相关人员准备启动紧急断开程序[9];若钻井平台进入红色线区域,则紧急断开程序被触发;若未能在钻井平台移出红色区域前断开钻井立管与海底防喷器组的连接并关闭井口,则可能导致立管、放喷器组及井口被损坏,甚至出现井喷等重大事故。根据美国石油协会(American Petroleum Institute,API)的规定[10]:
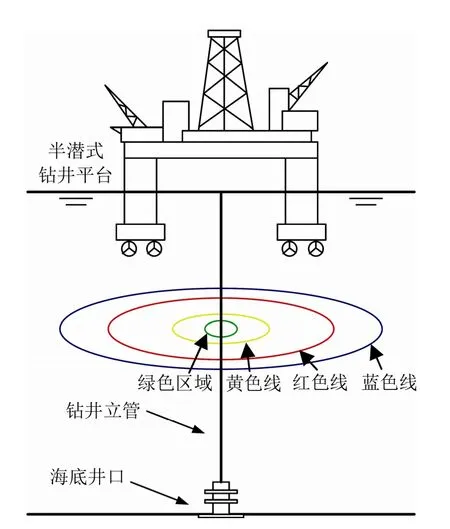
图1 深水钻井平台作业区域示意
1) 连接钻探时,钻井立管顶端接头处角度tα的平均值<2°,最大值<4°;海底井口端接头处角度bα的平均值<1°,最大值<4°;
2) 非连接钻探时,钻井立管顶端接头处角度tα的最大值<9°;海底井口端接头处角度bα的最大值<9°。
2 深水钻井立管运动建模
钻井立管在作业时通常被简化为一根横向受力的垂向长梁。其顶端受张紧力的作用,有效张力沿管长分布于整根立管,并跟随水面浮体运动;底端被视为与海底井口端固定;侧面主要受海流载荷的作用。这里只考虑立管的二维运动,记在大地坐标系下的EEX Z平面内立管顶端接头处的角度为tα,底端接头处的角度为bα。为获得立管顶端接头处和末端接头处的角度值,采用有限元(FEM)方法对其进行离散化处理[11]。图2为钻井立管离散节点与单元示意,将立管离散为n个单元(n+1个节点),海底底端为第1个节点,水面浮体为第n+1个节点,顶端张紧力作用在第n+1个节点上。在立管运动坐标系下,定义节点i在RX 轴方向和RY轴方向上的位置分别为ix及iz,各单元的倾角可表示为

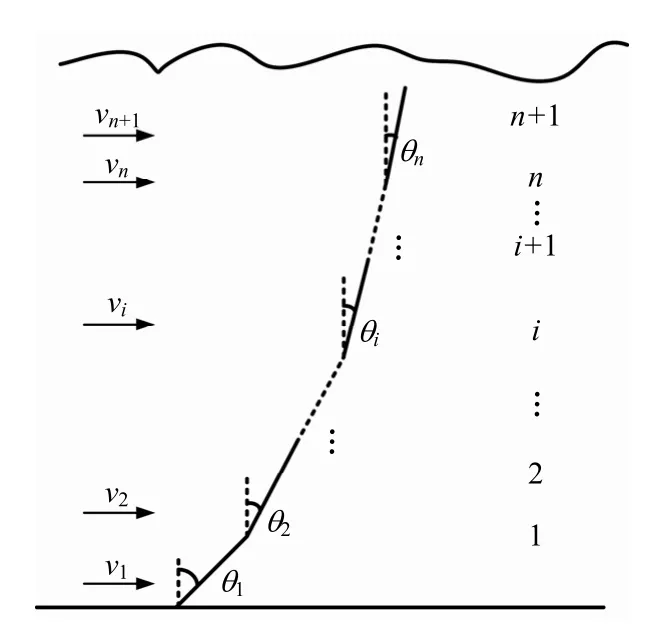
图2 钻井立管离散节点与单元示意
由此,立管的每个单元对应2个节点,每个节点对应2个自由度,则大地坐标系下整根立管的位置向量可表示为

由于只考虑立管的二维运动情况,即只考虑水面浮体的纵荡运动对立管角度的影响,而大地坐标系的x轴方向与海底固定坐标系的x轴方向一致,因此立管局部坐标系下的位置与海底固定坐标系或大地固定坐标系下的位置的相互转换均通过式(3)完成。

若只考虑二维情况,忽略y轴方向的位移,则可得二维转换矩阵为

对应每个单元立管的转换矩阵为

2.1 立管系统质量矩阵
每个立管单元的质量矩阵均由立管的结构质量、惯性流体质量及附加质量组成,即


在局部坐标系下,立管单元的结构质量矩阵表示为式(7)中:sρ为立管材料密度;A为立管的横截面积;il为立管单元的长度;fρ为立管内部液体的密度;intA为立管的内截面面积;wρ 为立管外部流体的密度;eA为立管的外截面面积;mC 为附加质量系数。
根据式(5),将局部坐标系下的立管单元质量矩阵转换到大地坐标系下,可得

最后可得钻井立管在大地坐标系下的系统质量矩阵为

2.2 立管系统刚度矩阵
在局部坐标系下,单元立管的刚度矩阵由弹性刚度Eik 和几何刚度Gik 组成,即

式(10)中:E为立管的杨氏模量;iP为单元立管的有效张力,为无外力作用下立管单元的初始长度;il为外力作用下立管单元的实际长度,
根据式(5)对局部坐标系下的单位立管刚度矩阵进行转换,最终得到大地坐标系下整根立管的刚度矩阵为

2.3 结构阻尼力
立管所遭受的阻尼力包括结构阻尼力和水动力阻尼力,其中,结构阻尼力相对较小,水动力阻尼力在载荷建模中考虑。这里只考虑立管的结构阻尼力,近似采用Rayleigh阻尼模型来表示,即

式(12)中:系数1a和2a可通过引入阻尼比率nξ与频率nω的函数关系式来求解,即

由于同一个阻尼比率通常对应系统的2种频率(nω和mω),因此1a和2a的计算式可简化为

2.4 水动力载荷
深水钻井立管遭受到的载荷主要来自于水面浮体的运动及水动力载荷(主要为海流载荷),运用改进Morison方程计算单位管长的水动力载荷为

式(15)中:wv和wv˙为水质点的速度与加速度;r˙和r˙˙为水面浮体的运动速度与加速度;dC为阻力系数;mC为惯性系数;outD 为立管外径。由于附加质量的影响已在系统质量矩阵中予以考虑,同时波浪诱导运动在深水中不予考虑,因此式(15)中只有第1项考虑海流与水面浮体运动影响的拖曳阻尼,最终单位管长的水动力载荷hf表示为

沿管长方向对单位管长的水动力载荷进行积分,可得该单元所承受的水动力载荷;同理,经过坐标转换,可得整个立管在大地坐标系下的水动力载荷向量hydroF 。
综上,通过有限元离散分析求得立管的系统质量矩阵、刚度矩阵、结构阻尼矩阵及水动力载荷,最终可得整根立管的运动方程为

由于立管第1个节点与第n+1个节点的约束条件部分已知,即第1个节点固定于海底,第n+1个节点x方向上的位移为水面浮体的纵向位移,因此将这些已知节点在矩阵中对应的行与立管的位置列向量相乘得到的项移到式(17)等号右边作为水面浮体运动的影响可得立管所有自由节点的运动方程为式(18)中:
3 立管角度安全控位方法
根据以往海上移动钻井设施动力定位的经验,水面浮体的期望位置dη并未考虑水下立管顶端接头处和末端接头处的角度响应,始终保持在海底井口上方。这里提出的控制方法将钻井作业的2个重要运行参数(即立管在水面浮体端及海底井口端的角度响应)在动力定位控位循环中予以考虑。由已推导出的考虑水面浮体运动的立管模型可知,钻井立管的运动响应主要受浮体的运动和海洋环境载荷(主要是海流载荷)的影响。文献[12]指出,若立管运动的固有频率远不在水面浮体的低频运动范围内,则立管模型中的惯性项和动态阻尼项可忽略。由于式(17)只考虑刚度项,因此可近似假设立管在每个控制节拍内的位移增量 rΔ与水面浮体在水平面的位移增量vesselrΔ 在一定的海流条件下线性相关,立管角度控制模型可表示为
由此,立管顶端接头处和末端接头处角度增量的变化[12]可表示为

式(20)中:系数txc,txc,bxc ,byc 可通过有限元分析计算得到;ndof为自由节点的自由度数。
为使立管顶端角度和末端角度维持在立管安全运行范围内,定义关于立管角度的代价函数为

式(21)中:tw和bw分别为立管顶端角度及末端角度的权重系数。
通过对代价函数求水面浮体位移增量分量的一次导数,可得到使代价函数最小的水面浮体位移增量分量为

若海流与水面浮体的运动仅发生在xOz平面且沿着Ox方向,则最优增量位移的方向为0°,水面浮体最优增量位移为

水面浮体最优的期望位置最终表示为

4 仿真试验
为验证所提方法的有效性,以“海洋石油981”深水钻井平台为研究对象进行动态模拟仿真[13]。仿真中,钻井立管的长度为1500m,立管外径为0.25m,管壁厚度为0.025m,杨氏模量E=2.1×105MPa,顶部张力为2500kN,立管在长度方向上被离散为10个单元。钻井立管主要遭受的海洋环境载荷为海流载荷,海流载荷随水深的分布情况见表1,其中 Vc= 0.93m/s 为钻井平台作业工况下遭受的海流平均速度值。钻井平台作业工况下的系统矩阵参数为
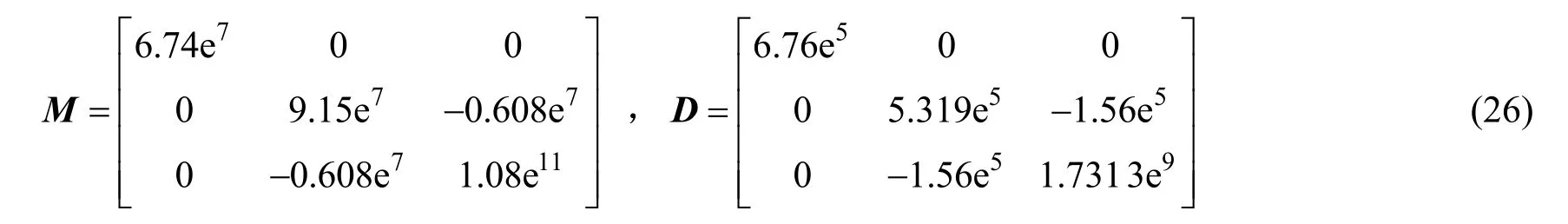

表1 深海钻井立管的海流载荷随水深的分布情况
仿真时,立管顶端角度和末端角度控制选取为相同的权值,即tw=b1.0w= 。在作业工况下,风载荷的平均速度为23.2m/s,方向为0°。海洋钻井平台水平北向的位移和水平东向的位移见图3及图4。
由试验结果可知:
1) 由于海洋平台最优位置的选取考虑钻井立管顶端接头处和末端接头处的角度响应,因此期望位置点不是永远保持在井口上方的(0m,0m)点,而是根据当前海况综合考虑钻井立管顶端接头处和末端接头处角度的安全限值动态地变化着。
2) 当海洋钻井平台突然遭受风载荷时,风前馈控制器会及时抵消一部分风载荷的影响,同时以最小化立管顶端接头处和末端接头处角度为目标的平台期望位置将发挥作用,使海洋平台不断地向着能保证立管在当前海况下持续安全运行的区域运动,尽量控制立管顶端接头处和末端接头处的角度值在安全范围内。北向最大偏差在2.5m左右,东向最大偏差在1.0m左右。

图3 钻井平台北向位移
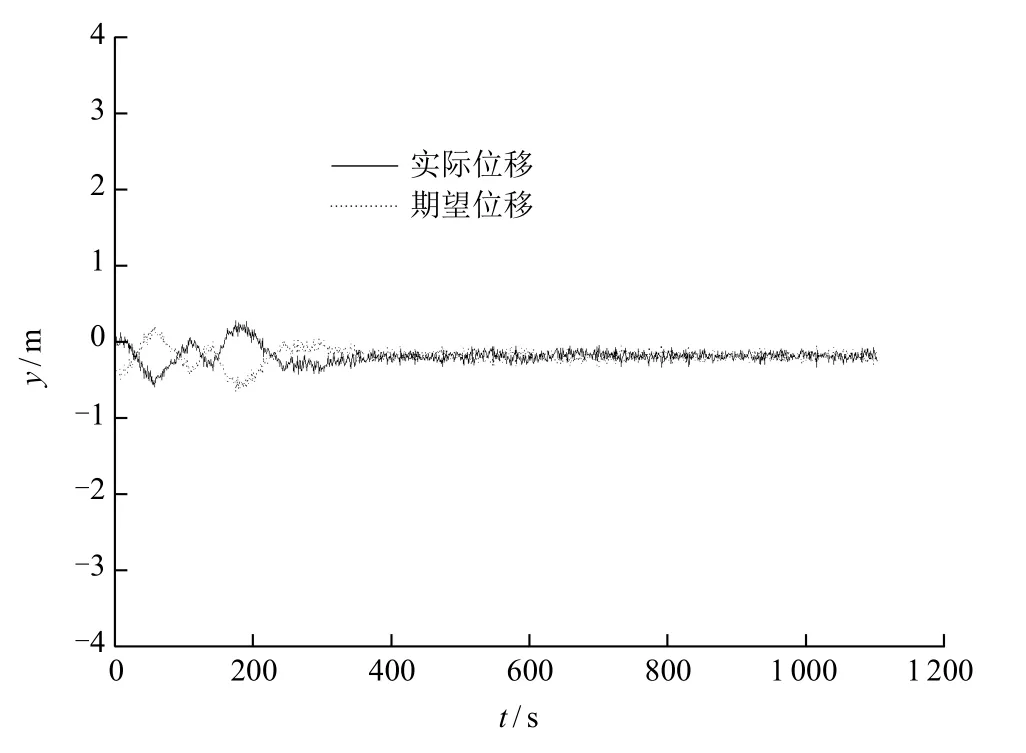
图4 钻井平台东向位移
钻井立管顶端接头处和末端接头处角度值的时历响应见图5~图7。立管顶端接头处角度分量txα 和tyα分别为立管顶端角度在xOz平面及yOz平面的投影角度;立管末端接头处角度分量bxα 和byα 分别为立管末端角度在xOz平面及yOz平面的投影角度。立管顶端接头处和末端接头处最终合成角度的大小取为

图5 钻井立管顶端角度时历响应

图6 钻井立管末端角度时历响应
由试验结果可知:当风载荷开始作用于水面浮体时,立管顶端角度和末端角度均发生较大幅度的偏移,由于风的作用方向为0o,因此txα 和bxα 的偏移较tyα 和 αby大,αtx和 αbx分别在风载荷开始作用于水面浮体时出现一个偏移峰值。通过数据分析得到当前海况下立管在顶端和底端柔性接头处的转角的平均值与最大值(见表2和表3),最终αt与 αb的平均值均小于API规定的安全限值。

图7 钻井立管顶端角度和末端角度时历响应

表2 立管顶端接头处角度

表3 立管底端接头处角度
为对比不同方法的控制效果,进行仿真对比试验。所采用的对比控制方法不考虑水下钻井立管的角度响应,水面钻井平台的期望位置始终保持在井口上方,设为(0m,0m)点。采用上述环境载荷加载条件和权值设置条件,得到对比试验的结果(见图8和图9)。

图8 对比控制下的北向位移

图9 对比控制下的东向位移
由对比试验结果可知:
1) 在外界瞬时载荷突然作用时(风载荷在180s左右加载),考虑立管角度响应的控位方法能比传统不考虑立管角度响应的控制方法更快地跟踪新的期望最优位置,控制效果较好。
2) 由于风载荷在0°方向加载,因此浮体北向的位置偏差较东向大,最大北向瞬时偏差约为2.8m,最大东向瞬时偏差约为0.5m,控位偏差比不考虑角度响应的控位方法要小。
3) 不考虑立管角度响应的传统控制方法始终以井口正上方为固定期望位置,实质上要求浮体始终跟踪一个全局静态最优点,未考虑浮体当前遭受的瞬时或稳态环境载荷,不同的环境载荷配置对立管角度响应具有不同的影响。对于推进器系统而言,全局最优点不一定可达(跟踪),而考虑钻井立管角度响应的动态局部最优点既可减少当前海洋环境条件下推进器系统的不必要磨损,又能保证立管各运行参数控制在安全界限内。
5 结 语
本文对考虑钻井立管角度响应的动力定位控位方法进行研究。结合不同控位方式的特性对水面钻井平台和水下钻井立管安全作业要求进行分析,结果表明,通过动力定位模式控制水下钻井立管顶端角度和末端角度更为可行。通过对水面浮体和水下立管进行运动建模,得出两者相对运动的影响关系,特别是水面浮体的纵荡运动、横荡运动及位移对立管角度的影响。在动力定位模式下,以最小化立管角度为目标,结合当前海况,对浮体最优期望位置实现动态寻优和定位,以此代替以往不考虑立管状态的固定期望位置点。仿真试验结果表明,所提出的方法是有效的;通过与已有方法相比较,证明了该方法的优越性。将立管角度的实时响应定量引入到动力定位的闭环控制中,可有的放矢地提升主动定位的精度和性能,为深海高精度控位模式与方法研究提供新的思路。下一步将开展模型试验研究,进一步验证其有效性。
[1] 金鸿章,苏晓宇,于安,等. 基于锚链切换的平台自动锚泊定位系统设计[J]. 电机与控制学报,2014, 18 (5)∶ 93-98.
[2] 马刚,孙丽萍. 基于总体坐标法的大变形锚泊线的静力分析[J]. 哈尔滨工程大学学报(英文版),2014, 35 (6)∶ 674-478.
[3] FOSSEN T I. Marine control systems∶ guidance, navigation and control of ships, rigs and underwater vehicles[M]. Trondheim, Norway∶ Marine Cybernetics AS, 2002∶ 100-121.
[4] 边信黔,付明玉,王元慧. 船舶动力定位[M]. 北京:科学出版社,2011∶ 20-30.
[5] RUSTAD A M, LARSEN C M, SORENSEN A J. FEM modeling and automatic control for collision prevention of top tensioned riser[J]. Marine Structures, 2007, 21 (1)∶ 80-112.
[6] DO K D, PAN J. Boundary control of three-dimensional inextensible marine riser[J]. Journal of Sound and Vibration, 2009, 327∶558-571.
[7] SUZUKI H, WATANEBE K, YOSHID K. Operability improvement of deepsea riser by active control[C]. In Proceedings of OMAE’95, 14th International Conference on Offshore Mechanics and Arctic Engineering, 1995∶ 289-297.
[8] NGUYEN D H, NGUYEN D T, QUEK S T, et al. Control of marine riser end angles by position mooring[J]. Control Engineering Practice, 2010, 18∶ 1013-1021.
[9] 白勇,戴伟,孙丽萍,等. 海洋立管设计[M]. 哈尔滨:哈尔滨工程大学出版社,2014∶ 193-210.
[10] American Petroleum Institute. Recommended practice for design and analysis of station keeping systems for floating structures[S]. 2nd ed. API Recommended Practice 2SK, 1996.
[11] DAI W, GAO F, BAI Y. FEM analysis of deepwater drilling risers under the operability and hang-off working conditions[J]. Journal of Marine Science and Application. 2009, 8∶ 156-162.
[12] LEIRA B J, CHEN Q F, SORENSEN A, et al. Modeling of riser response for DP control[C]. Proceedings of OMAE’01, 20th International Conference on Offshore Mechanics and Arctic Engineering, 2001∶ 1-9.
[13] 王芳,万磊,姜大鹏,等. 基于Vxworks的DP-3动力定位控制系统设计与分析[J]. 上海交通大学学报,2012, 46 (2)∶ 217-223.
Modeling and Safety Control of Deepwater Drilling Riser Angles
WANG Fang1,BAI Yong2,XU Feng3
(1. School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, China; 2. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China; 3. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China)
From the aspect of safe operation in collaboration with the drilling platform above the water and the risers beneath, this study proposes a station keeping method which considers the mechanical response constraints of the drilling risers in the dynamic positioning close-loop control, so as to achieve the dynamic positioning of the surface drilling vessel or platform based on the riser angle responses. A control model is established for riser motion with finite element method, which includes riser system mass, system stiffness, structure damping and hydrodynamic loads. The relative motion model between the movement of the surface floating body and the top and end angles of the underwater riser is established depending on their low frequency motion characteristics. In this way, the dynamic positioning control method is designed according to the riser motion response, and the safety control of the top and end angles of the risers is realized. Simulation result shows that the proposed method is feasible. The surface floating body can track the new expected optimal position more rapidly in case there are transient external environmental loads, and thus to ensure the riser operation within safety limits.
dynamic positioning; station keeping; drilling riser; drilling platform
P756.5;U674.38+1
A
2095-4069 (2017) 02-0010-08
10.14056/j.cnki.naoe.2017.02.002
2016-07-14
国家自然科学基金(51509193);浙江省自然科学基金(LQ15E090007)
王芳,女,讲师,1985年生。2012年毕业于哈尔滨工程大学船舶与海洋结构物设计制造专业,主要从事深海浮式结构物动力定位技术研究。

