基于扩展Petri网的飞机装配系统设备调度方法*

（南京理工大学机械工程学院，南京 210094）

飞机零部件数量较多且装配过程复杂，涉及设备资源较多，有效的建模方法和设备调度优化策略能够很好地缩短生产周期并降低成本。目前对于飞机装配建模方法的研究主要包括Petri网、面向对象、排队网络、事件驱动链[1-4]等。文献[5]提出了基于面向对象的复杂产品装配建模方法，描述了装配过程中的主要对象类及其关系；张杰等[6]以Petri网为基础，探讨了飞机装配系统层次化建模方法，并进行锁死分析，但Petri网存在组合爆炸问题需要改进；徐开元等[7]探讨了飞机分层装配线、装配资源模型的构建。但是，上述研究更多注重装配线流程及布局的改善，涉及飞机装配设备调度优化方面较少。

基于此，本文根据飞机装配工艺利用面向对象Petri网（Object-Oriented Petri Nets，OOPN）建立飞机装配模型并构建装配元逻辑关系，将模型高度抽象化模块化[8]。在OOPN装配模型基础上以赋时Petri网（Timed Petri Nets，TPN）构建并扩展装配元-装配设备-体化模型，形成扩展Petri网（Object-Oriented Timed Petri Nets，OTPN），并以装配元变迁为基础，嵌入混合算法用以解决装配元设备调度优化问题。

1 OTPN定义

1.1 OOPN模型定义

OOPN建模的基本构造是对象，对象将数据结构与行为集成为一个相对独立的实体，可表示为S={Ob,R}，此方法能够抽象化、模块化装配单元，且易于理解。其中Ob为系统的对象集合；R为系统中对象的关系集合。Obi和Rij分别定义为：

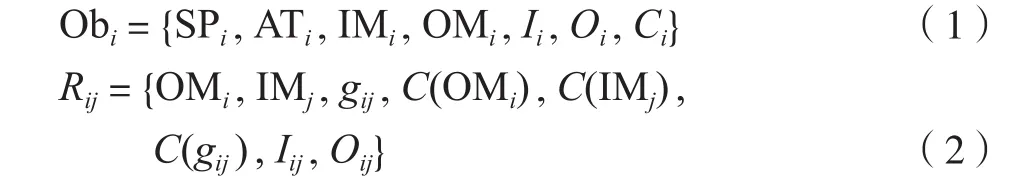
式中，SPi表示Obi状态库所的集合；ATi表示Obi活动变迁的集合；IMi表示Obi输入信息库所的集合；OMi表示Obi输出信息库所的集合； Ii为输入映射；Oi为输出映射；Ci为颜色集；gij表示从Obi到Obj的信息传递的门的集合；Iij表示从OMi到gij的弧集，理解为输入函数；Oij表示从gij到IMj的弧集，理解为输出函数。

飞机装配OOPN模型构建主要包括元对象模型构建和逻辑对象模型构建。元对象是指装配系统中可模块化的作业实体映射到OOPN中的模型对象，分为装配功能元对象与辅助装配元对象。元对象模型构建主要包括内部框架（OPN）与信息协议（OMP）两部分内容，模型构建方法如下：

步骤1：按照飞机装配工艺对模型进行层次划分；

步骤2：将飞机装配工序转换为OPN变迁序列；

步骤3：变迁序列中融入库所，形成状态库所集；

步骤4：将装配作业资源赋予相应工序变迁，形成资源库所集合；

步骤5：连接内部变迁与库所，形成OPN模型；

步骤6：建立各个逻辑门Gi，整合元对象的IMi和OMi形成 OMP；

步骤7：依据门变迁和关系集，对元对象的进一步组合形成逻辑对象，如图1所示；

步骤8：建立初始标识Mo，表示出所有库所的初始标识。

1.2 OTPN模型构建

TPN是在基本Petri网中融入时间因素，可用于描述含有时间因子的制造系统模型，对于设备调度有着较好的指导意义，定义为TP=（P,T），其中P为基本Petri网，T为变迁ti的时间集合。

实际飞机装配OOPN模型中设备资源的使用冲突分为两类：多个装配单元请求同一设备；某个装配变迁的完成可有多种设备选择方案。为此首先建立装配元-装配设备关系表，用来描述各个装配元可以由哪些设备来完成，以及设备在完成装配的时间，如表1所示。

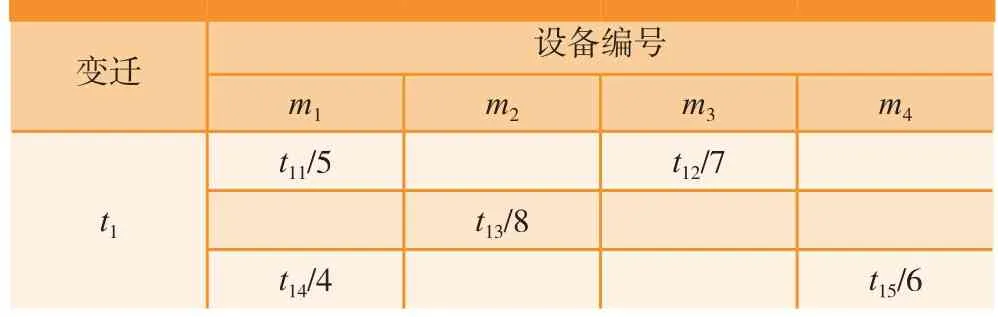
表1 装配元-装配设备关系表

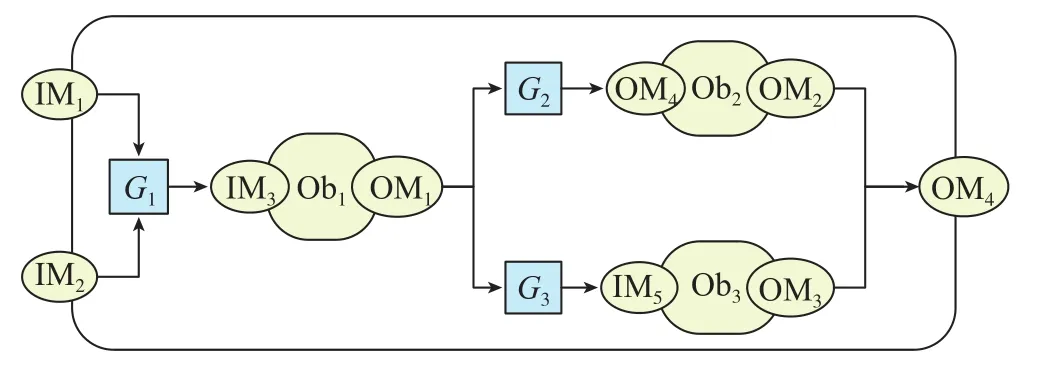
图1 逻辑对象Fig.1 Logical objects

表 1 中，t1表示装配变迁，m1、m2、m3、m4表示设备，从表1可得装配变迁有3种设备选择方案，第一种方案m1设备耗时5个工时，m3耗时7个工时。

利用装配元-装配设备关系表对装配元变迁进行扩展并建立设备选择库所集，形成变迁TPN模型。模型包括的信息为设备配置方案（见表1），库所与配置方案相对应。实际装配过程中，只有一种设备配置方案被选中，故库所集中只有一个库所托肯数是1。

将变迁TPN模型整合融入飞机装配OOPN模型中形成OTPN模型，图2表示对装配元变迁t1扩展形成的OTPN模型。

2 混合算法设计

设备调度涉及因素较多，属于典型的NP问题[9]。依据OTPN模型中的装配元变迁序列及其设备库所选择集，在遗传算法中（Genetic Algorithm，GA）引入模拟退火算法（Simulated annealing Algorithm，SA），从选择库所集中选择最佳配置方案，进而提高设备利用率，减少装配时间，算法流程如图3所示。

混合算法从算法机制、结构、操作等方面融合了单一算法的缺点，能够扩充全局空间并增大搜索能力，有效克服初值依赖性、过早收敛等缺陷，同时引入自适应交叉和变异概率，使算法在优化过程中避免盲目交叉从而提高搜索效率[10-11]。

2.1 染色体编码

编码是将飞机装配系统中的设备使用顺序依照装配元变迁映射到染色体上。从每个装配元的多个配置方案中选择一个作为基因，所有被选择的配置方案按序排列，形成一条染色体。

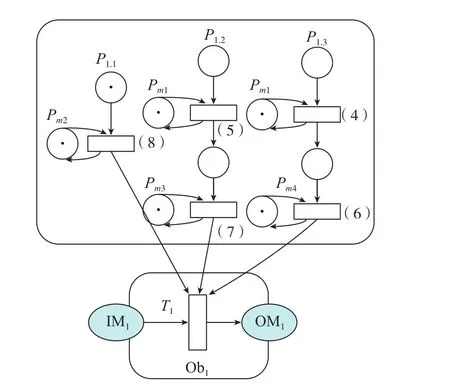
图2 装配元变迁OTPN模型Fig.2 OTPN model of assembly element transition

2.2 适应度函数

本文以装配元装配完成时间和辅助设备利用率为优化目标。装配时间指的是以选定的设备配置方案配置装配元进行装配操作，完成A-OOPN模型中所有装配的时间。设备利用率UT是指设备实际工作时间与全部工作时间的比值，是一个随时间变化的离散统计量，定义为：

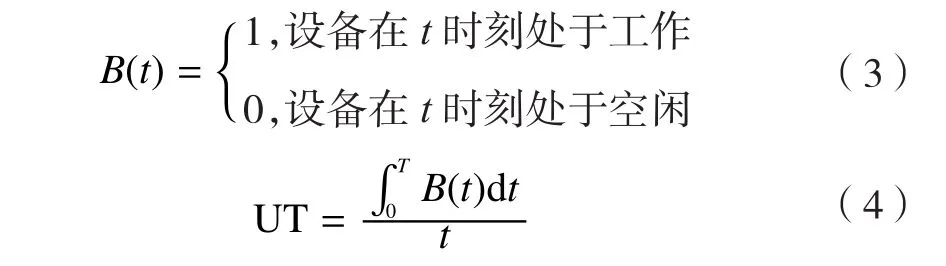
式中，B（t）代表工作时间，t代表时刻。

2.3 选择算子

选择操作用于优胜劣汰，这里选用轮盘赌的方法，即每个个体被选中的概率与适应度函数值的大小成比例关系。设种群大小为N，个体xi适应度为f(xi)，则个体xi被选中的概率为：

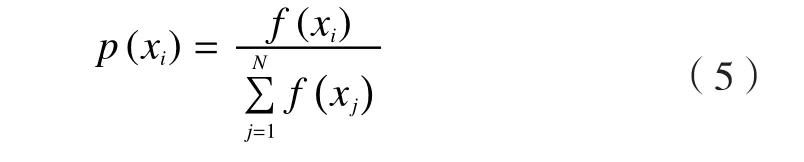
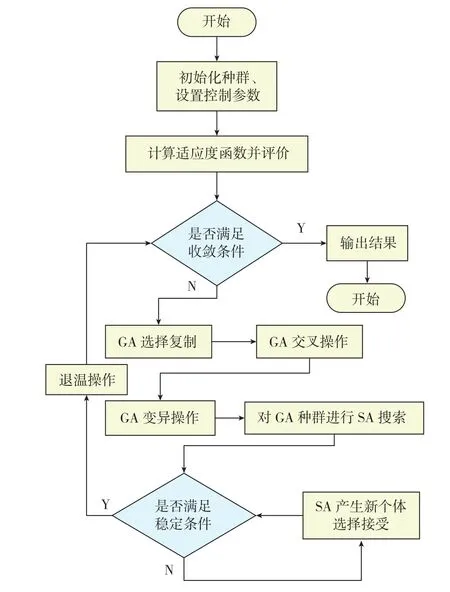
图3 混合算法流程Fig.3 Flow of hybrid algorithm

2.4 模拟退火算法规划

为避免过早收敛，在GA中引入SA，运用Metropolis准则判断是否产生并选择新的个体。Metropolis准则依照公式（6）对经过GA算法的新个体进行筛选，具体公式如下：

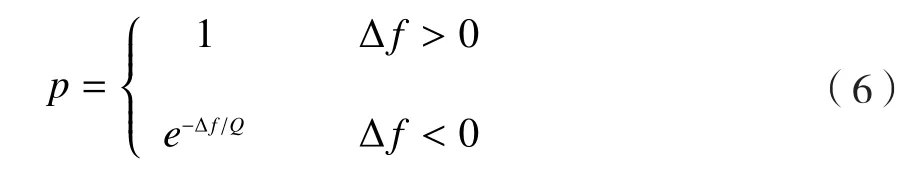
式中，Q表示SA温度；Δf表示当前新个体与原个体适应度值之差，若Δf＞0，则以概率1接受更好的个体。将当前最优解与下一代比较并进行退温操作Qk=aQk-1，再返回遗传算法直至满足终止迭代条件。SA中的初始温度值越大，获得优秀解的概率越大，但所需运算时间也越长，所以初温设置从运算效率与优化效果两方面进行考虑。

3 实例应用与分析

机身装配涵盖了飞机装配的众多特性，如串行装配和并行装配等，是脉动生产线的重要环节。论文以某型号飞机中机身装配过程为对象，建立OTPN模型并对装配设备进行调度优化，由于其并行装配为主，故存在众多设备资源的竞争使用。中机身装配元信息见表2。

装配元涉及的公共资源有4个，1个输送平台m1，2套工业夹具m2和m3，1辆小车m4。装配顺序及其设备关系如表 3 所示，装配元变迁T={T11，T12，T13，T14，T15，T16，T17，T18}对应表 3 中装配 {1，2，3，4，5,6，7，8}。

表2 中机身装配元信息

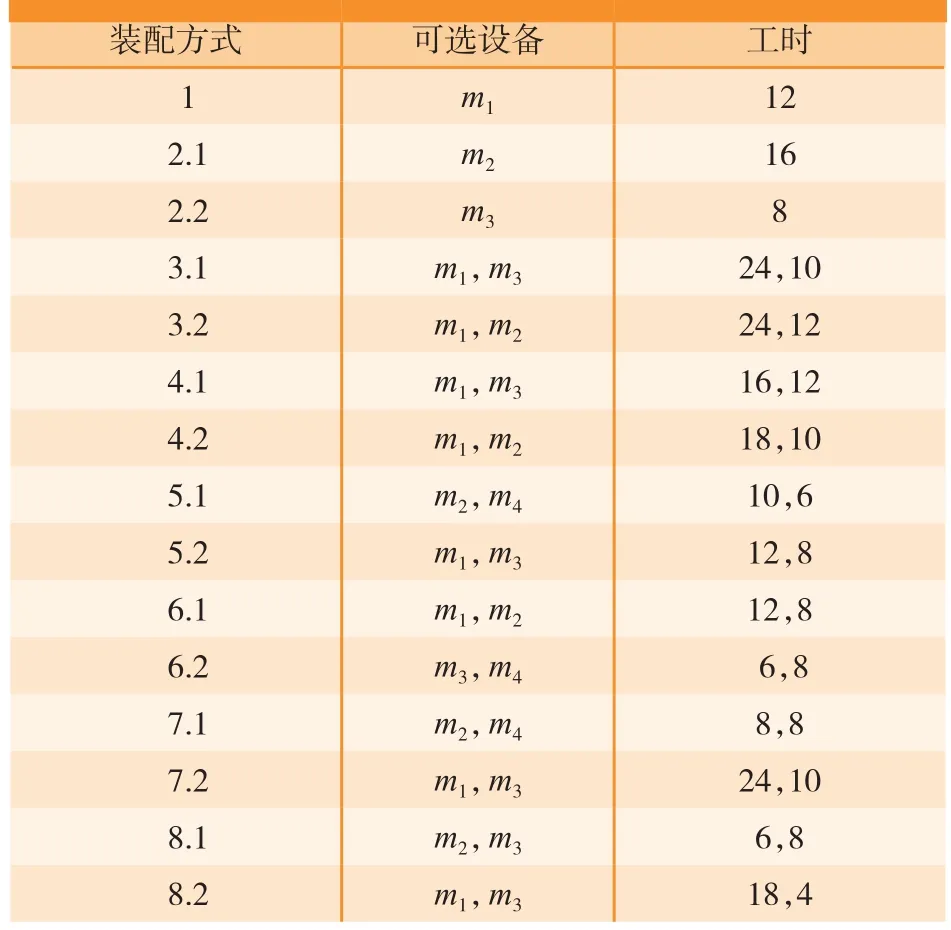
表3 装配设备关系表

表3中每个装配可能有多个选择，例如装配2有两种配置方案，分别是方案2.1和2.2。中机身OTPN模型如图4所示。

为保证群体多样性及进化能力，在计算量许可情况下，混合算法参数设计如下：种群个体数目N为80个，代沟G为0.9，交叉概率Pc为0.9，变异概率Pm为0.05，进化代数100，模拟退火冷却系数q为0.9，终止温度Tend为0.001℃，退温次数为50。以上面参数为依据，以MATLAB为工具计算分析，算法求解收敛曲线如图5所示。

从图5中可发现，算法经过50代完成运算求解过程。与单一算法相比较，混合算法收敛较为平缓，相对GA算法避免了早熟，相对SA算法能控制求解方向并进行全局搜索，且具有较快的搜索效率。

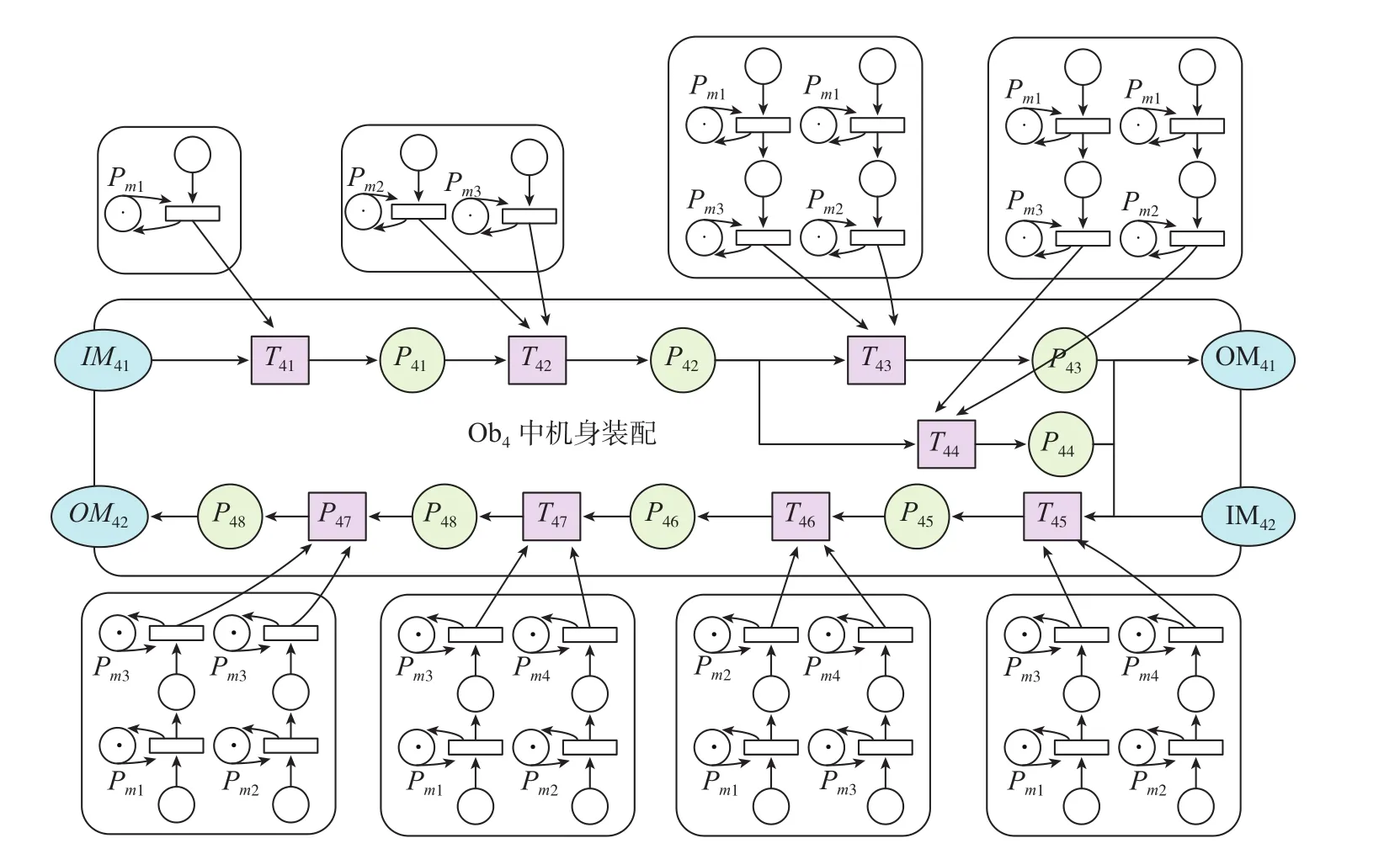
图4 中机身OTPN模型Fig.4 Fuselage OTPN model

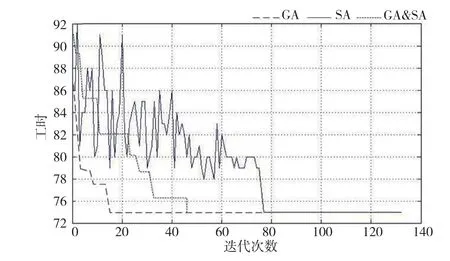
图5 混合算法求解收敛曲线Fig.5 Convergence curve of hybrid algorithm solving

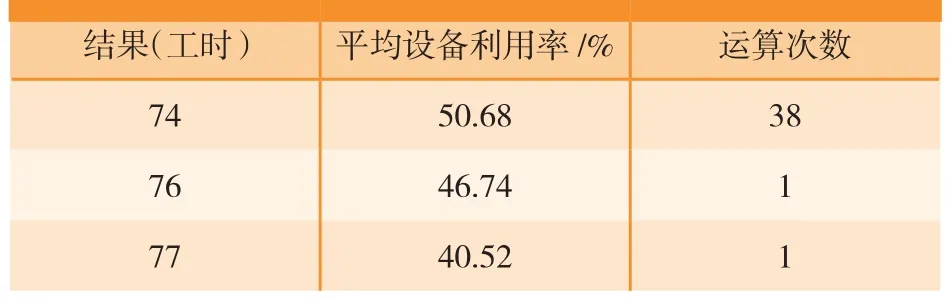
表4 试验运算结果

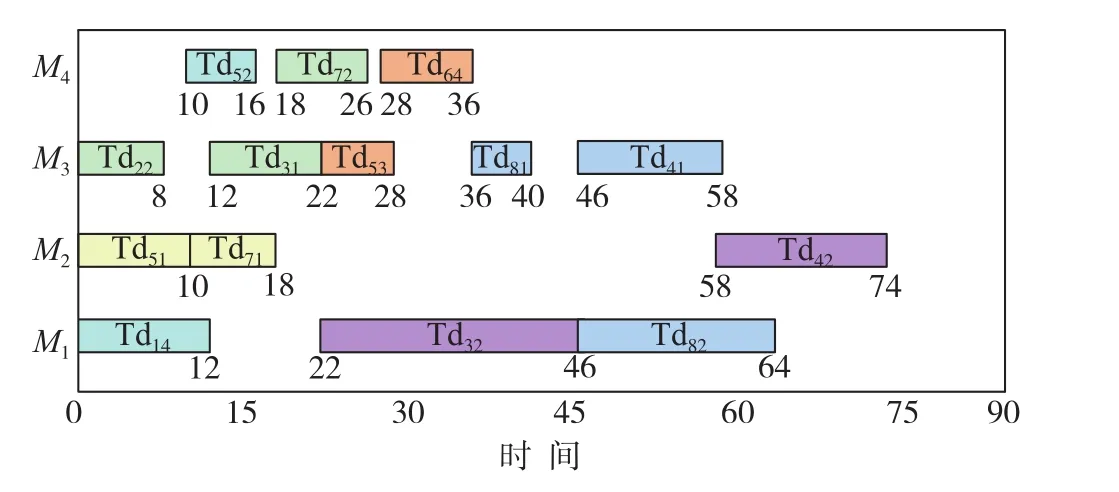
图6 设备调度顺序图Fig.6 Diagram of equipment scheduling sequence

为避免随机等因素干扰，本次试验运算40次，结果如表4所示。从表4可得，其中1次获得工时76，1次获得工时77，38次获得工时74，平均利用率为50.68%，工作时间设备1、设备2、设备3、设备4分别为 54、34、40、22。最佳染色体为P={P1，P2.2，P3.1，P4.1，P5.1，P6.2，P7.1，P8.1}，Pi.k表示第i个装配的第k种方案。调度结果如图6所示，Td表示工序， 对甘特图分析可得，夹具设备是生产作业瓶颈。

4 结束语

针对飞机装配过程设备调度的复杂性，提出了将面向对象Petri网与赋时Petri网相结合构建设备调度模型的新方法，该方法能够有效地将装配元变迁与辅助设备关联，且有效解决了模型的“空间爆炸问题”。同时在TPN模型中嵌入混合算法，利用装配元变迁和装配元设备库所集为染色体编码，以多目优化为基础对设备调度进行求解。实例应用与分析表明算法可行，能够缩短装配时间。本文下一步将继续研究OTPN模型中装配发生意外变更时设备调度的相关问题。

参 考 文 献

[1] 孙星.基于Petri网和eM-Plant的飞机装配线建模与仿真研究[D].南京：南京航空航天大学,2011.

SUN Xing. Modeling and simulation of aircraft assembly line based on Petri net and eM-Plant[D]. Nanjing: Nanjing University of Aeronautics &Astronautics, 2011.

[2] XU K, WANG C, ZHANG W, et al. Object-oriented aircraft assembly model[C]//International Conferece on Computer, Networks and Communication Engineering, Beijing, 2013.

[3] 谢志强，辛宇，杨静. 基于设备空闲事件驱动的综合调度算法[J]. 机械工程学报, 2011, 47(11):139-147.

XIE Zhiqiang, XIN Yu, YANG Jing. Integrated scheduling algorithm based on event-driven by machines’ idle[J]. Journal of Mechanical Engineering, 2011, 47(11):139-147.

[4] 孔令革，鲁建厦，詹燕.基于排队网络的生产物流瓶颈转移研究[J]. 浙江工业大学学报，2011，39(6): 644-647.

KONG Lingge, LU Jiansha, ZHAN Yan. Study on bottleneck shifting of production logistics based on queueing networks[J]. Journal of Zhejiang University of Technology, 2011, 39(6):644-647.

[5] 王成恩，于宏，张闻雷，等. 面向对象的航空发动机装配模型[J]. 计算机集成制造系统，2010，16(5):942-948.

WANG Cheng’en, YU Hong, ZHANG Wenlei, et al. Object-oriented aero-engine assembly models[J]. Computer Integrated Manufacturing Systems, 2010, 16(5): 942-948.

[6] 张杰，李原，张开富，等. 基于关系对象Petri网的飞机装配系统模型快速构建方法[J]. 计算机集成制造系统，2010，16(6): 1195-1201.

ZHANG Jie, LI Yuan, ZHANG Kaifu, et al. Rapid modeling method for aircraft assembly system based on relation-based object Petri nets[J].Computer Integrated Manufacturing Systems, 2010, 16(6):1195-1201.

[7] 徐开元，曲蓉霞，王健熙. 基于多域集成Petri网的飞机装配系统模型[J]. 计算机集成制造系统，2015，21(8): 2022-2032.

XU Kaiyuan, QU Rongxia, WANG Jianxi. An aircraft assembly system model based on multi domain integrated Petri net[J]. Computer Integrated Manufacturing System, 2015, 21(8): 2022-2032.

[8] 顾妍午，王遵彤，吴启迪. 面向对象Petri网技术在系统建模中的应用[J]. 同济大学学报（自然科学版），2010，38(3): 437-441.

GU Yanwu, WANG Zuntong, WU Qidi. Application of object oriented Petri net technology in system modeling[J]. Journal of Tongji University(Natural Science Edition), 2010, 38(3): 437-441.

[9] 刘维来，孔凡让，刘志刚，等. 基于遗传算法和延时Petri网的柔性装配系统的设备调度方法[J]. 计算机集成制造系统, 2006,12(8): 1246-1251.

LIU Weilai, KONG Fanrang, LIU Zhigang, et al. Facilities assignments of flexible assembly system based on GA and TPN[J]. Computer Integrated Manufacturing Systems, 2006, 12(8): 1246-1251.

[10] 彭勇刚，罗小平，韦巍. 一种新的模糊自适应模拟退火遗传算法[J]. 控制与决策, 2009, 24(6): 843-848.

PENG Yonggang, LUO Xiaoping, WEI Wei. A new fuzzy adaptive simulated annealing genetic algorithm[J]. Control & Decision, 2009, 24(6):843-848.

[11] 杨萌, ALMAINI A E A. 基于整体退火遗传算法的最佳混合极性搜索[J]. 复旦学报（自然科学版）, 2013, 52(3):303-308.

YANG Meng, ALMAINI A E A. Optimization of mixed polarity reedmuller functions based on whole annealing genetic algorithm[J]. Journal of Fudan University (Natural Science), 2013, 52(3): 303-308.