拓扑优化与增材制造结合：一种设计与制造一体化方法*

（大连理工大学工业装备结构分析国家重点实验室，大连 116024）

增材制造技术（Additive Manufacturing，AM）通过材料层层累加的方式实现结构的制备。这种独特的制造方式可实现高度复杂结构的自由“生长”成形，极大地拓宽了设计“空间”，为新型结构及材料的制备提供了强大的工具。然而，现有的增材制造结构，绝大部分仍然采用面向传统制造工艺的设计构型。这样所制备的结构并未充分利用增材制造所提供的新型设计空间，性能无法在本质上得到飞跃。甚至受限于增材制造技术的不成熟，其性能劣于传统制造工艺所制备的结构。因此，开展面向增材制造的设计方法研究，发展完整的设计理论体系，突破传统设计极限，获得优质创新结构构型已成为重要的研究方向。

随着科学技术尤其是计算机技术的快速发展，结构优化设计已成为结构创新设计的重要工具，一般可分为3类：尺寸优化、形状优化以及拓扑优化。其中，拓扑优化因其不依赖初始构型及工程师经验，可获得完全意想不到的创新构型，受到学者以及工程人员的广泛关注。通俗地讲，拓扑优化就是利用优化的手段，寻找结构内部哪里需要布置材料，布置何种材料，在保证一定约束下获取最优的性能（图1）。在航空航天、汽车能源等领域上，许多学者基于拓扑优化方法获得了前所未有的创新构型[1]，使得产品的结构性能或轻量化得到显著提升。

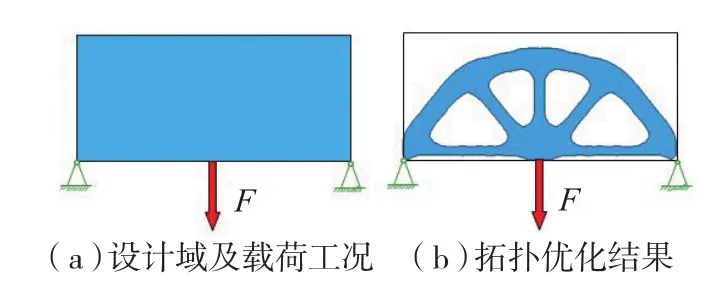
图1 拓扑优化示意图Fig.1 Illustration of topology optimization

然而，拓扑优化结果几何构型复杂，采用传统制造工艺制备非常困难，因此拓扑优化方法与实际工程结构设计之间仍存在较大的鸿沟。设计人员往往要基于制造技术及经验对优化结果进行二次设计，来满足可制造性，降低制造成本。这种做法往往会损坏结构的最优性，得到的结构性能甚至达不到已有构型。另一方面，受制于传统设计理念及制造工艺，结构往往仅进行宏观拓扑设计，并未充分利用结构在多尺度上的变化或者空间梯度变化所带来的广阔设计空间，使得产品性能提升非常有限。

增材制造技术的出现，使得几何形式高度复杂，且使从微纳到宏观多个几何尺度结构的制备成为可能。它颠覆了传统制造技术的局限，解决了产品研发存在的“制造决定设计”问题。因此，将拓扑优化（先进设计技术）与增材制造（先进制造技术）融合，发展创新设计技术具有广阔的前景，已引起学术界的广泛关注。航空结构创新研发具有小批量、多品种、高性能等特点。突破现有设计极限对结构创新设计技术及快速试制技术提出了更高的要求。增材制造作为一种“无模敏捷制造”技术，可大幅降低研发周期和成本，是“快速试制”的核心技术。西北工业大学黄卫东团队、北京航空航天大学王华明团队、西安交通大学卢秉恒团队等在金属增材制造上取得突破性成果，实现了部分大型复杂航空结构件的制备。拓扑优化作为先进的设计理论，可为航空结构创新设计提供强大的动力，大连理工大学程耿东院士和刘书田教授团队、西北工业大学张卫红教授团队等已成功将其应用在航空结构关键零部件设计中。研究面向增材制造的航空结构设计需要解决两个方面的问题：（1）如何充分利用增材制造技术所提供的设计空间，发展拓扑优化方法设计优质结构构型；（2）在拓扑优化时考虑增材制造技术其独特的制造约束，保证设计结果的可制造性。本文将针对以上两个关键问题开展详细的论述，介绍现有研究成果，并阐述未来的研究趋势。

面向增材制造的优质结构构型设计

整体结构层级化、材料属性梯度化、功能结构一体化、结构多功能化已成为新结构与材料的重要发展方向。基于增材制造工艺，突破传统设计“极限”，研发整体化、轻量化、低成本的高性能新结构和材料是新一代重大/高端装备与结构研制的迫切需求。本节将主要介绍基于拓扑优化方法，从4个方面设计创新优质结构构型。

1 特定/特异性能材料微结构拓扑优化设计

复合材料因具有传统单一材料所无法达到的性能，且具有良好的可设计性，受到研究人员的广泛关注。通过设计微结构的构型，获得具有特定/特异性能的周期性复合材料已成为材料领域的研究热点（图2），这种方式获得的新型材料也常称为构造化材料。拓扑优化技术为微结构构型设计提供了强大的工具，已开展了相当广泛的研究。该部分工作最早可追溯到Sigmund等[2]基于逆均匀化方法，设计了具有特定刚度（包括体模量、剪切模量及泊松比等）的微结构构型。此外，一些学者在其他性能（例如粘弹性性能、热性能、渗流等）的微结构设计上开展了大量工作。通过拓扑优化方法设计材料的微结构构型，可获得填补材料空白的高性能材料构型。然而受制于传统制造工艺的束缚，仅有少数高性能材料得到了制备。因此基于增材制造技术，实现高性能构造化材料的制备，已然成为研究的前沿问题。最近，Wang等[3]建立了考虑几何及材料非线性的特定应力-应变曲线微结构构型设计方法，并通过增材制造技术实现了所设计微结构的制备（图3），试验结果表明设计结果达到了所需性能[4]。

2 多层级结构拓扑优化设计

多层级结构设计是指在结构的宏观和微观等多个层级上同时设计结构的构型，如图4所示，这样可有效扩大设计空间，有利于获得性能优异的结构构型。例如2011年发表于Science，号称当时世界上最轻的材料就是微纳米多层级点阵材料（图5）[5]。

Rodrigues等[6-7]首次建立了多层级结构拓扑优化设计方法，如图6所示，给出了基于该方法得到的骨骼重构模型。为减少计算量并方便制备，大连理工大学程耿东等[8-10]提出了具有单一微结构构型的材料/结构一体化协同设计方法，实现了宏微观结构协同优化设计。

图2 基于拓扑优化设计微结构构型示意图Fig.2 Schematic illustration of the periodic microstructure based on topology optimization design

多层级结构的拓扑优化设计在沉寂了10年后，由于增材制造的快速发展，再次进入了一个新的研究热潮。然而，现有方法依然面临着许多技术难点，比如设计变量多、计算量过大等，如何在设计空间与计算效率上进行权衡，建立适用于工程结构设计的方法依然是未解决的难题。此外，现有设计大多基于均匀化方法将微结构等效为均质材料，未考虑结构的尺寸效应。为解决此问题，刘书田等[11]基于高阶偶应力设计材料微结构构型，阎军等[12]则将扩展多尺度有限元法应用到多层级结构设计上。

3 多材料结构拓扑优化设计

通过材料的合理布局，实现材料性质按需分配，可以大大提高结构性能，如图7所示。Sigmund等[13]首先基于变密度法提出了一种三相材料插值模型，Gaynor等[14]基于此设计并制备了一种柔性机构，如图8所示。

多材料拓扑优化方法经过20年的发展已经逐渐趋于成熟，但是考虑界面缺陷以及梯度层影响的研究还很缺乏[15]，有待进一步深入研究。另外，由于工艺限制，现有的多材料拓扑优化主要是面向分区均质多材料构型设计，近年来出现的增材制造技术可以通过改变不同材料在不同位置的组分比例实现空间内材料属性的变化。因此，增材制造技术为任意梯度变化多材料构型的制备提供了可能，这极大地释放了科研者的设计空间。因此，如何最大限度利用增材制造所释放的设计空间，同时考虑多材料构型制备工艺约束，是今后多材料布局优化的重要研究方向。

4 多功能结构拓扑优化设计

图3 泊松比范围为-0.8～0.8的微结构构型Fig.3 Optimized architectures by topology and shape with Poisson ratio of -0.8-0.8

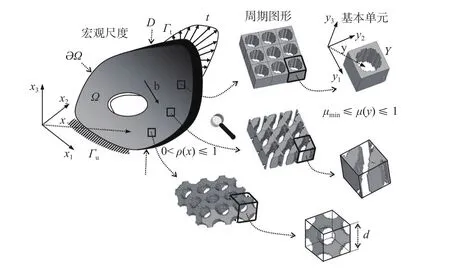
图4 多层级结构设计示意图Fig.4 Hierarchical optimization of material and structure

图5 超轻金属点阵材料Fig.5 Ultralight metallic microlattices

复杂部件级结构中除了承载功能外，往往还包括散热、减振、隐身及传导等其他功能。合理地设计结构构型，实现多功能化，是提升结构性能的有效方式。基于增材制造技术，可以制备内部含有复杂空腔、多种材料复合的新型结构，使得兼具承载和其他功能的部件有望实现。针对此，许多学者开展了多功能结构的拓扑优化设计方法研究，实现了比如减振降噪、承载-散热、传导及天线等结构设计。例如，刘书田等[16]基于拓扑优化设计了一种应用在探地雷达中的小型平面蝶形天线（图9），相对传统构型可有效降低工作频点。

基于拓扑优化的多功能结构设计虽然已得到蓬勃发展，但是由于多物理场问题分析求解困难，现有设计大多集中在只考虑2～3个独立的物理场。考虑多物理场耦合、多目标的拓扑优化设计方法仍处在研究初期，为实现设计结果的工程应用，此方向必将成为下一步研究的重点。

考虑增材制造工艺约束的拓扑优化设计方法

图6 基于多层级结构设计的骨骼重构Fig.6 Two-scale bone remodelling model

图7 多材料结构示意图Fig.7 Illustration of multi-material structure

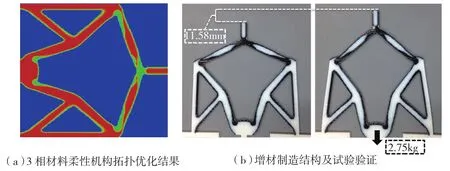
图8 柔性机构实例Fig.8 A sample of compliant mechanism

图9 探地雷达天线设计Fig.9 Topology optimization design of small GPR antennas

增材制造技术相对于传统制造工艺，因其独特的制造方式，可实现复杂几何结构构型的制备。然而，增材制造并非完全“自由”制造，仍然存在独特的制造约束，主要包括以下几类：结构最大/最小尺寸、支撑结构、制造缺陷（表面粗糙度、材料各向异性等）及连通性约束等。如何在拓扑优化设计过程中考虑增材制造工艺约束，实现拓扑优化结果的快速直接制备已经成为国内外学者关注的重点。

1 尺寸特征

不同3D打印设备具有不同的打印精度，因此需要控制拓扑优化结果的特征尺寸，避免无法制造的细杆等结构出现。图10分别给出了不考虑最小尺寸特征控制及考虑最小尺寸特征控制的拓扑优化结果。可以看出，对于图10（a）中存在的细微结构，对于一些打印机精度不是很高的机器，很难制备[17-18]。由于尺寸特征约束同样存在于传统制造工艺中，因此该方向很早就得到学者的广泛关注，已建立了比较完善的拓扑优化结果尺寸控制方法体系。

图10 拓扑优化结果尺寸特征控制Fig.10 Feature control in structural topology optimization

2 自支撑结构设计

增材制造过程中，对于大悬挑结构，往往需要在其下方添加支撑结构，以防止制造工程中结构坍塌，如图11所示。支撑结构的使用，不仅仅会带来打印时间及成本的增加，而且在后期去除时，带来工艺难度，影响结构最终表面精度。因此设计自支撑结构，在优化过程中自动识别特征结构，避免大悬挑结构，成为研究的热点。

部分学者在此方向做了初步探索，然而现有的模型大多基于理论假设，结构坍塌极限与材料属性、悬挑角度以及悬挑长度等关系，并未通过大量的试验精确获得[19]。因此，建立Benchmark模型，开展大批量试验研究，提出精确地自支撑标准，以此为基础开展拓扑优化设计方法是未来的研究趋势。

3 制造缺陷

图11 大悬挑结构及支撑结构示意图Fig.11 Illustration of cantilevered structure and supporting structures

图12 封闭结构内部无法去除支撑结构Fig.12 Structure with enclosed void

近几年，增材制造技术虽得到了飞速的发展，然而整体来看该制造工艺仍处于技术萌芽初期，尚未成熟。受工艺限制，增材制造结构件往往存在一些缺陷，例如材料各向异性、表面粗糙以及材料属性不确定等。针对该问题，一些学者将制造缺陷考虑到拓扑优化模型中，以减小缺陷对结构性能的影响[20-21]。然而，在实际计算过程中，所使用的缺陷模型大多为理论模型，与增材制造工艺引起的不确定模型并不相符。因此，基于试验研究增材制造的材料成形机理，建立真实缺陷模型，并引入到拓扑优化过程中，是未来研究的目标。

4 连通性约束

增材制造过程中，无论是采用熔融沉积成型（FDM）或者激光选择性烧结粉末技术（SLS），都需要在结构打印结束后去除支撑材料或者未熔融的金属粉末，因而要求结构内部不能含有封闭的内部孔洞。对于含内部孔洞的结构，由于无法去除支撑材料或者未熔融的金属粉末，常常需要二次修正或者结构分区制造（图12），大大增加了制造的工艺难度，提高了成本。Liu等[22-23]提出了一种基于虚拟温度比拟的结构连通性描述方法，将连通性约束转化为结构的最大温度小于一有限值这一简单且有效的新约束，成功地应用于结构拓扑优化设计中，实现了最优拓扑结构的连通性控制（图13），并应用到背部封闭大口径反射镜设计中[24]。

图13 考虑不同连通性约束设计结构Fig.13 Real objects of the optimized structures without and with manufacturing process constraints

结论

伴随着增材制造工艺的快速发展，建立面向增材制造的创新设计理论和方法，获得具有可制造性（可制造性设计）的优质构型（优质构型设计），已成为当今设计师和研究人员所面临的新课题。拓扑优化技术经过几十年的发展，已在优质构型设计上（构造化材料、多层级结构、多材料结构及多功能结构）开展了丰富的研究，可充分利用增材制造技术释放极大的创新设计空间。如何将拓扑优化（先进的设计工具）与增材制造技术（先进的制备工具）相结合，实现结构创新能力的飞速提升，必将成为未来10年研究的重点和热点。

参 考 文 献

[1] LIU S T, HU R, LI Q H, et al. Topology optimization-based lightweight primary mirror design of a large-aperture space telescope[J].Applied Optics, 2014,53(35):8318-8325.

[2] SIGMUND O. Materials with prescribed constitutive parameters: an inverse homogenization problem[J]. International Journal of Solids and Structures, 1994,31(17):2313-2329.

[3] WANG F, SIGMUND O, JENSEN J S. Design of materials with prescribed nonlinear properties[J]. Journal of the Mechanics and Physics of Solids, 2014,69:156-174.

[4] CLAUSEN A, WANG F, JENSEN J S, et al. Topology optimized architectures with programmable Poisson's ratio over large deformations[J]. Advanced Materials,2015,27(37):5523-5527.

[5] SCHAEDLER T A, JACOBSEN A J, TORRENTS A, et al. Ultralight metallic microlattices[J]. Science, 2011,334(6058):962-965.

[6] RODRIGUES H, GUEDES J M,BENDSOE M P. Hierarchical optimization of material and structure[J]. Structural and Multidisciplinary Optimization, 2002,24(1):1-10.

[7]COELHO P G, FERNANDES P R,GUEDES J M, et al. A hierarchical model for concurrent material and topology optimization of three-dimensional structures[J]. Structural and Multidisciplinary Optimization, 2007,35(2):107-115.

[8]CHEN W J, TONG L Y, LIU S T. Concurrent topology design of structure and material using a two-scale topology optimization[J]. Computers & Structures,2017,178:119-128.

[9]LIU L, YAN J, CHENG G D. Optimum structure with homogeneous optimum trusslike material[J]. Computers & Structures,2008,86(13):1417-1425.

[10]YAN J,CHENGG D, LIU L.A uniform optimum material based model for concurrent optimization of thermoelastic structures and materials[J]. International Journal for Simulation and Multidisciplinary Design Optimization, 2008,2(4):259-266.

[11]SU W Z, LIU S T. Topology design for maximization of fundamental frequency of couple-stress continuum[J]. Structural and Multidisciplinary Optimization, 2016,53(3):395-408.

[12]YAN J, HU W B, WANG Z H, et al. Size effect of lattice material and minimum weight design[J]. Acta Mechanica Sinica,2014,30(2):191-197.

[13]SIGMUND O, TORQUATO S. Design of materials with extreme thermal expansion using a three-phase topology optimization method[J]. Proceedings of SPIE, Smart Structures and Materials,1997,45(6):1037-1067.

[14]GAYNOR A T, MEISEL N A,WILLIAMS C B, et al. Multiple-material topology optimization of compliant mechanisms created via PolyJet three-dimensional printing[J]. Journal of Manufacturing Science and Engineering,2014,136(6):1-10.

[15]LIU P, LUO Y J, KANG Z. Multimaterial topology optimization considering interface behavior via XFEM and level set method[J]. Computer Methods in Applied Mechanics & Engineering, 2016,308:113-133.

[16]LIU S T, WANG Q, GAO R J. A topology optimization method for design of small GPR antennas[J]. Structural and Multidisciplinary Optimization, 2014,50(6):1165-1174.

[17]白伟, 李取浩, 陈文炯, 等. 基于映射的拓扑优化最大尺寸控制方法[J/OL]. 工程力学, 2017: [2017-02-07]. DOI:10.60521j.issn.1000-4750.2016.04.0309.

BAI Wei, LI Quhao, CHEN Wenjiong,et al. A novel projection based method for imposing maximum length scale in topology optimization[J/OL]. Engineering Mechanics,2017: [2017-02-07]. DOI:10.60521j.issn.1000-4750.2016.04.0309.

[18] WANG F, LAZAROV B S, SIGMUND O. On projection methods, convergence and robust formulations in topology optimization[J].Structural and Multidisciplinary Optimization,2001,43(6):767-784.

[19]BRACKETT D, ASHCROFT I,HAGUE R. Topology optimization for additive manufacturing[C]//Proceedings of the 24th Solid Freeform Fabrication Symposium. Austin:University of Texas at Austin, 2011.

[20]SIGMUND O. Manufacturing tolerant topology optimization[J]. Acta Mechanica Sinica,2009,25(2):227-239.

[21]SCHEVENELS M, LAZAROV B S, SIGMUND O. Robust topology optimization accounting for spatially varying manufacturing errors[J]. Computer Methods in Applied Mechanics and Engineering, 2011,200(49-52):3613-3627.

[22]LIU S T, LI Q H, CHEN W J, et al. An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures[J]. Frontiers of Mechanical Engineering, 2015,10(2):126-137.

[23]LI Q H, CHEN W J, LIU S T, et al.Structural topology optimization considering connectivity constraint[J]. Structural and Multidisciplinary Optimization, 2016,54(4):971-984.

[24]HU R, CHEN W J, LI Q H, et al. Design optimization method for additive manufacturing of the primary mirror of a largeaperture space telescope[J]. Journal of Aerospace Engineering, 2017,30(3):1-10.