微球内部电磁场的Mie理论数值计算

沈建琪, 邱俊程

(上海理工大学 理学院,上海 200093)

微球内部电磁场的Mie理论数值计算

沈建琪, 邱俊程

(上海理工大学 理学院,上海 200093)

采用Mie散射理论对平行光束与微球颗粒相互作用的内部场进行严格的描述并进行数值计算.对吸收性微球颗粒内部场进行数值计算时,如果粒径及折射率虚部较大,其径向函数会出现数据溢出,从而导致计算失败,得出不合理的计算结果.通过引进径向函数的变形,提出了一种克服数据溢出的算法,将径向函数的数值控制在合适的范围以内.通过数值计算得到了合理的结果,证明该算法克服了数据溢出,可以稳定地计算各种平行光照射下的微球颗粒内部场.

Mie理论; 内部场; 数值计算

球形颗粒与平面电磁波(平行光)的相互作用可以通过Maxwell方程组得到严格解,即Lorenz Mie理论[1-2].随着微光学技术的不断发展,人们对微球内部电磁场及其分布的研究越来越重视.微球内部电磁场分布在微激光的研制、医学应用等领域具有重要价值[3-5].对微球内部电磁场的数值计算是研究微球内部电磁场分布及其谐振机制、热效应等特性的基础,涉及到球坐标系中的特殊函数计算,包括对Bessel函数和缔合勒让德函数的计算.非耗散性微球的折射率为实数,内部电磁场的数值计算相对容易.但耗散性微球的折射率为复数,对应的数值计算比较困难,需要克服数据溢出的问题.现有文献主要针对粒径较小和非耗散性(或弱耗散)微球内部场的研究,对于粒径较大的情况主要通过几何光学近似计算[6-9].

本文对微球内部电磁场的数值计算方法进行研究,重点考虑耗散性微球折射率参数对特殊函数计算的影响,提出了一种克服数据溢出的算法,并通过数值计算进行验证.

1 内部场表达式

如图1所示,根据Mie散射理论,时谐项取exp (-iωt),且入射光是电矢量沿x方向振动、沿z轴方向传播的线偏振光时,微球内部电磁场场强在球坐标系中的3个分量[2]分别为

(1)

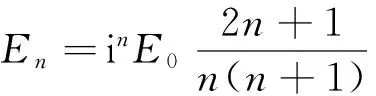
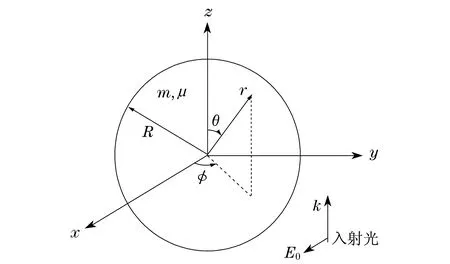
图1 偏振平行光与微球相互作用示意图

(2)

它们满足如下递推关系:

(3)

其初始值为π0=0,π1=1.

Mie系数cn和dn的表达式为

(4)

第一类Riccati-Bessel函数和第一类Riccati-Hankel函数以及它们的导数满足相同的递推关系.

(5)

(6)

2 算法描述

根据式(1),微球内部电磁场是无穷多个分波的叠加,其高阶项较弱,因此,在数值计算中可选取一个截止项,对应的截止阶数ns由下式决定[10-11]:

(7)

微球内部电磁场的计算包含了散射角函数πn和τn的计算、Mie系数cn和dn的计算以及径向函数ψn(ρ)和ψ′n(ρ)的计算.散射角函数πn和τn的数值计算可由式(3)给出的递推关系从低阶函数π0和π1依次迭代得到,其数值在计算机可执行范围内不存在溢出问题.

Mie系数cn和dn的计算和径向函数ψn(ρ)和ψ′n(ρ)的计算需要考虑复数折射率导致的溢出问题.与时谐项exp(-iωt)相对应,折射率的虚部为正数,m=mre+imim(即mim≥0).因此,无因次径向参数ρ=mkr也是一个复数,且靠近微球边界(即r→α)时,ρ的虚部会比较大,ρim→mimα.从式(6)给出的递推公式及其初始值可知,ψn(ρ)和ψ′n(ρ)与exp(ρim)成正比.因此,如果mimα很大,ψn(ρ)和ψ′n(ρ)可能溢出,导致计算失败.基于同样的原因,Mie系数cn和dn的数值计算存在同样的问题.因此,在计算内部场分布时,为了克服数值的溢出,需要进行相关的处理.将式(1)的内部场表达式改写为

(8)

对Mie系数cn和dn的表达式(式(4))作进一步推导,可得

(9)

(10)

(11)

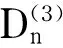
(12)

式(10)中函数Nn(α,β)的计算可采用如下递推关系:

(14)

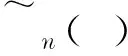
(15)

3 数值计算验证

微球内任意一点的电场能量密度

(16)

式中,ε1是微球的介电常数.

当入射光为自然光时,内部电场各分量为

(17)

本文仅考虑微球内部场的分布,不考虑场的绝对大小.为简便起见,在以下的数值计算中取ε1/4=1.

图2给出了采用式(8)计算得到的粒径无因次参数α=200时,各种不同折射率的微球内部场曲面分布图.其中,水滴的折射率为m=1.33,Cu,Ag和Al微球在入射光波长为632.8 nm时的复数折射率分别为m=0.307 03+3.434 5 i,m=0.156 67+3.804 5 i和m=1.266 7+7.281 1 i.

图2 各种不同折射率的微球内部场曲面分布图

数值计算显示,当微球折射率为实数或折射率虚部较小(图2(a)和2(b))时,式(1)和式(8)的数值计算结果相同.但是,当微粒折射率虚部较大(图2(c)和2(d))时,采用式(1)计算内部场遇到数据溢出问题;而采用式(17)计算依然可以得到合理的结果.这是由径向参数ρ=mkr虚部(即ρim)的大小决定的.在式(1)的计算中,其中间变量与e-ρim有关,当ρim≥710时,可导致数值出现溢出.在所考虑的几个算例中,水滴的ρim=0,因此,式(1)和式(8)实际上是一致的,可以得到完全一致的计算结果.对于Cu,Ag和Al微球,径向参数虚部的值分别为ρim=686.9,ρim=760.9和ρim=145 6.因此,Cu微球的两种计算方法结果一致,而Ag和Al微球的计算只能采用式(17).

从各种不同的吸收情况(对应不同的复数折射率)来看,非吸收性微球内部场遍及了整个微球,且在前向和后向具有较强的分布.对于吸收性微球,由于媒质的吸收效应,内部场主要分布在微球表面部分.

图3给出了采用式(17)计算得到的粒径无因次参数α=200时,不同波长的入射波照射下Li微球内部场曲面分布图.

数据计算结果显示,随着入射波波长的增大,Li微球对光能量的吸收增强,与之相对应,在颗粒吸收能力较弱时内部场比较强.反之,随着吸收的增强,内部场逐渐减小,并趋向于在微球表面集中.

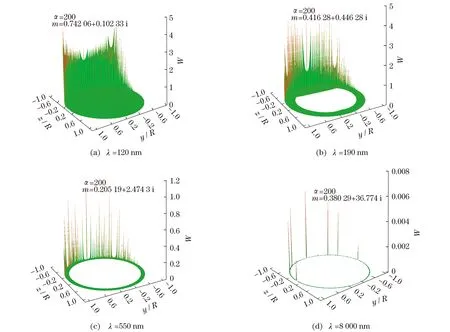
图3 不同波长入射波照射下Li微球内部场曲面分布图

4 结 论

在Mie理论内部场数值计算中,其径向函数(即Riccati-Bessel函数和Riccati-Hankel函数)的数值范围与微球颗粒的吸收特征(即复数折射率的虚部)有关,强吸收情况下会导致数据溢出.本文对径向函数进行变形处理,将数值控制在合理的范围内,克服了数据计算溢出问题.不同吸收参数情况下的数值计算结果表明,该算法稳定可靠,可以得到合理的计算结果.

[1] VAN DE HULST H C.Light scattering by small particles[M].New York:Dover Publications,1981.

[2] BOHREN C F,HUFFMAN D R.Absorption and scattering of light by small particles[M].New York:John Wiley & Sons,1983.

[3] DATSYUK V V.Optics of microdroplets[J].Journal of Molecular Liquids,2001,93(1/2/3):159-175.

[4] LIN H B,CAMPILLO A J.Microcavity enhanced Raman gain[J].Optics Communications,1997,133(1/2/3/4/5/6):287-292.

[5] ARNOLD S,HOLLER S,GODDARD N L.Fluorescence microscopy and spectroscopy of an isolated micro-droplet[J].Materials Science and Engineering:B,1997,48(1/2):139-146.

[6] KAI L,D’ALESSIO A.Internal-field characteristics of spherical particles[J].Particle & Particle Systems Characterization,1995,12(5):237-241.

[7] LAI H M,LEUNG P T,POON K L,et al.Characterization of the internal energy density in Mie scattering[J].Journal of the Optical Society of America A,1991,8(10):1553-1558.[8] VELESCO N,KAISER T,SCHWEIGER G.Computation of the internal field of a large spherical particle by use of the geometrical-optics approximation[J].Applied Optics,1997,36(33):8724-8728.

[9] LI C H,KATTAWAR G W,ZHAI PW,et al.Electric and magnetic energy density distributions inside and outside dielectric particles illuminated by a plane electromagnetic wave[J].Optics Express,2005,13(12):4554-4559.

[10] BOTT A,ZDUNKOWSKI W.Electromagnetic energy within dielectric spheres[J].Journal of the Optical Society of America A,1987,4(8):1361-1365.

[11] WISCOMBE W J.Improved Mie scattering algorithms[J].Applied Optics,1980,19(9):1505-1509.

[12] SHEN J Q.Algorithm of numerical calculation on Lorentz Mie theory[J].PIERS Online,2005,1(6):691-694.

[13] LENTZ W J.Generating Bessel functions in Mie scattering calculations using continued fractions[J].Applied Optics,1976,15(3):668-671.

[14] SHEN J Q,WANG H R.Calculation of Debye series expansion of light scattering[J].Applied Optics,2010,49(13):2422-2428.

(编辑:石 瑛)

Numerical Calculation of the Electromagnetic Field Inside the Microsphere with Mie Theory

SHEN Jianqi, QIU Juncheng

(CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The classical Mie theory was used to exactly describe the field inside the sphere in the interaction between the parallel beams and microsphere particles.If the particle size and the imaginary part of the refractive index are large,The data overflow by the calculation of radial function for an absorbing microsphere particle will appear,which leads to the failure of the calculation,and the unreasonable results are obtained.In order to overcome the overflow,an algorithm was proposed by introducing modified radial functions so as to keep their values in an appropriate range.Numerical calculations were conducted and reasonable results were obtained.The results demonstrate that the algorithm can overcome the data overflow successfully,and it can also be used to calculate any internal field of microsphere particles interacting with various parallel optical beams.

Mietheory;internalfield;numericalcalculation

1007-6735(2017)02-0159-06

10.13255/j.cnki.jusst.2017.02.011

2016-05-19

国家自然科学基金资助项目(NSFC51476104)

沈建琪(1965-),男,教授.研究方向:光散射理论与颗粒测试技术研究.E-mail:jqshenk@163.com

O 436

A