关于磁单极子问题研究的一种新的尝试
倪卫新, 孙 凯
(上海理工大学 理学院,上海 200093)
关于磁单极子问题研究的一种新的尝试
倪卫新, 孙 凯
(上海理工大学 理学院,上海 200093)
磁场的高斯定律从形式上指出了宏观磁场的无源性质,因此可以利用高斯积分是否为零作为判断磁单极子是否存在的形式判据.根据高等量子力学的理论,借助贝瑞相的存在,从形式上找到微观系统磁单极子存在的依据.并且由于贝瑞相和光霍尔效应存在相关性,通过求解光霍尔效应的久期方程,从形式上探讨了在微观条件下磁单极子存在的可能性和条件.
磁单极子; 高斯定理; 贝瑞相; 光霍尔效应
磁单极子即磁单极,是指单独具有一个N极或S极的磁性物质[1].磁单极子是一种到目前为止还基本上只存在于理论之中的物质,磁单极子作为物质的基本组成,它的单独存在可能非常困难,或者可能极其微弱以致无法测量.1931 年,英国物理学家狄拉克在提出“反电子”理论之后,首先提出了磁单极子的存在[1].自20世纪30年代以来,探究磁单极子的存在一直是困扰物理学家和天文学家的热门话题.尽管对于磁单极子问题的探究仍没有获得突破性的进展,但物理大统一理论以及对早期宇宙的研究,都认为磁单极子是存在的.通过实验来探测磁单极子,已经成为检验粒子物理大统一理论和天体物理宇宙演化理论的重要依据.长期以来,物理学家一直试图通过实验来证实自然界中磁单极子的存在[1-2].本文试图通过“电”和“磁”的高斯理论的比较,从形式上给出磁单极子是否存在的判据,并且通过贝瑞相与光霍尔效应之间的关联,给出对微观场合磁单极子存在的可能性的判断和猜想.
1 狄拉克假定
1931年,为解释电荷的量子化现象,狄拉克首次从理论上预言磁单极子的存在,他认为这些带有磁场的粒子能够存在于一些狄拉克弦(Dirac string)的末端.电荷e和磁核g满足关系式

当N=1时,得到的基本磁核的量值g0远大于e,这是磁单极子的一个重要特性,这表明异性磁荷之间具有远大于异性电荷之间的吸引力,因此要获得游离的单个磁单极子就需要用很大的外力才能将成对的磁偶极子分开.狄拉克认为这样就可以解释为什么电子容易发现而磁单极子却难以找到.此外,根据式中N为整数,还可以推测出磁荷和电荷的不连续性,进而解释物理学中电荷量子化的难题.
从上面的公式可以看出,假如磁单极子存在,电子和磁单极子的关系是显著存在的,磁单极子之间具有很强的吸引力,很难以游离的形式存在,且质量很小,很难被发现.在现有的物理学体系中,点电荷是明确知道其存在的,现今研究的磁单极子与点电荷具有很多相同的性能,可以将磁单极子具象成一个点磁荷来进行探究.如果类比的这个磁荷在现有可探究的实验现象中能够找到和点电荷相同的性质,那么就可以大胆地推测磁单极子的存在.电荷和磁荷周围都存在着某种看不见、摸不着而且稳定存在的物质,即电场和磁场,通过类比点电荷与点磁荷之间电场和磁场的差异,可以对磁单极子的存在进行探究.
2 高斯定理
18世纪中期,麦克斯韦在总结早期电磁理论的基础上,提出了关于电磁理论著名的麦克斯韦方程组,从此人类对电磁领域的研究达到了新的高度.麦克斯韦方程组的前两个方程正是分别关于电通量ΦE和磁通量ΦB的高斯定理[3-4].
(1)
方程(1)指出,在静电场中,通过任意一个闭合曲面S的电通量ΦE等于该面所包围的所有电量qi的代数和除以ε0,与闭合面外的电荷无关.
通过对点电荷电场中高斯定理的探究,可以得到以下几个结论:

b. 通过不包围点电荷的任意闭合曲面S的电通量恒为0;
c. 多个点电荷的电通量等于它们单独存在时的电通量的代数和.
而这种结论在磁场中并不成立,方程(2)正是这种结论的表达.
(2)
式中,B表示磁感应强度.
由于载流导线产生的磁感应线是无始无终的闭合线,可以想象,在磁场中,通过任意闭合曲面S的磁通量都等于0,通过类比点电荷在电场中的表现,可以得出以下两种可能存在的结果:
a. 假设的点磁荷理论并不成立,单个的磁单极子并不存在;
b. 磁单极子存在,但是其体积极小,磁偶极子联系紧密,只能在微观层面观察,在宏观世界中无法探究其存在.
在经典电磁理论中,磁感应强度的高斯定理明确地表明:类似于静电场源的静电荷,在磁场中无法找到相对应的磁荷,由此决定了电场和磁场的不同特征.也可以证明,在经典电磁学中,并不能够证明磁单极子的存在.
3 Berry几何相与磁单极子问题
根据文献[5],倪光炯等编著的高等量子力学是这样讨论贝瑞相的:考虑一个量子体系的哈密顿(Hamilton)量,用符号H来表示,H(R(t))依赖于含时参量R(t),且周期演化,周期为τ,R(τ)=R(0).

(3)
(4)
设H(R(t))的瞬时本征方程为


(6)

(7)
(8)
(9)


(10)
(11)
(12)


利用Stoke’s定理,γm(C)还可以化为参数空间中的面积分.

即
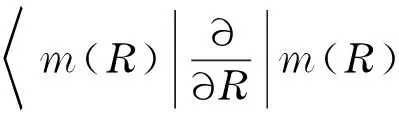
由式(11)可以推出γm(C)为实,类比式(13)与前文中关于点磁荷的假设,此时,可以推测出磁单极子存在的可能性.

利用×(ua)=u×a+u×a化为
再利用
得
(16)
定义厄米算符
(17)
则
式(16)可以表示成为
(19)
所以
利用


在上式中,找到了一个点可以使得磁通量积分不为0,与前文中提出的“点电荷与点磁荷”理论进行对比,可以发现,在微观上找到了磁单极子理论上存在的依据,这种发现也可以更好地解释反霍尔效应的现象.可以进一步大胆推测,这个使得磁通量积分不为0的点即为磁单极子存在的奇点.可证明,磁单极子奇点出现在能级简并处.当然贝瑞相的研究并不局限于磁单极子问题[6-7].
4 一个典型案例:光霍尔效应中的Berry相
根据电磁场理论,把电流通过导体所产生的横向电压效应称为霍尔效应.而当光线通过晶体时也会产生光的振动矢量和晶体折射率有关的横向偏振,俗称光霍尔效应[8-9].
通过对光霍尔效应的研究,人们发现了一个原本被忽视的现象:Berry相在解释光霍尔效应产生机制中的作用.
根据自旋为1/2的粒子在旋转磁场中的Berry相的计算方式[10-11],尝试计算光霍尔效应中的Berry相.以自旋为1的光子取代自旋为1/2 的电荷,以折射系数的变化取代电势的变化.此方法最早发布于文献[12].
可设通过晶体的光子的哈密顿量为
则
(20)
式中:Ky为波矢量;δ为光子的微小偏移量.
粒子演化满足薛定谔方程
(21)
在绝热近似条件下,设任意时刻系统的演化波函数为
(22)
式中,ω0为初态角频率.
把式(20)和式(22)代入粒子的薛定谔方程式(21)中,得
化简得
其久期方程式的行列式为
通过求解得
式中,Ω=δKy-ω0.
假定当偏移量δ=δ0(δ0为偏移量初始值)时,使得介质的折射率缓慢变化成为一个周期T的变化,则系统的总相位应为
此处引入-2π是为了使系统在初始位置时,总的相位为零.在绝热近似,即ω0≪ω时,上式可以化为
式中:ω为角频率,±ωT为动力学相;∓Ω(C)为对应不同自旋态时的Berry相,Ω(C)=2π(1-cosθ),为系统演化时所经闭合路径对原点所张的立体角.这个简单计算的结论告诉我们:光霍尔效应中贝瑞相不但存在,而且可以测量.
5 结 论
通过对磁单极子与Berry几何相关系的探究和Berry几何相与光霍尔效应的探究,从中发现了三者之间的关系,光霍尔效应的探究为Berry几何相的存在提供了实验依据.而在进一步的Berry几何相与磁单极子关系的探究中发现,在微观条件下,出现了一个可以使磁通量积分不为0的点,类比于前文得出的初步结论,有理由相信在能级简并处存在着磁单极子.但在光霍尔效应中如何具体定义出磁单极子还是一个未能解决的问题,至少形式上找到了磁单极子存在的依据.我们猜测:只要有贝瑞相存在的场合均有可能找到磁单极子.
[1] 李国栋.磁单极子理论和实验的发展[J].自然辩证法通讯,1983(2):29-37.
[2] 叶禹卿.磁单极子浅析[J].北京教育学院学报(自然科学版),2006,1(1):15-19.
[3] 郭硕鸿.电动力学[M].第3版.北京:高等教育出版社,2008.
[4] 程守洙,江永之.普通物理学:上册[M].6版.北京:高等教育出版社,2006.
[5] 倪光炯,陈苏卿.高等量子力学[M].2版.上海:复旦大学出版社,2004.
[6] SUN H Y,WANG L C,YI X X.Berry phase in a bipartite system with general subsystem-subsystem couplings[J].Physics Letters A,2007,370(2):119-122.
[7] WUNDERLICH J,KAESTNER B,SINOVA J,et al.Experimental observation of the spin-hall effect in a two-dimensional spin-orbit coupled semiconductor system[J].Physical Review Letters,2005,94(4):047204.
[8] XU C T,HE M M,CHEN G.Berry phase of coupled two arbitrary spins in a time-varying magnetic field[J].Chinese Physics,2006,15(5):912.
[9] HOSTEN O,KWIAT P.Observation of the spin hall effect of light via weak measurements[J].Science,2008,319(5864):787-790.
[10] 胡连,颜玉珍.高自旋粒子在旋转磁场中的演化及Berry相[J].华南理工大学学报(自然科学版),2004,32(7):74-77.
[11] 颜玉珍.自旋为1粒子在旋转磁场中的演化及几何相[J].嘉应学院学报(自然科学),2005,23(3):19-21.
[12] 倪卫新.光霍尔效应中的贝瑞相[J].科技创新导报,2015(29):239-240.
(编辑:丁红艺)
New Attempt to Study the Problem of Magnetic Monopole
NI Weixin, SUN Kai
(CollegeofSience,UniversityofShanghaiforScienceandTechonlogy,Shanghai200093,China)
The Gauss theorem points that the macro magnetic field is of no source in forms.In other words,it can be used as a criterion for judging the existence of magnetic monopole.But in the micro-world,the magnetic monopole can be found by means of testing the existence of the Berry-phase.A new style method was developed to discuss the possibility of the existence of magnetic monopole in micro area by comparing the Berry-phase and Hall effect of light.Based on the theories in macro and micro areas,a simple theoretical derivation was presented to probe into the possibility of the existence and conditions of “magnetic monopole”.
magneticmonopole;Gausstheorem;Berry-phase;Halleffectoflight
1007-6735(2017)02-0165-05
10.13255/j.cnki.jusst.2017.02.012
2016-07-26
倪卫新(1957-),男,讲师.研究方向:光学、理论物理.E-mail:nwxysp@qq.com
O 436
A

