混合分数跳-扩散模型下的亚式期权定价
耿延静,周圣武
(中国矿业大学数学系,江苏徐州221008)
混合分数跳-扩散模型下的亚式期权定价
耿延静,周圣武
(中国矿业大学数学系,江苏徐州221008)
给出了标的资产服从混合分数跳-扩散过程的几何平均亚式期权定价的解析解.运用广义Itˆo引理和自融资交易策略得到混合分数布朗运动下带跳的几何平均亚式期权定价的偏微分方程模型.结合边值条件,通过求解该偏微分方程得到亚式期权定价的解析解.通过数值试验,讨论各定价参数对期权价值的影响.本文推广了一些已有的结论,所得结果更贴近实际金融市场.
混合分数跳-扩散过程;几何平均亚式期权;偏微分方程
0 引言
亚式期权是一种强路径依赖型期权,在期权到期日的收益依赖于在整个期权有效期内标的资产所经历的价格平均值,因此亚式期权广受欢迎.Kemna和Vorst[1]通过波动率的变化求出了几何平均亚式期权定价的解析公式;Wong和Cheung[2]研究了随机波动率模型下的亚式期权定价模型;Ching-Sung Chou[3]推出了跳-扩散过程下的亚式期权定价模型.
经典的期权定价模型都假设金融资产价格(如股价)服从几何布朗运动,但大量的实证研究结果表明,金融资产价格并不服从几何布朗运动,而是呈现出一种“尖峰厚尾”的分布,且存在自相似性和长期相关性;分数布朗运动正好具备这些性质,能够更好地刻画金融资产价格的演化过程.但是分数布朗运动既不是Markov过程,又不是半鞅,所以不能使用通常的Itˆo积分来计算,这给分数布朗运动下的期权定价研究带来了一定的困难.于是Cheridito[4-5]建议使用混合分数布朗运动作为噪声来驱动一个金融资产的价格,这种噪声有着与半鞅类似的性质.Kuznetsov[6]、Z¨ahle[7]和Mishura[8]建立了混合分数布朗运动下的Black-Scholes定价模型.王晓天[9-10]研究了分数布朗运动下带交易费用的Black-Scholes模型的欧式期权定价以及分数布朗运动下带交易费用的有波动率微笑的欧式期权定价问题.大部分对奇异期权的研究都假设标的资产满足连续扩散过程,然而在实际金融市场中股票价格可能会出现“跳跃”,不少学者考虑用Poisson过程和布朗运动驱动的随机微分方程来描述股票价格变化并且给出了一些期权价格的解析解.Farshid Mehrdoust等[11]给出了算术平均亚式期权在带跳的双因素随机波动率模型下的数值解;Nisha Rambeerich[12]给出了当标的资产服从跳-扩散过程的欧式期权和美式期权的数值解.近年来,不少学者在对期权进行定价时将以上两种情况同时考虑进去.肖伟林[13]运用等价鞅测度方法求解出在分数跳-扩散过程下欧式货币期权的解析解;彭斌[14]利用分数跳-扩散过程的Itˆo公式给出了几何平均亚式期权定价公式并使用控制变量的方法对算术平均亚式期权进行蒙特卡罗模拟.丰月姣[15]和孙玉东[16]等利用分数跳-扩散过程的Itˆo公式研究了带跳的混合分数布朗运动下的利差期权定价问题.FoadShokrollahi[17]运用保险精算法得到混合分数跳-扩散过程下的利差期权定价公式.
本文假定股票价格遵循混合分数跳-扩散过程,利用混合分数跳-扩散过程随机分析理论,得到了混合分数-跳扩散环境下几何平均亚式期权价格所满足的Black-Scholes偏微分方程,并通过求解该偏微分方程,给出了几何平均亚式期权的定价公式.
1 定价模型
考虑一个股票价格既有连续又有间断的复杂的金融市场,对于连续部分有“尖峰厚尾”和“长期相关性”的特性,对于间断部分在价格过程中有异常波动.假设交易不需要支付交易费用,那么价格过程可由以上两个部分叠加组成,可写成如下形式
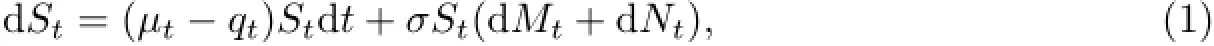
其中常数µt表示股票价格的预期收益率,常数qt表示股票支付的红利率,常数σ表示股票价格的波动率,是混合分数布朗运动,Bt是一个标准布朗运动,是赫斯特指数H∈(0,1)的分数布朗运动;Nt=Qt-λt是补偿泊松过程,Qt是强度为λ的泊松过程,且Qt、Bt、相互独立.
定理1(混合分数跳-扩散过程公式)假设Wt=Bt+均属于L2(P),
那么

因f(t,Wt)在t1时刻的变化量为f(t1,Wt1)-f,故

当跳跃次数i在区间(0,t)服从泊松过程时,则有
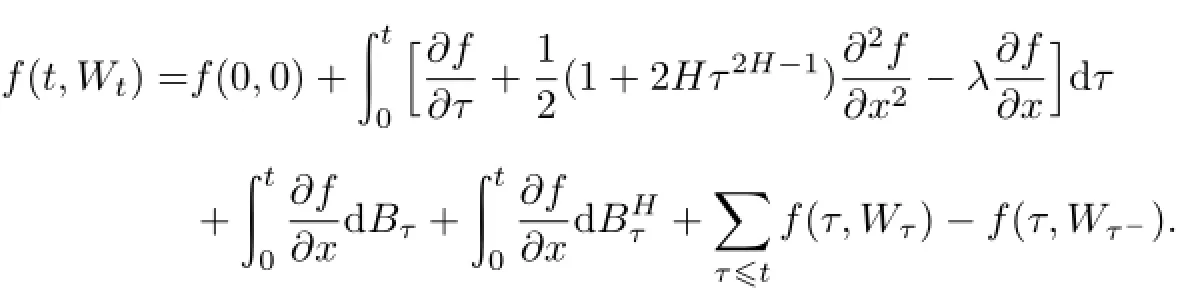
设g(φ)∈C2(R→R),又(dQt,dQt)=λdt,对g(Qt)应用广义积分[14],有
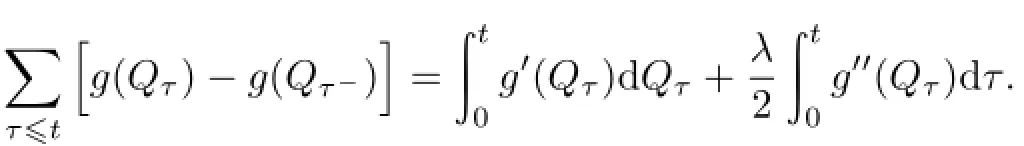
又Wt=Bt++Qt-λt,则

证明设Nt在ti时刻发生第i次跳跃.由于+Qt-λt,当i=1时,即Wt在(0,t)时刻只发生了一次跳,且跳时刻为t1,则在(0,t1)、(t1,t)内没有发生跳跃,那么由分数型公式可得
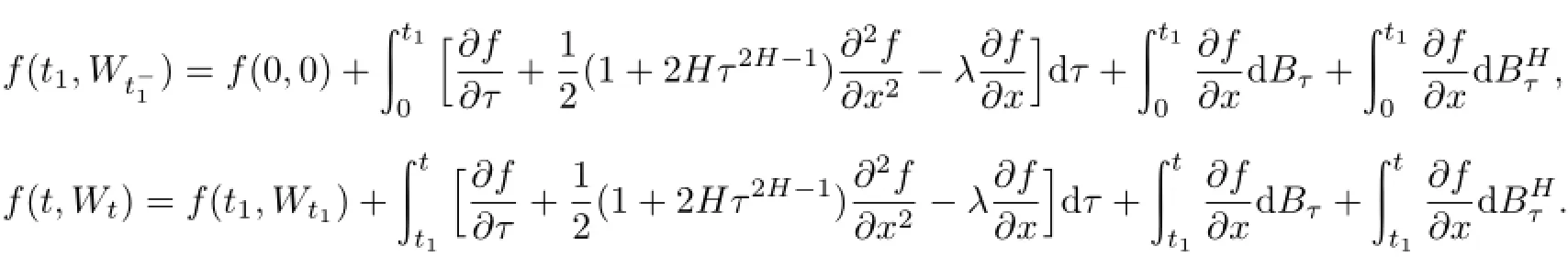
定理2随机微分方程(1)的解是
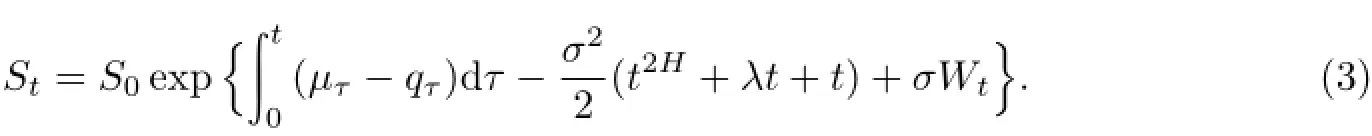
证明由定理1及定理2即可得证.
定理3假设标的资产价格St满足混合分数跳-扩散过程(1),则执行价格为K、到期日为T的几何平均亚式看涨期权在t(0≤t≤T)时刻的价值Vc(t,Jt,St)满足如下数学模型∶

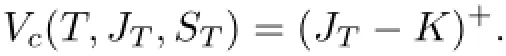
证明因为亚式期权是路径依赖型期权,几何平均亚式看涨期权在t时刻的价值V= Vc(t,Jt,St)不仅依赖于时间和标的资产的价格还依赖于路径Jt,资产价格在[0,t]上的几何平均值,则
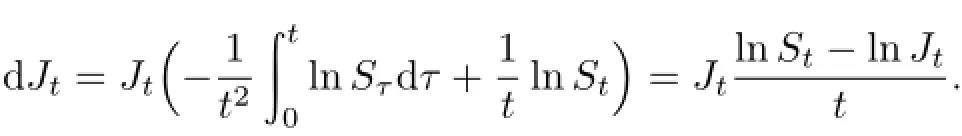
假设在金融市场中有一种债券和一种股票,债券和股票的价格分别满足下列微分方程∶
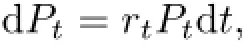

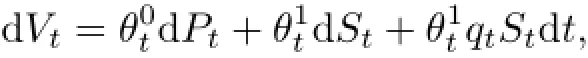
由自融资交易策略,有

由定理1和定理2,有
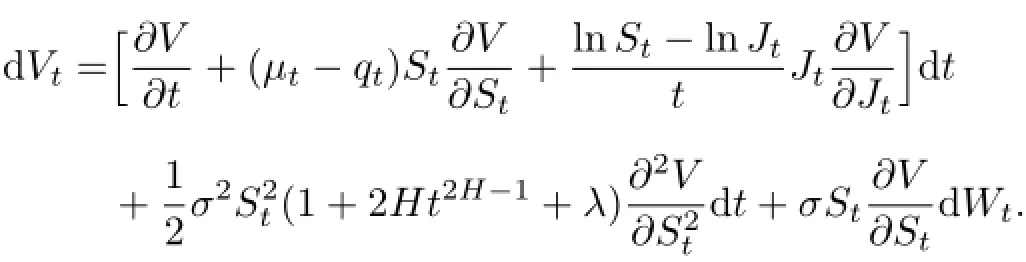
由于期权的价值与构造的投资组合的价值相等,故
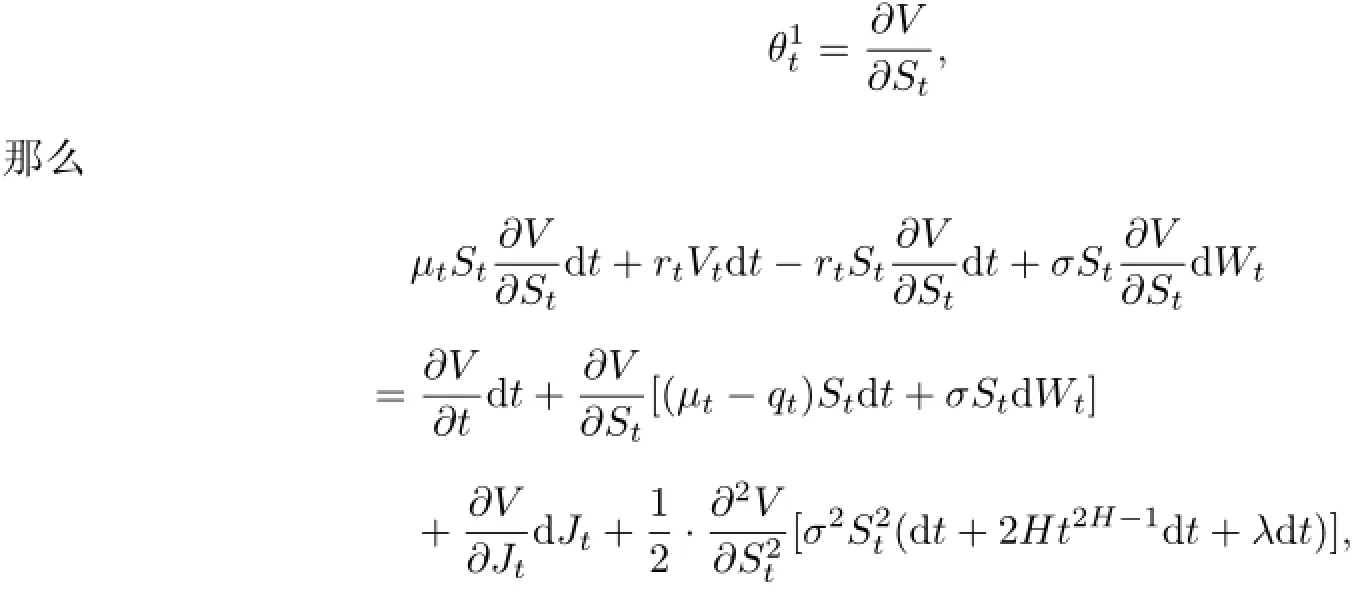
即rtVtσ2(1+2Ht2H-1+λ).则上式变为
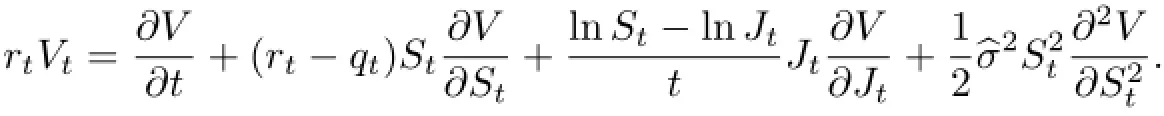
2 模型求解
定理4假设标的资产价格St满足混合分数跳-扩散过程(1),则执行价格为K、到期日为T的几何平均亚式看涨期权在t(0≤t≤T)时刻的价值Vc(t,Jt,St)为
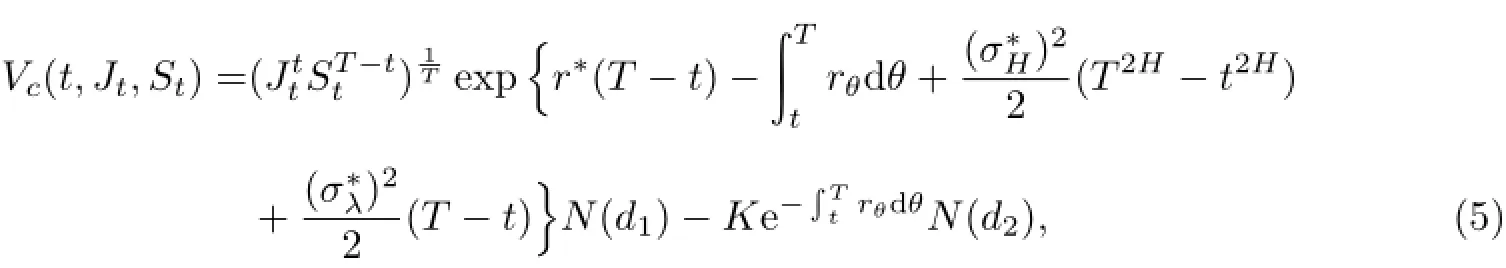
其中
2.3快速房颤患者的房颤患者和肽素与pro-BNP水平呈正相关,Pearson相关系数为0.610(P=0.000)
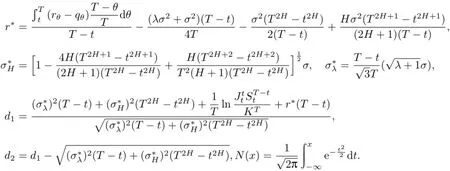
证明由定理3知,几何平均亚式看涨期权在t(0≤t≤T)时刻的价值Vc(t,Jt,St)满足模型(4).令

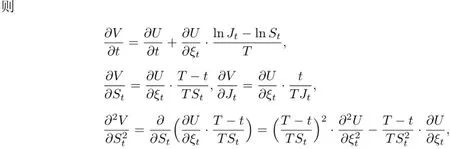
那么模型(4)转化为

其中α(t),β(t),γ(t)为待定函数,则

代入(6)式,整理后得
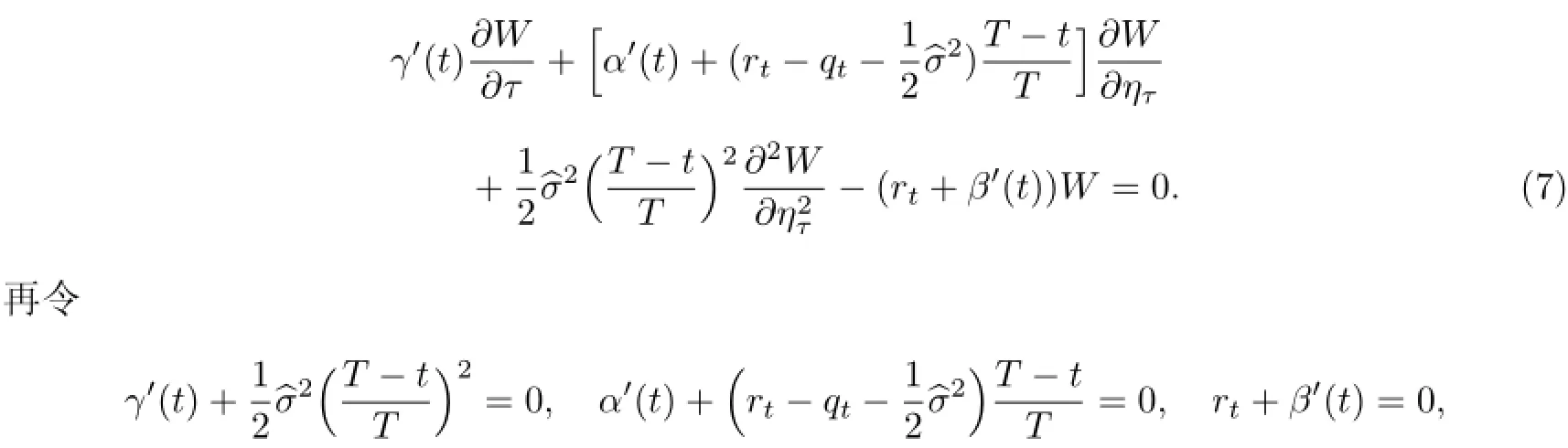
结合终止条件α(T)=β(T)=γ(T)=0,解得

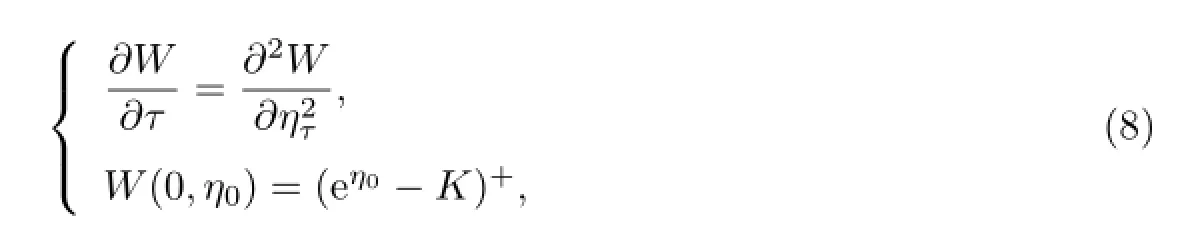
由热传导方程经典解理论可知,(8)式的解为

故(8)式的解为
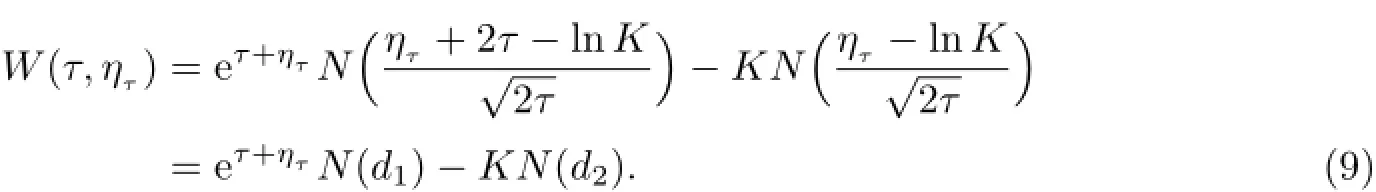
变量还原后有
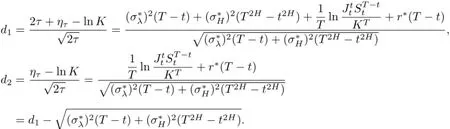
推论1假设标的资产价格St满足混合分数跳-扩散过程(1),则执行价格为K、到期日为T的几何平均亚式看跌期权在t(0≤t≤T)时刻的价值Vp(t,Jt,St)为
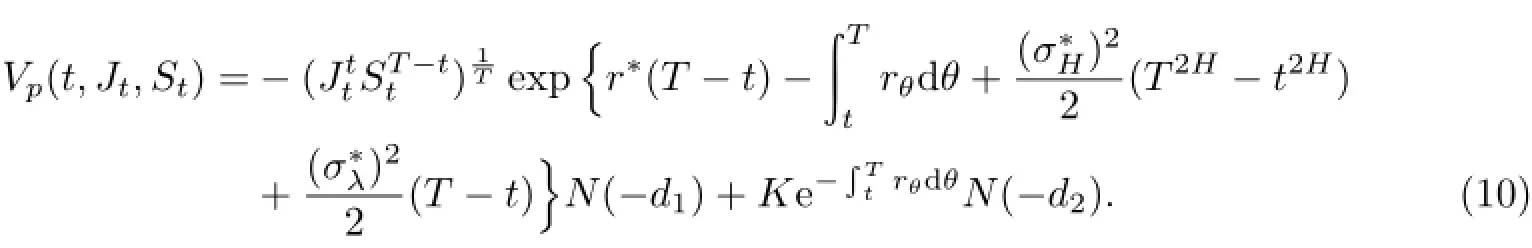
其他符号与定理4一致.
证明由边值条件V(T,JT,ST)=(K-JT)+,运用定理3中的方法求解方程(4)得到看跌期权的价值Vp(t,Jt,St).
3 数值实验
根据定理4中的定价公式进行数值实验,讨论定价公式中的各个参数对期权价值的影响.考虑一只标的资产为股票的亚式期权,其标的股票价格服从混合分数跳-扩散过程(1).假设股票的当前价格S=80元、期权的敲定价K=80元、股票价格的年波动率σ=0.4、无风险年利率r=0.05、红利率q=0.01,即对定理给出的亚式期权在t时刻的价值,考虑当其他参数不变时该期权的价值随其中某一参数变化的情况.对于亚式看跌期权,参数假设与看涨期权一致.在不同赫斯特指数下和标的股票价格下的亚式看涨、看跌期权价值的关系如图1,在不同跳跃强度下和标的股票价格下的亚式看涨、看跌期权价值的关系如图2.从图1中可以看出赫斯特指数与亚式看涨、看跌期权的价值成反比,且对亚式期权价值的影响幅度随着标的资产的减小而减小.从图2中可以看出跳跃强度与亚式看涨、看跌期权的价值成正比且跳跃强度对亚式看涨期权价值的影响程度比对亚式看跌期权价值的影响程度小.

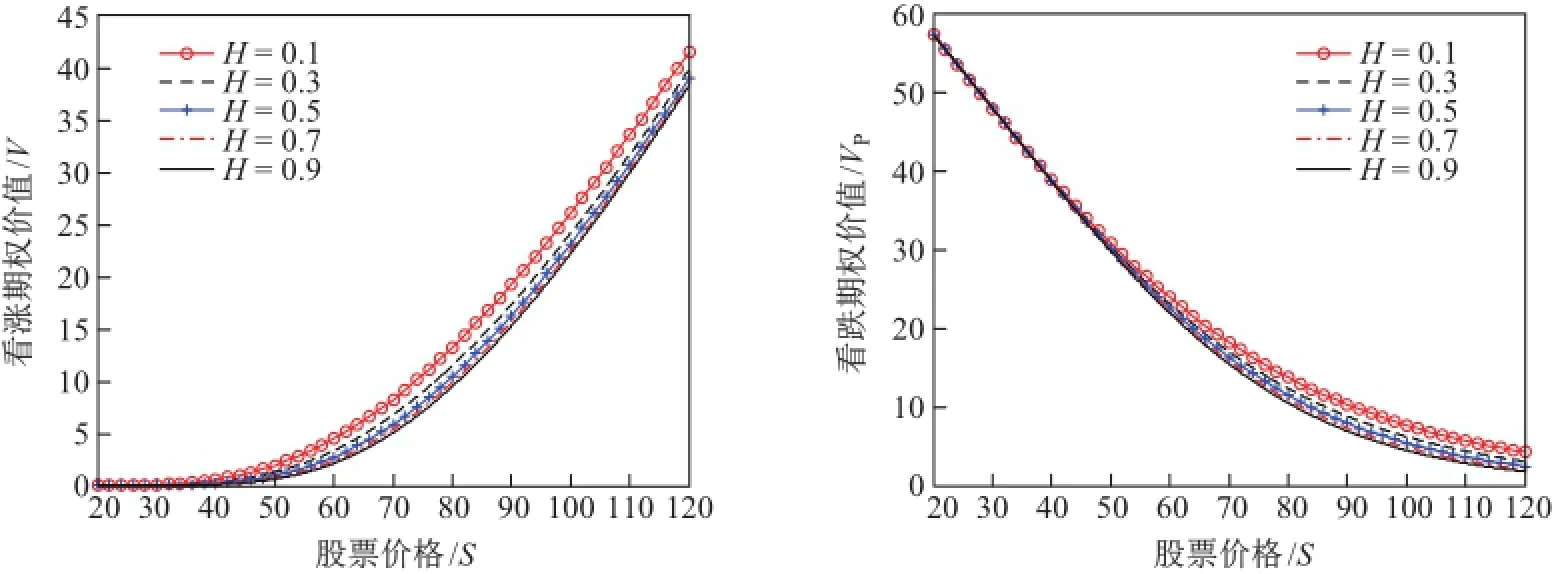
图1 对应不同H值的亚式期权价值Fig.1 Asian option pricing corresponding to different H
在参数假设取值不变的情况下,图3给出了到期期限和赫斯特指数同时变化时亚式看涨、看跌期权价值的走势情况,图4给出了到期期限和跳跃强度同时变化时亚式看涨、看跌期权价值的走势情况.由图3、图4可知,随着期权期限的增加,期权的价值也在不断增加,与实际情况相符.
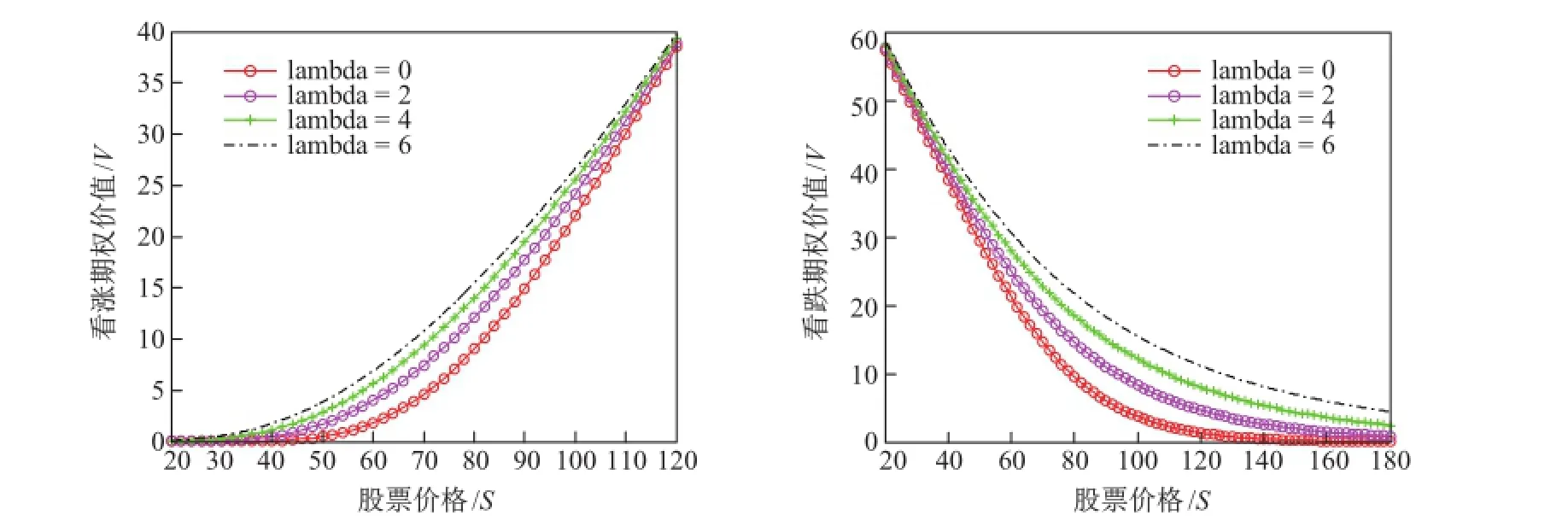
图2 对应不同λ值的亚式期权价值Fig.2 Asian option pricing corresponding to different λ
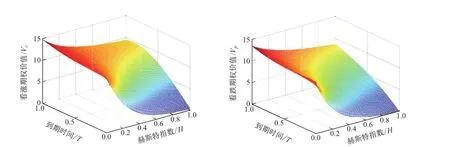
图3 赫斯特指数、到期时间和亚式期权价值的关系Fig.3 The relation of Hurst exponent,expiry date and Asian option
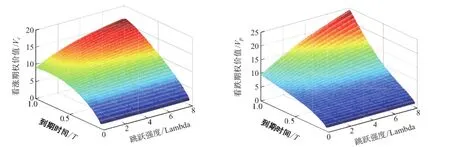
图4 跳跃强度、到期时间和亚式看涨期权价值的关系Fig.4 The relation of jump intensity,expiry date and Asian option
4 结论
本文假设股票价格满足混合分数跳-扩散过程,通过Itˆo引理和自融资交易策略推导出混合分数布朗运动下带跳的亚式期权的定价模型,再运用变量替换法对定价模型进行求解,得到几何平均亚式期权的解析解.通过数值实验可以看出赫斯特指数与跳跃强度对亚式期权价值有明显的影响.
[1]KEMNA A G Z,VORST A C F.A pricing method for options based on average asset values[J].Journal of Banking and Finance,1990,14(1):113-129.
[2]WONG H Y,CHEUNG H L.Geometric Asian options:Valuation and calibration with stochastic volatility[J]. Quantitative Finance,2004,4(3):301-314.
[3]CHOU C S,LIN H J.Asian options with jumps[J].Statistics&Probability,2006,6(14):1983-1993.
[4]CHERIDITO P.Regularizing fractional Brownian motion with a view towards stock price modelling[D].Z¨urich: Swiss Federal Institute of Technology,2001.
[5]CHERIDITO P.Arbirage in fractional Brownian motion models[J].Finance and Stochastics,2003,7(4):533-553.
[6]KUZNETSOV Y A.The absence of arbitrage in a model with fractal Brownian motion[J].Russian Mathematical Surveys,1999,54(4):847-848.
[7]Z¨AHLE M.Long range dependence,no arbitrage and the Black–Scholes formula[J].Stochastics and Dynamics, 2002,2(2):265-280.
[8]MISHURA Y S.Stochastic Calculus for Fractional Brownian Motion and Related Processes[M].Berlin:Springer, 2008.
[9]WANG X T.Scaling and long-range dependence in option pricing I:Pricing European option with transaction costs under the fractional Black–Scholes model[J].Physica A,2010,389(3):438-444.
[10]WANG X T.Scaling and long-range dependence in option pricing V:Multiscaling hedging and implied volatility smiles under the fractional Black–Scholes model with transaction costs[J].Physica A,2011,390(9):1623-1634.
[11]MEHRDOUST F,SABER N.Pricing arithmetic Asian option under a two-factor stochastic volatility model with jumps[J].Journal of Statistical Computation and Simulation,2015,85(18):3811-3819.
[12]RAMBEERICH N.A high order finite element scheme for pricing options under regime switching jump dif f usion processes[J].Journal of Computational and Applied Mathematics,2016,300(2):83-96.
[13]XIAO W L.Pricing currency options in a fractional Brownian motion with jumps[J].Economic Modelling,2010, 27(5):935-942.
[14]PENG B.Pricing Asian power options under jump-fraction process[J].Journal of Economics,Finance and Administrative Science,2012,17(33):2-9.
[15]丰月姣.带跳混合分数布朗运动下利差期权定价[J].佳木斯大学学报(自然科学版),2013,30(6):922-925.
[16]孙玉东.带跳混合分数布朗运动下利差期权定价[J].系统科学与数学,2013,32(11):1377-1385.
[17]SHOKROLLAHI F.Actuarial approach in a mixed fractional Brownian motion with jumps environment for pricing currency option[J].Advances in Dif f erence Equations,2015,257(1):1-8.
(责任编辑:林磊)
Pricing Asian option under mixed jump-fraction process
GENG Yan-jing,ZHOU Sheng-wu
(Department of Mathematics,China University of Mining and Technology, Xuzhou Jiangsu221008,China)
This paper mainly studied the geometric average Asian option pricing on the condition that the underlying asset followed mixed jump-fraction process.The general Itˆo’s lemma and the self-f i nancing dynamic strategy were obtained by using the partial differential equation of such option pricing in the mixed fractional environment with jump. With the combination of boundary condition,an analytic formula for the geometric average Asian option was derived by solving the partial differential equation.The numerical experiments were showed to discuss the inf l uence of different parameters on the option value.The results were the generalization of some existing results which was closer to the real f i nancial market.
mixed jump-fraction process;geometric average Asian option;partial differential equation
O211.6
:A
10.3969/j.issn.1000-5641.2017.03.003
1000-5641(2017)03-0029-10
2016-06-23
中央高校基本科研业务费专项资金(2013XK03)
耿延静,女,硕士研究生,研究方向为金融数学.E-mail:gengyanjing ah@qq.com.
周圣武,男,教授,研究方向为金融数学.E-mail:zswcumt@163.com.

