软合并协作频谱感知中吞吐量的优化
郭 超,张政保,姚少林,刘广凯
(1.解放军71777部队,山东 济南 250100;2.解放军军械工程学院,河北 石家庄 050003;3.电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003)
软合并协作频谱感知中吞吐量的优化
郭 超1,张政保2,姚少林3,刘广凯2
(1.解放军71777部队,山东 济南 250100;2.解放军军械工程学院,河北 石家庄 050003;3.电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003)
针对认知无线电网络中认知用户接收信噪比存在差异情况下吞吐量的优化问题,提出了基于吞吐量的软合并协作频谱感知优化方法。根据不同融合参数对认知用户吞吐量的影响,该方法首先对吞吐量方程进行了简化,其次当认知用户按照信噪比大小向融合中心发送检测统计量时,运用最优停止法确定唯一的检测时间和协作用户数,使认知用户的吞吐量取得最大值。仿真结果表明,与随机上传以及等增益软合并方法对比,软合并协作频谱感知优化算法可以显著提高认知用户吞吐量。
协作频谱感知;软合并;最优停止准则;吞吐量
0 引言
针对当前通信网中出现的频谱拥挤、空闲频谱未有效利用的情况,认知无线电(CognitiveRadio,CR)通过允许认知用户(CognitiveUser,CU)接入空闲信道的方式,实现频谱资源的高效利用[1-2]。频谱感知作为CR的关键技术,如何提高频谱感知性能成为了CR技术的焦点。在认知网络中,阴影效应和多径衰落严重影响该网络中单节点频谱感知的性能,通过多个CU相互协作能够有效解决这一问题[3]。为了确定主用户(PrimaryUser,PU)是否占用信道,Liang等人提出了先感知再传输的帧结构模型[4-5]。研究表明,增加CU数目和感知时间能够提高检测性能,但是减少了CU传输数据的时间。因此,仅仅以检测性能作为检测目标不能保证CU的数据传输。在PU充分保护的情况下,以最大化CU吞吐量作为系统目标函数能更有效地利用频谱资源。
CR网络中集中式协作频谱感知的融合方式分为硬判决和软判决两种。硬判决不需要专门的控制信道,但是软判决比硬判决具有更好的性能[6]。文献[7-8]分别提出了等增益合并和最大比合并。文献[9]通过设置软合并融合参数最小化干扰容量和最大化吞吐量,但是并未考虑感知时间和本地检测数据上传时间对吞吐量的影响。文献[10]针对集中式软合并模型,证明了感知时间是吞吐量的凸函数。文献[11]采用新的CR帧结构,假设其他CU可以利用当前CU的上传时间进行频谱感知,但是忽略了系统之间的同步性,实现难度较大。文献[12]通过优化融合准则,使系统吞吐量达到最大,但假设CU采用固定的感知时间。在文献[10-12]中,均假设所有的CU具有相同的信噪比,但在实际无线电环境中,不同协作用户之间信噪比存在较大差异。本文在上述文献的基础上,考虑不同CU之间信噪比存在差异,提出了基于吞吐量的最大比软合并协作频谱感知的优化算法。
1 系统模型
考虑CR网络中包含M个CU节点,1个FC。第i个CU接收信号为:
(1)
n=1,2,…,N;i=1,2,…,M
式(1)中,yi(n)为第i个用户接收到的第n个信号采样值,si(n)为PU发送信号,zi(n)表示噪声,且都为实值高斯信号。假设PU信号和噪声相互独立。在本地检测过程中,CU不能获得PU的任何先验知识。H0表示PU信号不存在,H1表示PU信号存在。应用能量检测进行单节点频谱感知,检测统计量为:
(2)
当采样点足够大时,统计量T服从高斯分布[3]。
式(3)中,γi为第i个CU接收的信噪比,N为进行能量检测时采样点数,等于感知时间和采样频率的乘积,σ2为噪声方差。
FC接收到m个CU发送的本地检测信息,并将各个CU本地检测统计量Ti(y)按照一定的权重ωi进行累加。根据高斯分布的性质,累加统计量同样服从高斯分布:
(4)
(5)
当检测门限一定时,虚警概率和检测概率分别表示为:
(6)
(7)
式中,λ′=λ/σ2。本文按照信噪比大小选择权重系数[8],并且满足‖ω‖=1。
(8)
2 系统吞吐量及最优停止法
2.1 认知用户吞吐量
集中式软合并系统模型如图1所示,帧长T被分为感知时间、融合时间和传输时间三部分[12]。为了满足CU同步性要求,CU用相同的时间进行频谱感知,假设一个CU上传本地检测量时,另外的用户不能进行频谱感知[13]。假设在感知时间内,PU状态不发生变化。

图1 软合并系统帧结构框图Fig.1 Frame duration illustration of soft combination
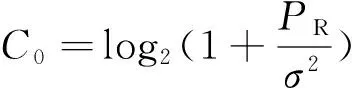
s.t.Pd≥Pd,th,0≤τ≤T-mτ0,1≤m≤M
(9)
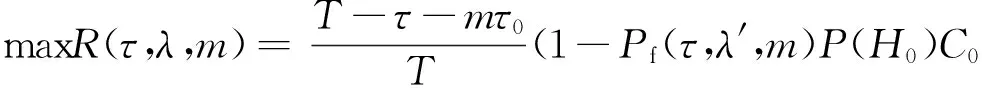
s.t.Pd=Pd,th,0≤τ≤T-mτ0,1≤m≤M
(10)
(11)
由Pf和Pd的关系式可得:
(12)
因此,P2问题可转化为优化方程P3:
s.t.0≤τ≤T-mτ0,1≤m≤M
(13)
2.2 最优停止法
最优停止理论在研究序贯决策问题上具有广泛应用[14]。集中式软判决协作频谱感知网络中,CU的吞吐量和CU本地检测信息融合次序、协作用户数以及感知时间有关。最优停止理论可以用来寻找最优的感知时间和协作用户数。本文中各个CU首先用相同的感知时间进行频谱感知,CU统计信息上传顺序为CU接收PU信噪比降序序列,CU按照信噪比大小顺序对本地检测信息进行融合。为了确定上传顺序,假设在一帧时间内,CU用户接收到的信噪比保持不变。CU通过低速控制信道将CU的信噪比传输至FC[15]。
FC对m个本地检测信息进行最大比合并,并与恒检测概率确定的检测门限进行判决,从而确定向FC传输数据的个数。根据最优停止理论,观察序列和收益序列定义如下:
观察序列:Xm=0表示第m个CU信息未被融合,Xm=1表示第m个CU被用来融合。
(14)
收益序列:有m个CU按照信噪比大小依次对本地检测统计量进行融合,收益序列为:
(15)
(m+1)个CU期望收益为
(16)
最优停止准则:当R(m)≥E(R(m+1)时,可得到最大吞吐量时的CU数,否则继续进行融合判断,停止准则为:
(17)
文献[9]证明了软合并中存在最优的感知时间使吞吐量达到最大。其中,τ*为m个用户时最优的感知时间,比较第(m+1)个CU发送信息给FC的预期收益与第m个CU发送信息给FC实际收益。
ΔRm+1=E(R(τ,m+1)-R(τ*,m)
(18)
优化问题P3可转化为P4:
maxΔRm
s.t.0≤τ≤T-mτ
(19)
为了对上式进行求解,确定最优的感知时间和协作用户数。需要对解的个数以及唯一性进行探讨。
定理1:当CU数m一定时,感知时间τ是ΔRm的凸函数。
证明:根据凸优化理论,当ΔRm满足以下三个条件时,即可证明定理1。


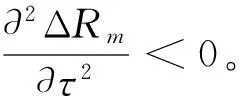
条件1)、2)证明:求ΔRm关于τ的一阶偏导数,可得:
(20)

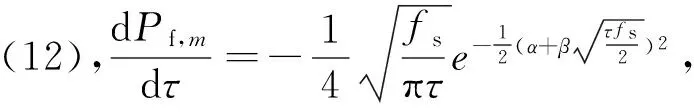
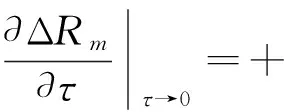
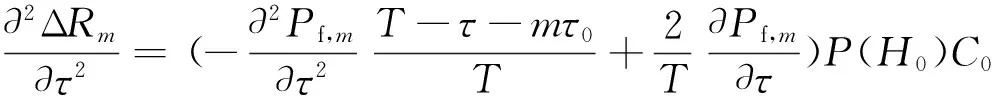
根据定理得证,即对于第m个CU存在最优的感知时间使得ΔRm取得最大值,可以采用经典的精确线搜索方法求得最优值,例如黄金分割法求得最优感知时间[16]。
定理2:CU以接收信号的信噪比大小逐个向FC传输数据,最优准则为式(17),则存在参与融合的最优的CU数,且是唯一的。
ΔRm对γm求导可得:
(21)

(22)
2.3 算法步骤
步骤一:FC根据接收到信噪比大小确定融合次序。
步骤二:初始化,令m=1,利用黄金分割法求出m=1时最优感知时间,计算实际收益和m=2时的期望收益。
步骤三:利用最优停止理论求得ΔRm最大值,求出相应的感知时间τ′,比较ΔRm与0的大小。
步骤四:如果ΔRm>0,令m=m+1。返回步骤三。
步骤五:当ΔRm≤0时,停止搜索,可确定最优用户数(m-1)以及最优感知时间τ′。
CU按照信噪比大小向FC传输本地检测统计量,根据最优停止法,可以确定最优感知时间和感知用户数。采用该方法设置参数,能够保证PU在不受干扰的条件下,使CU的吞吐量达到最大。
3 仿真实验
在仿真试验中,假设CU发射功率为1 W,噪声功率为0.01 W, 道带宽为1 MHz,采样频率为2 MHz,主信信道的空闲概率为0.8,帧长为30 ms。每个CU向FC传输数据时间为0.8 ms。检测概率门限设为0.9,由于CU之间路径损耗以及衰落不同,信噪比存在差异。
图2是协作CU分别为1到7时,感知时间和m个CU的最大吞吐量以及(m+1)个CU期望吞吐量差值ΔRm的关系图。其中CU接收到的信噪比分别为-15~-21 dB,间隔为1 dB依次递减。从图2中可以看出,感知时间是ΔRm的凸函数,随着感知时间的增加,吞吐量先变大再变小,证明了定理1的正确性。随着信噪比的减小ΔRm逐渐递减,证明了定理2的正确性。当CU数为4时ΔRm<0,因此存在最优的感知时间和协作用户数使系统的吞吐量达到最大。
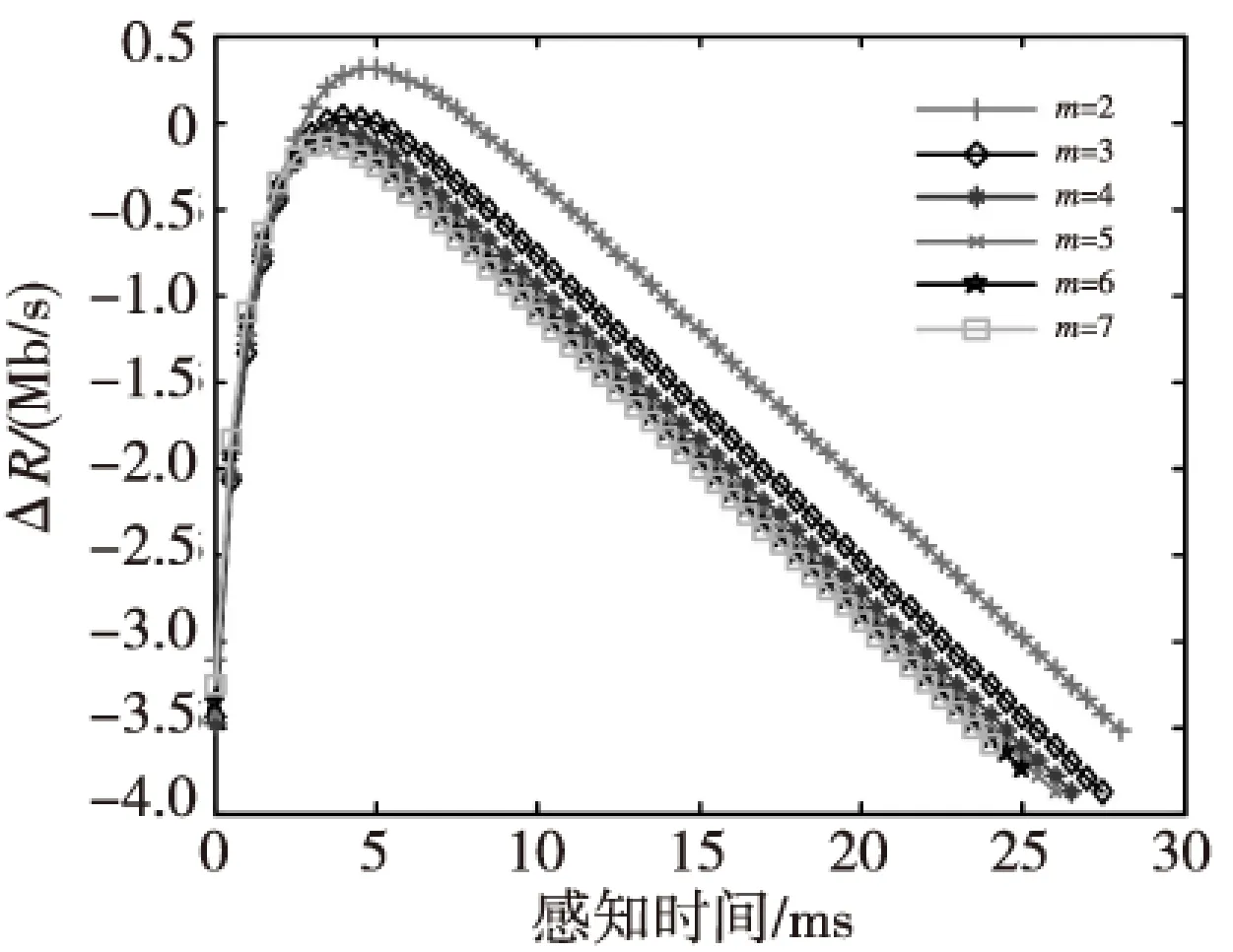
图2 感知时间和ΔRm关系Fig.2 ΔRmversus from sensing time
图3给出了R(m)和E(R(m+1)在不同协作用户数时的值,CU信噪比同样是-15~-21 dB,从
图中可以看出,当协作用户数为3时,感知时间为4.1 ms,吞吐量达到最大值3.93 Mb/s。其中R1(m),E(R1(m+1))以及E(R2(m+1))和R2(m)分别表示FC按照等增益方式进行合并以及CU采用随机上传本地检测量时m个CU吞吐量和m+1个CU的预期吞吐量。图中显示,采用本文最大比合并和等增益合并吞吐量相差不大,这是因为仿真时CU间的信噪比差选为1 dB,相差较小。此外,从图中正可以看出本文算法明显优于随机上传算法,并且随机上传方法最优,CU数不唯一。
图4是当CU数为5时,CU接收信噪比间隔和系统吞吐量关系图。CU接收信噪比间隔为Δγ=γ1-aB,其中,γ1=-15 dB,B={0,1,2,3,4},a表示信噪比差值。从图中可以看出,随着信噪比间隔增大,最大比合并比等增益合并具有更大的吞吐量。图5表示的是CU数目为5,CU之间信噪比间隔分别为0~6 dB,从图中可以看随着CU之间的信噪比差值越来越大,吞吐量减小,这是因为参与感知的CU的信噪比降低。
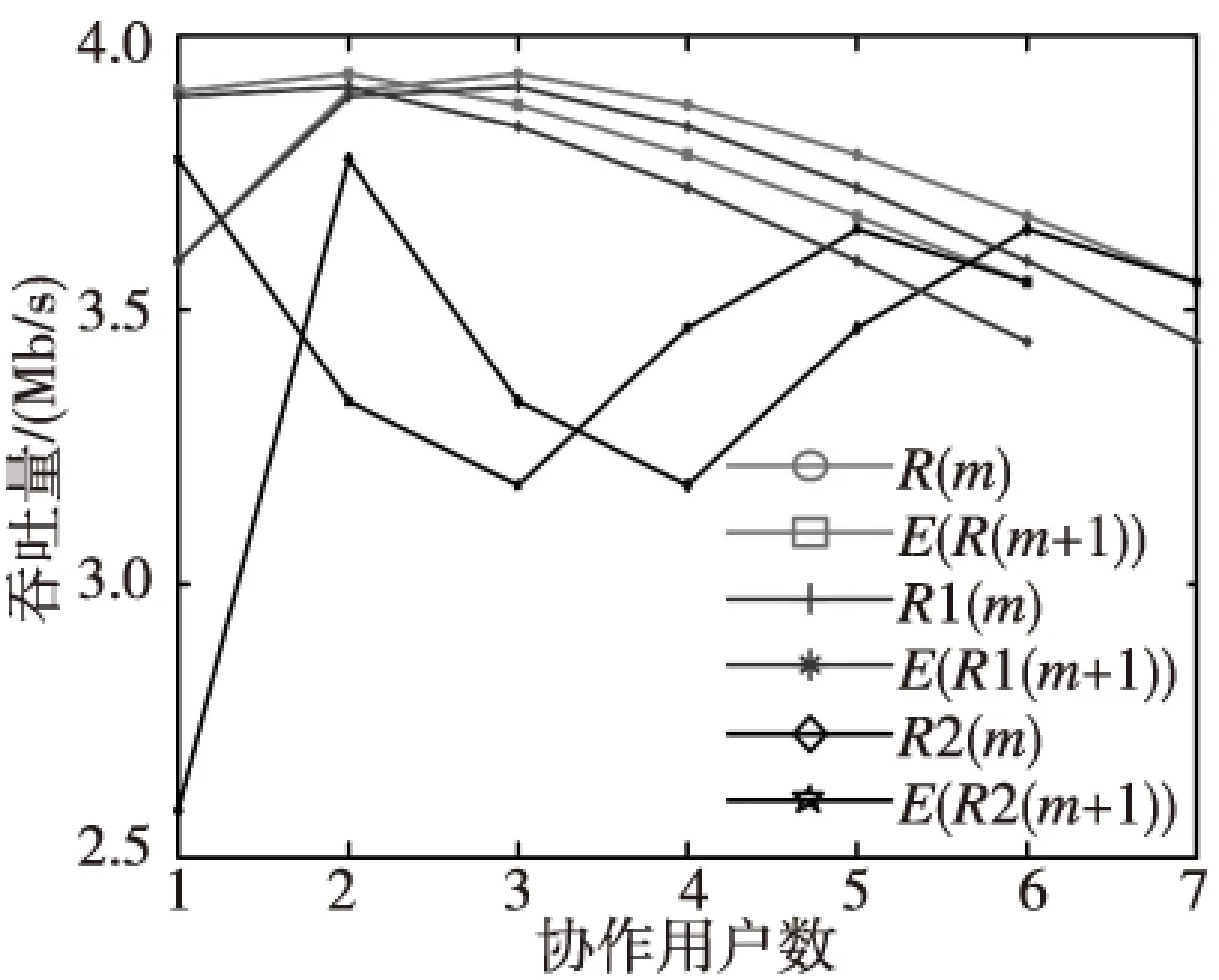
图3 不同协作用户和最大吞吐量关系Fig.3 The maximal throughput versus from cooperative users
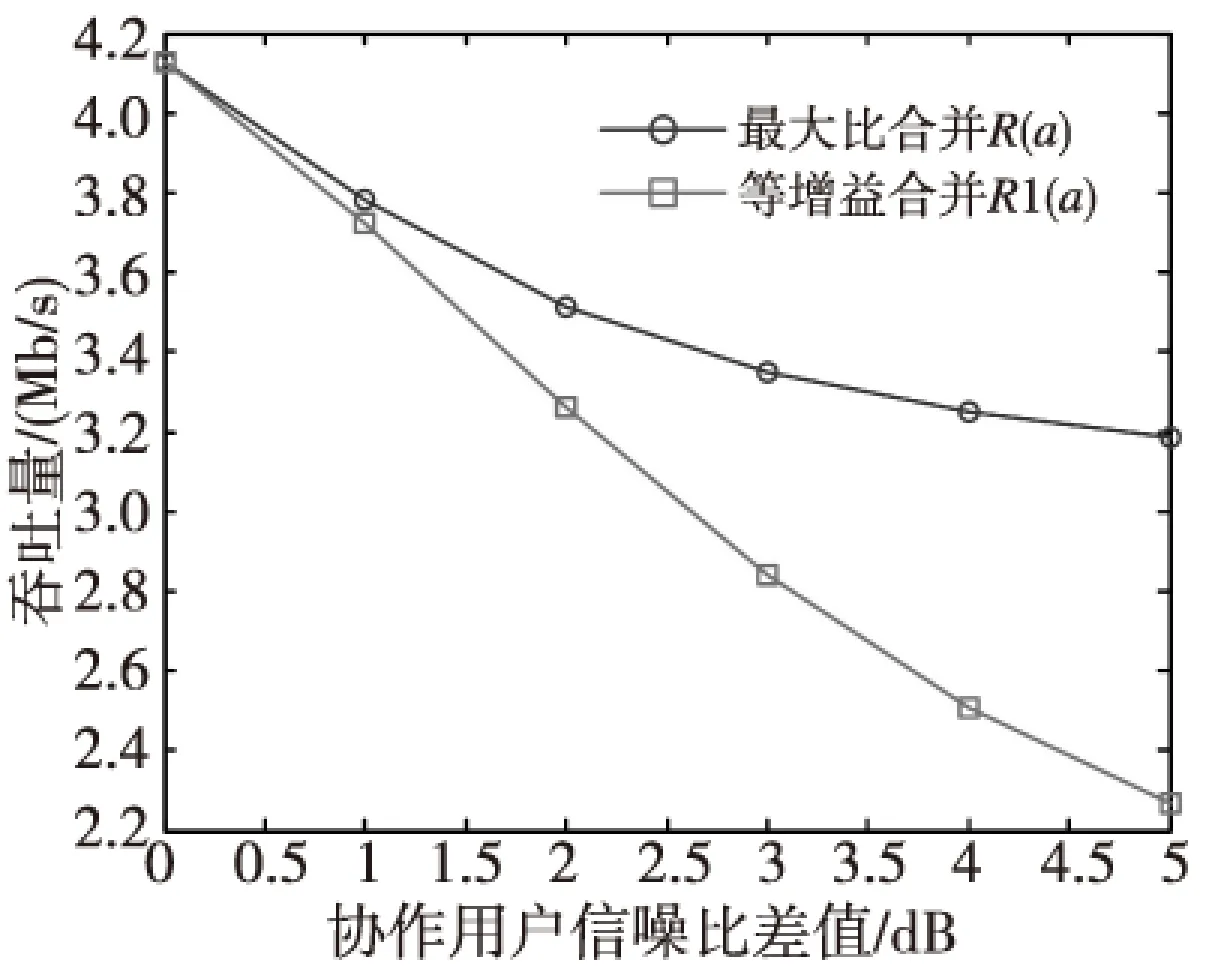
图4 协作用户间信噪比差值和吞吐量关系Fig.4 The throughput versus fromdifference of the CUs adjacent SNR

图5 不同协作用户间信噪比差值条件下感知时间吞吐量关系Fig.5 The throughput versus sensing time in the condition ofdifferent CUs adjacent SNR
图6、图7分别表示检测概率门限值、单个CU上传本地检测时间对吞吐量的影响。其中,参与协作的CU数目为10,信噪比范围为-15~-24 dB,信噪比间隔为1 dB。从图6可以看出,检测概率门限值越高,对PU干扰越小,但CU的吞吐量也随之减小,验证了优化问题P1转化为P2的正确性。图7显示上传本地检测统计量T0时间越长,系统吞吐量越小。图8表示的是当取最优感知时间时,单个CU传输时间不同对最大吞吐量的影响,从图中可以看出本文算法明显优于等增益合并算法。因此在满足传输CU本地检测量地条件下,应选择更小的上传时间。
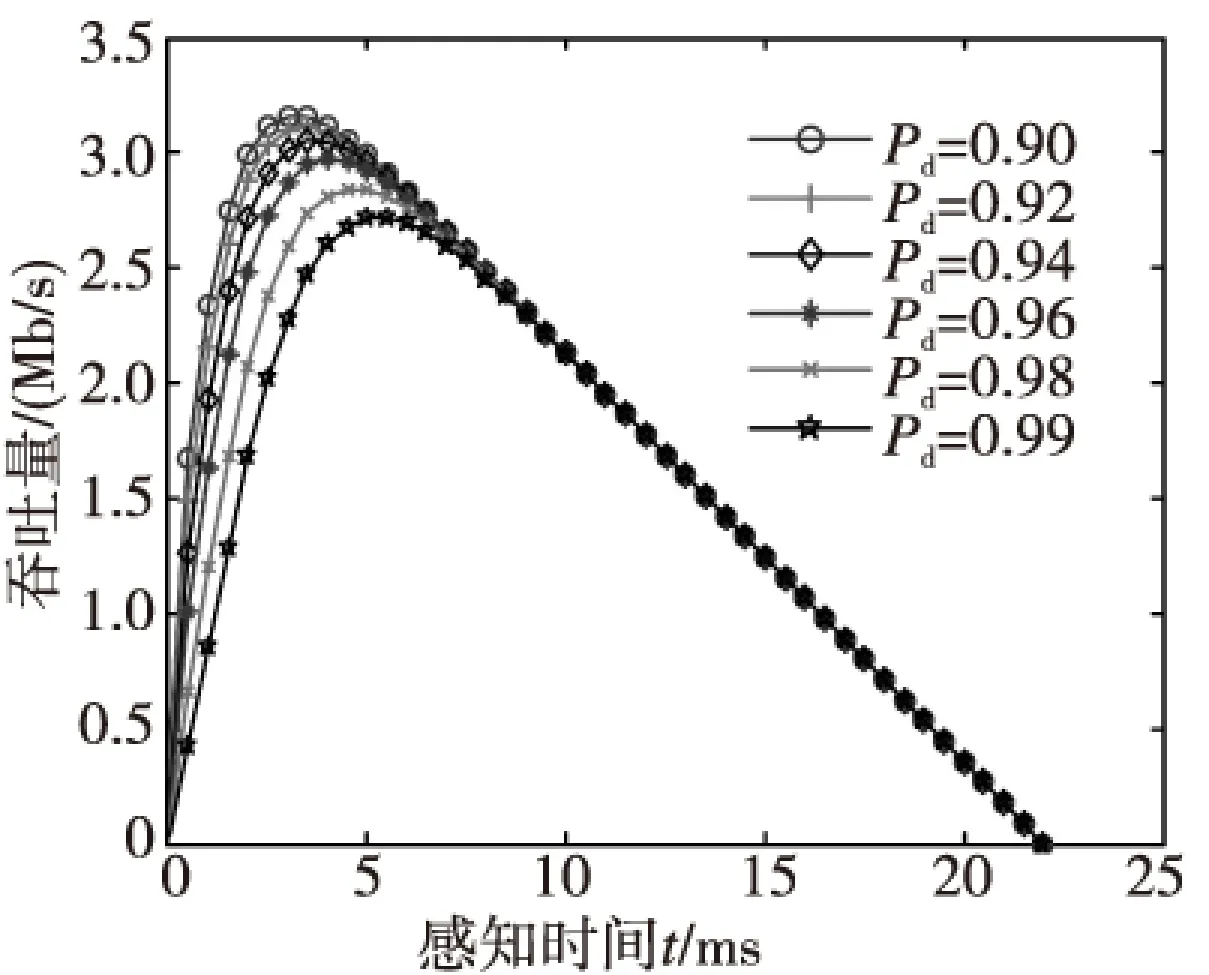
图6 不同检测概率门限条件下感知时间吞吐量关系Fig.6 The throughput versus sensing time in the condition of different detection probability threshold

图7 单个用户传输时间不同条件下感知时间吞吐量关系Fig.7 The throughput versus sensing time in the condition ofdifferent transmission time of signal CU

图8 单个CU传输时间和不同融合策略吞吐量关系Fig.8 The throughputof different fusion scheme versus signal CU transmission time
4 结论
本文提出了CR网络中软合并协作频谱感知吞吐量优化方法。该方法应用最优停止法理论,CU按照信噪比大小向FC传输本地检测统计量,证明了CU系统吞吐量是感知时间的凸函数,并且存在唯一的协作用户数使得系统吞吐量达到最大值。仿真分析了不同协作用户之间的信噪比差值、检测概率门限值、CU上传本地信息量时间对吞吐量的影响。并与CU随机上传本地检测统计量以及等增益软合并方法对比,仿真实验表明本文提出算法能够明显提高CU吞吐量。
[1]Akyildiz I F, Lee N Y, Vuran M C, et al.A survey on spectrum management in cognitive radio networks[J].IEEE Communications Magazine,2008, 46(4):40-48.
[2]吕春英,沈国勤,袁誉红,等.基于簇加权的协作频谱感知算法[J].探测与控制学报,2012,34(2):72-76.
[3]Fan R, Jiang H, Guo Q,et al.Joint optimal cooperative sensing and resource allocation in multichannel cognitive radio networks[J].IEEE Transactions on Vehicular Technology,2011, 60(2): 722-729.
[4]Liang Y C,ZENG Y H, PEH E, et al. Sensing-throughput tradeoff for cognitive radio networks[J]. IEEE Transactions on Wireless Communications,2008,7( 4) : 1326-1336.
[5]Liang YingChang, Guan YongLiang, Zeng Yonghong, et al.Optimization of cooperative sensing in cognitive radio networks: a sensing-throughput tradeoff view[J]. IEEE Transactions on Vehicular Technology,2009,58(9) :5295-5299.
[6]Masoud Moradkhani, Paeiz Azmi, Mohammad Ali Pourmina.Optimized Reliable Data Combining CooperativeSpectrum Sensing Method in Cognitive Radio Networks[J].Wireless PersCommun ,2014,74(2):569-583.
[7]Frank Visser,Gerard J M Janssen,Przemyslaw Pawelczak,et al.Multinode spectrum sensing based on energy detection for dynamic spectrum access[C]// Proceedings of the 67th vehicular technology conference(VTC-Spring’08) , Singapore.IEEE,2008: 1394-1398.
[8]Wu S W, Zhu J K, Qiu L.SNR-based Weighted Cooperative Spectrum Sensing in Cognitive Radio Networks[J] Journal of China Universities of Posts and Telecommunications,2010, 17(2): 1-7.
[9]LIU Xin,TAN Xuezhi,ZHAO Ying.Comperative Spectrum sensing Algorithm with soft Fusion Based on Weighting[J].Journal of applied sciences.2013,31(2):116-122.
[10]张雯, 杨家玮, 闫琦,等.采用软合并合作检测的认知无线电系统的吞吐量优化[J].西安电子科技大学学报(自然科学版),2010,37(6):987-992.
[11]Hu Hang, Xu Youyun, Li Ning .Optimization of Time-Domain Combining Cooperative Spectrum Sensing in Cognitive Radio Networks[J].Wireless Personal Communications,2013,72(4): 2229-2249.
[12]Li Shuang ,Zheng Zizhan, Ekici Eylem, et al.Maximizing System Throughput by Cooperative Sensing in Cognitive Radio Networks[J].IEEE IEEE/ACM TRANSACTIONS ON NETWORKING,2014,22(4):1245-1256.
[13]Yang Chao, Fu Yuli, Zhang Yan, et al.An efficient hybrid spectrum access algorithm in OFDM-based wideband cognitive radio networks[J].Neurocomputing,2014,125:33-40.
[14]FERGUSON TS.Optimal Stopping and Applications[M/OL].2006[2012-09-27].http://www.math.ucla.edu/~tom/stooping/contents.ht.
[15]Hesham L, Sultan A, Nafie M, et al.Distributed spectrum sensing with sequential ordered transmissions to a cognitive fusion center[J].IEEE Transactions on Signal Processing,2012, 60(5): 2524-2538.
[16]马昌凤,柯艺芬,谢亚君.最优化计算方法及其 MATLAB 程序实现[M].北京:国防工业出版社, 2015.
Throughput Optimization in Cooperative Spectrum Sensing with Soft Combination
GUO Chao1, ZHANG Zhengbao2, YAO Shaolin3, LIU Guangkai2
(1.Unit 71777 of PLA, Jinan 250100, China; 2. Ordnance Engineering College, Shijiazhuang 050003, China;3. State Key Laboratory of Complex Electromagnetic Environment Effects on Electronic and Information System, Luoyang 471003, China)
In the condition that the receiving SNR of cognitive radio network are different, the throughput optimization method of cooperative spectrum sensing with soft combing was proposed in this paper. According to the effect of different parameters on the integration throughput, the throughput equation was simplified firstly. And then when fusion center fused the test statistic in the order of the cognitive users SNR, the optimal stopping criterion could be used to determine the unique optimal sensing time and cognitive number. Simulation results showed that the cooperative spectrum sensing with soft combing optimization method could dramatically improve system throughput comparing with the equal gain and random upload soft combination.
cooperative spectrum sensing; soft combination; optimal stopping criterion; throughput
2016-12-02
郭超(1991— ), 男,湖北十堰人,硕士,研究方向:认知无线电理论与技术。E-mail:guochaojunxie@163.com。
TN911
A
1008-1194(2017)02-0081-06

