三分量磁传感器倾斜放置时的磁场测量方法

张朝阳，衣 军，虞伟乔

(1．海军装备技术研究所，上海 200083；2．解放军91656部队，上海 200080)

三分量磁传感器倾斜放置时的磁场测量方法

张朝阳1，衣 军1，虞伟乔2

(1．海军装备技术研究所，上海 200083；2．解放军91656部队，上海 200080)

针对三分量磁传感器在使用时安装倾斜易引起较大测量误差的问题，提出了三分量磁传感器倾斜放置时的磁场测量方法。该方法采用三个等效姿态角α、β、γ表示传感器的倾斜姿态，建立转换矩阵对磁场测量值进行修正。在仅利用地磁场无法唯一确定姿态角的情况下，引入已知辅助磁场，形成第二背景磁场，通过PSO算法求出传感器的姿态角，然后利用转换矩阵对目标磁场三分量测量值进行修正。随机挑选了2个磁传感器进行实验验证，实验结果表明，传感器倾斜放置时目标磁场的测量值经该方法修正后的值接近目标磁场的真实测量值，能够满足实际工程应用的需要。

三分量磁传感器；磁场修正；PSO算法；姿态角；转换矩阵

0 引言

用三分量磁传感器测量三分量磁场是舰船消磁、磁性定位、地磁测量等领域的必要工作[1-5]。磁性目标的测量磁场，一般由测得的目标磁场与地磁场(背景磁场)的合成磁场减去地磁场得到。利用三分量磁传感器测量三分量磁场的一个关键问题就是磁传感器的放置状态。当磁传感器放置有倾斜时，其三个测量轴向与地磁坐标轴向均会出现偏差，此时若仍将测量值作为地磁坐标系中的磁场值，则会出现大的测量误差。舰艇上安装的三分量磁强计[2-3]、水下固定放置的三分量磁探头或安装在消磁站洞壁上三分量磁传感器等就很难保证理想的放置姿态，往往会有一定的倾斜，这时测量的三分量磁场值都将存在误差。另外，在实验室利用大量三分量磁传感器进行磁场测量时，特别是需要测量大量磁场三分量数据、不断变换传感器位置、传感器摆放紧凑不方便调整时，磁场三分量磁场的准确测量也是一个困难的问题。文献[6]曾就舰载三分量磁传感器的放置误差对舰船消磁系统控制信号的影响进行了分析，表明传感器放置误差给磁场三分量测量值造成的影响不能忽视。

目前解决三分量磁传感器倾斜放置时磁场测量问题的方法主要有两种：一种是对每个传感器进行调节，使传感器的三个轴与地磁坐标轴同向，直接得到准确的测量值，但这需要花费很大的力气，而且有时受条件限制无法调节准确；另一种方法是建立转换矩阵，对磁场测量值进行转换修正后得到准确的测量值，这种方法可以避免繁杂的传感器调整工作。目前在保证传感器垂直放置的情况下，可以通过简单的转换矩阵得到磁性目标准确的三分量磁场值，这种转换是基于当地地磁场水平分量的测量值进行的(下文将作讨论)，但当传感器发生倾斜时，仅通过地磁场无法得到转换矩阵的唯一解，利用第二种方法获得准确的目标磁场就成为一个难题。针对这一问题，本文提出了三分量磁传感器倾斜放置时的磁场测量方法。

1 传感器垂直放置时的磁场测量

传感器坐标系是指磁传感器自身三个测量轴构成的测量坐标系。传感器垂直放置时，向下为z轴正向，x轴，y轴按照右手螺旋定则在水平面分布。地磁坐标系中，磁北方向为x轴正向，磁东方向为y轴正向，向下为z轴正向。传感器所测得的目标磁场值是目标磁场在传感器三个测量轴上的投影，为了对所测得的磁场进行分析计算等[7-8]，需要将传感器坐标系下的磁场三分量测量值转化到固定的地磁坐标系中。在消磁、磁场分析等问题研究中，我们希望传感器能够处于理想的放置状态，即传感器坐标系的坐标轴(x′,y′,z′)能与地磁坐标系坐标轴(x,y,z)方向一致(如图1所示)，这样便可直接将所测得的目标磁场按照地磁坐标系与其他坐标系(如舰船坐标系)的关系进行转换，进行下一步的分析。

图1 同向的传感器坐标系与地磁坐标系Fig.1 The sensor's reference frame and geomagnetic reference frame with same direction

但一般情况下传感器坐标轴不一定能与地磁坐标轴方向一致，这样我们就必须花费大量的精力去调节传感器的三个轴向，但往往无法调节准确，所以我们通常采用建立转换矩阵的方法将传感器测量的目标磁场转换到地磁坐标系下。设某目标磁场在地磁坐标系下的值为(Bx,By,Bz)，在传感器坐标系下的测量值为(Bx′,By′,Bz′)，转换矩阵为Atrans，则有下面转换关系：

(1)

传感器垂直(z轴垂直向下)时的转换矩阵容易求出，但当传感器倾斜时，三轴方向不确定，转换矩阵Atrans则很难得到，下面首先对传感器垂直时的磁场测量作简要介绍。

传感器垂直放置时，z轴能够保持垂直向下，所测得的z分量目标磁场值就是地磁坐标系下的z分量值。但在水平面上传感器的坐标轴同地磁坐标轴往往存在一定的夹角，如图2所示，设传感器x(y)轴与地磁坐标系x(y)轴夹角为α(α一般较小，传感器安装放置时会尽量使α较小)，可以先测量地磁场水平分量(BDx,BDy)，从而得到夹角α=arctan(BDy/BDx)。

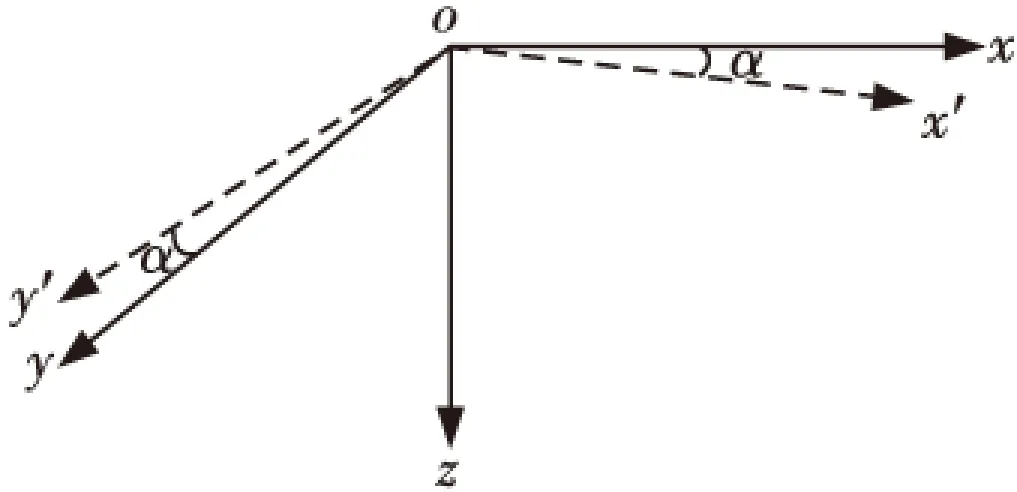
图2 传感器垂直时的坐标轴夹角Fig.2 The sensor coordinate axis' included angle with vertical direction

得到α角后，即可将传感器坐标系中的目标磁场值(Bx′,By′)通过转换矩阵变换到地磁坐标系中得到(Bx,By)，其变换关系为：

(2)

2 传感器倾斜放置的磁场测量

传感器倾斜放置的一般情况是：传感器的三个轴(x′,y′,z′)与地磁坐标系的三个轴(x,y,z)出现夹角，呈现不规则姿态(主要是z轴变得不垂直)，如图3所示，传感器放好后，两坐标系的轴夹角一般较小。传感器倾斜放置时所测得的目标磁场分量值与目标磁场在地磁坐标系中的磁场分量值存在差异，必须经过转换，才能得到需要的地磁坐标系中的目标磁场三分量值。

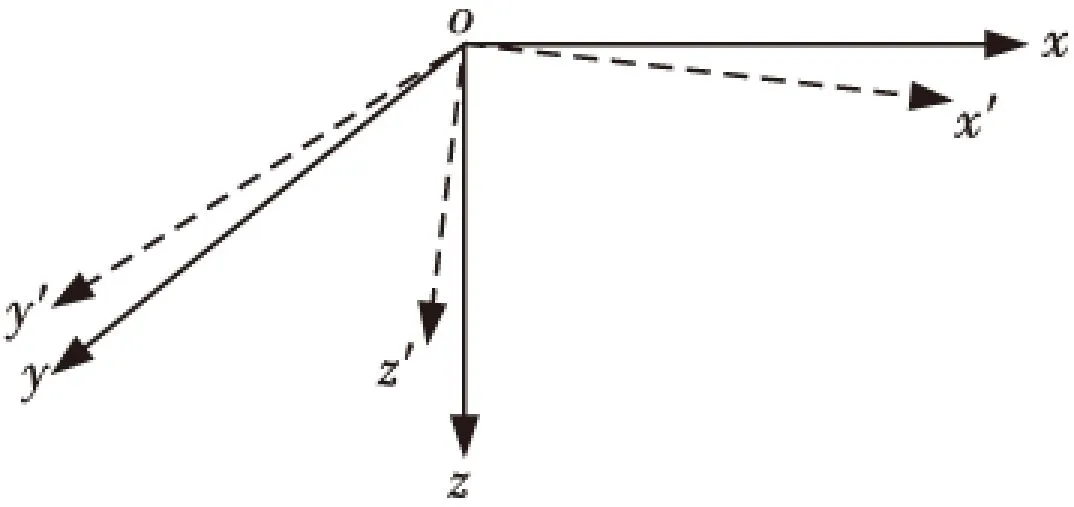
图3 传感器倾斜时的坐标轴Fig.3 The sensor's coordinate axis with slope direction

2.1 倾斜状态的转换矩阵

传感器的倾斜状态可以等效看作是传感器从理想放置状态绕z，x，y轴依次旋转α，β，γ角所呈现的姿态，用α，β，γ代表倾斜传感器的姿态角(文献[9]用姿态角的概念解决过舰船磁模型的分析问题)，以右手螺旋方向为姿态角正向，建立传感器的磁场测量转换矩阵。

经推导，倾斜状态下目标磁场测量值转换到地磁坐标系中的转换矩阵为：

(3)

转换矩阵求解关键是姿态角α，β，γ的求解。

2.2 传感器姿态角的求解

传感器倾斜时，已知地磁背景场(BD)的三分量测量值为地磁场在传感器三个轴的投影，如图4所示，传感器坐标轴绕地磁场向量旋转时，都能保证地磁场在传感器三个轴的投影不变，满足地磁场三分量测量值的传感器姿态有无数个，因此仅利用地磁场求不出传感器姿态角的唯一解，必须引入一个已知的辅助磁场，形成第二个已知背景磁场(B2)，两个已知的相交磁场向量即可确定唯一的传感器姿态。

在地磁坐标系中，地磁场(BD)和第二背景磁场分别记为B1(B1x,B1y,B1z)和B2(B2x,B2y,B2z)，传感器在理想状态时两个背景磁场的测量值则等于B1和B2。在实际中，传感器安装好以后难以再调整，因而无法确保实际测量得到理想的B1和B2，一般令B1直接取当地地磁场的真实值(BD)，第二背景磁场测量值B2由B2=B1+BF计算得到，其中BF为辅助磁场，是可以准确计算的外加磁场。BF不需要很大，可以由传感器(M)附近的通电线圈L产生(如图5所示)。两个背景磁场在传感器倾斜放置时的测量值记为B1′(B1x′,B1y′,B1z′)和B2′(B2x′,B2y′,B2z′)，求解姿态角时，B1′和B2′均取传感器的实际测量值。

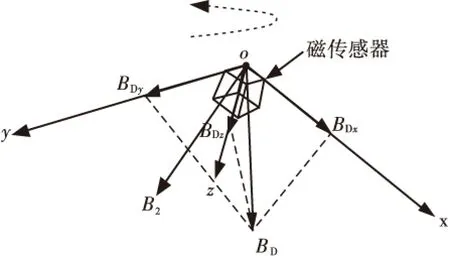
图4 传感器绕地磁场向量旋转Fig.4 The sensor's circumrotation surrounding the geomagnetic field

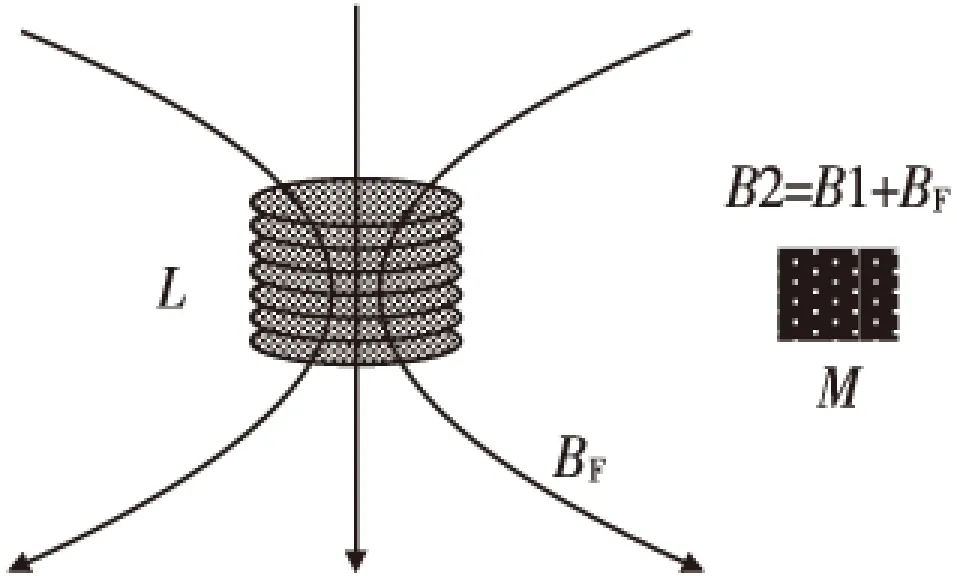
图5 第二背景磁场形成示意图Fig.5 The second background field's forming sketch map

为确定传感器的三个等效姿态角，利用已知地磁场和第二背景磁场在传感器理想放置和倾斜放置两个状态中的测量值，建立如下目标函数：

(4)

上述目标函数的优化采用寻优能力强、收敛速度快的微粒群优化(PSO)算法[10]。

3 实验验证

3.1 实验设计

实验中以地磁坐标系为基准坐标系。

随机抽取实验室中的两个三分量磁传感器1#和2#作为实验对象。由于实验室磁传感器近期没有进行校正的原因，不同传感器对同一地磁场的测量值会有一定的差异(实际中使用的传感器需要进行严格的测量参数校正，差异很小)，因此需要测量标准姿态时地磁场的三分量值，对两个传感器分别采取如下实验步骤：

1)将传感器调至标准姿态(理想放置状态)，记录传感器标准姿态时的地磁场读数，并计算传感器标准姿态时加入已知辅助磁场后的第二背景磁场值。

2)在传感器标准姿态下测量磁性目标的磁场(测量的真实值)。

3)将磁传感器倾斜放置(倾斜一定的角度)，记录地磁场的读数，加入同样的辅助磁场后记录传感器对背景磁场2的读数。

4)在传感器倾斜状态下测量同样磁性目标同样位置的磁场(记为测量值)。

5)根据式(4)用PSO算法求解传感器倾斜放置时的姿态角，由式(1)和式(3)对传感器倾斜放置时的目标磁场测量值进行转换，然后对磁场转换值和标准姿态下目标磁场的测量值进行比较分析。

由于篇幅限制，文中仅给出1#传感器的有关数据和结果。在本实验中，地磁场、辅助磁场和第二背景磁场在地磁坐标系中的值如表1所示，这也是传感器标准姿态时对两个背景磁场的测量值。在加入同样辅助磁场的情况下，1#传感器倾斜放置时对两个背景磁场的实际测量值如表2所示。

表1 标准姿态下1#传感器的背景磁场值

表2 倾斜放置时1#传感器的背景磁场测量值

实验中，1#传感器的磁场测试样本为某磁性目标的23个测量点的三分量磁场。

3.2 实验结果分析

对1#磁传感器，利用两个背景磁场在传感器两种姿态下的磁场值按照式(4)进行优化计算，求出的姿态角(α,β,γ)分别为7.045°，-4.238°和-3.451°，代入式(3)、式(1)对倾斜放置时的测量值进行转换(记为修正值)，并与测量值和真实值比较，迭代优化过程和比较结果如图6所示。

(a)目标函数变化 (b)x分量比较

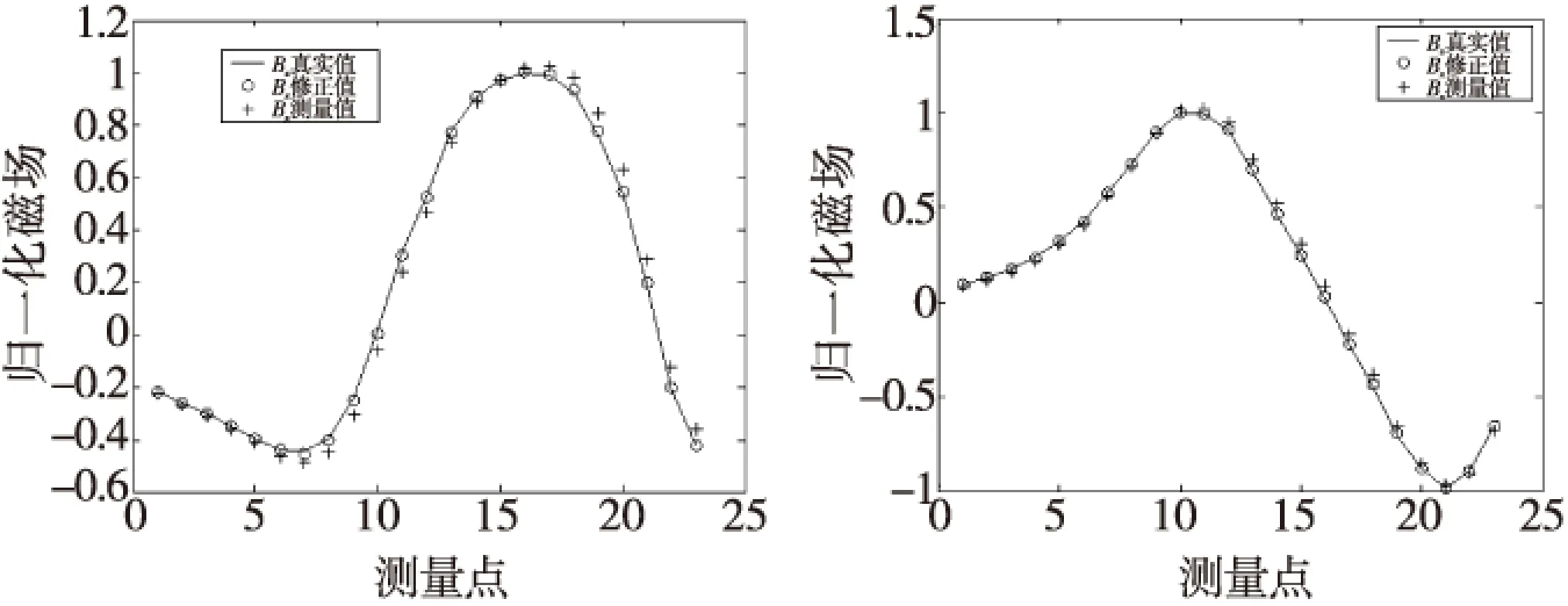
(c)y分量比较 (d)z分量比较图6 1#传感器实验结果Fig.6 The experiment result for 1# sensor

从图6的结果可以看出，采用PSO优化算法能够较快地收敛到姿态角的最优解，经过转换矩阵修正的磁场值非常接近磁场测量的真实值，比传感器倾斜放置时的测量值要好得多。磁场三分量测量值与真实值间的均方根误差为23.87%，5.54%，3.68%；磁场三分量修正值与真实值间的均方根误差为1.73%，0.74%，0.5%。可以看出，经过转换矩阵修正的磁场三分量值与真实三分量值间的均方根误差很小，最大1.73%(x分量测量值的修正误差)，与倾斜放置时的测量值相比，准确度有很大提高，可以代替磁场三分量的真实测量值。2#传感器也具有相似的结果，其最大误差为3.44%。

实验结果中，图6(b)中x分量的测量误差较大，主要是由于α角较大所致(x轴偏离较大)。结果中修正值和真实测量值存在一定误差，主要来源是：1)在计算辅助磁场时，由于传感器和辅助磁源的距离误差会带来第二背景磁场的计算误差；2)磁传感器本身的固有误差；3)在传感器标准姿态和倾斜姿态时，对磁性目标磁场重复测量时在同一测量点上存在位置误差。

4 结论

本文提出了三分量磁传感器倾斜放置时的磁场测量方法,该方法采用三个等效姿态角α、β、γ表示传感器的倾斜姿态，建立转换矩阵对磁场测量值进行修正。在仅利用地磁场无法唯一确定姿态角的情况下，引入已知辅助磁场，形成第二背景磁场，通过PSO算法求出传感器的姿态角，然后利用转换矩阵对目标磁场三分量测量值进行修正。实验结果表明，传感器倾斜放置时目标磁场的测量值经该方法修正后的值接近目标磁场的真实测量值，能够满足实际工程应用的需要。在一般的实验室磁场测量和工程应用中，有时难以保证传感器理想放置，这时都可以采用此方法进行处理，例如对于安装固定磁探头的消磁站，即可利用敷设好的线圈产生辅助磁场，利用本文方法对放置不理想的磁探头测量值进行修正，提高磁场测量精度。

[1]刘大明．舰船消磁理论与方法[M]．武汉：海军工程大学，2012．

[2]常宝林，渐开旺，张松勇．基于磁强计的消磁电流控制仪研制[J]．上海海事大学学报，2012，33(2)：22-25．

[3]JOHNJHOLMES．ApplicationofModelsintheDesignofUnderwaterElectromagneticSignatureReductionSystems[J]．NavalEngineersJournal, 2007 (4): 19-29．

[4]高金耀，翟国君，刘强．减弱船磁效应对海洋地磁测量精度影响的方法研究[J]．海洋测绘，2008，28(3)：1-5．

[5]李华，李庆民，龚沈光．基于磁性目标磁场模型的在线磁定位研究[J]．武汉理工大学学报，2009，33(1)：165-168．

[6]肖昌汉，何华辉．三分量磁传感器非理想放置时磁场数据的分析方法[J]．海军工程大学学报，1996，76(3)：7-11．

[7]KiskI,SandorPuszta.Applicationofmagneticfieldderivativesforlocatingsarmatiangraves[J]．JournalofAppliedGeophysics，2006，60(1): 13-26．

[8]曲晓慧，杨日杰，单志超．潜艇磁场建模方法的分析与比较[J]．舰船科学技术，2011，33(3)：7-11．

[9]李华，李庆民，刘君．两种舰船磁场模型结构的比较研究[J]．探测与控制学报，2007，29(S)：62-66．

[10]雷秀娟．群智能优化算法及其应用[M]．北京：科学出版社，2012．

Magnetic Field Measuring Method for Slantly Placed 3-components Sensors

ZHANG Zhaoyang1, YI Jun1, YU Weiqiao2

(1. Navy Equipment Technology Institute, Shanghai 200083, China; 2. Unit 91656 of PLA, Shanghai 200080, China)

To solve the problem that when the 3-axial magnetometer was slantly fixed, which could cause big error. A magnetic field measuring method was proposed. The method used 3 equivalent pose angles (α, β and γ) to represent the sensor’s sloping pose and founded a transform matrix to correct the measured value of the magnetic field. As the unique solution of the pose angles could not be gotten only by the local geomagnetic field, a known accessorial magnetic field was added to form the second background field. Then the pose angles could be calculated by PSO algorithm, and the measured value of the objective field could be corrected by the transform matrix. The experiment results of the 2 randomly chosen sensors showed that the value of the slantly placed sensor corrected by this method was close to the actual value of the objective field, and it could satisfy the demands of practical engineering.

3-axial magnetometer sensor; magnetic field correction; PSO algorithm; pose angle; transform matrix

2016-11-27

张朝阳(1981—)， 男，河北衡水人，博士，工程师，研究方向：舰船消磁分析研究。E-mail:zzy810514@163.com。

P631

A

1008-1194(2017)02-0072-04