基于Hopfield模型改进射线描迹的对流层延迟估计
陈西宏,吴文溢,2,童宁宁,李成龙,刘 赞
(1.空军工程大学防空反导学院,陕西 西安710051;2.西北核技术研究所,陕西 西安 710024)
基于Hopfield模型改进射线描迹的对流层延迟估计
陈西宏1,吴文溢1,2,童宁宁1,李成龙1,刘 赞1
(1.空军工程大学防空反导学院,陕西 西安710051;2.西北核技术研究所,陕西 西安 710024)
针对射线描迹法在估计对流层延迟方面受限于探空观测的问题,提出利用Hopfield模型改进射线描迹的对流层延迟估计方法。该方法利用Hopfield模型中的干、湿折射率计算公式,建立对流层大气折射指数剖面模型,并将其应用到射线描迹法改进中,克服探空观测的限制,扩大了射线描迹法的适用范围。选取国际GPS服务组织(IGS)中四个测站的气象数据,分别采用改进射线描迹模型和基于Neil映射函数(NMF)的Hopfield模型、Saastamoinen模型进行对流层延迟估计,计算结果表明,改进射线描迹模型的估计精度优于其他两种模型,为对流层延迟实时监测应用提供了新的方法。
对流层斜延迟;射线描迹法;Hopfield;折射指数
0 引言
对流层延迟[1-6]是GNSS(Global Navigation Satellite System)导航定位的主要误差源之一。对流层延迟量在天顶方向约为2 m,而随着高度角的降低延迟值将增大至20 m[7]。由于中性大气层是非色散介质,为了修正无线电信号传播路线上的延迟,通常需要先借助天顶延迟模型计算对流层天顶方向延迟,再通过映射函数投影到高度角方向。目前国际上常用的模型有Hopfield模型[8]、Saastamoinen模型[9]以及Neil映射函数(Neil Mapping Function, NMF)[10]等,其中天顶模型改正精度可以达到厘米级,但此类传统对流层延迟模型在估计对流层延迟方面仍存在局限性,比如传统天顶延迟模型多依赖测站的地表参数,其精度最终受到初始参数的限制,NMF映射函数某些参数需要实时更新,尤其估计低角度对流层延迟能力不足。
射线描迹法[11-12]通过估计无线电信号在大气传播的轨迹,能实现高精度的电磁波延迟修正。然而,描迹法中折射率剖面的计算同样需要探空气象数据的获取,这对于一些缺乏观测资料的地区存在一定的局限性。本文针对此问题,提出了基于Hopfield模型改进射线描迹的对流层延迟估计方法。
1 基于探空数据的射线描迹法
目前,探空技术是探测对流层大气的常用手段,也是获取对流层延迟的常用方法之一,基于探空数据获取的对流层斜延迟可以视为真值。射线描迹法是假设对流层大气球面分层,基于Snell定律给出的高精度电磁波延迟修正方法。通过探空观测获取大气折射率剖面后,利用射线描迹法可获得任意高度角的对流层延迟。电波射线描迹示意图如图1所示。
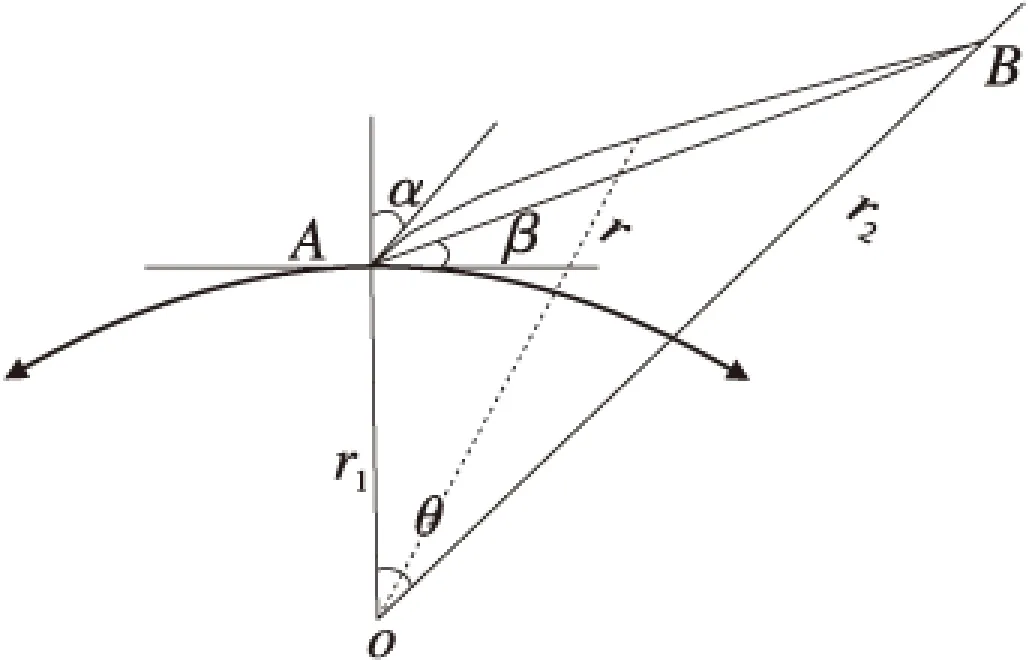
图1 射线描迹法示意图Fig.1 Schema of ray tracing
图1中,β为实际仰角,α为视在天顶角,r为此时电磁波上任一点和地心的距离,r1为地球半径,r2为目标到地心的距离,θ为圆心角。射线描迹法计算公式可表示为:
(1)
式(1)中,ΔS为电磁波在对流层中的传播延迟,n(r)为与地心距离r处的大气折射率,一般通过探空观测获取。利用射线描迹法计算对流层延迟通常基于探空观测,而探空观测存在一定的局限性,如测站分布过稀,观测间隔时间过长,在海洋和山区上空基本没有观测资料,且观测成本也在不断增加,因此,必须研究一种不依赖于探空数据的对流层延迟计算方案。
2 基于Hopfield改进射线描迹的对流层延迟模型
下面给出一种基于Hopfield模型折射率剖面计算方案。对流层大气折射率可由各层的气象参数计算得到,具体公式(Thayer,1974)如下:
(2)
式(2)中,N为总折射率,Nw为湿折射率,Nd为干折射率,P为大气压(mbar),e为水汽压(mbar),T为温度(K),k1=77.604 K/Pa,k2=64.79 K/Pa,k3=377 600 K2/Pa。
Hopfield模型认为对流层大气折射率可分为干、湿折射率,且随海拔高度的变化呈现一定的函数关系,在天顶方向上具体表现为:
(3)
(4)
式(3)、式(4)中,Nd0、Nw0分别为测站处的干、湿折射率,可通过测站的气象参数利用式(2)获取;hd、hw分别为对流层干、湿大气层顶高度(m),Hopfield模型中hd、hw可表示为:
hd=148.72(T0-273.16)+40 136
(5)
hw=11 000
(6)
式(5)中,T0为测站处温度。结合射线描迹法中折射指数公式,令:
r=h+r1
(7)
式(7)中,r为地心距,h为海拔高度,r1为地球半径。再将式(7)代入式(8)中得射线上任意一点折射指数为:
(8)
通过式(2)-式(8)可获取测站的折射率剖面,再代入式(1)中,即可对任意测站快速精确的估算不同仰角的对流层延迟。
3 算例与结果分析
选择四个日本地区代表性IGS站点2012年的气象和探空数据进行对流层延迟分析。以基于探空数据计算获取的对流层斜延迟结果作为参考值(真值),比较分析改进射线描迹法的可靠性和精度。所选测站的信息如表1所示。
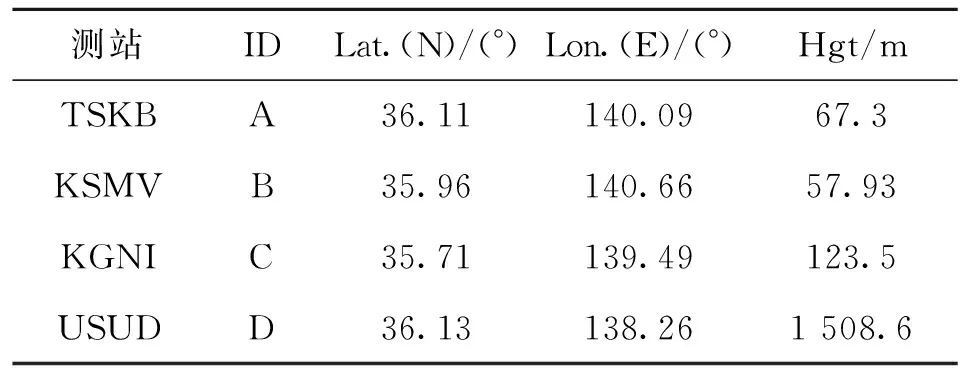
表1 测站情况表
表1中,“ID”为测站的代号,“Lat.”为测站纬度(Latitude),“Lon.”为测站经度(Longitude),“Hgt.”为测站海拔高度(Height)。
为了更好地验证本文所提改进模型的精度,采用以下两个方案进行对比分析。方案一:利用改进射线描迹法分别估计在仰角βi=90°,50°,30°,20°(i=1,2,3,4)共计4个高度角方向测站的对流层斜延迟;方案二:利用NMF映射函数,将由对流层天顶延迟模型Hopfield模型和Saastamoinen模型解算的对流层天顶延迟投影到上述的4个高度角方向获取四个测站的对流层延迟值,分别记为Hop-NMF模型和Saas-NMF模型。然后,将两种方案的结果与真值进行比较,采用偏差均值和RMS模型精度的验证标准。
表2和表3分别表示四个测站采用三种方法在4个高度角方向的对流层延迟偏差均值和RMS计算结果。为便于比较,将偏差均值和均取为绝对值。从表中可以看出,由于各站点周围对流层大气的温度、气压、湿度等在时间和空间上变化的复杂性和随机性,全年内不同测站点的对流层延迟估计精度差别较大,不论采用哪种模型,其中,KGNI站和USUD站的估计精度要高于TSKB站和KSMV站,偏差均值最大可达6.5 mm;Hop-NMF模型和Saas-NMF模型的精度相差不大,改进射线描迹模型的估计精度则要优于方案一中的两种模型,且随着高度角的降低,优势更加明显。

表2 三种模型对流层斜延迟偏差均值统计结果 (单位:mm)

表3 三种模型对流层斜延迟RMS统计结果 (单位:mm)
为了进一步验证模型的准确性和适用性,计算比较了各站在20°高度角下全年12个月份的偏差均值以及全月的偏差波动。以KGNI站和USUD站为例,图2显示了两站一年内各个月份的偏差均值波动情况,图3则给出了两站在九月份全月的偏差波动。比较结果可以得出以下结论:
1)从图2中可以看出,Hop-NMF模型和Saas-NMF模型全年12个月份的偏差均值波动趋势大致相当,两种模型在KGNI站和USUD站均出现了较大的系统性偏差,且呈现明显的季节性分布。其中,在KGNI站中,7月,8月,9月份的偏差均值较大,1月,2月,12月份的偏差均值较小;在USUD站中,6月,7月,8月份的偏差均值较大,11月,12月,1月份的偏差均值较小。因此,总体上来说Hop-NMF模型和Saas-NMF模型的全年偏差大体呈现夏季偏大、冬季偏小的季节性分布。
2)改进射线描迹模型的全年偏差均值波动并没有出现明显的季节性分布,而是表现为在零值附近波动。相比于Hop-NMF模型和Saas-NMF模型,改进模型在某些月份的偏差均值与这两种模型相当,而在7月,8月,9月等夏季时节的月份则要明显优于Hop-NMF模型和Saas-NMF模型。
3)从图3中9月份的偏差波动情况可以看出,Hop-NMF模型和Saas-NMF模型的偏差抖动情况较为剧烈,相邻天的误差最大可以达到8 mm;改进模型的偏差波动则较为平缓,相邻天的误差不超过4 mm。
4)基于映射函数(NMF)的对流层延迟模型操作简单、适用性强,但系统偏差抖动较大,且呈现明显的季节性偏差。改进模型考虑到大气的折射率随高度的变化,对每层大气的折射率进行连续积分,不仅克服了探空数据的限制,且估计精度和稳定度比映射函数模型要好。

图2 KGNI站和USUD站12个月份偏差均值Fig.2 Bias on KGNI and USUD stations in months

图3 KGNI站和USUD站九月份偏差波动情况Fig.3 Bias on KGNI and USUD stations in ninth month
4 结论
本文提出了基于Hopfield模型改进射线描迹的对流层延迟估计方法,该方法利用Hopfield模型中的干、湿折射率计算公式,建立对流层大气折射指数剖面模型,并将其应用到射线描迹法改进中,克服探空观测的限制。通过对IGS测站气象数据的计算和分析,结果表明,改进射线描迹模型精度优于传统对流层延迟模型,验证了此方法的可靠性和可行性。另外,此方法能在缺少探空数据的情况下,较精确地估计出对流层斜延迟,不但可应用于GPS系统,而且也适用于我国的北斗二代卫星导航系统,对于我国卫星导航系统的对流层延迟监测应用具有一定的参考意义。
[1]赵静旸, 宋淑丽, 陈钦明, 等.基于垂直剖面函数式的全球对流层天顶延迟模型的建立[J].地球物理学报,2014,57(10):3140-3153.
[2]黄良珂, 刘立龙, 文鸿雁, 等.亚洲地区EGNOS天顶对流层延迟模型单站修正与精度分析[J].测绘学报, 2014,43(8):807-817.
[3]毛健, 朱长青, 郭继发.一种新的全球对流层天顶延迟模型[J].武汉大学学报(信息科学版), 2013,38 (6):684-688.
[4]张利军,张蕊,赵振维.对流层散射传播中的偏移损耗分析[J].电子与信息学报, 2015, 37(6):1502-1506.
[5]CHEN Xihong, LIU Qiang, HU Denghua, et al.Delay analysis of two way time transfer based on troposphere gradients[C]// The 10th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM 2014).Beijing China, 2014: 543-547.
[6]吴文溢,陈西宏,孙际哲,等.改进的对流层天顶延迟估计方法[J].探测与控制学报,2016,38(5):96-100.
[7]David E, Macmillan D S, John M G.Tropospheric delay ray tracing applied in VLBI analysis[J].Journal of Geophysical Research: Solid Earth, 2014, 119(12): 9156-9170.
[8]Johannes B, Gregor M, Michael S, et al.Development of an improved empirical model for slant delays in the troposphere (GPT2w)[J].GPS Solutions, 2015, 19(3): 433-441.
[9]姚宜斌, 张豹, 严凤, 等.两种精化的对流层延迟改正模型[J].地球物理学报, 2015, 58(5):1492-1501.
[10]ZHAO Jinyang, SONG Shuli , CHEN Qingming, et al.Establishment of a new global model for zenith troposphere delay based on functional expression for its vertical profile[J].Chinese Journal of Geophysics, 2014, 57(10):3140-3153.
[11]陈西宏, 刘赞, 刘继业, 等.低仰角下对流层散射斜延迟估计方法[J].电子与信息学报, 2016, 38(2):408-412.
[12]朱庆林, 吴振森, 赵振维,等.单台地基卫星导航接收机测量对流层斜延迟[J].电波科学学报,2010,25(1):37-41.
Tropospheric Slant Delay Estimation Based on Improved Ray Tracing of Hopfield Model
CHEN Xihong1, WU Wenyi1,2, TONG Ningning1, LI Chenglong1, LIU Zan1
(1.Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China;2.Northwest Institute of Nuclear Technology, Xi’an 710024, China)
The method of ray tracing on tropospheric slant delay estimation is restrained by air-sounding observation. An improved ray tracing method combined with Hopfield mode was proposed in this paper. This method established tropospheric refractivity profile model, which used dry/wet refractivity formula in Hopfield model. It was introduced into ray tracing method to relieve the dependence on air-sounding data, which helped to expand the field of application. Then, meteorological data of four observation station from International GPS Service (IGS) was selected, and tropospheric slant delay based on the improved ray tracing, Neil Mapping Function (NMF) based Hopfeild model and Saastamoinen model were respectively calculated. The results showed that the improved ray tracing method was prior than other two mode for estimating tropospheric slant delay in precise.
tropospheric slant delay; ray tracing; Hopfield; refractive index
2016-11-12
陈西宏(1961— ),男,陕西蓝田人,博士,教授,博士生导师,研究方向:防空反导武器系统信息技术。E-mail:xhchen0315217@163.com。
TN011
A
1008-1194(2017)02-0062-04
——环地平弧&环天顶弧

