基于软判决求解含错方程的自同步扰码盲识别
尹 瑾,王建新
(南京理工大学电子科学与光电技术学院,江苏 南京210094)
基于软判决求解含错方程的自同步扰码盲识别
尹 瑾,王建新
(南京理工大学电子科学与光电技术学院,江苏 南京210094)
针对低信噪比情况下自同步扰码的识别问题,提出了基于软判决求解含错方程的自同步扰码盲识别方法。该方法首先通过硬判决序列识别出扰码多项式的阶数,建立含错方程组;然后提取软判决序列中比特的可靠度信息,根据选取的解向量将可靠度转化为每个方程成立的概率,找到使方程组成立概率最大的解向量,即为真正的扰码多项式。仿真实验表明,相比于基于硬判决的沃尔什-哈达玛变换(Walsh-Hadamard Transformation, WHT)算法,该方法在低信噪比下的容错性能较好。
自同步扰码;盲识别;软判决;含错方程
0 引言
在实际通信中,为了提高数据传输的准确性和抗干扰能力,信号在传输前常采用扰乱编码技术。扰码识别对扰码的编码参数进行逆向分析,在信号截获等领域有着重要意义。自同步扰码因其保密性强且不需要收发双方的严格同步而广泛应用于通信系统中,本文主要研究自同步扰码的盲识别问题。
文献[1]利用 BM算法求解关键方程来求得生成多项式,但算法的不容错限制了可用性;文献[2]根据扰码序列的特征,利用Walsh-Hadamard变换法解含错方程组来识别自同步扰码的生成多项式;文献[3]是基于信源的0,1不平衡性,通过计算扰码序列与原始扰码序列的相关度来判断扰码多项式;文献[4]提出基于重码统计的自同步扰码多项式阶数的盲测定方法,但该阶数识别方法需要很大的搜索量;文献[5]是以比特状态统计的概率分布与均匀分布的修正平方欧几里德距离作为比特状态不平衡性的衡量标准,来实现自同步扰码的识别。文献[6]分析了信源0,1 分布不平衡下的自同步扰码的游程统计规律,为扰码多项式阶数的判定提供了一种有效方案。文献[7]提供了一种线性分组码的自同步扰码识别方法。
以上的算法均是建立在解调硬判决序列的基础上,由于接收端的软判决序列中不仅含有比特符号信息,还含有比特的可靠度信息,硬判决算法相当于丢弃了其中的可靠度信息,在低信噪比下识别的容错能力较差。本文针对此问题,提出基于软判决求解含错方程的自同步扰码盲识别方法。
1 自同步扰码盲识别基础
自同步扰码器主要由线性反馈移位寄存器(Linear Feedback Shift Register,LFSR)构成。信息xk经过加扰输出zk的过程如下:
(1)
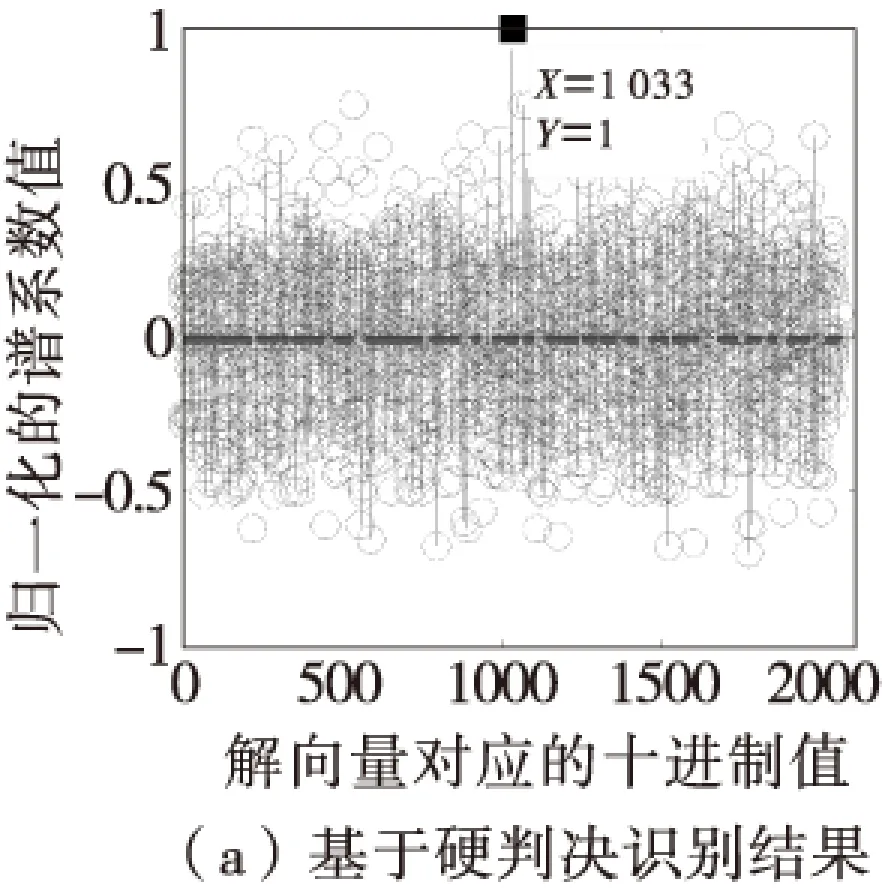
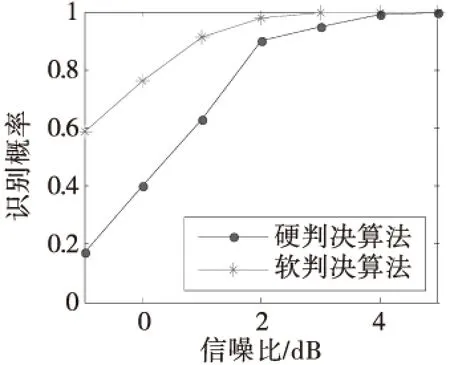
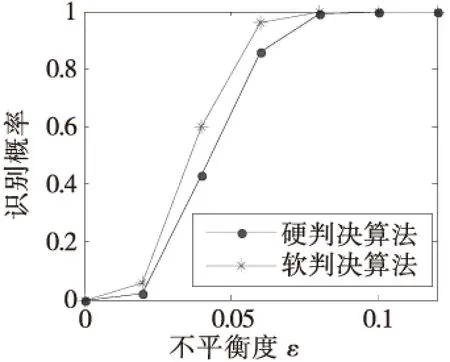
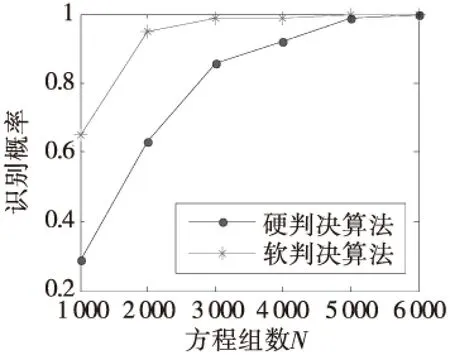
其中,ci∈GF(2)为LFSR的反馈系数,0 自同步扰码盲识别的任务是识别解码所需要的扰码多项式级数和扰码多项式。 1.1 扰码多项式阶数识别 根据m序列的统计特性[8],一个周期内,n级m序列同一游程长度的游程个数按1/2的规律递减,递减规律在长为n-1的1游程和长为n的0游程处发生变化,这个变化点即为生成m序列的最小多项式的级数n。 在信源0,1分布不平衡度为ε的条件下,自同步扰码输出与m序列有1/2+ε的符合优势。通过对接收硬判决序列进行游程统计,找出游程的个数1/2递减规律的变化点,即可估计出扰码生成多项式的阶数[8]。 1.2 含错方程组模型 根据式(1)中的自同步扰码LFSR的反馈系数ci,相应的扰码多项式可以表示为: f(x)=1+c1x1+c2x2+…+cLxL (2) 设扰码器的输出为a=(a0,a1,a2,…),当输入扰码器的信息为0时,有如下递推关系: (3) 根据式(3),对于长为Ns的自同步扰码序列,经过变换后可以得到如下的齐次方程组在二元域GF(2)上成立[8]: (4) 当输入扰码器的信息为0时,有: (5) 此时方程组(4)中对应的方程不成立而变为含错方程组。 将自同步扰码器输出序列中与齐次方程的行向量对应的一组比特定义为自同步扰码的一个码字ai,则其码长nl=L+1,ai=(ai,1,ai,2,…,ai,L+1)=(ai,ai+1…,ai+L)。对应ai的接收端硬判决码字记为αi=(αi,1,αi,2,…,αi,L+1),记接收硬判决的码字矩阵为Ah,扰码多项式系数向量为c,可以建立如下的含错方程组模型: Ah·c=0 (6) 1.3 基于硬判决的WHT识别法 (7) 2.1 利用软判决序列的识别算法 基于硬判决的WHT识别法主要是从统计方程成立的个数出发求解含错方程组,系数矩阵Ah中的系数向量一旦出现误码比特即作为错误向量统计,低信噪比的情况下很可能找不到正确的解。利用接收软判决序列可以从方程成立概率的角度考虑含错方程组(6)的求解。 首先需要从软判决序列中获取每比特的可靠度信息。选取可能的解向量,根据解向量可以将比特的可靠度信息转化为方程系数向量的可靠度。根据n阶Hadamard矩阵本质上存储了所有n维向量相乘结果的思想,定义新的矩阵存储方程系数向量与解向量的相乘结果,依据相乘结果的不同,区分该方程系数向量的可靠度表征的是方程成立概率还是不成立概率,进而得到解向量使整个方程组成立概率大小的度量,实现对含错方程组的求解。 2.2 软判决序列中的可靠度获取 对自同步扰码器输出的扰码序列进行BPSK调制,通过AWGN信道模型,则扰码的码字ai中比特ai,j对应的接收软判决为: ri,j=(1-2ai,j)+ei,j (8) 其中,ei,j为加性白噪声,服从均值为0,方差为σ2的正态分布。则矩阵Ah中的硬判决比特由式(9)得到: (9) 在AWGN信道下,p(ri,j|ai,j)的概率密度函数[10]为: (10) 由于ai,j取值的后验概率可以表示为: (11) 在扰码序列0,1等概的条件下,P(ai,j=0)=P(ai,j=1)=0.5。同时根据p(ri,j)=p(ri,j|ai,j=0)P(ai,j=0)+p(ri,j|ai,j=1)P(ai,j=1),并将式(10)中的概率密度取值代入后验概率式(11),化简后得到后验概率表达式为: (12) (13) 软判决序列中包含每个比特的可靠度信息,当λ≥1,比特的硬判决结果为0时,P(ai,j=0|ri,j)的值越大该比特越可靠;当λ<1,比特的硬判决结果为1时,P(ai,j=1|ri,j)的值越大该比特越可靠。定义度量每个接收比特序列ai,j的可靠度为w(ai,j),根据式(13),用λ来表征得到: (14) 由接收软判决ri,j求得λ的值,代入式(14)即可得到该比特的可靠度w(ai,j)。 2.3 基于可靠度的含错方程组求解 下面从方程成立概率的角度出发,根据可靠度信息进行含错方程组的求解。 (15) 当向量长度较大时,计算复杂度必然迅速增加,因此在实际中并不适用。由于每个系数向量中可靠度最小的比特判决错误的概率最大,其他比特判决错误概率较低,因此整个向量的w(αi)主要由可靠度最小的有效比特的可靠度决定,有如下的近似关系[11]: (16) 定义结果矩阵H=Ah·ck,其元素h存储了方程系数向量αi与解向量ck在GF(2)域上的相乘结果。当h=αi·ck=0时,表示方程成立;当h=αi·ck=1时,表示方程不成立。根据式(14)和式(16),方程系数向量的可靠度w(αi)由后验概率表征,可以进一步得到方程成立的概率和不成立的概率。值得注意的是,对于h=1的情况,方程系数向量的可靠度w(αi)表征的是方程不成立的概率,方程成立的概率为1减去方程不成立的概率。则第i个方程成立的概率可以表示为: (17) 对于每个候选解向量ck,可以通过每个方程成立概率的乘积求得整个方程组成立的概率作为解向量的符合度量度。由于多个概率相乘的结果接近于0,可能会影响计算精度,引入似然比LRi作为方程成立可靠度的度量,其取值为第i个方程的成立概率和不成立概率之比,由式(17)易得LRi的取值可以表示如下: (18) 由于对数函数的单调递增特性不会影响解向量的正确选取,引入对数函数L(ck)作为解向量ck的符合度函数,表示解向量使方程组成立概率大小的量度,定义如下: (19) 在可能的解向量集合中求得使L(ck)最大的解向量即为Ah·c=0的最优解向量,即真正的扰码多项式。 2.4 基于软判决的识别算法步骤 发送扰码序列每比特ai,j对应的接收硬判决为αi,j,接收软判决为ri,j,1≤i≤N,1≤j≤L+1,N为方程个数,L为扰码多项式阶数,基于软判决的识别算法步骤如下: 1)将获取的硬判决结果放入矩阵Ah中,先由接收软判决ri,j求得每个比特的可靠度w(ai,j),再根据式(16)求得第i个方程系数向量的可靠度w(αi); 2)选取一个L+1维的二进制向量作为候选解向量ck,其中c0=cL=1; 3)计算结果矩阵H=Ah·ck,根据H对应位置的结果利用式(17)计算出每个方程成立的概率Pi,再根据式(18)和式(19)式计算得到方程组成立概率量度的对数函数L(ck); 4)重复步骤2)、3),遍历可能的解向量,找到使L(ck)取得最大值的解向量即为正确的解,扰码多项式识别结束。 本算法利用了软判决中的可靠度信息,在较低信噪比下,识别表现将优于基于硬判决的WHT识别法,且本文算法可以选取可能的解向量,减少了需要遍历的解向量数。 3.1 算法有效性仿真 为验证本文算法,使用Matlab进行仿真。取原始信息为0,1不平衡度ε=0.1的二进制序列,序列长度为20 Kb,自同步扰码器的生成多项式设为g(x)=1+x3+x10。对自同步扰码序列进行BPSK调制,信道模型为AWGN模型,信噪比设为SNR=1 dB。 首先估计扰码多项式的阶数L,表1中为对硬判决序列的游程统计结果。表中容易看出,k<9的游程数大致按1/2的递减规律分布,k=9的1游程数明显下降而0游程数多,k=10的0游程数很少,k>10的0,1游程数都很少,由这个明显的不平衡判断出扰码多项式的级数L=10。 表1 游程统计结果 根据扰码多项式级数建立方程组,由于识别概率与接收的数据量有关,将方程个数N作为所用数据量的度量。取方程数N=2 000,图1是基于硬判决的WHT识别法和软判决算法的仿真结果,纵坐标分别为归一化的谱系数值和归一化的方程组成立概率量度。 如图1所示,峰值的横坐标值均为1 033,化为二进制的结果向量为(10000001001),与扰码多项式的系数从高位到低位排列得到的向量形式一致,识别结果正确。在软判决算法仿真结果图中,正确解向量处的峰值更加突出,识别效果更好。且本文的软判决算法中,利用已知c的第一位和最后一位均为1来减少遍历的解向量个数,识别效率更高。 3.2 算法性能仿真和分析 取原始信息为0,1不平衡度ε=0.1的二进制序列,方程数N=2 000,在不同的信噪比下分别对硬判决WHT算法和软判决算法进行蒙特卡罗仿真实验,仿真次数为1 000次,得到扰码多项式的识别概率如图2所示。由仿真结果可以得到在信噪比大于1 dB时,两种算法的识别概率均能达到90%以上,且在较低信噪比下,本文的软判决算法识别概率明显高于硬判决算法。 由于信息的0,1不平衡度影响自同步扰码的识别结果,将AWGN模型信噪比设为SNR=5 dB,选取方程数N=2 000,在原始序列0,1不平衡度ε不同的情况下进行仿真,得到仿真结果如图3所示。从图中可以看出,随着不平衡度ε的增大,两种算法的识别概率均呈上升趋势,相同的不平衡度下软判决算法的识别率较好。 图4为将AWGN模型信噪比设为SNR=1 dB,不平衡度ε=0.1时,选取不同的数据量对算法进行实验得到的仿真结果。可以看出,随着数据量的增加,两种算法的识别概率均上升,方程数取N=2 000时,本文的识别算法即可达到90%以上的识别概率。由此得到,在相同的信道仿真条件下,为了达到相同的识别概率,软判决算法需要的数据量更少。 图2 不同的信噪比下识别结果Fig.2 The recognition results under different SNR 图3 不平衡度ε不同时的识别结果Fig.3 The recognition results under differentε 图4 不同数据量下的识别结果Fig.4 The recognition results under different N 本文提出了基于软判决求解含错方程的自同步扰码盲识别方法。该方法主要从方程组成立的概率角度出发,通过提取软判决序列中的可靠度信息,求解含错方程组,识别出自同步扰码的生成多项式。仿真实验表明,相比于基于硬判决的WHT算法,新方法在低信噪比下的容错性能较好。在需要达到相同的识别概率时,软判决算法可以节省所用数据量,在工程中有一定的应用价值。本文算法受信息0,1不平衡度影响较大,未来的研究应对算法进一步优化。 [1]MasseyJL.Shift-registersynthesisandBCHdecoding[J].IEEETransactiononInformationTheory, 1969,15(1):122-126. [2]杨忠立,刘玉君.自同步扰乱序列的综合算法研究[J].信息技术,2005(2):30-32. [3]张永光,王挺,楼才义.一种自同步扰码生成多项式的盲识别方法:中国,102201912A[P].2011-09-28. [4]吕喜在,苏绍璟,黄芝平.一种新的自同步扰码多项式盲恢复方法[J].兵工学报,2011,32(6):680-685. [5]廖红舒,袁叶,甘露.自同步扰码的盲识别方法[J].通信学报,2013,34(4):136-143. [6]黄芝平,周靖,苏绍璟,等.基于游程统计的自同步扰码多项式阶数估计[J].电子科技大学学报,2013,42(4):541-545. [7]吕全通,张旻,李歆昊,等.基于码重分布距离的自同步扰码识别方法[J].探测与控制学报,2015,37 (5):7-12. [8]张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010. [9]李胜华,曾祥勇,胡磊,等.基于两族函数的低相关二元序列集构造[J].电子学报,2007,35(11):2215-2219. [10]LinS,CostelloDJ.ErrorControlCoding(SecondEdition)[M].NewJersey,USA:PrenticeHall,2005. [11]HagenauerJ,OfferE,PapkeL.Iterativedecodingofbinaryblockandconvolutionalcodes[J].IEEETransactionsonInformationTheory,March1996,42(2):429-445. Self-synchronous Scrambler Blind Recognition Based on Soft-decision Solving Error-containing Equation YIN Jin,WANG Jianxin (School of electronic and optical engineering, Nanjing University of Science and Technology, Nanjing 210094, China) To solve the self-synchronized scrambler recognition problem in the case of low signal to noise ratio, a blind recognition method of self-synchronous scrambler through solving error-containing equation based on soft-decision was proposed. Firstly, the order of the scrambling polynomial was recognized according to the hard-decision sequence and the error-containing equation set was built. Then the bit reliability information was obtained from the soft-decision sequence and the probability of the establishment of each equation was calculated from the reliability according to the selected solution vector.The solution vector which made maximum probability of the establishment of the equation set was searched, which was the real scrambling polynomial.Simulation results showed that this method had a better fault tolerance at low signal to noise ratio compared to the Walsh-Hadamard Transformation method based on hard-decision. self-synchronized scrambler ; blind recognition; soft-decision; error-containing equation 2016-11-14 尹瑾(1991— ), 女,江苏徐州人,硕士研究生,研究方向:信道编码和扰码盲识别。E-mail:yinjin2014@126.com。 TN911.22 A 1008-1194(2017)02-0044-05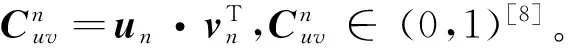

2 基于软判决求解含错方程的自同步扰码盲识别
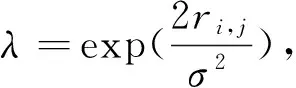
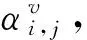
3 仿真实验和结果分析

4 结论

