基于Lyapunov优化的时变无线传感网路由研究*
董齐芬,张其前
(浙江警察学院计算机与信息技术系,杭州 310053)
基于Lyapunov优化的时变无线传感网路由研究*
董齐芬*,张其前
(浙江警察学院计算机与信息技术系,杭州 310053)
针对无线传感网应用中监测环境具有随机性和不可预测性等因素使得节点感知速率通常是时变的且某些时刻会超出链路容量的实际问题,设计了一种时变路由算法。在该算法中,将时变感知速率下的路由问题建立成以时均的网络能耗与丢弃感知数据代价的加权和最小为目标的随机优化模型,并利用Lyapunov优化技术求解该模型,进而得到一种路由策略来实时决策每条链路上的数据流量以及由于节点感知速率持续超出链路容量而不得不丢弃的数据量。进一步,讨论感知数据不被丢弃的条件,建立目标函数与感知信息最大传输时延之间的权衡关系。最后,通过仿真实验,验证了本文算法在能耗、感知数据的丢弃量及传输时延之间的均衡关系。还在不同的最大数据感知速率下,比较了本文算法与AVE算法的性能。
无线传感器网络;时变路由;Lyapunov优化
无线传感器网络WSNs(Wireless Sensor Networks)作为物联网的“末梢神经”,是一种综合信息采集、处理和传输功能于一体的新型网络信息系统,在环境监测、智慧城市、公共安全等领域有着广泛应用前景。但通常地,WSNs节点的能量、通信距离和链路容量等资源均是受限的。在满足链路容量等有限资源约束的前提下,如何设计能量有效的路由机制一直以来都是WSNs研究热点之一[1]。
目前,基于能量有效的路由研究已取得一定成果。其中,将最大化WSNs生存周期的路由问题直接建模或转换成线性规划模型并采用经典的最优化法或最短路径树、人工智能等方法求解的研究思路受到了学者们的青睐。文献[2]是较早用线性规划模型表示网络生存周期最优路由问题的典型代表作。该模型考虑了流量平衡约束和能耗约束,并采用次梯度算法实现分布式求解。在此基础上,不少学者进一步考虑实际条件,对这类问题深入研究[3-7]。如文献[3]考虑WSNs中有多个Sink节点的情况,并将多个Sink节点的数据收集路由问题分解成若干个单个Sink节点的路由问题,从而建立优化网络生存时间的路由模型;文献[4]在文献[2]模型的基础上增加了链路的带宽资源约束;针对节点的位置不平等造成节点能耗不均衡从而在一定程度上减低了网络生存时间的问题,文献[5-7]采用Sink节点移动的方法解决。他们在求解最优路由的同时优化Sink节点的移动路径或移动Sink节点在每个位置的停留时间。最近,还有学者研究如何根据节点剩余能量、节点度及邻居节点状态等参数来自适应调节路由以均衡节点能耗[8-9]。
上述成果为能量有效的路由机制提供有力的理论支撑,但大部分认为节点感知速率是常量。然而在实际应用中,由于监测环境具有随机性,节点感知速率通常是时变的。文献[10-12]虽然对时变感知速率问题进行了研究,但其前提是节点的平均感知速率是已知的。在具有随机性和不可预测性的监测环境中,节点的平均感知速率也是很难获取的。本文对此问题进一步深入研究,设计一种时变路由算法。该算法还考虑了节点感知速率超出WSNs链路容量时的特殊情况。主要贡献归纳为:①考虑WSNs应用中监测环境具有随机性和不可预测性等实际因素,将时变感知速率下的路由问题建立成以时均的网络能耗与丢弃感知数据代价的加权和最小为目标的随机优化模型;②利用解决无线网络中的队列系统动态控制问题的Lyapunov优化技术[13],设计一种时变路由算法;③讨论感知数据不被丢弃的条件,建立网络能耗与感知信息的最大传输时延之间的权衡关系;④通过仿真实验来验证本文提出的时变路由算法的可行性和有效性,并与基于平均感知速率的路由算法进行比较。
1 问题描述与建模
用G(V,L)表示一个无向连通的无线传感器网络,其中,V是所有节点的集合,包含N个传感节点和1个Sink节点,L是所有无线链路的集合。设Pmax为允许的节点最大发射功率,如果节点i和节点j之间进行无线通信所需的发射功率小于Pmax,那么称节点i流向节点j的无线链路lij∈V存在,且无线链路是双向存在的(但Sink节点没有出链路),节点i和节点j相互称为邻居节点。令Ni表示节点i的所有邻居节点的集合。为方便叙述与分析,再作如下定义与假设:
①传感节点同时承担数据采集和中继任务。
②传感节点的能耗主要用于收发数据,忽略数据感知、计算等能耗。

式中:dij表示节点i与节点j之间的距离,Eelec代表收发单位比特数据时的电路电子能耗,εfs是放大单位比特数据时所需要的电子能耗。
④无线链路的带宽资源是有限的,设单位时间内每条链路上的最大数据传输量为Rmax。
⑤由于WSNs应用中的监测环境具有随机性和不可预测性,故不同节点在单位时间内的数据感知量均不同且是随机的。令节点i在时间t的数据感知量为ai(t),且有amin≤ai(t)≤amax,其中的amin和amax分别表示节点在单位时间内的最小和最大数据感知量。
由于传感节点的数据感知速率随机可变,且无线链路的带宽资源受限,故无法保证当前时间内的所有感知数据都能发送到Sink节点。为了利用带宽资源受限的无线链路将感知信息在允许的收集时延要求内传输到Sink节点,本文首先将每个节点的感知数据存储在相应队列中,然后通过一定的策略进行处理。具体地,令Qi(t)为节点i的感知数据存储队列在时间t的存储量,且根据下式更新:
Qi(t+1)=max{Qi(t)-ρi(t)-bi(t),0}+ai(t), ∀i,t
(1)
式中:Qi(0)=0;ρi(t)≥0和bi(t)≥0是需要决策的变量,其中:ρi(t)表示在时间t发送出去的关于节点i的感知数据量。为使得当前发送出去的数据能被Sink节点接收到,每个传感节点应满足数据流量平衡约束:
(2)
式中:γij(t)≥0表示在时间t节点i发送给其邻居节点j的数据量。因为单位时间内每条链路上的最大数据传输量是有限的,所以γij(t)应满足如下约束:
γij(t)+γji(t)≤Rmax,∀lij∈L且j≠Sinkk节点
γij(t)≤Rmax,j=Sink节点
(3)
bi(t)表示当出现传感节点的感知速率持续超出链路容量的特殊情况时不得不丢弃的数据量。用单调递增的凸函数c(x)=α(x2+x)来表征丢弃感知数据的代价,其中α是可调系数。该代价函数表明当α给定时,丢弃的感知数据越多,对整个应用系统的影响越大,且随着丢弃数据量的增加,其影响更是急剧增大的。为防止丢弃过多数据量从而破坏系统性能,令单位时间内允许节点丢弃的最大数据量为bmax。
根据Lyapunov优化技术,为确保感知信息的收集时延是有限的,每个队列应是可稳定的,即:
(4)
式中:E{·}表示数学期望。
随着无线充电技术和智能移动节点的发展,可在WSNs中部署移动充电站为传感节点提供高效及时的充电服务,以保证传感节点持久正常地工作[14-15]。但是,这并不代表可以任意浪费节点能量,因此减少网络能耗从而降低充电代价仍是WSNs研究中的重要指标。故本文目标是在满足上述各项约束的前提下,合理决策ρi(t)、γij(t)及bi(t),使时均的网络能耗与丢弃感知数据代价的加权和最小,即建立如下的随机优化模型:
(5)
2 算法设计
可以采用动态规划或马尔科夫决策求解上述随机优化模型,但前提是节点感知数据量的先验统计信息是完全可知的。然而,对事件发生具有不可预测性的WSNs应用来说,这很难满足。为此,本节引入解决无线网络中的队列系统动态控制问题的Lyapunov优化技术,设计一种可行有效的算法求解上述随机优化模型,使得在任意时间t,只要根据当前观测值,即可计算出ρi(t)、γij(t)及bi(t)。
2.1 预备知识
定义虚拟队列:
Zi(t+1)=
max[Zi(t)-bi(t)-ρi(t)+δ1{Qi(t)>0},0], ∀i,t
(6)
式中:Zi(0)=0;δ是可调参数,其取值影响感知数据的收集时延和随机优化问题(5)的目标函数值;1{Qi(t)>0}是符号函数,当Qi(t)>0时,它为1,否则为0。首先,给出与感知信息传输时延有关的引理[13]。
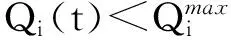
(7)
再记Θ(t)=[{Qi},{Zi}]为当前感知数据存储队列和相应虚拟队列的向量,并定义二次型Lyapunov函数:
(8)
根据感知数据存储队列和相应虚拟队列的更新式(1)和(6),有:
(9)
最后一个不等式由0≤bi(t)≤bmax得到。然后,定义一阶Lyapunov平移函数Δ(Θ(t)):
Δ(Θ(t))=E{L(Θ(t+1))-L(Θ(t))|Θ(t)}
(10)
进一步,将随机优化问题(5)的目标函数以惩罚项的形式与Lyapunov平移函数相加,得到以下的Lyapunov平移函数-加-惩罚函数:
(11)
式中:V是可调参数,其取值也会影响数据收集时延和随机优化问题(5)的目标函数值。由式(9)可得:
(12)
2.2 算法实现
给出基于Lyapunov优化的WSNs时变路由算法,如表1所示。算法的实现遵循Lyapunov优化技术的基本思路,即选择一种策略ρi(t)、γij(t)及bi(t),使得式(12)不等号右边的表达式最小。

表1 基于Lyapunov优化的WSNs时变路由流程
2.3 算法性能分析
分析当感知数据量ai(t),∀i服从独立同分布时本文算法的性能。
定理1 若参数δ满足0<δ≤E{ai(t)},∀i,且bmax≥amax,那么,提出的算法具有以下特性:
①在任意时间t内,节点i的感知数据存储队列及相应的虚拟队列均满足:
Qi(t)+Zi(t)≤Ωmax, ∀i
(15)
式中:Ωmax=Vα+2bmax(Vα+1)+amax。
②感知数据的最大收集延时为:
(16)
③对∀t,若节点i均有Qi(t)+Zi(t)≤Vα-δ时,则节点i的感知数据不会被丢弃。
④令ρi(t)、γij(t)及bi(t)是根据算法1计算的值,φ是相应的时均网络能耗和丢弃感知数据代价的加权和。那么,φ与随机优化问题(5)的最优目标函数值φopt之间满足:
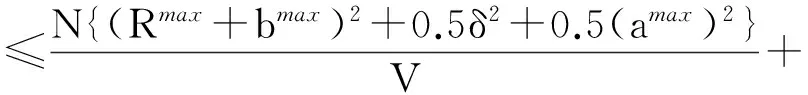
(17)
证明 ①用数学归纳法证明。显然Qi(0)+Zi(0)=0<Ωmax。假设当t=s时,命题成立,即Qi(s)+Zi(s)≤Ωmax。下面证明当t=s+1时,命题仍成立。
首先,分析Qi(s)+Zi(s)≤Vα+2bmax(Vα+1)-δ的情况。根据式(1)和式(6)可知,更新Qi(s)和Zi(s)时,它们的增加量分别不会超过amax和δ,故有Qi(s+1)+Zi(s+1)≤Qi(s)+Zi(s)+amax+δ≤Ωmax。
再分析Vα+2bmax(Vα+1)-δ δ+Qi(s)+Zi(s)>Vα+2bmax(Vα+1) (18) 令算法1的第2步中的子项为: fi(bi(t))=Vc(bi(t))+bi(t)2-bi(t){Qi(t)+δ+Zi(t)} 则fi(bi(t))在0≤bi(t)≤bmax处的一阶导数满足: Vα(2bi(t)+1)+2bi(t)-{Qi(t)+Zi(t)+δ} (19) 上式表明当Vα+2bmax(Vα+1)-δ 综上,Qi(t)+Zi(t)≤Ωmax, ∀i成立。 ②将命题①的结果代入引理1即可。 ③当Qi(t)+Zi(t)≤Vα-δ时,fi(bi(t))在0≤bi(t)≤bmax处的一阶导数满足: Vα(2bi(t)+1)+2bi(t)-{Qi(t)+Zi(t)+δ}≥0 上式表明当Qi(t)+Zi(t)≤Vα-δ时,fi(bi(t))在区间[0,bmax]上是单调递增的,故计算出bi(t)=0,即节点i的感知数据不会被丢弃。 (20) (21) 然后,根据本文提出的算法原则,即选择一种策略ρi(t)、γij(t)及bi(t)使得式(12)不等号右边的表达式最小,可得: (22) 式中:第3个不等式根据式(20)和式(21)、ε→0及0<δ≤E{ai(t)},∀i得到;第4个不等式根据0≤bi(t)≤bmax、0≤ρi(t)≤Rmax和0≤ai(t)≤amax得到;最后一个等式是由bmax、Rmax和amax及δ均为常数得到。将Φ(t)的表示式(11)代入上式,然后在式的两端取数学期望,则由迭代期望法则可得: (23) 再将上式两端除以TV,并从t=0到t=T-1依次相加,得: (24) 因为Qi(t)和Zi(t)有界,所以L(Θ(t))有界。因此,令T→∞时可得: (25) 综上,4个命题全部得证。 可见,当感知数据量ai(t),∀i服从独立同分布时,本文提出的算法使目标函数值与感知信息的最大收集时延存在一定的均衡关系,即感知信息的最大收集时延与V和1/δ成正比,而目标函数值与1/V和δ成正比。另外,由命题③可知,只要传感节点的数据感知速率不持续超出WSNs链路容量,通过设置合理的代价函数c(·)就能保证感知数据不会被丢弃,且在能耗与最大收集时延之间达到均衡。 3.1 仿真设置 为了验证本文提出的时变路由算法的可行性和有效性,本部分对算法进行仿真,仿真在MATLAB平台上进行。假设25个节点随机部署于500 m×500 m的正方形区域内,仿真区域的中心位置布置一个Sink节点,节点间的最大通信距离是140 m。本文产生的WSNs拓扑结构如图1所示。仿真中用到的其他共同参数:节点i在时间t的数据感知量ai(t)在区间[amin,amax]上随机产生;发送单位比特数据时电路电子能耗Eelec=50 nJ/bit;放大单位比特数据时所需要的电子能耗εfs=100 pJ/(bit/m2);单位时间内链路允许的最大传输量Rmax=1 000 bit;单位时间内允许节点丢弃的最大数据量bmax=amax。 图1 本文产生的WSNs拓扑结构 (26) 3.2 参数V与α对算法的影响 设置节点在单位时间内的最小和最大数据感知量分别是amax=200 bit和amin=100 bit,参数δ=0.6×amax。随着参数V和代价函数中的可调系数α的变化,感知数据存储队列、丢弃的总数据量、Sink节点接收到的总数据量及能耗等性能指标的变化分别如图2~图5所示。 图2 参数V和α对感知数据存储队列的影响 图3 参数V和α对丢弃的总数据量的影响 图4 参数V和α对Sink节点接收到的总数据量的影响 图5 参数V和α对能耗的影响 分析可得:①通过选取合适的V和α的值,保证了感知数据的丢弃量为0,且当α的值较大时,即提高丢弃感知数据的代价,较小的V值就能保证感知数据不被丢弃。如图3所示,在此仿真环境下,当α≥60时,只要调节V的值使得Vα≥600,感知数据就不会被丢弃。②仔细观察图2、图4和图5,当V值给定且调节α的值使得保证感知数据不被丢弃时,再增加α的值对网络的其他性能几乎没有影响。这表明在实际应用中,可以选取较大的α值,从而为V值的选取提供更大的范围。③根据图3~图5,当丢弃的数据量越多,需要发送给Sink节点的数据量就越少,所以经过能耗大的路径发送的数据量减少,从而使得发送单位数据到达Sink节点的平均能耗就降低。④随着V的增加,发送单位数据到达Sink节点的平均能耗就减少,但其代价是所有节点的感知数据存储队列平均值增加,即增大了数据到达Sink节点的平均时延。这和第2部分的理论分析结果是一致的。 图6 参数δ对感知数据存储队列的影响 3.3 参数δ对算法的影响 设置节点在单位时间内的最小和最大数据感知量分别是amax=200 bit和amin=100 bit,参数V=10及代价函数中的可调系数α=60。随着参数δ从0.2amax增加到amax,得到:①感知数据的丢弃量均为0。这表明只要确定了合适的V值和α值,参数δ值的变化几乎不会影响感知数据的丢弃情况;②如图6所示,所有节点的感知数据存储队列平均值减少,即降低了数据到达Sink节点的平均时延。又由于数据丢弃量均为0,在500个单位时间处,Sink节点接收到的总数据量是不断增多的,如表2中的第2行所示。特别地,当δ值增加到0.8amax时,稳定状态下的所有节点的感知数据存储队列平均值为0,即所有数据均被实时传输到Sink节点。当然,其代价是相比于δ≤0.6amax时的情况,发送单位数据到达Sink节点的平均能耗增加了约0.001 μJ。 从上述分析可知,能耗、感知数据的丢弃量及传输时延之间存在一定的均衡关系。因此应根据实际需求来确定参数V、δ及α的值。 表2 参数δ对Sink节点接收到的总数据量和能耗的影响 图7 不同的数据感知速率对感知数据存储队列的影响 3.4 本文算法与AVE算法的比较 设置节点在单位时间内的最小数据感知量是amin=0 bit,参数V=10、δ=0.6×amax及代价函数中的可调系数α=60,节点在单位时间内的最大数据感知量amax从100 bit逐步增加到500 bit。由图7和表3可知,①当amax≤200 bit时,稳定状态下的所有节点的感知数据存储队列平均值均为0,本文算法发送单位数据到达Sink节点的平均能耗略高于AVE算法;②当300 bit≤amax≤400 bit时,稳定状态下的所有节点的感知数据存储队列平均值在大部分时间为0,但会出现小波动,如图7中的黑色小圆圈所示。这是由于随着数据感知速量的增加,能耗小的路径上的链路承受力趋于饱和,本文算法试图等待在感知数据量较少的时间里再将数据沿着能耗小的路径传输到Sink节点,这正是本文算法的出发点之一,如第1部分所述。另外,本文算法发送单位数据到达Sink节点的平均能耗明显高于AVE算法,尤其当amax=400 bit时,本文算法发送单位数据到达Sink节点的平均能耗增加了达0.052 μJ;③当amax增加到500 bit时,节点的感知量超出了WSNs链路容量,故AVE算法无法得到可行解,而本文算法通过等待和丢弃少量数据量等策略,使得Sink节点接收到了95.44%的感知数据。 表3 不同的最大数据感知速率下,发送单位数据 可见,本文算法在节点感知数据量较低的情况下,能得到接近于AVE算法的路由结果,同时也能处理节点感知数据量较高使得AVE算法无法计算的情况。但当节点感知数据量较为均衡时,本文算法的性能欠佳。不过再次说明,实际中节点的平均感知速率是很难得到的。 本文考虑WSNs应用中监测环境具有随机性和不可预测性等因素,研究时变感知速率下的路由问题,提出了一种基于Lyapunov优化技术的时变路由算法来实时决策每条链路上的数据流量以及由于节点感知速率持续超出链路容量而不得不丢弃的感知数据量。理论分析与仿真实验均表明通过选取合适的参数V、δ及α值,可在能耗、感知数据丢弃量及传输时延之间达到一定的均衡。本文算法还能处理节点感知速率较高使得AVE算法无法计算的情况。下一步将结合Sink节点移动的方法,进一步研究优化算法在能耗、感知数据的丢弃量及传输时延等方面的性能。 [1] 何杏宇,周亦敏,杨桂松,等. 无线传感器网络能量感知增强树型路由协议研究[J]. 传感技术学报,2015(4):551-556. [2] Madan R,Lall S. Distributed Algorithms for Maximum Lifetime Routing in Wireless Sensor Networks[C]//Proceedings of the IEEE Global Telecommunications Conference,2004:748-753. [3] Hong Y,Xu J,Jiang C. Lifetime Maximization in Wireless Sensor Networks with Network Coding[C]//Proceedings of IEEE International Conference on Wireless Communications,Networking and Mobile Computing,Los Angeles:IEEE,2007:2527-2530. [4] Cheng M,Gong X,Cai L. Joint Routing and Link Rate Allocation under Bandwidth and Energy Constraints in Sensor Networks[J]. IEEE Transactions on Wireless Communications,2009,8(7):3770-3779. [5] 任条娟,杨海波,陈友荣. Sink 节点移动的无线传感网生存时间优化算法[J]. 传感技术学报,2012,25(5):683-690. [6] Yun Y S,Xia Y,Behdani B,et al. Distributed Algorithm for Lifetime Maximization in Delay-Tolerant Wireless Sensor Network with Mobile Sink[J]. IEEE Transactions on Mobile Computing,2012,12(10):370-375. [7] Yun Y S,Xia Y. Maximizing the Lifetime of Wireless Sensor Networks with Mobile Sink in Delay-Tolerant Applications[J]. IEEE Transactions on Mobile Computing,2010,9(9):1308-1318. [8] Wang Y,Tan H. Distributed Probabilistic Routing for Sensor Network Lifetime Optimization[J]. Wireless Networks,2016,22(3):975-989. [9] Kumar V,Kumar S. Energy Balanced Position-Based Routing for Lifetime Maximization of Wireless Sensor Networks[J]. Ad Hoc Networks,2016,52:117-129. [10] 薛亮,王燕龙,李志华,等. 无线传感器网络中基于数据融合的时变速率路由算法[J]. 微电子学与计算机,2015,32(12):130-135. [11] Hou Y T,Shi Y Y. Variable Bit Rate Flow Routing in Wireless Sensor Networks[J]. IEEE Transactions on Wireless Communications,2007,6(6):2140-2148. [12] Xue L,Yang B,Zhao J,et al. Joint Resource Reconfiguration and Robust Routing for Cognitive Radio Networks:A Robust Optimization Approach[J]. Wireless Communications and Mobile Computing,2015,15(5):848-867. [13] Neely M J. Stochastic Network Optimization with Application to Communication and Queuing Systems[M]. Morgan & Claypool,2010. [14] Yuanyuan Y,李亚宁. 无线可充电传感器网络[J]. 国外科技新书评介,2015(7):22-23. [15] 胡诚,汪芸,王辉. 无线可充电传感器网络中充电规划研究进展[J]. 软件学报,2016,27(1):72-95. Variable Bit Rate Flow Routing in Wireless Sensor Networks Based on Lyapunov Optimization* DONG Qifen*,ZHANG Qiqian (Department of Computer and Information Technology,Zhejiang Police College,Hangzhou 310053,China) Monitoring environment in the application of wireless sensor networks is always random and unpredictable,so the node sensing rate is usually time-varying and may exceed the link capacities at some time-slots. Pointing at this problem,a variable bit rate flow routing algorithm is designed in this paper. In the proposed algorithm,the routing problem with time variable sensing rate is described as a stochastic optimization model whose objective function is to minimize the weighted sum of time-average power consumption and the cost induced by discarding sensed data. The model is solved by Lyapunov optimization technique,and a routing method is proposed to determine the amount of data flowing through each link and to calculate the amount of data to be discarded when the node sensing rate continuously exceeds the link capacities in real time. Further,the condition under which the data will not be discarded is discussed and an explicit trade-off between the value of objective function and the worst-case delay of data transmission is obtained. Finally,simulation demonstrates the relationship among power consumption,the amount of discarded data and the data transmission delay. We also compare the performance of the proposed algorithm with AVE algorithm under different maximum node sensing rates. wireless sensor networks;variable bit rate flow routing;lyapunov optimization 董齐芬(1985-),女,博士,讲师,主要研究方向为无线传感网、优化算法,dongqifen@zjjcxy.cn; 张其前(1976-),男,博士,讲师,主要研究方向为计算机取证,控制理论、优化理论等。 项目来源:NSFC-浙江两化融合联合基金项目(U1509219) 2016-11-03 修改日期:2016-12-29 TP393 A 1004-1699(2017)05-0758-08 C:7230 10.3969/j.issn.1004-1699.2017.05.021

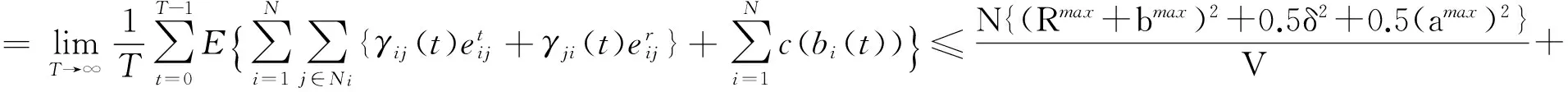
3 仿真实验
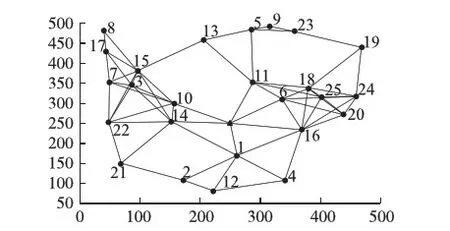




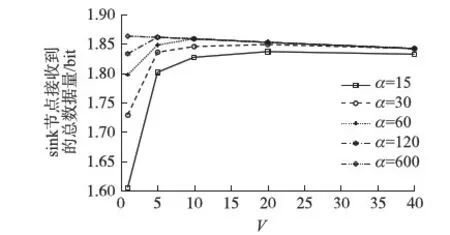


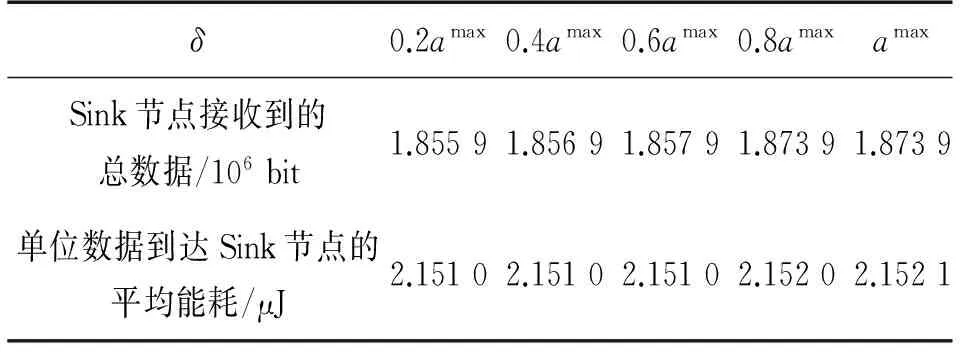


4 结语



