近程巡飞弹姿态控制优化仿真研究

黄 瑞，陈建辉，高 敏，陶贵明

(军械工程学院，石家庄 050003)

近程巡飞弹姿态控制优化仿真研究

黄 瑞，陈建辉，高 敏，陶贵明

(军械工程学院，石家庄 050003)

近程巡飞弹姿态控制系统是一个非线性、时变性及耦合性的复杂控制系统，是近程巡飞弹武器系统型号研制的关键技术之一;传统的PID控制在不同巡飞状态下调节稳定性较差、响应时间慢、影响姿态控制的稳定性和机动性;针对近程巡飞弹姿态控制系统中PID控制参数不可调，自适应、抗干扰性能较差等问题，引入了自适应模糊PID控制方法，使系统在不同巡飞姿态和干扰条件下能够实时整定PID的三个控制参数，提高系统的控制性能;在此基础上设计了近程巡飞弹的姿态角控制回路，并以俯仰角为例，在Matlab/Simulink平台下建立仿真模型，进行仿真实验;仿真结果显示，采用自适应模糊PID的控制方法，系统控制性能更好，抗干扰能力和自适应能力优于传统PID控制，减小了巡飞过程中姿态角的波动情况。

姿态控制；模糊控制；参数整定；抗干扰

0 引言

近程巡飞弹是无人机技术与精确制导弹药技术相结合的产物，近程巡飞弹作战半径较小，战场灵活机动性较高，可实现巡飞侦察、毁伤评估、精确打击、通信中继、目标指示、空中警戒等作战功能。飞行控制系统的设计是近程巡飞弹研发的核心技术之一[1]。当前关于飞行控制的理论研究已取得较多的成果，各种先进的智能控制算法层出不穷[2]。张希铭等利用模糊PID控制算法初步解决了球型机器人的平衡与运动控制问题，并通过仿真验证控制性能对环境具有更强的适应能力[3]。王安等分析了模糊PID控制的性能特点及优势，并在MATLAB/Simulink平台下进行了仿真分析，解决了模糊PID对动力系统的灵敏控制问题[4]。为提高飞行器姿态控制系统的鲁棒性和动态特性，刘鹏云等应用非光滑控制方法设计了连续的姿态控制律，并分别针对标称系统、参数不确定性和外部扰动等情形进行仿真，验证了控制系统的优越性[5]。其它的控制方法还包括反步法、自抗扰、遗传算法等。在姿态控制领域的研究存在两点不足：第一，先进的控制算法研究虽然较多，在实际应用使用较少；第二，在巡飞弹巡飞武器领域的研究极少。在这样的背景下，提出了模糊PID控制在巡飞弹姿态控制中的应用。

由于在巡飞控制过程中存在模型非线性、时变性及耦合性等特征，PID控制系统不便于调节控制参数，使系统的适应性差、抗干扰能力差、难以达到预想的控制效果[6]。模糊控制技术具有鲁棒性强、抗干扰能力强、适应性强的优点[7]。将模糊控制与PID控制结合起来，利用模糊控制对PID的参数进行在线调节，即体现PID控制器的动态跟踪品质和稳态性能，又体现模糊控制强鲁棒性的优点，使近程巡飞弹控制系统动态响应速度快，超调量小，稳定性更好[8]。该研究对于导弹、无人机、巡飞弹药等先进飞行器的飞行控制系统设计与实现具有一定的参考价值。

1 近程巡飞弹姿态控制数学模型

近程巡飞弹的飞行动力学模型是其飞行控制系统设计和实现飞行稳定与控制跟踪的基础。考虑到外界条件对控制系统的影响及控制系统本身的复杂性，建立数学模型时需要先作出飞行控制假设，忽略微小因素的影响，便于模型公式的推理。近程巡飞弹巡飞过程姿态的非线性动力学模型为:

(1)

式中,p、q、r分别为弹体角速度ω在机体坐标轴ox、oy、oz上的分量；Φ、θ、Ψ分别为滚转角、俯仰角及偏航角；L、M、N分别为弹体所受的滚转力矩，俯仰力矩、偏航力矩；Ix、Iy、Iz分别为弹体绕弹体坐标轴ox、oy、oz三轴的转动惯量，Ixz为惯性积。δe、δr、δa、δT分别为升降舵偏角、方向舵偏角、副翼舵偏角，发动机油门开度，是系统控制量，弹体所受力矩是控制量的函数。

通过小扰动法对姿态运动方程进行简化处理，把运动方程进行解耦处理，以短周期运动近似模态忽略一些次要条件可得到巡飞弹的纵向运动可得到系统的传递函数。

简化解耦后俯仰、偏航、滚转通道的传递函数如下：

(2)

式中,Kθ、Kψ、Kφ为俯仰、滚转、偏航通道的传递函数系数,Tθ、Tψ、Tφ为各通道时间常数,ξθ、ξψ、ξφ为各通道相对阻尼系数,T1θ、T1ψ、T1φ为各通道的气动力系数[9]。

2 模糊PID控制器设计

传统的PID能够在模型确定的控制系统中起到不错的控制效果，但在实际控制中，对于姿态控制这种非线性时变模型，PID控制的固定参数适应能力和抗干扰能力差，无法根据系统模型的变化达到最优控制效果。针对该问题，提出使用模糊控制技术对PID控制器的参数进行实时在线整定，增加系统的适应能力和抗干扰能力，提升控制器性能。

基于模糊PID的姿态回路控制原理是：首先找出PID控制器的3个参数Kp、Ki、Kd与姿态角误差e及姿态角速度误差Δe之间的模糊控制规律，然后根据模糊控制规律实时调整Kp、Ki、Kd的变化值，从而达到PID控制的参数自适应以满足不同的输入e、Δe对控制参数的要求，使PID控制器能够实现对姿态角的最优控制。

2.1 Fuzzy-PID控制器结构

Fuzzy-PID 控制器通过对系统的e和Δe进行实时的检侧，然后根据模糊控制的规律实时调整ΔKp、ΔKi、ΔKd的大小，进而调整PID的3个控制参数使其对不同的e和Δe具有自适应能力，改善系统的静动态性能。Fuzzy-PID控制器的结构原理图如图1所示。

图1 Fuzzy-PID原理图

2.2 模糊论域的划分

控制器两个输入量e和Δe的模糊论域分别设为[-3,3]和[-6,6],量化因子为ke和kec，分别取值为1和0.5。控制器的输出量ΔKp、ΔKi、ΔKd的模糊论域都取为[-10,10]，[-1,1]，[-1,1]。比例因子分别取值为4、2、2。把输入量与输出量的模糊论域都划分为7各模糊子集：{负大、负中、负小、零、正小、正中、正大}。为了设计与分析的方便，用X={NBNMNSZOPSPMPB}，分别代表七个子集。

2.3 模糊控制的隶属度函数

设计模糊控制器时，若模糊规则已定，控制器的性能就取决于各模糊子集的隶属度函数。模糊控制器常用的隶属度函数包括：三角形隶属度函数、梯形隶属度函数、高斯分布函数、S型曲线函数等类型。在系统设计时根据需要可选择某个隶属度函数，也可以通过多种隶属度函数组合的形式构成系统的隶属度函数。

隶属度函数的确定：设输入量和输出量负大(NL) 模糊矢量用Z-型隶属度函数(zmf)，正大(PL)模糊矢量用S-型隶属度函数(smf)，其余模糊矢量选用三角形隶属度函数(trimf)。以Δe为例，其对应隶属度函数如图2所示，e、Δkp、Δki、Δkd对应的隶属度函数同Δe相似，论域不同。

图2 Δe的隶属度函数

2.4 模糊规则的确定

依据Kp、Ki、Kd对PID控制输出的影响情况，并结合技术人员的知识和实际操作经验等因素，总结出系统在参数整定过程中，对于不同的误差和误差变化率，PID的参数整定规则如下：

1)当|e|较大时，为了提高系统的跟踪特性，应选取较大的Kp和较小的Kd值，较大的Kp值容易引起系统出现较大的超调量，因此应充分限制积分作用对超调量的贡献，常取值Ki=0。

2)当误差|e|和|Δe|大小适中时，在此种状态下，Kd的取值对系统的性能影响十分明显，因此Kd的值应较小；为使系统具有较小的超调量，Kp的值应当小一些，Ki的取值应适当。

3)当|e|较小时，为使系统具有较好的稳态性能，Kp和Ki的值都应该适当大一些，同时为避免控制系统在稳定点附近发生振荡，并且考虑到系统的抗干扰能力，当|Δe|较大时，Kd可取较小的值，当|Δe|较小时，Kd应取值应相对大些，通常情况下，Kd取值应该适中。

4)当|Δe|较大时，为保证系统响应速度和稳定精度，防止过大超调，应选较小和适中的Kp值，尽可能选较小的Ki值。

表1 模糊控制规则表

5)当|Δe|较小时，为保证系统具有较快的响应速度，应取较大Kp、Ki值和适当Kd值。

由上述模糊控制规则及专家经验可得模糊控制规则表如表1所示。

应用if、then、and等关键词设计参数调节规则表。共包括49条语句如下所示：

1)if(eis nl)and (Δeis nl) then (Δkpis pl)(Δkiis nl)(Δkdis pm);

2) if(eis nm)and (Δeis nm) then (Δkpis pl)(Δkiis nm)(Δkdis ps);

……

49)if(eis pl)and (Δeis pl) then (Δkpis nl)(Δkiis pl)(Δkdis pp);

图4 俯仰角控制系统仿真图

根据模糊控制规则表，查找参数调整值代入下式，计算修正后的PID控制参数：

(3)

3 数字仿真实验

3.1 模糊PID姿态控制系统设计

姿态角控制系统结构图如图3所示。

图3 姿态角控制系统结构图

整个控制系统由外回路和内回路两个反馈回路构成，外回路是姿态角反馈，内回路是姿态角速率反馈。姿态角速率反馈回路的作用是增加系统的阻尼特性，以修正巡飞弹弹体阻尼较小的不足[10]。为提升系统性能在姿态角速率反馈回路中增加洗出网络，其作用是在近程巡飞弹爬升或空中盘旋转弯时清除阻尼信号。如果缺少洗出网络，阻尼回路在抑制高频干扰的同时也会抵消控制回路的响应信号，将阻尼回路的稳态输出变为阻碍因素[11]。洗出网络的形式为：

(4)

舵机的传递函数为：

(5)

其中，经过反复实验测试调整后，在此洗出网络t取值选择0.3，反馈增益取值Kc=0.33。

为分析所设计的近程巡飞弹姿态角控制回路的控制性能，引入传统PID控制进行对比分析。基于以上的近程巡飞弹的数学模型、舵机模型、洗出网络和模糊控制器设计，结合姿态角控制系统结构图，在MATLAB的Simulink仿真环境下建立近程巡飞弹俯仰角控制的常规PID控制和模糊PID参数自整定控制的系统仿真模型如图4所示。

3.2 仿真实验及结果分析

由于篇幅有限，以俯仰通道为例测试所设计的姿态角控制器的性能。

本文以某型近程巡飞弹研究对象，巡飞弹质量为15 kg、长度为1.5 m、翼展1.2 m、气动弦长为0.4 m、巡飞速度80 m/s、巡飞高度为400 m。代入风洞实验所得气动数据参数，后得到俯仰角对升降舵的传递函数如下式所示：

(6)

分别进行了正常状态下、模型结构变化时、受干扰情况下系统阶跃响应的仿真实验，并对比常规PID和Fuzzy-PID 的仿真曲线分析系统性能。

仿真1：正常巡飞状态下俯仰角控制系统的阶跃响应，其结果如图5所示在经过反复调整后PID控制与模糊PID控制的费用速度与稳态性能差别不大，但模糊PID控制的调节时间为1.2 s，传统PID的调节时间为1.6 s，模糊PID控制的性能更优越。

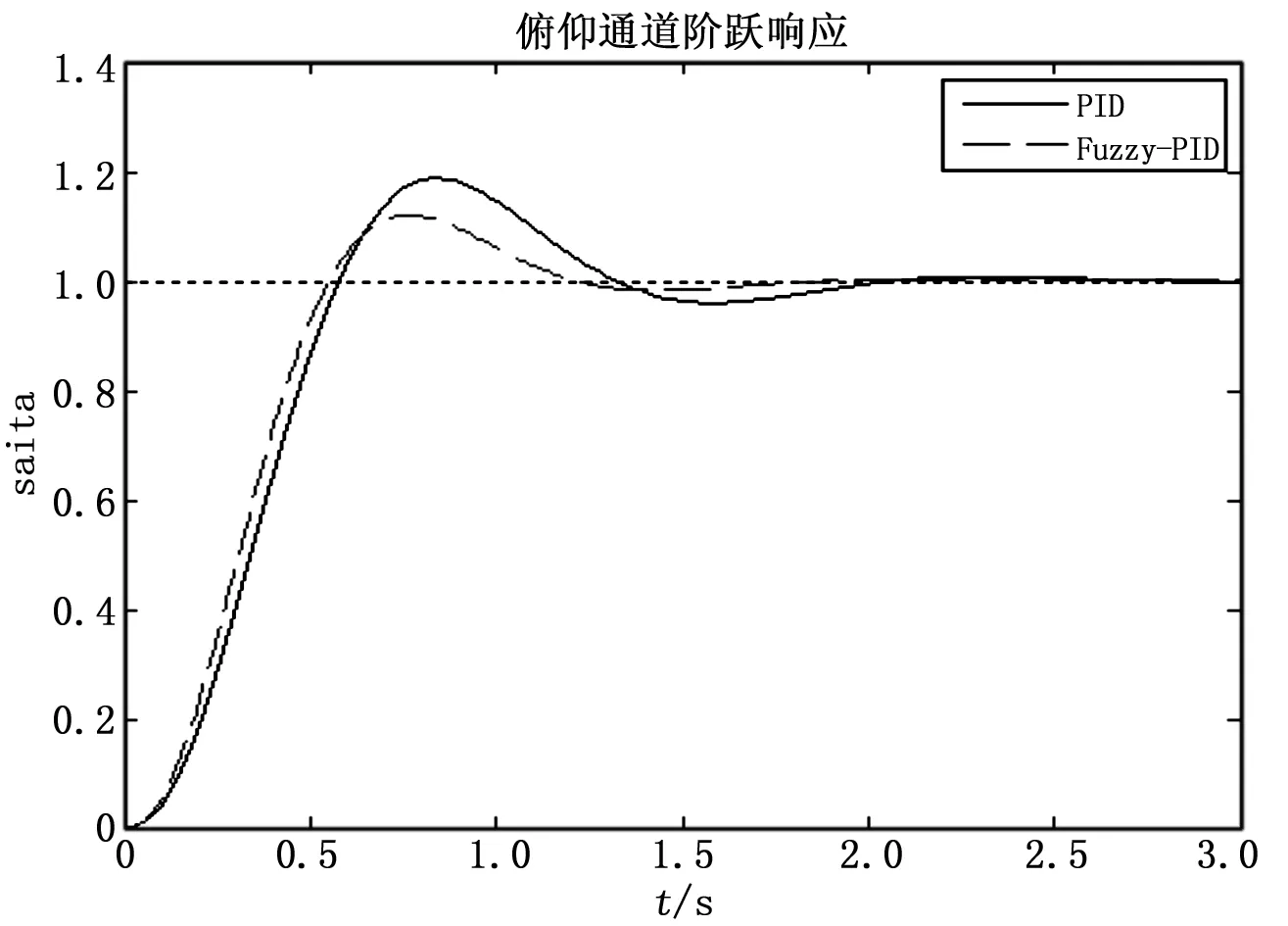
图5 正常状态下阶跃响应

仿真2:用下式的传递函数代替系统原传递函数，模拟系统模型结构变化时控制器的控制性能，变化的传递函数为:

(7)

如图6所示，模型变化引起了控制器性能的明显变化，对比模糊PID控制与传统PID控制发现，模糊控制的适应能力更强，在传统PID控制超调量过大，为46%发生激烈振荡的情况下，模糊PID控制的超调量职位20%，控制器性能明显得到优化。

图6 结构变化时阶跃响应

仿真3：在控制器的输出端添加起始时间t=3，幅值为1的阶跃信号模拟所受的干扰信号。其响应曲线如图7所示，对比与传统PID控制，在模糊PID控制系统中干扰对系统的响应较小，并且系统更快的完成调节，补偿干扰信号的影响。

图7 干扰状态下阶跃响应

由以上仿真实验可知，所提出的模糊PID控制相比于传统PID控制具有更好的自适应能力和抗干扰能力，系统控制性能更好，应用模糊PID控制能够有效完成对近程巡飞弹的姿态角进行控制。

4 结束语

本文以近程巡飞弹数学模型为基础，对其控制系统进行了分析设计，针对常规PID参数不可变、适应能力差的缺点，设计了模糊自适应PID控制器对近程巡飞弹实施姿态控制。该控制方法充分发挥了PID控制和模糊控制的优势，可实时调整控制系统的参数，大大提高系统的适应能力和抗干扰能力。仿真结果表明，所设计的控制器在适应能力，抗干扰能力等方面都优于传统PID控制，改进的自适应模拟PID控制器能够大大减小系统姿态角的波动情况，对姿态的稳定控制具有现实的意义。

[1] 黄 瑞,高 敏,陈建辉. 轻小型巡飞弹及其关键技术浅析[J]. 飞航导弹, 2015(12):16-19.

[2] 范彦铭.飞行控制技术与发展[J]. 飞机设计,2012(4):33-37.

[3] 张希铭,曲仕茹,马志强. 四旋翼飞行器模糊滑膜控制器设计与仿真[J]. 飞行力学,2014(5):441-445.

[4] 王 安,杨青青,闫文宇. 模糊自整定PID控制器的设计与仿真[J]. 计算机仿真,2012(12):427-432.

[5] 刘鹏云,孙瑞胜. 一种改进的巡飞弹侧向运动解耦设计[J]. 飞行力学, 2011(6):52-56.

[6] 汪洋亮,王国胜,李中良. 基于PID的高速无人机高度控制系统设计[J]. 舰船电子工程,2009(2):163-166.

[7] 韩俊峰,李玉慧. 模糊控制技术[M]. 重庆:重庆大学出版社,2003.

[8] Zhang K R, Pan A Q, Chu X J. MPPT research based on fuzzy adaptive PID control[J]. Journal of Measurement Science and Instrumentation, 2012(4):389-392.

[9] 肖培春. 基于模糊控制方法的巡飞弹飞行控制系统设计与仿真研究[D]. 南京：南京理工大学,2011,12.

[10] 张 聚. 基于MATLAB的控制系统仿真及应用[M]. 北京：电子工业出版社,2012.

[11] 孙 博. 无人侦察机自动驾驶仪控制系统研究[D]. 哈尔滨：哈尔滨工程大学,2012.

Optimization and Simulation of Short-range Loitering Missile Attitude Control System

Huang Rui, Chen Jianhui, Gao Min, Tao Guiming

(Ordnance Engineering College, Shijiazhuang 050003, China)

This paper focuses on Attitude control system of proximity patrol missile which is nonlinear, time-varying and complex coupling control system, and it is one of the key of short-range patrol missile weapon system developed. Traditional PID control is less stable and have slow response time, affect the stability and maneuverability of attitude control. Due to parameters of PID control are not adjustable, poor adaptive anti-jamming performance issues for short-range missile patrol attitude control system. An adaptive fuzzy PID control method is provided to improve the control system performance by tuning PID parameters real-time. Attitude angle control loop of short-range patrol missile is designed, and taking pitch angle for example, build the simulation model in Matlab / Simulink platform, by comparing the traditional PID control, analysis the controller performance. The simulation results show that the adaptive fuzzy PID control method, the system control performance is better, anti-interference ability and adaptive ability is superior to the traditional PID control, which reduces the fluctuation of loitering during attitude angle.

attitude control; fuzzy control; parameter tuning; anti-interference

2016-10-24；

2017-01-05。

装备预研共用技术基金项目(9140A05040213JB34069)。

黄 瑞(1991-)，男，硕士研究生，主要从事精密仪器与微系统方向的研究。

1671-4598(2017)05-0119-04

10.16526/j.cnki.11-4762/tp.2017.05.033

V249.21

A