基于蒙特卡罗法的平面度测量不确定度评定
吴呼玲
(陕西国防工业职业技术学院 机械工程学院,西安 710300)
基于蒙特卡罗法的平面度测量不确定度评定
吴呼玲
(陕西国防工业职业技术学院 机械工程学院,西安 710300)
形位误差的测量不确定度评定是目前测量领域研究的热点;但由于其测量的复杂性和测量结果评定的多样性,导致在实际测量结果中形位误差测量的不确定度评定成了难题;为此,根据形状误差评定准则,选取最小二乘法建立数学模型,确定形状误差数学模型中各参数值的传递系数和单点不确定度,并分析具体的测量方法和测量过程中的不确定度来源,根据传统的GUM法对其进行不确定度评定;然后采用蒙特卡罗伪随机数的方法来模拟实际测量数据,从而得到平面度误差的不确定度;通过设置实验对比,验证了蒙特卡罗法评定平面度不确定度的可靠性和准确性;该方法不需要求出数学模型中的传递系数,利用MATLAB软件很容易实现,为平面度误差测量结果不确定度评定提供了更加简便的方法,值得推广和应用。
蒙特卡罗;平面度误差;不确定度;最小二乘法
0 引言
平面度测量误差的评定是测量领域中经常遇到的误差评定项目。因此,准确、快速的评定平面度测量结果的不确定度成为一个重要的课题。随着测量不确定度在我国受到越来越高的重视,对于从事测量的专业技术人员来讲,测量不确定度成为了测量领域研究的热点[9]。然而其复杂性和多样性的特点,致使不确定度的评定难以评估。
蒙特卡罗法[1]又称统计模拟法、随机抽样技术,是使用随机数(或伪随机数)来解决问题的一种方法。它的基本思想是,为了所求问题的解是某个随机变量的数学期望时,通过某种实验的方法,得出该随机变量若干个具体观察值的算术平均值,通过它得到问题的解。本文利用蒙特卡罗法进行平面度测量结果不确定度的评定,利用MATLAB软件产生一组服从测量值分布概率的随机数组来模拟测量值,从而利用统计方法来进行不确定度评定。为了验证此方法的准确性和可靠性,根据不确定度合成公式再次进行评定,求出传递系数和各参数的单点测量不确定度,计算出平面度误差的测量不确定度。实验结果表明,蒙特卡罗法评定平面度测量不确定度准确、快捷、简单、可靠,解决了形位误差测量不确定度评定的复杂性和多样性,为其他形位误差简单、便捷的评定提供了评定方案。
1 平面度误差模型
本文用最小二乘法原理建立数学模型。
(1)
(2)
(3)
(4)
2 平面度测量结果不确定度评定
2.1 蒙特卡罗法评定平面度测量结果不确定度
根据平面度最小二乘法评定的误差数学模型,利用蒙特卡罗伪随机数的方法产生服从期望为各参数的测量值,方差为各参数的单点标准不确定度的正太分布的随机值序列,得出平面度误差测量不确定度。
具体操作的方法和步骤如下[7]:
1)分析测量过程中不确定度来源。确定分布区间和分布类型,确定因子K的取值,计算出各个方面不确定度来源对应的不确定度数值。为后续数组中的方差提供依据(方差为各参数的不确定度)。
2)确定平面度误差模型(公式4)中的参数:xM;xL;yM;yL;zM;zL;a;b的期望和方差(期望为各参数的测量值,方差为各参数的单点标准不确定的度)。
3)以xM;xL;yM;yL;zM;zL;a;b参数的期望和方差生成八维随机数来模拟平面度误差的测量值,样本容量为M,采用大样本进行平面度误差的测量不确定度评定。生成的八维随机数分别为:xM1,xM2,xM3,……xMM;xL1,xL2,xL3,……xLM;yM1,yM2,yM3,……yMM;yL1,yL2,yL3,……yLM;zM1,zM2,zM3,……zMM;zL1,zL2,zL3,……zLM;a1,a2,a3,……aM;b1,b2,b3,……bM;
4)根据以上随机序列,带入(公式4)中平面度误差模型,求出M个平面度误差f的值,根据这组f的值,构造一个概率分布。判断分布类型求出方差,即为所要求的平面度误差测量标准不确定度。
2.2GUM法评定平面度测量结果不确定度
1)求出(4)式中平面度误差模型各参数的传递系数[3]:
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
2)各参数测量不确定度分别为:
平面度测量不确定度的分析,只需考虑分析z的不确定度即可[4]。z值的测量不确定度等于单点测量不确定度,即u(zM)=u(zL)=u0。而a和b的不确定度比较复杂,需要进行以下推导得到。
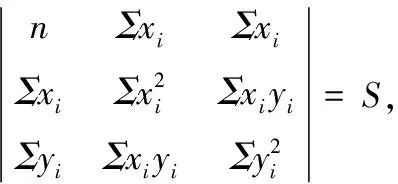
因此,
u(zM)=u(zL)=u0
(13)
(14)
(15)
将以上平面度误差模型各参数的传递系数(公式9~12)和各参数单点测量不确定度(公式13~15)带入不确定度合成公式16中,即可得到平面度误差测量不确定度评定结果:
uf=
(16)
3 实验数据分析及应用
使用爱德华公司的MQ686型三坐标测量机对一块平板进行平面度测量和评定。将被测平板放置于三坐标测量机的测量平台上,并使被测工件的长边平行于X轴,然后对平面度误差进行测量。被测工件长度80 mm,在X轴方向均匀取6个点,每个点间隔10 mm进行坐标测量,共测3行数据,即在被测平面上取3行6列共18个数据,布点情况[5]如图1所示,测量结果如表1所示。
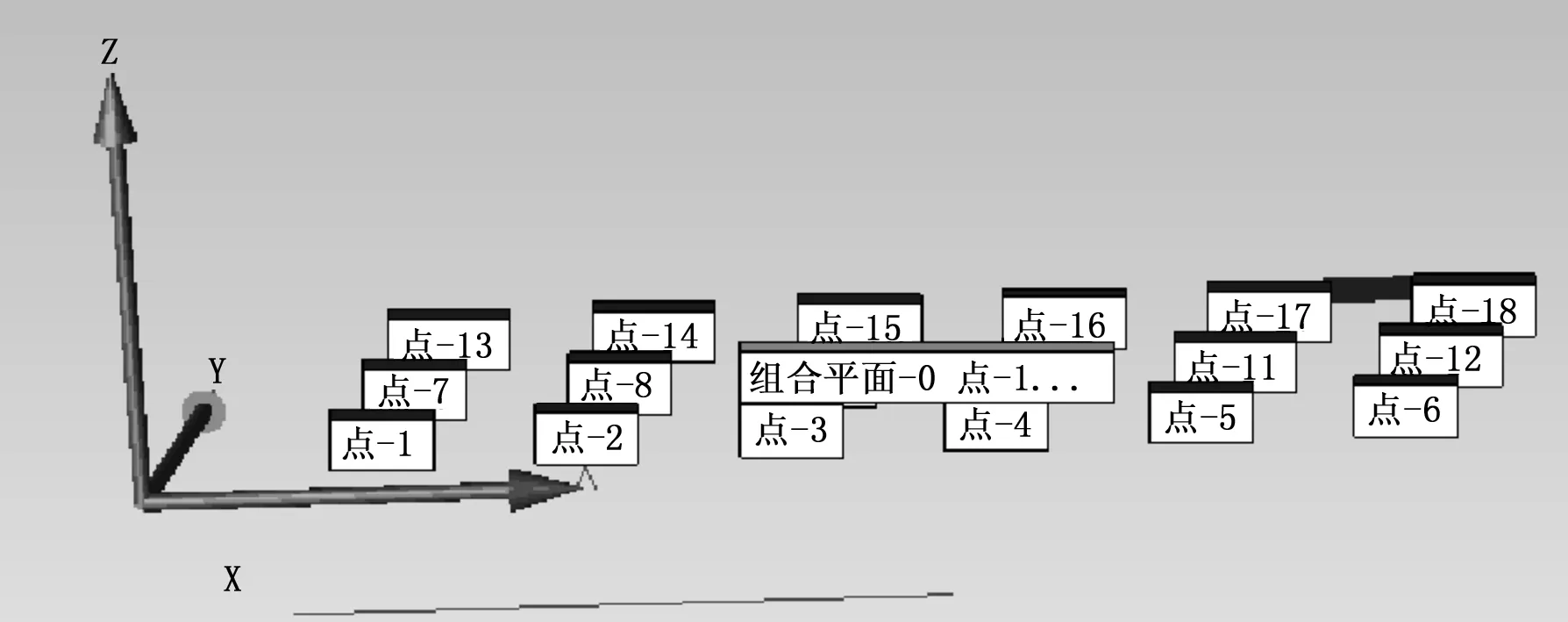
图1 三坐标测量机测量平板平面度的布点情况
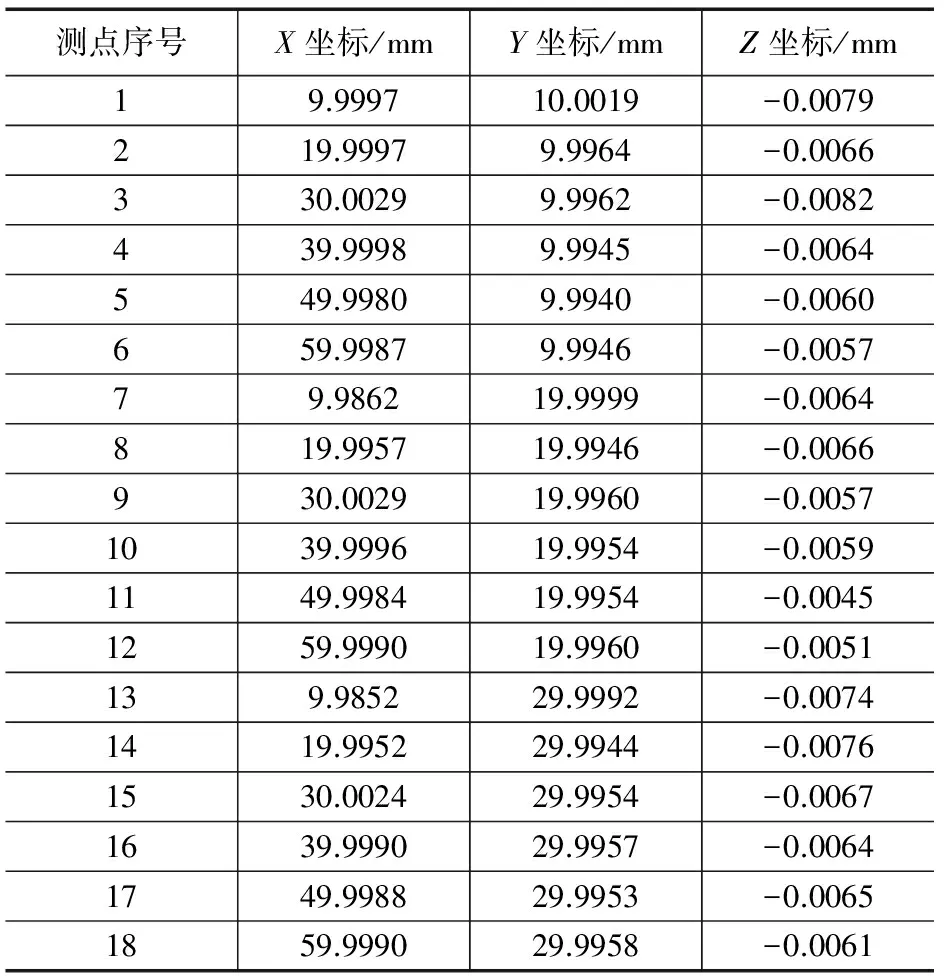
测点序号X坐标/mmY坐标/mmZ坐标/mm19.999710.0019-0.0079219.99979.9964-0.0066330.00299.9962-0.0082439.99989.9945-0.0064549.99809.9940-0.0060659.99879.9946-0.005779.986219.9999-0.0064819.995719.9946-0.0066930.002919.9960-0.00571039.999619.9954-0.00591149.998419.9954-0.00451259.999019.9960-0.0051139.985229.9992-0.00741419.995229.9944-0.00761530.002429.9954-0.00671639.999029.9957-0.00641749.998829.9953-0.00651859.999029.9958-0.0061
3.1 不确定度来源分析[8]
本次实验采用的MQ686型全封闭框架移动桥式三坐标测量机,其量程范围是:X600 mm,Y800 mm,Z600 mm,该仪器处于良好的工作状态,室内空调已经连续运行一周,使被测平板和三坐标等温,测量人员在1小时后进行测量工作。因此,可以忽略温度、湿度等环境带来的影响。其测量不确定度主要来自以下几个方面:
1)重复性引起的不确定度分量[10]。
三坐标测量机的重复性测量引起的不确定度,在平面度的测量不确定度的评定过程中是一个重要的因素。在平面度测量过程中,平板的长边是平行于X轴放置的,短边是平行于Y轴的,所以影响平面度误差的主要因素是Z轴的坐标值。因此,在评定重复性引入的不确定度过程中,只需要考虑Z轴坐标测量的重复性误差。
在测量的18个点中,选取3个点(1点、6点和15点)进行重复性测量实验,利用贝塞尔公式求出各点的重复性误差,取这三个点中重复性测量引起的不确定度的最大值,作为三坐标测量机的重复性引起的不确定度。
选取1点重复测量10次的测量数据为:
-0.0082;-0.0079;-0.0081;-0.0083;-0.0081,
-0.0078;-0.0076;-0.0082;-0.0079;-0.0075

u6=σ6=0.074 μm;u15=σ15=0.067 μm;
取最大值作为重复性所引起的不确定度,因此三坐标测量机的重复性测量引入的不确定度为u重复=0.085μm。
2)示值误差引入的不确定度分量。
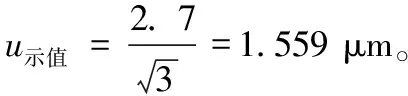
3)测量力引入的不确定度分量。
在测量中测量力调节至很小,可忽略测量力引起的零件弹性变形。因此,测量力的影响带来的不确定度分量为u力=0。
4)三坐标测量机分辨力引入的不确定度分量。
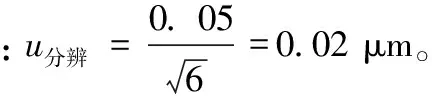
5)温度引入的不确定度分量。
在测量过程中,实验室空调已经连续运行了一周,被测件、三坐标和测量人员都在等温后进行测量工作。因此,测量力的影响带来的不确定度分量为u温度=0。
根据以上分析,直线度的单点测量不确定度为:
3.2 平面度误差计算
依据表1中的测量数据,带入公式(1~3),借助MATLAB软件求出a=3.551696623161069e-05、b=8.394157412702668e-07、c=-7.687578147000283e-03,可得最小二乘平面为z=(3.55e-05)x+(8.39e-07)y-(7.69e-03)。然后求出各测点到最小二乘平面的距离,计算结果如表2所示。

表2 各测点到最小二乘平面的距离
由表2可知,距离最小二乘平面最高的点是测点11(在此称为最大距离的点),对应的点坐标为(xM,yM,zM)、最低的点是测点3(在此称为最小距离的点),对应的点坐标为(xL,yL,zL)。将各参数带入平面度误差模型公式(4)中,则平面度误差值为:
2.981427013954202e-03mm=2.98μm
3.3 蒙特卡罗法的不确定度估算
利用MATLAB软件中的normrnd函数[6]生成服从正态分布的八维随机数,每一维数组的期望分别为各参数测量值,方差分别为各参数的不确定度,并且服从正态分布,即为:
[xM1,xM2,xM3,……xMM] ~N(49.9984mm,1.56μm);
[xL1,xL2,xL3,……xLM] ~N(30.0029mm,1.56μm)
[yM1,yM2,yM3,……yMM] ~N(19.9954mm,1.56μm)
[yL1,yL2,yL3,……yLM] ~N(9.9962mm,1.56μm)
[zM1,zM2,zM3,……zMM] ~N(-0.0045mm,1.56μm)
[zL1,zL2,zL3,……zLM] ~N(-0.0082mm,1.56μm)
[a1,a2,a3,……aM] ~N(3.551696623161069e-05 mm,1.767929943168856e-04)
[b1,b2,b3,……bM] ~N(8.394157412702668e-07mm,4.420132407275619e-04)
样本容量为M=10 000。由于样本很大,这里不予列出。根据所得随机数,求出10 000个f的值后,构建出平面度误差概率分布,其概率分布根据MATLAB中的直方图(横坐标为平面度误差值,纵坐标为其分布概率)来构建,求出这组数据的期望和方差,即为平面度误差和平面度测量不确定度,分别求得:
平面度误差:f=2.966479016299404e-03 mm=2.97 μm;
平面度测量不确定度:uf=6.036951149940499e-03 mm=6.04 μm;
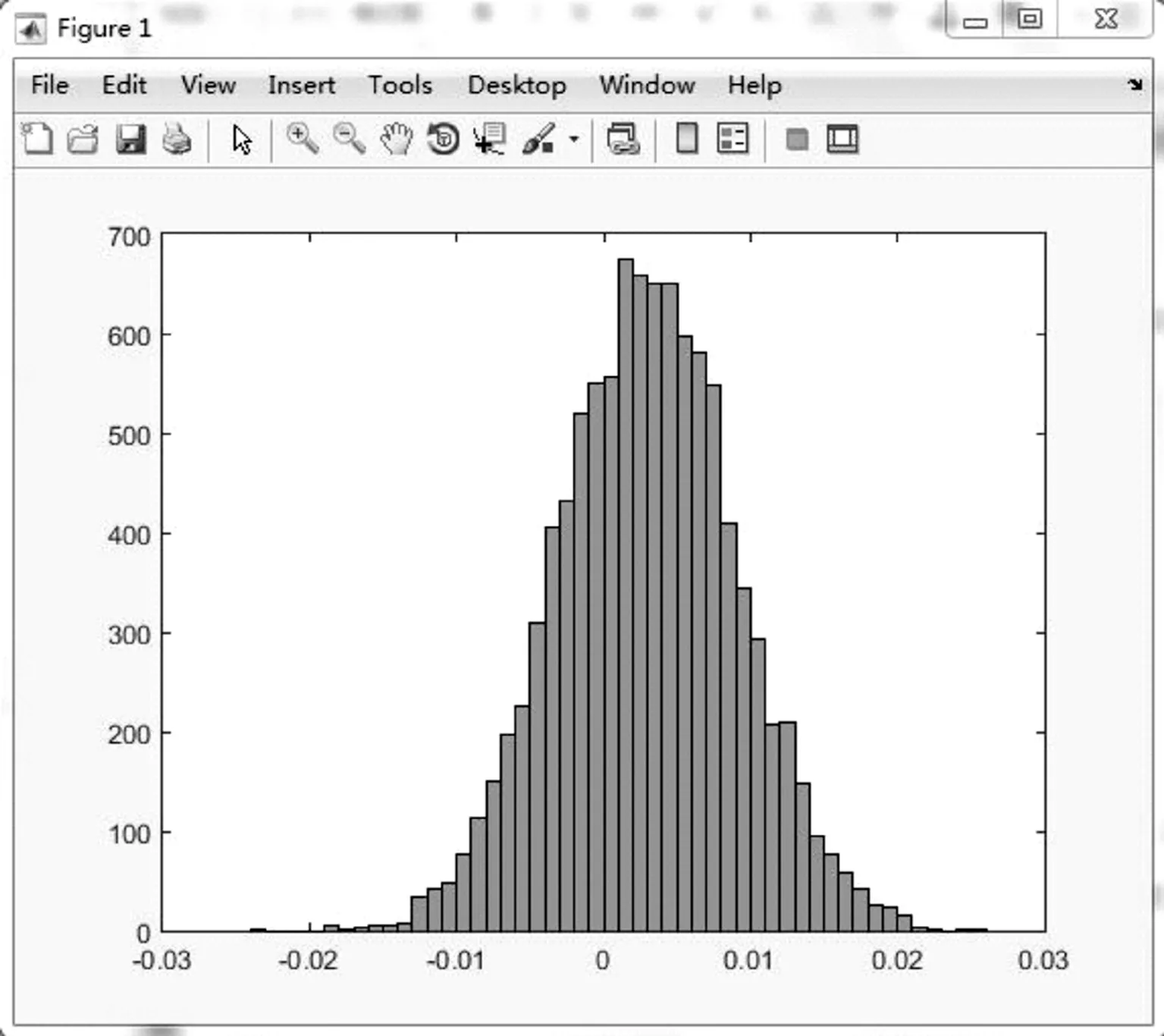
图2 平面度误差的概率分布
3.4 GUM法的不确定度验证
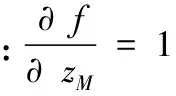
q=3.599307000000000e+02;u=2.729853448666000e+04;
v= 8.397192341290000e+03;w=1.259620107763000e+04;
S=1.134251187913089e+08根据公式(16)计算出平面度测量不确定度结果:
uf=6.074399101030872e-03 mm=6.07 μm
3.5 结果比较

表3 两种方法计算的平面度误差和评定的测量不确定度结果
4 结语
通过表3数据比较可知,用蒙特卡罗法进行平面度不确定度评定是可靠的。通过GUM法验证,两者结果几乎相同,而且蒙特卡罗法比GUM法评定结果更加准确。因此,通过实验验证,蒙特卡罗法评定平面度不确定度以评定结果精度高、计算快捷,简便、不必计算偏导数、不受模型复杂性的影响而凸显出它的优势。为以后其他形位误差测量不确定度的评定和其他数据处理领域的应用奠定了一定的基础,具有非常广泛的应用前景和工程实用价值。
[1] 周桃庚.用蒙特卡洛法评定测量不确定度[M].北京:中国质检出版社 2013.
[2] 倪骁骅.形状误差评定和测量不确定度估计[M].北京:化学工业出版社,2008.
[3] JJF1059.1-2012《测量不确定度的评定与表示》[S].
[4] 倪骁骅,黄晓峰,葛友华 平面度误差最小区域评定结果不确定度估计[J].盐城工学院学报(自然科学版),2006,19(2):5-8.
[5] 王金星,蒋向前,马利民,等.平面度坐标测量的不确定度计算[J].中国机械工程,2005,16(19):1701-1703.
[6] 王 伟,宋明顺、陈意华. 蒙特卡罗方法在复杂模型测量不确定度评定中的应用[J].仪器仪表学报,2008,29(7):1446-1449.
[7] 连慧芳,陈晓怀.基于蒙特卡罗方法的圆度测量不确定度评定[J]. 工具技术,2010,44(6):82-84.
[8] 王东霞,宋爱国.基于三坐标测量机的圆度误差不确定度评估[J].东南大学学报(自然科学版),2014,44(5):952-956.
[9] 陈怀艳,曹芸,韩洁.测量不确定度的发展和应用研究[J].宇航计测技术, 2014,10,34(5):65-70.
[10] 费业泰.误差理论与数据处理[M].北京:机械工业出版社, 2012.
Uncertainty Evaluation of Flatness Measurement Based on Monte Carlo Method
Wu Huling
(School of Mechanical Engineering, Shaanxi Institute of Technology, Xi’an 710300, China)
Evaluation of measurement uncertainty of shape and position error is a hotspot in the field of measurement. However, due to the complexity of measurement and the diversity of measurement results, the uncertainty of the measurement of the shape and position error in the actual measurement results has become a difficult problem. Therefore, according to the evaluation criterion of shape error, establish mathematical model adopting least squares method, determining the transfer coefficient of each parameter value of the shape error mathematical model and single point uncertainty, and uncertainty analysis of measurement methods and the specific process of the source, according to the traditional GUM method for uncertainty evaluation. Then the Monte Carlo pseudo random number method is used to simulate the actual measurement data, thus the flatness error uncertainty is obtained. The reliability and accuracy of Monte Carlo method to evaluate flatness uncertainty are verified by setting experimental comparison. This method does not need to calculate the transfer coefficient of mathematical model, it is easy to realize by using Matlab software, and provides a more convenient method for the uncertainty evaluation of flatness error measurement results.
Monte Carlo method;flatness error;uncertainty;least square method
2016-12-01;
2017-01-05。
陕西国防工业职业技术学院2016年科研项目(Gfy16-03)。
吴呼玲(1979-),女,陕西临潼人,讲师,硕士,主要从事机械产品检验检测、误差理论与数据处理、机械设备状态监测等方向的研究。
1671-4598(2017)05-0262-04
10.16526/j.cnki.11-4762/tp.2017.05.072
TH124
A

