土壤介电常数的多因素模型研究

牛旭+徐爱英+唐玉荣+杨瑛+胡芸莎

摘要：利用LCR数字电桥测量仪及自制加持平行电极板，测量10、100、1 000 kHz条件下土壤的相对介电常数与3种主要影响因素之间的变化规律。采用多元线性回归分析原理及模型，结合土壤相对介电常数的实测数据，运用SPSS软件对3种主要影响因素进行多元回归分析，得到了各因素与相对介电常数之间的相关关系及权重。结果表明，含水率、容重和温度与土壤相对介电常数显著相关（P<0.05），其中含水率和温度与土壤相对介电常数极显著相关（P<0.01）；利用多元线性回归建立不同测试频率下土壤相对介电常数与含水率、容重、温度3因素的回归方程，且权重的大小顺序始终为容重>温度>含水率。

关键词：介电常数；影响因素；相关性；多元线性回归；模型检验

中图分类号： S151.9+2文献标志码： A文章编号：1002-1302（2017）07-0258-03

土壤是地球陆地表层能够生长绿色植物的多空孔隙结构介质，通常由矿物质、有机质、水和空气组成[1]。土壤介电常数是指土壤在极化电场下对外电场的响应，它能够反映土壤品质与性质等众多物理信息[2]。国内外学者在土壤介电特性方面做了大量的研究。例如，Topp等给出了土壤介电常数与土壤含水率的经验模型[3]；由于原始的Topp模型缺乏物理机制，它的实用性受到一定的限制，Jackson等考虑了土壤容积、黏粒含量、有机质含量对土壤介电常数的影响，建立了半物理半经验的Topp模型[4]；康学远等研究出了土壤介电常数与含水率关系的一种模型[5]；朱安宁等对不同类型土壤介电常数与体积含水量关系进行了研究[6]；Velzquez-Martí等测定了农业土壤介电性质[7]；土壤介电常数与频率、温度、容积密度的关系也有不少的研究[8-11]，但含水率、容重、温度对土壤介电常数影响权重大小的研究却鲜有报道。本研究选用土壤含水率、温度和容重3因素进行土壤相对介电常数的研究，通过SPSS软件进行数据分析，得到影响土壤介电特性各因素之间权重大小的关系，通过多元线性回归方程找到土壤相对介电常数的最佳回归方程。

1多元回归分析数学原理与模型

多元线性回归是研究一个因变量与多个自变量之间的线性关系的统计分析方法。其基本目的是用一个自变量（x1，x2，…，xk）的数值估计另一个因变量（y）及其变异性的统计分析方法。总体线性回归模型为

式中：y为因变量；β0为模型常数项；βk为回归系数；xk为自变量。

样本线性回归方程为

式中：b0为常数项，表示当所有自变量为0时y的总体平均值的估计值；bk是βk的估计值，自变量xk的偏回归系数，表示当方程中其他自变量保持不变时，自变量xk每改变1个单位时y平均变化的单位数。

多元线性回归不仅需要进行回归系数的检验，估计回归系数的置信区间，进行预测与假设检验等方面的讨论，还需要考虑各个自变量之间的关系，如它们之间是否存在共线性的问题[12]。

Shang等在200～400 MHz频率范围内研究黏土试样的相对介电常数和介质损耗与不同含水率、密度、孔隙流体盐度的相关关系并建立多元线性回归模型[13]。Shi等研究比较了多元线性回归、偏最小二乘回归和支持向量机回归估计土壤全氮含量的优劣性[14]。Bilgili等研究了多元回归和人工神经网络模型对预测土壤温度和气象变化量之间的相关关系和回归方程[15]。周晨等利用多元线性回归模型对东北地区需水量进行了分析和检验[16]。黄安等利用多元线性回归分析集成所有成土因子对土壤养分进行了空间分布预测[17]。

2材料与方法

2.1样品制备

本研究土壤样品取自新疆阿拉尔市十团未耕作棉花地。土壤自然风干后，将干燥的土壤研磨后用18目筛子（孔径 1 mm）过筛，然后将土壤在105 ℃的烤箱中烘14 h，干燥后的土壤样品装入密封塑料袋保存备用。加适量水，配制成含水率为5%、10%、15%、20%的样本，土壤样品装入相同大小的容器（直径为30.08 mm，高度为 63.02 mm）内静置24 h保证土壤样品的均匀性。

2.2试验方法

本研究采用数字电桥测量仪（TH2828S高频LCR数字电桥）测量土壤相对介电常数特性。将直径为36.05 mm的铜制探头与样品表面紧密接触，设定相同电压、相同受力，为避免外界干扰，样品在屏蔽箱内进行测量。以测试频率、含水率、温度和容重为试验因素，以电容为考核指标。在同一测量频率下，测量土壤样品电容随含水率、温度、容重增大的变化规律，测量6组，取平均值。最后计算出相对介电常数。测量后的土壤样品，用天平（FA1004）称质量并记录，然后用烘干法（电热鼓风干燥箱，型号GZX-9140MBE）测量其含水率[18]。

介质材料的介电常数一般采用相对介电常数εr来表示，表征介质材料的介電性质或极化性质的物理参数，通常采用测量样品的电容量，经过计算求出εr，它是一个无量纲数，因此单位是1，满足如下关系：

式中：ε为绝对介电常数；ε0为真空介电常数，ε0=8.85×10-12 F/m；S为样品的有效面积；h为样品的厚度；d为样品的直径；C为被测样品的电容量。本试验中，样品的直径、高度均用游标卡尺测量（测量6次），直径平均值为30.08 mm，高度平均值为63.02 mm。

2.3数据处理方法

数据采用Excel和SPSS进行处理和分析，采用多元线性回归比较各因素的权重。

3结果与分析

3.1线性回归变量选取

为了充分了解含水率、温度和容重与对应的土壤介电常数的权重大小，根据相对介电系数的试验实测数据，选取土壤的相对介电常数y为预测目标（因变量），含水率x1、温度x2、容重x3作为预测因子（自变量）。

3.2线性回归分析过程

回归分析的主要任务是探寻各项预测因子之间的相互关系及对于预测目标贡献值的大小，采用多元回归法对预测量y与预报因子xk之间的关系进行分析。本研究是根据土壤的相对介电常数y与含水率x1、温度x2、容重x3的测量值来解决以下几个问题：（1）通过将测量值带入回归方程，确定常数项及待定参数的值，并给出回归方程。（2）对回归方程进行回归标准差、相关系数检验，以验证自变量与因变量之间是否高度正相关，以确定方程是否可以用于预测土壤相对介电常数。（3）在方程可以用于预测条件下，利用回归方程对因变量进行预测。

3.3相关性结果分析

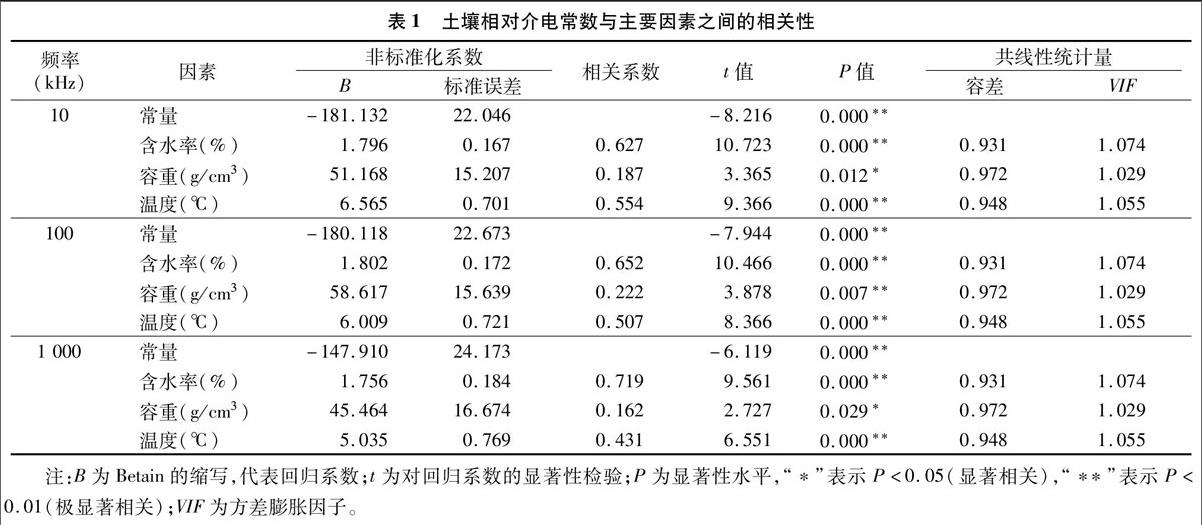
由表1可知，在频率为10、100、1 000 kHz测试条件下，3个变量中容重对土壤相对介电常数的影响程度最大，其次是温度，而含水率的影响最小。从显著性水平的P值也可以看出模型整体的拟合效果较好，含水率、容重、温度与土壤相对介电常数显著相关（P<0.05），其中含水率、温度与土壤相对介电常数极显著相关（P<0.01）。考虑到含水率、容重、温度与土壤介电常数显著相关，因此对含水率、容重、温度做基于土壤相对介电常数的多元线性回归预测，预测模型中自变量的容差在0.931～0.972之间，VIF值在1.029～1.074 之间，接近于1，表示回归方程式的自变量之间多元共线性非常弱，回归方程可以选择含水率、容重、温度为预测因子。

3.4线性回归结果分析

由表2可知，在频率为10、100、1 000 kHz测试条件下，以土壤的相对介电常数y为预测目标（因变量），含水率x1、温度x2、容重x3作为预测因子（自变量）的多元线性回归方程相似，显著性指标P=0.000，即回归模型方程皆达到极显著水平（P<0.01），相关系数r均大于0.970，显著性检验系数F值均大于38.700，多元线性回归方程拟合效果较好。

3.5不同频率下的直方图与标准残差P-P图分析

图1至图3分别为10、100、1 000 kHz频率下的直方图与标准残差P-P图。回归标准化残差的直方图表明了数据的正态性；回归标准化残差的标准P-P图中，各观测的散点基本呈直线趋势，散点基本上都分布在对角线上，可以判断残差服从正态分布，说明该方程有意义。

4结论与讨论

土壤作为一种代表性的电介质材料，它的基础物理参数表2土壤相对介电常数多元线性回归

频率（kHz）多元线性回归方程RF值P值

包括土壤容重、土壤温度、土壤含水率等相关参数[19-20]。本研究利用SPSS软件的统计分析功能对土壤相对介电常数进行了多元线性回归分析，得到了如下结论：在测试频率一定的条件下，土壤的相对介电常数作为预测目标与含水率、温度和容重预测因子之间的规律可用多元线性回归模型进行拟合；通过检验得出r均大于0.970，预测目标与预测因子之间高度正相关，说明本研究采用的多元线性回归模型具有很好的实际应用价值；从预测的多元线性回归方程可以看出，在不同测试频率下，影响土壤的相对介电常数的3个预测因子中，权重的大小顺序始终为容重>温度>含水率。

参考文献：

[1]邹维. 土和土壤的工程名称与分类及使用区别[J]. 水土保持应用技术，2010（2）：26-27.

[2]潘金梅，张立新，吴浩然，等. 土壤有机质对土壤介电常数的影响[J]. 遥感学报，2012，16（1）：13-24.

[3]Topp G C，Davis J L，Annan A P. Electromagnetic determination of soil water content：measurements in coaxial transmission lines[J].

Water Resources Research，1980，16（3）：574-582.

[4]Jackson T J，Schmugge J，Engman E T. Remote sensing applications to hydrology：soil moisture[J]. Hydrological Sciences Journal，1996，41（4）：609-624.

[5]康学远，林琳，刘义佳，等. 土壤介电常数-含水量关系模型研究[J]. 中国农村水利水电，2015（8）：8-12.

[6]朱安宁，吉丽青，张佳宝，等. 不同类型土壤介电常数与体积含水量经验关系研究[J]. 土壤学报，2011，48（2）：263-268.

[7]Velázquez-Martí B，Gracia-López C，Plaza-Gonzalez P J. Determination of dielectric properties of agricultural soil[J]. Biosystems Engineering，2005，91（1）：119-125.

[8]雷磊，塔西甫拉提·特依拜，丁建丽，等. 干旱区盐渍土介电常数特性研究与模型验证[J]. 农业工程学报，2013，29（16）：125-133.

[9]司马文霞，艾琳丰，袁涛，等. 土壤介电频变特性试验研究及其对接地极冲击特性的影响[J]. 中国电机工程学报，2015，35（16）：4247-4253.

[10]張鹏. 主要因素对土壤介电特性的影响分析研究[D]. 杨凌：西北农林科技大学，2013.

[11]郭文川，张鹏，宋克鑫，等. 土介电特性与水分检测频率及温度影响[J]. 排灌机械工程学报，2013，31（8）：713-718.

[12]田兵. 多元线性回归分析及其实际应用[J]. 阴山学刊（自然科学版），2011，25（1）：16-19.

[13]Shang J Q，Scholte J W，Rowe R K. Multiple linear regression of complex permittivity of a till at frequency range from 200 MHz to 400 MHz[J]. Sensing and Imaging，2000，1（3）：337-356.

[14]Shi T Z，Cui L J，Wang J J，et al. Comparison of multivariate methods for estimating soil total nitrogen；with visible/near-infrared spectroscopy[J]. Plant and Soil，2013，366（1）：363-375.

[15]Bilgili M. Prediction of soil temperature using regression and artificial neural network models[J]. Meteorology and Atmospheric Physics，2010，110（1）：59-70.

[16]周晨，冯宇东，肖匡心，等. 基于多元线性回归模型的东北地区需水量分析[J]. 数学的实践与认识，2014，44（1）：118-123.

[17]黄安，杨联安，杜挺，等. 基于多元成土因素的土壤有机质空间分布分析[J]. 干旱区地理（汉文版），2015，38（5）：994-1003.

[18]鲍士旦. 土壤农化分析[M]. 3版. 北京：中国农业出版社，2000.

[19]黄昌勇. 土壤学[M]. 北京：中国农业出版社，2000.

[20]Schmugge T J，Jackson T J，Mckim H L. Survey of methods for soil moisture determination[J]. Water Resources Research，1980，16（6）：961-979.