基于无向图所有生成树的网络重构遗传算法

张 剑，何怡刚

（合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

0 引言

为了提高供电可靠性，城市配电网一般设计为环网结构，为了减小短路电流以及便于继电保护的整定，一般采用开环运行方式。配电线路中包含大量常闭的分段开关及少量常开的联络开关。配电网网络重构通过调整开关状态能够达到降低网损、隔离故障、均衡负荷、提高电压等目的。目前，配电网自动化示范工程在全国各大中城市全面铺开，配电网自动化系统能够人工、交互或者自动地调整开关状态，为网络重构的实际工程应用奠定了良好基础。

配电网网络重构是一种大规模、非线性组合优化问题，主要有支路交换法［1-3］、最优流法［4］、遗传算法［5-14］、启发式方法［15-18］、混合方法［19］等。由于遗传算法具有不依赖于初值、鲁棒性好、能得到全局最优解等优点，得到了众多学者的关注。

在最初的基于遗传算法的配电网网络重构中，通常采用二进制编码方法，每个开关对应染色体中的一个基因位，基因为0表示开关打开，为1表示开关闭合。这种编码方式容易理解、实现简单。但是大量不能打开的开关也参与了编码，导致染色体较长，在交叉、变异过程中会产生大量不可行解，程序搜索效率十分低下。

文献［7］提出了一种只对环路中的开关进行二进制编码，对交叉、变异后产生的不可行解进行改良操作的网络重构遗传算法，该方法缩短了染色体长度，但初始种群中含有大量不可行解，改良过程需要耗费大量时间。文献［8］提出了构成同一环路的开关在同一基因块内、相邻开关在染色体中相邻的二进制编码策略，交叉操作为单个基因块内开关的交换，变异操作只能针对单个开关，而且变异过程产生不可行解，修正操作耗费时间，效率较低。文献［9］提出了基于环路的十进制编码方法，缩短了编码长度，在有开关处于多个环路时仍然会产生大量不可行解。

本文提出了一种基于无向图所有生成树的配电网网络重构遗传算法，该方法首先将配电网拓扑结构图中所有联络开关闭合，形成环状图，然后将不在环路中的支路去掉，并将度为2的相邻节点所在的支路合并为一条边，得到配电网拓扑简化无向图，然后搜索出简化无向图的所有生成树。简化无向图减去生成树得到连支，连支的每条边上有且仅有一个开关打开，其余开关闭合，具体打开哪个开关将由遗传算法搜索得出。提出了以连支的边上开关数量为基向量、开关在边上的编号为优化变量的十进制编码方法，大幅缩短了编码长度；每棵生成树对应一个子种群，选择、交叉、变异、重插入等遗传操作都在子种群中进行，得到的子代个体自动满足配电网辐射状、无孤岛的运行约束条件，不需要进行任何附加的改良操作，避免了传统遗传算法产生大量不可行解的弊端，提高了搜索效率；并行计算各个子种群的遗传操作，大幅提高了计算速度；根据指定的进化代数，目标函数值最小的染色体对应的打开开关即为问题的全局最优解。

本文提出的方法无论在产生初始种群还是遗传操作，都没有不可行解产生，而且由于采用了并行计算方法，大幅提高了程序的计算速度。算例表明，本文提出的方法极大地提高了搜索效率。

1 网络重构的数学模型

本算法的目标是网络重构后网损最小，且满足配电网运行必要的约束条件。目标函数为：

其中，Pi、Qi分别为支路i末端流过的有功、无功功率；Ui为支路i末端的节点电压；n为支路数；ri为支路i的电阻；ki为支路i上的开关状态，是0-1离散变量，0表示打开，1表示闭合；f为网络有功损耗，可以通过潮流计算得到。

节点电压与支路功率应满足以下约束条件。

a.节点电压约束：

其中，Uimax、Uimin分别为节点i电压有效值的上、下限。

b.支路功率约束：

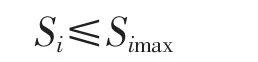
其中，Si、Simax分别为支路i上流过功率的计算值、允许的最大值。

当电压及支路功率出现越限时，计算越限比例并将其计入罚函数中，越限越多，罚函数越大，然后将罚函数计入目标函数中。

2 简化图的所有生成树及相关概念

2.1 简化图的生成树与连支

城市配电网拓扑结构图是以配变或线路为支路、负荷母线为节点的有环、无向、连通图。将不在环路中的支路去掉，并将度为2的相邻节点所在的支路合并成一条边，由此构成一个简化图G。G的生成树是G的一个子图，其中任意2个节点之间有且仅有一条简单路径。生成树包含G的所有节点，但不包含G的所有边，不同的生成树由不同的边组成。G减去生成树剩下的边组成的集合称为连支，一个连支包含的边数等于环数，采用无向图所有生成树的搜索算法［20-21］可以搜索出简化图的所有生成树及其连支，本文采用文献［20］的方法。

图1为IEEE典型的三馈线试验系统，虚线为联络开关所在支路，将图1中的母线1、2、3连接起来，去掉不在环路中的支路，并将度为2的相邻节点所在的支路合并为一条边，可以简化为图2所示的形式。由图2 可以清晰地看出，边（1）、（3）、（4）、（5）构成配电网简化图的一棵生成树，边（2）、（6）、（7）为该生成树的连支；边（1）、（2）、（4）、（5）构成另一棵生成树，边（3）、（6）、（7）为该生成树的连支。

图2的所有生成树及其对应的连支分别如表1的第2、3列所示。

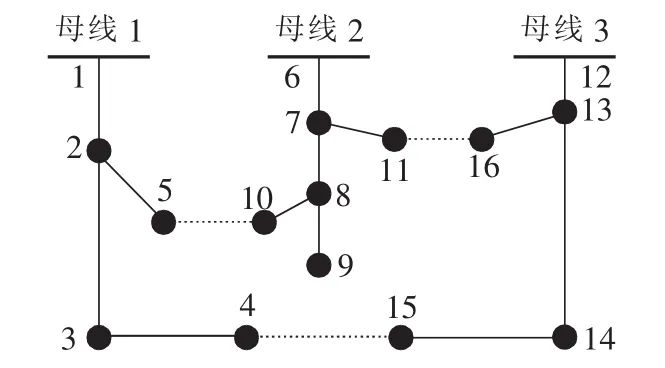
图1 IEEE典型的三馈线试验系统Fig.1 Typical IEEE three-feeder test system

图2 简化系统Fig.2 Simplified system

表1 生成树、连支及基向量Table 1 Spanning tree，connecting branch and base vector

2.2 连支的基向量

连支的基向量为以连支中每条边上的开关数量组成的向量。如表1第2行所示，连支1由边（1）、（2）、（4）组成，边（1）上的开关数量为1，边（2）上的开关数量为5，边（4）上的开关数量为1，因此连支1的基向量为（1 5 1）。图2的所有连支对应的基向量如表1第4列所示。

2.3 候选解

配电网任意满足辐射状、无孤岛约束条件的打开开关组合对应网络重构的一个可行解，这个可行解即为候选解。最优解只能从候选解中产生。当且仅当从连支的每条边中选择一个开关打开，产生一个候选解。将连支基向量的每个分量作乘积运算即可得到连支对应的候选解数目。将每个连支对应的候选解数量累加即可得到整个配电网网络重构总的候选解数目。如表1第2行第5列所示，生成树1的候选解数目为1×5×1=5。即在连支1上能够打开的满足辐射状、无孤岛约束条件的开关组合共有5种。如表1第26行第5列所示，IEEE典型的三馈线试验系统候选解的数目为190个。

3 编码方案与遗传操作

3.1 编码方案

遗传算法的任务是通过寻优确定连支及该连支每条边上打开开关的编号。本文采用十进制编码方法，子种群与连支一一对应，子种群中染色体的长度等于连支上边的个数，亦等于配电网拓扑结构图的网孔数，相比于传统的二进制编码方法，染色体长度大幅缩短。染色体每一位的取值等于对应边上打开开关的编号，为小于基向量对应位的非负整数。染色体第i位取 0、1、2、…、Ni-1 中的某一个值，Ni为连支第i条边上的开关数目。染色体只有属于子种群才有意义，染色体的每一位数值大小相同，但是属于不同的子种群，其含义截然不同。如子种群1中的染色体为（0 0 0），其含义为打开连支1的边（1）上的第0号开关、边（2）上的第0号开关、边（4）上的第0号开关。子种群2中的染色体为（0 0 0），其含义为打开连支2的边（1）上的第0号开关、边（4）上的第0号开关、边（6）上的第0号开关。

3.2 产生初始种群

子种群的个数等于生成树的个数，子种群中染色体的个数可以根据子种群候选解个数的不同而不同。如子种群3的候选解的个数为15，因此染色体数目可以选取为2，子种群10的候选解的个数为45，因此染色体数目可以选取为6。对于每个子种群，可以根据候选解个数产生指定数目的染色体。

3.3 染色体的适应度值

对染色体代表的配电网中打开的开关进行解码，采用并行前推回代算法［22］计算网损值（单位为kW），对子种群中每个染色体对应的网损值按照从小到大进行排序，对序号从大到小等间隔线性映射为0～2中实数，即网损最大的染色体对应的适应度值为0，网损最小的染色体对应的适应度值为2，排序后序号相邻的染色体适应度值间隔相等。

3.4 基因操作

基因操作包括选择、交叉、变异、重新插入，都在子种群中进行，子种群的编码策略决定了基因操作不会产生不可行解。在完成了指定的进化代数后，整个种群（不是子种群）中目标函数值最小的个体就是最优解。

（1）选择。

对于每个子种群，根据适应度值，采用“赌轮盘”法选择N（N为偶数）个个体，进行遗传操作。

（2）交叉。

交叉操作方法为按照指定的概率将双亲染色体对应基因位数值互换。如指定交叉概率为0.7，表1中子种群10双亲染色体交叉后可能的结果如表2所示。

表2 交叉操作Table 2 Crossover operation

（3）变异。

变异操作为按照指定的变异概率将染色体中一位或多位基因替换为小于基向量对应位的非负整数值。如指定变异率为0.01，表1中子种群10的双亲染色体变异后的子代个体一种可能的结果见表3。

表3 变异操作Table 3 Mutation operation

（4）重新插入。

将每个子种群中选择的N个完成了交叉、变异操作的个体重新插入父代，同时淘汰子种群父代中适应度值最小的N个个体。由此，既保持了子种群个体数量恒定，又保留了子种群父代的多个适应度最大的个体，即精英保留，实现了“优胜劣汰”。

3.5 并行计算

编码、初始种群的产生、适应度值的计算、遗传操作都是在子种群中进行，子种群之间没有任何计算上的耦合关系，非常适合于并行计算。本文基于MATLAB/PARALLEL COMPUTING工具箱采用并行计算方法，大幅提高了算法的计算速度。

3.6 算法的逻辑框图

本文所提出的算法的总体框图如图3所示。输出结果时，选择种群中（非子种群）目标函数值最小的个体作为问题的最优解。

4 算例

图3 算法总体逻辑框图Fig.3 Flowchart of algorithm

本文采用2个算例进行了试算，分别用于验证单电源供电与多电源供电情况下所提算法的正确性与快速性，为了方便记录数据，在试验中采用前述方法确定最佳解，再以得到的最佳解作为程序终止的条件。程序采用MATLAB编写。

算例1：以3馈线16节点3网孔系统为例，如图1所示，正常情况下，该系统母线没有直接相连，在计算该配电网拓扑图的生成树时，可以将3条馈线的母线相连，简化为图2的形式，便于生成树的搜索。图2的生成树为24个，总的候选解为190个。子种群为24个，染色体长度为3，由于总的候选解数目较小，在生成初始种群时，每个子种群的染色体与该子种群候选解一一对应，应用穷举法直接找到全局最优解。

图4 美国PG&E 69节点配电系统Fig.4 American PG&E 69-bus distribution network

算例2：以美国PG&E 69节点配电系统为例，如图4所示，该系统含有69个节点、73条支路、5个网孔，其中节点1为电源节点，简化图的生成树为463个。

总的候选解为377417个，子种群数为463个，候选解最大的37个子种群染色体为4个，其他子种群染色体数为2个，总的染色体数目为1000个，染色体长度为5，交叉率pc=0.7，变异率pm=0.01，运算50次。

算例1和2的重构结果和相关统计如表4、5所示。

对于16节点系统，直接找到全局最优解，所需时间为0.012 s。对于69节点系统，找到最优解的平均进化代数为6代，6代的平均计算时间为0.534 s，远优于文献［8］的结果。本文程序搜索出最佳解的进化代数之所以远小于文献［8］是因为总的染色体数是文献［8］的10倍；计算时间远比文献［8］短是因为染色体长度约为文献［8］的1/12，不产生不可行解，不需要改良操作，采用了并行计算方法；本文结果与文献［8］的优化结果不同是因为节点45、46、47上没有负荷，打开 44-45、45-46、46-47、47-48 开关的效果相同。

由上述算例可知，本文所提出的算法具有十分优越的搜索效率与计算速度。

表4 2个配电网的重构结果Table 4 Results of reconfiguration for two distribution networks

表5 进化统计Table 5 Statistics of evolution

5 结论

本文提出的基于无向图所有生成树的配电网网络重构遗传算法，能够精确计算出候选解的总的数目及分布情况，能够为子种群数量、子种群中染色体数量提供参考数据；彻底克服了传统配电网网络重构遗传算法产生大量不可行解的弊端，提高了搜索效率；采用了十进制编码方法，大幅缩短了编码长度；采用并行计算方法，大幅缩短了计算时间；具有十分优越的应用价值。

值得指出的是，本文方法对于大规模配电网系统仍然适用。原因如下：本文针对配电网无向图的简化图而不是原图进行搜索，大幅节省了搜索时间；本文采用的搜索算法的时间复杂度正比于简化图的节点数乘以支路数，计算的复杂度较低，采用最新的搜索算法可以进一步降低时间复杂度，达到正比于支路数；本文的核心程序采用了递归调用技术，大幅提高了计算效率。

参考文献：

［1］何禹清，彭建春，文明，等.配电网重构的最小可行分析对象及其快速算法［J］.中国电机工程学报，2010，30（31）：50-56.HE Yuqing，PENG Jianchun，WEN Ming，et al.Minus feasible analysis unit and fast algorithm for distribution network reconfiguration［J］.Proceedings of the CSEE，2010，30（31）：50-56.

［2］吉兴全，刘琪，于永进.基于功率矩和邻域搜索的有源配电网两层重构算法［J］.电力自动化设备，2017，37（1）：28-34.JI Xingquan，LIU Qi，YU Yongjin.Two-level reconfiguration algorithm based on power moment and neighbourhood searching for distribution network［J］.Electric Power Automation Equipment，2017，37（1）：28-34.

［3］毕鹏翔，刘健，张文元.配电网络重构的改进支路交换法［J］.中国电机工程学报，2001，21（8）：98-103.BI Pengxiang，LIU Jian，ZHANG Wenyuan.A refined branch exchange algorithm for distribution network reconfiguration［J］.Proceedings of the CSEE，2001，21（8）：98-103.

［4］雷健生，邓佑满，张伯明.综合潮流模式及其在配电系统网络重构中的应用［J］.中国电机工程学报，2001，21（1）：57-62.LEIJiansheng，DENG Youman，ZHANG Boming.Hybridflow pattern and its application in network reconfiguration［J］.Proceedings of the CSEE，2001，21（1）：57-62.

［5］刘健，毕鹏翔，董海鹏.复杂配电网简化分析与优化［M］.北京：中国电力出版社，2002.

［6］毕鹏翔，刘健，张文元.配电网络重构的研究［J］.电力系统自动化，2001，25（14）：54-60.BI Pengxiang，LIU Jian，ZHANG Wenyuan.Study on algorithms of distribution network reconfiguretion［J］.Automation of Electric Power Systems，2001，25（14）：54-60.

［7］李晓明，黄彦浩，尹项根.基于改良策略的配电网重构遗传算法［J］.中国电机工程学报，2004，24（2）：49-54.LI Xiaoming，HUANG Yanhao，YIN Xianggen.A genetic algorithm based on improvement strategy for power distribution network reconfiguration［J］.Proceedings of the CSEE，2004，24（2）：49-54.

［8］毕鹏翔，刘健，刘春新，等.配电网络重构的改进遗传算法［J］.电力系统自动化，2002，26（2）：57-61.BI Pengxiang，LIU Jian，LIU Chunxin，et al.A refined genetic algorithm for power distribution network reconfiguration［J］.Automation of Electric Power Systems，2002，26（2）：57-61.

［9］麻秀范，张粒子.基于十进制编码的配网重构遗传算法［J］.电工技术学报，2004，19（10）：65-69.MA Xiufan，ZHANG Lizi.Distributionnetwork reconfiguration based on genetic algorithm using decimal encoding［J］.Transactions of China Electrotechnical Society，2004，19（10）：65-69.

［10］NARA K，SHIOSE A，KITAGAWA M，et al.Implementation of genetic algorithm for distribution system loss minimum reconfiguration［J］.IEEE Transactions on Power Systems，1992，7（3）：1044-1051.

［11］许奎.基于改进自适应遗传算法的配电网重构的研究［D］.南宁：广西大学，2008.XU Kui.A study of reconfiguration network based on improved adaptive genetic algorithms［D］.Nanning：Guangxi University，2008.

［12］王艳松，陈国明，张加胜，等.基于小生境遗传算法的配电网开关优化配置［J］.电工技术学报，2006，21（5）：82-86.WANG Yansong，CHEN Guoming，ZHANG Jiasheng，et al.Optimal switching device placement based on niche genetic algorithm in distribution networks［J］.Transactions of China Electrotechnical Society，2006，21（5）：82-86.

［13］刘莉，陈学允.基于模糊遗传算法的配电网络重构［J］.中国电机工程学报，2000，20（2）：66-69.LIU Li，CHEN Xueyun.Reconfiguration of distribution network based on fuzzy genetic algorithm［J］.Proceedings of the CSEE，2000，20（2）：66-69.

［14］余贻鑫，段刚.基于最短路算法和遗传算法的配电网络重构［J］.中国电机工程学报，2000，20（9）：44-49.YU Yixin，DUAN Gang.Shortest path algorithm and genetic algorithm based distribution system reconfiguration［J］.Proceedings of the CSEE，2000，20（9）：44-49.

［15］葛少云，刘自发，余贻鑫.基于改进禁忌搜索的配电网重构［J］.电网技术，2004，28（23）：22-26.GE Shaoyun，LIU Zifa，YU Yixin.An improved Tabu search for reconfiguration of distribution systems［J］.Power System Technology，2004，28（23）：22-26.

［16］王守相，王成山.一种隐含并行的大规模三相不平衡配电网络重构新算法［J］.电力系统自动化，2000，24（10）：34-38.WANG Shouxiang，WANG Chengshan.A novel network reconfiguration algorithm implicity including parallel searching for large scale unbalanced distribution systems［J］.Automation of Electric Power Systems，2000，24（10）：34-38.

［17］TALESKI K，RAJICID D.Distribution network reconfiguration for energy loss reduction［J］.IEEE Transactions on Power Systems，1997，12（1）：398-406.

［18］陈根军，李继洸，唐国庆.基于Tabu搜索的配电网络配电网重构算法［J］.中国电机工程学报，2002，22（10）：28-33.CHEN Genjun，LI Jiguang，TANG Guoqing.A Tabu search approach to distribution network reconfiguration for loss reduction［J］.Proceedings of the CSEE，2002，22（10）：28-33.

［19］刘蔚，韩祯祥.基于最优流法和遗传算法的配电网重构［J］.电网技术，2004，28（19）：29-33.LIU Wei，HAN Zhenxiang.Distribution network reconfiguration based on optimal flow pattern algorithm and genetic algorithm［J］.Power System Technology，2004，28（19）：29-33.

［20］HAROLD N G，EUGENE W M.Finding all spanning trees of directed and undirected graphs［J］.Society for Industrial and Applied Mathematics，1978，7（3）：280-287.

［21］杨元生.无向图与有向图的全部生成树的计算机算法［J］.计算机学报，1983（2）：152-154.YANG Yuansheng.A computerized algorithm for finding all spanning trees of directed and undirected graphs［J］.Chinese Journal of Computers，1983（2）：152-154.

［22］颜伟，刘芳，王官洁，等.辐射型网络潮流的分层前推回代算法［J］.中国电机工程学报，2003，23（8）：76-80.YAN Wei，LIU Fang，WANG Guanjie，etal.Layer-by-layer back /forward sweep method for radial distribution load flow［J］.Proceedings of the CSEE，2003，23（8）：76-80.