基于安全域的大规模风电并网系统低频振荡稳定分析

秦 超，曾 沅，苏寅生，李 鹏

（1.天津大学 智能电网教育部重点实验室，天津 300072；2.中国南方电网电力调度控制中心，广东 广州 510623）

0 引言

能源危机与环境污染迫使人类寻求清洁的可再生能源。作为目前公认的最具开发潜力并且技术发展最为成熟的可再生能源发电形式之一，风电在世界范围内得到了广泛的开发与利用［1］。双馈风机DFIG（Doubly-Fed Induction Generator）是目前大型风电场广泛采用的主流机型之一，具有效率高、控制灵活等诸多优点［2］。

低频振荡是现代互联电网面临的关键性挑战之一，严重威胁着电网的安全稳定运行［3］。风电的多变性、间歇性等特性，势必使电网的运行状态更加复杂多变，对电力系统的安全稳定运行带来了诸多挑战［4-5］。需要说明的是，我国风电大规模集中并网、远距离外送的特殊发展实践使得风电并网后的低频振荡问题更为严峻［6-7］。

低频振荡属于电力系统小扰动稳定性的研究范畴［8］，为此，国内外学者已围绕风电并网对电力系统小扰动稳定的影响开展了广泛的研究［9］。然而，已有研究多以特征值分析［10-11］、频域分析［12-13］或时域仿真［14-15］等为手段，针对某些风电并网后的典型运行场景，分析系统的低频振荡特性；在此基础上，通过对有些关键变量进行扰动分析，以确定风电接入对电力系统小扰动稳定性的影响。这类方法都属于“逐点法”的范畴，其缺陷在于：所得结论严格与系统的运行状态相关，一旦系统的运行状态（如发电方式、负荷水平等）改变需要重新计算，难以对电力系统的安全性与稳定性进行整体评价；只能给出系统是否安全、稳定的二元信息，难以度量系统的稳定裕度，即当前运行点到稳定边界的距离以及稳定储备的大小等。大规模风电并网后，电力系统的运行方式更加复杂多变，若借助“逐点法”对系统所有可能的运行方式逐一进行小扰动稳定性分析是不现实的。

安全域的方法从系统安全稳定运行的整体出发，可以给出系统的安全裕度、最优控制方向等丰富信息，并且它是由系统的网络拓扑决定的，不随运行点的改变而变化，因此，可有效克服“逐点法”的缺陷，已得到电网研究人员越来越多的关注［16］。

本文研究的是节点注入空间上保证系统小扰动稳定的安全域，即小扰动稳定域SSSR（Small Signal Stability Region）。在相关领域，国内外学者已围绕SSSR的构建方法、边界性质等方面开展了广泛的研究［17-21］。随着风电并网规模的增加，已有文献围绕风电接入系统的SSSR展开了研究：文献［22］分析了DFIG接入后，系统中主要机电振荡模态与SSSR边界的对应关系，并提出了用超平面拟合注入功率空间上含DFIG电力系统的SSSR边界的建议；文献［23］分析了DFIG接入单机无穷大系统时，系统SSSR的变化。

针对大规模风电并网系统，本文以SSSR的方法为基础，分析了双馈风电场替换同步机前后，系统可保持小扰动稳定的运行区域的变化及其机理；进而研究了输电距离、DFIG有功控制回路和无功控制回路PI参数对含大规模风电互联电网低频振荡稳定性的影响。

1 DFIG模型

双馈风力发电系统的模型一般包括风轮机模型、发电机模型、变流器模型、桨距角控制模型和轴系模型等。

1.1 风轮机的功率特性

根据贝兹定律，风轮机的功率特性如式（1）所示。

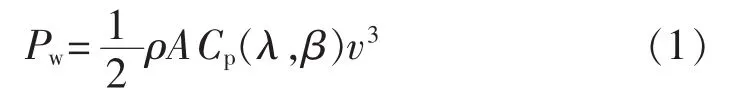
其中，Pw为风轮机捕捉到的风功率；A为风轮机的叶片扫风面积；v为风速；ρ为空气密度；λ为叶尖速比，即λ=ΩR/v，R为风轮机叶片的半径，Ω为风轮机转速；β为桨距角；Cp为风能转换系数，是叶尖速比和桨距角的函数。

1.2 发电机模型

在采用发电机定子电压定向的同步旋转dq坐标系下，DFIG系统的发电机方程如式（2）—（5）所示。

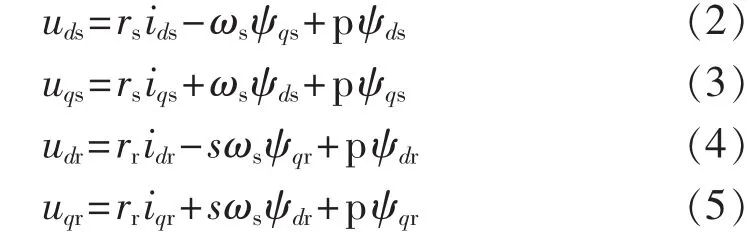
其中，uds、udr和 uqs、uqr分别为发电机定、转子电压d轴和q轴分量；ids、idr和 iqs、iqr分别为发电机定、转子电流d轴和q轴分量；rs和rr分别为发电机定、转子电阻；ψds、ψdr和ψqs、ψqr分别为发电机定、转子磁链d轴和q轴分量；s为发电机转差；ωs为同步转速；p为微分算子。

1.3 变流器模型

机侧变流器的控制结构如图1所示。图中，Pref和Qref分别为有功和无功功率参考值；P和Q分别为实际有功和无功输出。

图1 机侧变流器控制框图Fig.1 Block diagram of generator-side converter control

网侧变流器的控制结构如图2所示。图中，Udcref和Udc分别为直流电容电压参考值与实际值；Qgref和Qg分别为网侧变流器发出无功功率的参考值与实际值；udg和uqg分别为网侧变流器输出电压的d轴和q轴分量；idg和iqg分别为网侧变流器电流的d轴和q轴分量。

图2 网侧变流器控制框图Fig.2 Block diagram of grid-side converter control

1.4 桨距角控制回路模型

当代大型DFIG一般采取桨距控制，可用式（6）所示方程来表示桨距角控制回路的动态特性。

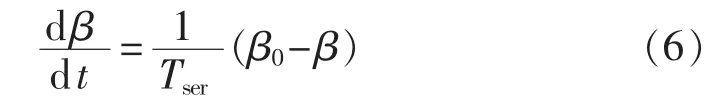
其中，Tser为惯性时间常数；β0为桨距角参考值。

1.5 轴系模型

DFIG发电系统的轴系通常可由如式（7）—（9）所示的双质量块模型来表示。

其中，ωt和ωg分别为风力机和DFIG的角速度；Ht和Hg分别为风力机和DFIG的惯性时间常数；θs为轴系扭转角；Ks和D分别为轴刚度系数和阻尼系数；Tm为风力机机械转矩；Te为发电机的电磁转矩。

2 电力系统SSSR

2.1 定义

电力系统的动态过程一般可以描述为如式（10）所示的微分代数方程组：

其中，x、y和p分别为电力系统的状态变量空间、代数变量空间和参数变量空间；f和g分别用来描述电力系统的微分方程和代数方程。

在平衡点（f0，g0，p0）处，将式（10）所示方程组线性化，可得：

在非奇异的前提下，由隐函数定理对式（11）整理得：

根据小扰动稳定性分析的特征值理论，当J（p）的所有特征值均具有负实部时，系统是小扰动稳定的。

电力系统的SSSR是指能够使系统保持小扰动稳定的系统稳态运行点的集合［17］，它既可以定义在参数空间上，又可以定义在节点注入空间上。本文研究的SSSR是定义在节点有功注入空间上的，如式（14）所示。

其中，p为电力系统节点功率注入向量；o2k表示考虑发电机输出限值的节点注入空间；R2k表示2k维实数空间；k为电力系统拓扑i中注入功率的节点个数；ΩSSSR（i）是由系统的网络拓扑i唯一确定的。

文中的小扰动主要是指系统中小的负荷扰动、发电扰动、风电出力变化等。当前，通常认为电力系统SSSR的边界主要由鞍节分岔、Hopf分岔和奇异诱导分岔3类局部分岔点构成［21］。

2.2 计算方法

为保障SSSR边界的计算精度，本文采用拟合法进行求解。具体步骤如下。

（1）选取系统中的n条母线（包括发电机母线和负荷母线）的有功注入构成安全域的参数空间X=［x1，x2，… ，xn］，将满足小扰动稳定约束的某一运行点作为初始搜索点Pstart。

（2）构建基本搜索点集合S0，确定可能的搜索方向。

a.确定n条母线有功注入上下限所构成的实用可行搜索范围W。

b.2维空间（即n=2）上集合S0的确定方法为：求解W的边界和特定射线i（以初始搜索点Pstart为起点，与纵轴夹角为θ=iΔθ，其中 i=0，1，2，… ，并且满足 iΔθ＜ 360°）的交点 Psi；所有 Psi即构成了集合 S0。

c.对于3维空间，可在立方体W的各轴上等间距选取m个点，由这些点构成集合S0。

d.对于n（n＞3）维空间，若通过类似2维空间的方法，枚举特定射线方向来确定基本搜索点意味着巨大的工作量，可借助Hadamard矩阵采取拟正交选点的方法来确定可能的射线方向，以降低工作量，并尽可能覆盖n维空间中所有的搜索方向，分别求取所有射线方向与W的交点构成集合S0。

（3）分别对步骤（2）所形成的基本搜索点 S0中的每一个运行点进行潮流计算与特征值分析，判断其是否满足小扰动稳定约束，将S0中所有不满足小扰动稳定约束的运行点构成集合SU。

（4）分别沿初始搜索点Pstart和集合SU中的每一个点间的连线，借助二分法进行临界点搜索。

a.设置。

b.计算PLeft和PRight的中点，作为下一个搜索点Psearch。

c.对Psearch进行潮流计算与特征值分析，以判断其稳定性，计算PLeft与PRight间的距离Dc。

d.若 Psearch满足小扰动稳定约束，并且 Dc＜dc，即满足收敛条件，则Psearch即为一个临界稳定点；若Psearch满足小扰动稳定约束，并且 Dc＞dc，则 PLeft=Psearch，返回步骤b；若Psearch不满足小扰动稳定约束，则Pright=Psearch，返回步骤 b。

e.判断是否已完成SU中所有点的搜索，若完成，则转入下一步；否则，i=i+1，返回步骤a。经过步骤d搜索得到的临界稳定点构成了基本临界点集合CPb。

（5）对步骤（4）中搜索得到的每个基本临界点进行扩展搜索，即以基本临界点为起点，在其邻域内进行扰动，搜索新的临界点。对于基本临界点的扩展搜索过程具体如下。

a.按照Hadamard确定扰动方向，对进行扰动，获得一个新的搜索点Pnew。

b.对Pnew进行潮流计算与特征值分析，以判断其是否满足小扰动稳定约束。

c.若Pnew小扰动稳定，则设置PLeft=Pnew，并将PRight设置为所对应的；若Pnew小扰动不稳定，则设置 PLeft=Pstart，PRight=Pnew。

d.计算PLeft和PRight的中点，作为下一个搜索点Psearch。

e.对Psearch进行潮流计算与特征值分析，以判断其稳定性，计算PLeft与PRight间的距离Dc。

f.若 Psearch小扰动稳定，并且 Dc＜dc，即满足收敛条件，则Psearch即为一个临界稳定点；若Psearch小扰动稳定，并且 Dc＞dc，则 PLeft=Psearch，返回步骤 d；若 Psearch小扰动不稳定，则Pright=Psearch，返回步骤d。

g.判断是否已完成所有搜索方向的扩展搜索，若完成，则转入下一步；否则，j=j+1，返回步骤a。

（6）对搜索到的所有临界点进行拟合，获得SSSR的边界，可通过搜索步长、搜索临界点的个数等参数，来控制搜索的精度。

2.3 小扰动稳定约束下系统区域间功率传输极限

对于区域互联电网，借助SSSR可以方便求解系统在小扰动稳定约束下区域间的功率传输极限，具体模型如下所示。

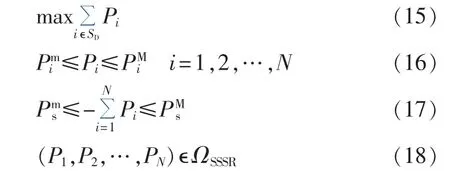
其中，SD为送端系统的节点编号集合；Pi为节点i的有功注入；和分别为节点i有功注入的下限和上限；和分别为平衡节点有功注入的下限和上限；N为系统中除平衡节点外的所有节点的总数。式（16）为各节点功率注入约束；式（17）为平衡节点的调节能力约束；式（18）为小扰动稳定约束。

在对该模型进行求解的过程中，参考文献［22］的方法，用超平面拟合SSSR的边界，从而式（18）所示的小扰动稳定约束可以进一步由式（19）所示的不等式描述。

其中，αi为SSSR边界的拟合系数。

3 算例分析

3.1 简介

本文采用一个两区域系统作为分析算例，其接线方式如图3所示。基于Digsilent软件实现系统的建模与特征值分析，并借助该软件提供的DPL语言实现了含双馈风电场电力系统的SSSR的计算程序。有关同步发电机、负荷、网架等的模型参数详见文献［8］。

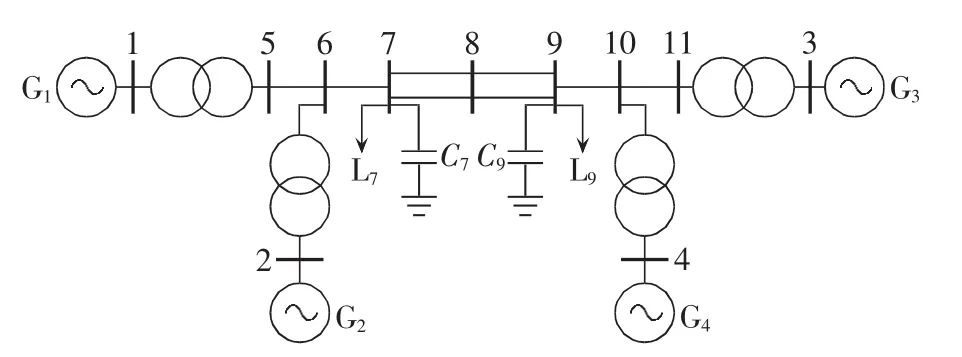
图3 两区域系统接线图Fig.3 Connection diagram of two-area system

本文考虑以下2种场景：场景A，不接入风电；场景B，采用同容量的DFIG替换同步发电机G1。其中，双馈风电场经过 0.69 kV/20 kV、20 kV/345 kV两级变压接入系统。

分别对上述2种场景的额定运行点（即同步机G1和风电场的有功出力均为700 MW）进行特征值分析，根据振荡频率和参与因子对所有振荡模态进行筛选，所得系统中主要的机电振荡模态见表1。由表可知，在场景A中存在3个主要的机电振荡模态；而在场景B中出现了1个不稳定的机电振荡模态。

表1 场景A和场景B中系统的主要低频振荡模态Table 1 Main low-frequency oscillation modes of Case A and Case B

3.2 DFIG接入前后，系统SSSR的变化

场景A和场景B所对应的SSSR如图4所示。其中，场景A的参数空间为G1和G2的有功出力；场景B的参数空间为DFIG和G2的有功出力。图中的矩形框表征了节点的允许注入范围；初始稳定点所在的一侧即为系统的SSSR。

3.2.1 仿真验证

为了验证所得SSSR的准确性，以场景B为例，在注入空间中选取若干运行点，分别借助SSSR方法和时域仿真方法对所选取运行点进行小扰动稳定校核。所选取的运行点及其与SSSR边界的相对位置如图5所示。

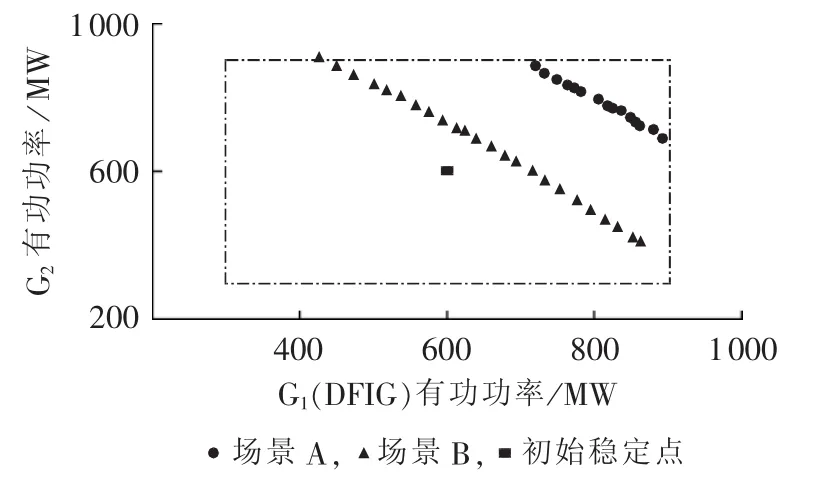
图4 场景A和场景B的SSSRFig.4 SSSR for Case A and Case B

图5 运行点及其与SSSR边界的相对位置（场景B）Fig.5 Operating points and SSSR boundary（Case B）

对于选定的运行点，向系统施加小扰动（在1.0 s时，母线7的负荷增加50%；经历0.01 s后，母线7的负荷恢复为初始值）进行时域仿真。图6给出了3个典型运行点（运行点a位于域内；运行点b位于域边界上；运行点c位于域外）在小扰动下的区域联络线上有功功率的时域仿真结果。由图6结果可知，在1.0 s系统受到扰动，区域联络线功率发生突变；此后，扰动消失后，运行点a所对应的区域联络线功率的振荡逐渐衰减，最终恢复至平稳运行状态；运行点b所对应的区域间联络线功率基本维持等幅振荡；而运行点c所对应的区域间联络线功率出现了增幅振荡。SSSR的分析结果与时域仿真方法一致，从而验证了本文计算所得SSSR的准确性。

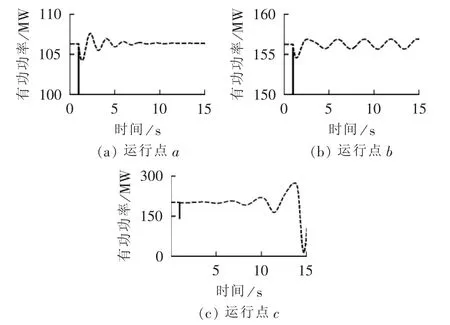
图6 时域仿真结果（场景B）Fig.6 Results of time-domain simulation（Case B）

3.2.2 机理分析

在同样的运行方式下，在1.0 s时对系统施加小扰动进行时域仿真，所得同步发电机G1和DFIG有功出力曲线如图7所示。

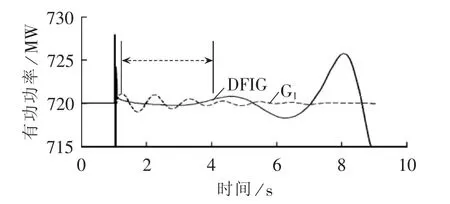
图7 小扰动下G1和DFIG的有功输出Fig.7 Active-power outputs of G1and DIFG under small disturbance

由图7结果可知，在1.0 s系统受到了扰动，同步机和DFIG的有功出力都出现了短暂的波动；在扰动消失后的一段时间内（1.1～4 s），同步机的有功出力发生了振荡，并且振荡幅值逐渐衰减，而DFIG输出的有功出力则基本上保持不变；此后，在4～10s内，同步机的有功出力逐渐恢复至平稳状态，而DFIG的有功出力则发生了增幅振荡。

在扰动消失系统恢复过程中，同步机和DFIG具有不同的功率特性，究其原因就在于DFIG采用与同步机完全不同的基于电力电子装置的交流励磁。无论是同步发电机还是DFIG采用的绕线式异步发电机，其有功输出均与发电机内电势幅值、端电压幅值及两者间的夹角相关。区别在于同步发电机的励磁回路通过调整励磁电流的幅值来改变发电机内电势幅值，其相位与转子位置严格相关，而DFIG由于采取了基于变流器的交流励磁，其励磁回路可灵活地调整励磁电流的幅值、相位和频率，其内电势的相角不再严格受转子位置限制。在扰动发生时，端电压及其与同步发电机内电势间的夹角发生变化，进而引起同步发电机输出电力功率的变化，在原动机输入功率不变的情况下，同步发电机转速随之变化，通过发电机转子吸收或释放部分动能来实现阻尼系统振荡的作用；而对于DFIG，在扰动下，一旦引起发电机有功输出发生变化，偏离控制回路的有功参考值，基于变流器的励磁回路会迅速调整励磁电流的幅值、相位和频率，从而使DFIG的有功输出基本维持恒定，从系统的角度看，这意味着DFIG并未消除系统功率振荡提供阻尼或者贡献很小，因此，用DFIG替换系统内的同步发电机后，在同样的运行方式下，系统的阻尼水平有所恶化；从域的角度看，DFIG的接入使得系统的SSSR有所缩小。

3.3 输电距离的影响

本文中所采用的算例为研究电力系统小扰动稳定性的经典算例，文献［8］中给出了该算例的详细数据，其中系统的输电距离为220 km。本文为了研究输电距离变化时系统SSSR的变化，对输电距离分别为原始算例中输电距离的50%、1.0倍、1.5倍和2倍4种场景进行分析。图8给出了风电接入系统后，在输电距离分别为110 km、220 km、330 km、440 km情况下系统的SSSR。借助2.3节所介绍的模型，分别对4种不同输电距离场景计算小扰动稳定约束下区域间功率传输极限，所得结果依次为609 MW、368 MW、233 MW和156 MW。结合图8结果可知，输电距离对大规模风电并网系统的低频振荡稳定具有显著影响；随着输电距离的增加，系统的SSSR显著变小。

图8 不同输电距离下系统的SSSRFig.8 SSSR for different transmission distances

3.4 DFIG控制参数的影响

由3.2节中的机理分析可知，DFIG转子励磁回路是决定其对系统低频振荡稳定特性影响的关键因素。而DFIG转子励磁回路动态特性在很大程度上依赖于控制回路的PI参数。DFIG的转子侧一般采取PQ解耦控制，因此存在有功控制回路和无功控制回路2套相对独立的控制回路。为此，本文参考Digsilent/PowerFactory软件提供的用于稳定性研究的DFIG示例，分别针对DFIG的有功控制回路和无功控制回路采取如下4种PI参数计算系统的SSSR：大比例大积分、小比例大积分、大比例小积分、小比例小积分。其中，小比例系数取值为2，大比例系数取值为4，小积分系数取值为1，大积分系数取值为20。

DFIG有功控制回路采取不同PI参数时，系统的SSSR如图9所示；同时，计算得到DFIG有功控制回路采用上述4种PI参数时，系统的区域间功率传输极限依次为368 MW、378 MW、468 MW和606 MW。图10给出了DFIG无功控制回路采取不同PI参数时，系统的SSSR；同时，DFIG无功控制回路采取上述4种PI参数时，系统的区域间功率传输极限依次为368 MW、375 MW、462 MW和551 MW。

由图9和图10结果可知，在大规模风电远距离外送场景下，DFIG变流器的控制参数对于电网的SSSR具有显著影响。有功控制回路和无功控制回路的PI参数对系统低频振荡的影响具有类似的规律：比较而言，积分系数对于系统的低频振荡特性的影响更为显著，在积分系数较大时，比例系数的影响很小；较小的比例系数与积分系数更有利于改善系统的低频振荡稳定特性；尽管从风机自身的控制特性考虑，较大的比例系数和较大的积分系数可保障较好的功率跟踪特性，却会显著恶化系统的低频振荡特性。

针对场景B，以系统的SSSR最大为目标，综合调整DFIG的有功和无功控制回路PI参数，所得到的系统SSSR如图11所示。

图9 有功控制回路采用不同PI参数时系统的SSSRFig.9 SSSR for different PI parameters of active-power control loop

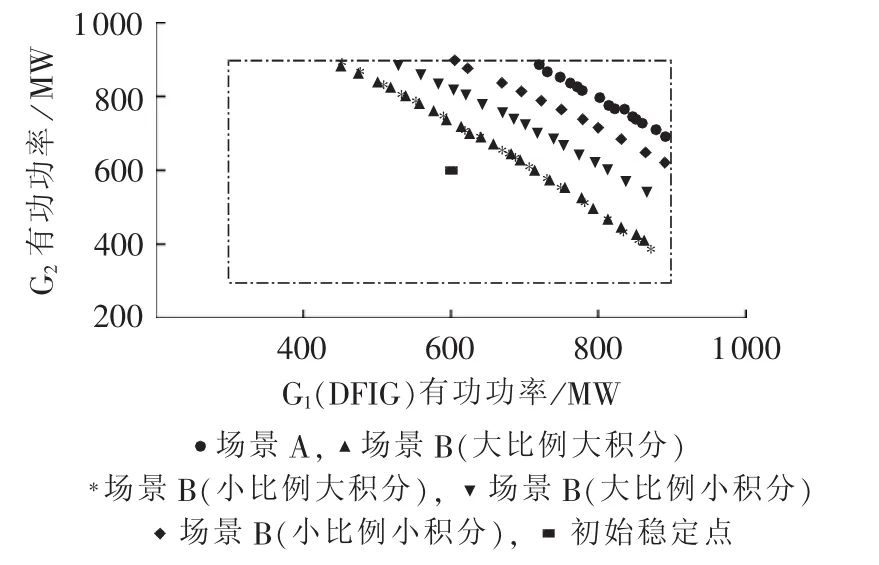
图10 无功控制回路采取不同PI参数时系统的SSSRFig.10 SSSR for different PI parameters of reactive-power control loop

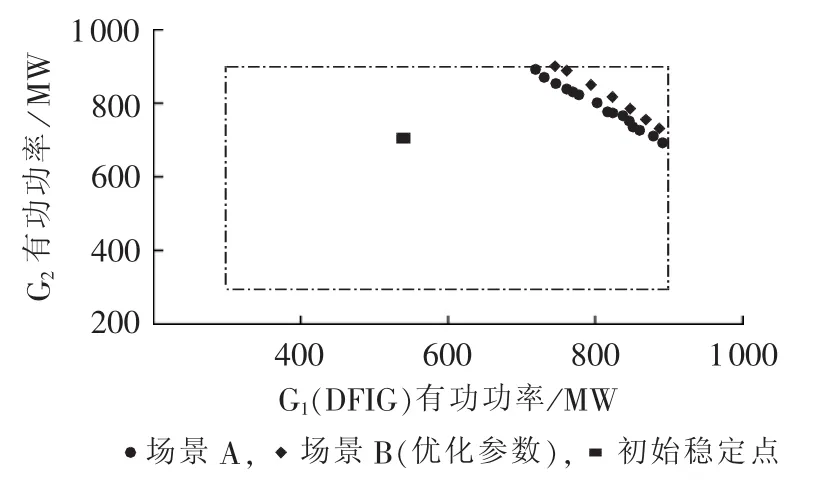
图11 场景A和场景B的SSSRFig.11 SSSR for Case A and Case B

由图11结果可知，通过合理地整定DFIG的PI参数，可降低DFIG接入对系统低频振荡的不利影响，甚至可扩大系统的SSSR。因此，从系统整体安全稳定运行的角度，大型风电场并网时，需综合考虑风电场接入电网的特性，合理设定变流器控制参数，以降低引发系统低频振荡的风险。

4 结论

本文计算了双馈风电场并网后系统的SSSR，对比分析了风电场接入前后系统SSSR的变化，借助时域仿真探索了SSSR的变化机理。结果表明，双馈风电场并网后会对系统的低频振荡特性产生显著影响，其影响的大小与输电距离和DFIG励磁回路控制参数相关；DFIG励磁控制回路采用较大的比例系数和积分系数时会显著恶化系统的小扰动稳定特性，而采用较小的比例系数和积分系数时可以降低系统发生低频振荡的风险。因此，建议借助SSSR，从系统可安全稳定运行的整体出发，对并网风电场的PI参数进行合理整定，以保证系统的小扰动稳定。

参考文献：

［1］WWEA.World wind energy report 2012［R］.Brussels，Belgium：World Wind Energy Association，2013.

［2］PENA R，CLARE JC，ASHER G M.Doublyfedinduction generatorusing back-to-back PWM converters and its application to variable-speed wind-energy generation［J］.IEE Proceedings of Electric Power Applications，1996，143（3）：231-241.

［3］薛禹胜，郝思鹏，刘俊勇，等.关于低频振荡分析方法的评述［J］.电力系统自动化，2009，33（3）：1-8.XUE Yusheng，HAO Sipeng，LIU Junyong，et al.A review of analysis methods for low-frequency oscillations［J］.Automation of Electric Power Systems，2009，33（3）：1-8.

［4］AKHMATOV V.Analysis of dynamic behavior of electric power systems with large amount of wind power［D］.Copenhagen，Denmark：Rsted DTU Technische，University of Denmark，2003.

［5］马静，高翔，李益楠，等.考虑风速随机特征的多工况电力系统稳定性分析［J］.电力自动化设备，2016，36（8）：26-32.MA Jing，GAO Xiang，LI Yinan，et al.Stability analysis considering time-varying wind speed for power system with multiple operating conditions［J］.Electric Power Automation Equipment，2016，36（8）：26-32.

［6］尹明，王成山，葛旭波，等.中德风电发展的比较与分析［J］.电工技术学报，2010，25（9）：157-162.YIN Ming，WANG Chengshan，GE Xubo，et al.Comparison and analysis of wind power development between China and Germany［J］.Transactions of China Electrotechnical Scoiety，2010，25（9）：157-162.

［7］高本锋，李忍，杨大业，等.双馈风电机组次同步振荡阻尼特性与抑制策略［J］.电力自动化设备，2015，35（12）：11-20.GAO Benfeng，LI Ren，YANG Daye，et al.Damping characteristic and countermeasure of DFIG sub-synchronous oscillation［J］.Electric Power Automation Equipment，2015，35（12）：11-20.

［8］KUNDUR P.Power system stability and control［M］.New York，USA：McGraw-Hill Inc，1994：669-817.

［9］谭谨，王晓茹，李龙源.含大规模风电的电力系统小扰动稳定研究综述［J］.电力系统保护与控制，2014，42（3）：15-23.TAN Jin，WANG Xiaoru，LI Longyuan.A survey on small signal stability analysis of power systems with wind power integration［J］.Power System Protection and Control，2014，42（3）：15-23.

［10］YATEENDRA M，MISHRA S，LI F X，et al.Small-signal stability analysis ofa DFIG-based wind powersystem under different modes of operation［J］.IEEE Transactions on Energy Conversion，2009，24（4）：972-982.

［11］LINASH P K，BIKASH C P，KEVIN J D.Electrical oscillations in wind farm systems：analysis and insight based on detailed modeling［J］.IEEE Transactions on Sustainable Energy，2016，7（1）：51-62.

［12］MIAO Z X，FAN L L，DALE O，et al.Control of DFIG-based wind generation to improve interarea oscillation damping［J］.IEEE Transactions on Energy Conversion，2009，24（2）：415-422.

［13］BABAK B，MANDHIR S S，ZHOU Y，et al.General methodology foranalysisofsub-synchronous interaction in wind power plants［J］.IEEE Transactions on Power Systems，2013，28（2）：1858-1869.

［14］GAUTAM D，VITTAL V，HARBOUR T.Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems［J］.IEEE Transactions on Power Systems，2009，24（3）：1426-1434.

［15］VITTAL E，O’MALLEY M，KEANE A.Rotor angle stability with high penetrations of wind generation［J］.IEEE Transactions on Power Systems，2012，27（1）：353-362.

［16］余贻鑫.电力系统安全域方法研究述评［J］.天津大学学报，2008，41（6）：635-646.YU Yixin.Review of study on methodology of security regions of power system［J］.Journal of Tianjin University，2008，41（6）：635-646.

［17］贾宏杰.电力系统小扰动稳定域的研究［D］.天津：天津大学，2001.JIA Hongjie.Studies on small signal stability region of power systems［D］.Tianjin：Tianjin University，2001.

［18］KWATNY H G，FISCHL R F，NWANKPA C O.Local bifurcation in power systems：theory，computation，and application ［J］.Proceedings of the IEEE，1995，83（11）：1456-1483.

［19］PARNIANI M，IRAVANI M R.Computer analysis of small-signal stability of power systems including network dynamics［J］.IEE Proceedings on Generation，Transmission and Distribution，1995，142（6）：613-617.

［20］孙强.电力系统小扰动稳定域及低频振荡［D］.天津：天津大学，2007.SUN Qiang.Power system small signal stability region and low-frequency oscillations［D］.Tianjin：Tianjin University，2007.

［21］VENKATASUBRAMANIAN V，SCHATTLER H，ZABORSZKY J.Dynamics of large constrained nonlinear systems-a taxonomy theory［J］.Proceedings of the IEEE，1995，83（11）：1530-1561.

［22］QIN Chao，YU Yixin.Small signal stability region of power systems with DFIG in injection space［J］.Journal of Modern Power Systems and Clean Energy，2013，1（2）：127-133.

［23］LIU Wenying，GE Rundong，LI Huiyong，et al.Impact of largescale wind power integration on small signal stability based on stability region boundary［J］.Sustainability，2014，6：7921-7944.