高压直流输电系统阻尼型双调谐交流滤波器的优化设计

辛清明，黄 莹，邱 伟，赵晓斌，李凌飞，卢毓欣

（南方电网科学研究院有限责任公司 直流输电技术国家重点实验室，广东 广州 510080）

0 引言

直流输电系统因其良好的经济性被广泛地应用于现代电力系统中。交流滤波器是直流输电系统中非常重要的设备，它既能滤除换流站产生的谐波电流，保证电能质量，同时也能够为换流站提供其正常运行所必需的无功。交流滤波器的设计需综合考虑经济技术因素，既取决于滤波的性能要求，也与系统谐波阻抗、换流站的无功需求等相关［1］。

双调谐交流滤波器等效于2个并联的单调谐滤波器，可以同时滤除2个不同频率的谐波，非常适合直流工程换流站的谐波治理。同时，双调谐滤波器只有1个谐波回路的电容需承受全部的冲击电压，占地面积小，相较于2个并联的单调谐滤波器具有较大的经济优势。因此双调谐滤波器在直流工程中得到了广泛的应用［2-7］。为了降低双调谐滤波器的失谐灵敏度、提高高频的阻尼特性，降低部分设备定值，在传统双调谐滤波器的基础上引入了阻尼式双调谐滤波器的概念［8-11］。

目前，关于双调谐滤波器的设计已有很多论述。基本的设计思路是将双调谐滤波器等效于2个单调谐滤波器。而针对阻尼式双调谐滤波器的阻尼电阻设计，则多采用试算法。该种方法具有盲目性，为得到优化的阻尼电阻，需反复核算交流滤波器性能和定值，计算量巨大［11-15］。文献［11］从交流滤波器滤波性能及定值2个方面对不同的阻尼式交流滤波器进行了研究，同时给出了阻尼电阻的合理取值范围，其结果对实际工程具有一定的参考作用。但其给出的阻尼电阻仅是一个范围，具体设计时仍需采用试算法进行取值，不仅设计的工作量大，而且很难找到最优的阻尼电阻，从而增加了交流滤波器设备的投资。

本文从双调谐滤波器的阻频特性出发，分别推导了不同形式的阻尼式双调谐滤波器的统一表达式，进而推导出适用于双调谐滤波器的分流比表达式。根据分流比影响，分析了阻尼电阻对交流滤波器性能指标的影响，推导了阻尼电阻与电话谐波波形系数（THFF）之间的关系，为电话谐波波形系数指标的优化提供计算依据。根据不同阻尼电阻的形式讨论了其对设备定值的影响，并推导了其对交流滤波器不同设备定值的影响公式，进一步给出了阻尼电阻对交流滤波器设备造价的影响公式，为交流滤波器的定值优化提供计算依据。最后总结了阻尼电阻优化设计流程，该设计方法在满足滤波器性能要求的前提下，以最优设备造价为目标，可快速完成阻尼电阻的优化设计。

1 阻尼式双调谐交流滤波器阻频特性

常见的阻尼式交流滤波器通用结构如图1所示，根据文献［11］，阻尼电阻可选择性地安装在R1、R2、R33个位置，R1为通常选择的位置。其中R1的主要作用是提高交流滤波器的高频特性，降低电话谐波波形系数的性能指标；R2的主要作用是降低低压谐振回路的定值；R3具有兼顾R1和R2两方面的作用。

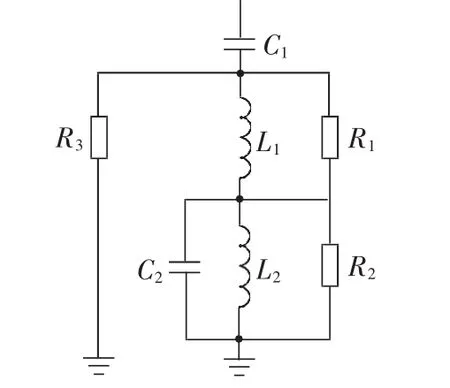
图1 阻尼式双调谐交流滤波器通用结构Fig.1 General structure of damping type double tuned AC filter

以R3为例，双调谐交流滤波器的h次谐波阻抗为：

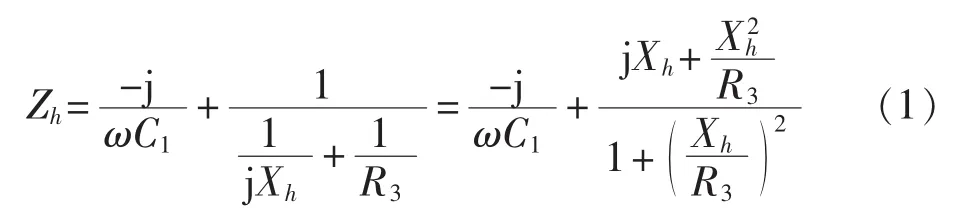
其中，为与R3并联部分的电抗。

令阻尼电阻比为 Xh/R3＝λh，则有：

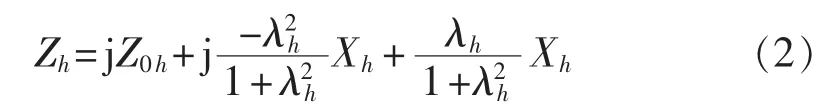
其中，为无阻尼双调谐交流滤波器h次谐波阻抗；λh为h次阻尼电阻比。同理，上述表达式可以作为R1、R2的滤波器阻抗统一表达式，其中：

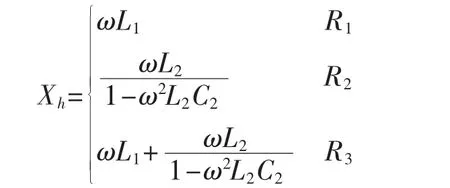
由上述表达式可知，R3的作用为R1和R2作用的综合。图2为阻尼电阻在不同位置时的滤波器阻频特性曲线。阻尼电阻均取500 Ω。

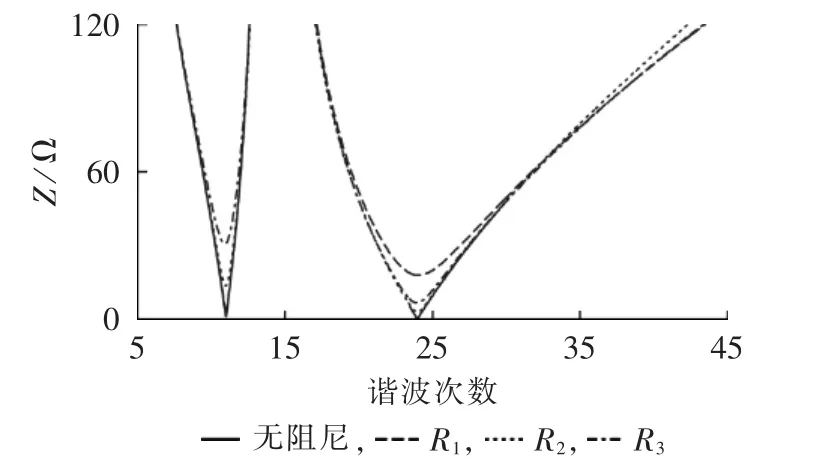
图2 不同阻尼电阻的双调谐交流滤波器阻频特性曲线Fig.2 Impedance-frequency characteristic curves of double tuned AC filter with different damping resistances

由图2可见，R1、R2和R3的引入主要改变了调谐点附近以及高频部分的阻频特性。其中R1、R2和R3的引入均可以使调谐点处的阻抗不同程度地增大；而在高频部分，R1和R3的引入将降低滤波器的高频阻抗，而R2的引入则对高频阻抗无影响。

交流滤波器的设计需先满足滤波器性能指标要求，然后计算设备定值，在满足性能要求的前提下，适当地优化设备定值。双调谐交流滤波器的调谐频率通常根据换流站的特征次谐波次数确定。进而通过调节滤波器电容、电抗的参数来使得单次谐波电压畸变率和总谐波电压畸变率满足限值要求。阻尼电阻的主要作用包括对滤波器的谐波阻抗进行微调，从而满足电话谐波波形系数的限值要求。同时阻尼电阻能够降低与之并联的设备定值，从而降低设备投入。

因此在双调谐滤波器中引入阻尼电阻主要考虑三方面的原则：不能过于改变调谐点附近的阻抗特性，以防止影响特征次谐波的滤波特性；降低交流滤波器的高频阻抗，以降低电话谐波波形系数指标；降低与阻尼电阻并联部分设备的定值，提高交流滤波器配置的经济性。其中前2个原则评估阻尼电阻对交流滤波器性能的影响，第3个原则评估阻尼电阻对设备定值的影响。

2 阻尼电阻对交流滤波器性能的影响分析

交流滤波器的性能指标包括［11］：单次谐波电压畸变率Dn，对于500 kV交流系统，奇次谐波电压畸变率典型限值为1%，偶次谐波电压畸变率典型限值为0.5%；总谐波电压畸变率Deff，通常Deff限值要求为1%~4%；电话谐波波形系数KTHFF，KTHFF的典型限值为1%，根据不同地区的情况，该限值可适当增大，尤其是在光纤通信地区。

性能计算用于考核不同工况下换流器产生的谐波的滤除效果，不考虑系统外部影响即忽略系统母线背景谐波的影响，计算模型如图3所示［1］。图中，Ih为换流站产生的h次谐波电流；Zfh为交流滤波器h次阻抗；Zsh为交流系统h次等效阻抗；Ifh和Ish分别为流入交流滤波器和交流系统的h次谐波电流；Uh为交流母线h次谐波电压。

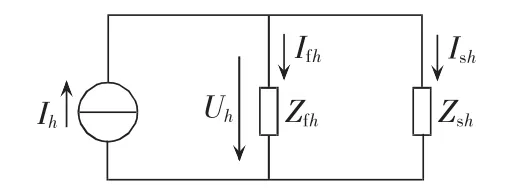
图3 交流滤波器性能计算原理图Fig.3 Schematic diagram of AC filter performance calculation

根据交流系统的实际状态，通常可假设系统阻抗为：

其中，Zsh与交流系统的短路容量相关。交流滤波器通常与交流系统阻抗组成并联关系，若流入交流滤波器的电流为Ifh，谐波电流源的电流为Ih，则可假设：

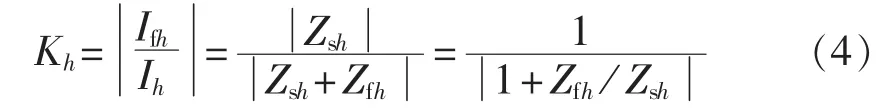
其中，Kh为滤波器支路对换流站母线谐波电流的分流比［7］。若选取交流系统等效阻抗为基准，则式（4）可表示为：

其中，上标*表示标幺值。根据式（2），Zfh可表示为：

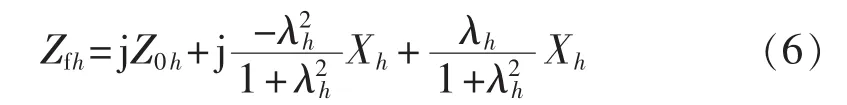
通常情况下，交流系统的阻抗角较大，可忽略交流系统等值电阻，则有：

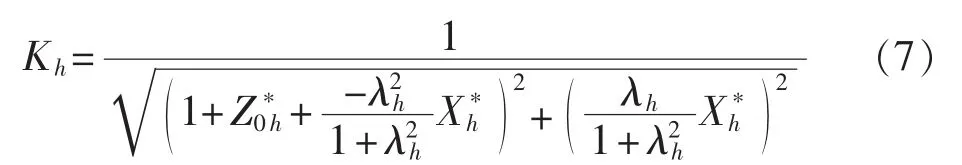
在滤波器设计中，通常要根据已有的系统条件，按照无阻尼双调谐滤波器先进行设计，因此式（7）中的和均为已知量，由此可以得到不同的阻尼电阻比与电流分流比之间的关系。

双调谐滤波器最为重要的是在调谐频率处的电流分流比，当频率为调谐频率时，Z0h=0，则分流比表达式可以简化为：

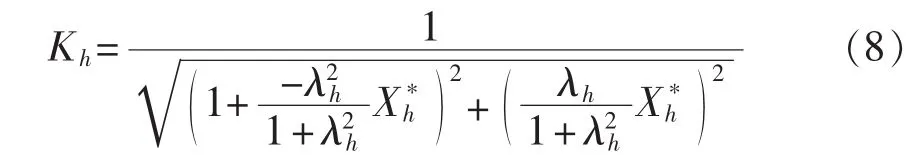
根据式（8）可以得到在可以接受的调谐点处的电流分流比的最小电阻，即确定阻尼电阻的最小值。

本文以直流工程中常用的双调谐滤波器DT11/24为例（双调谐滤波器通常用DT表示，11和24为该滤波器的调谐次数），滤波器的参数为：C1=2.298 μF，L1=12.649 mH，C2=5.407 μF，L2=9.422 mH，交流系统基频阻抗为20 Ω。则阻尼电阻与谐波分流比的关系如图4所示。

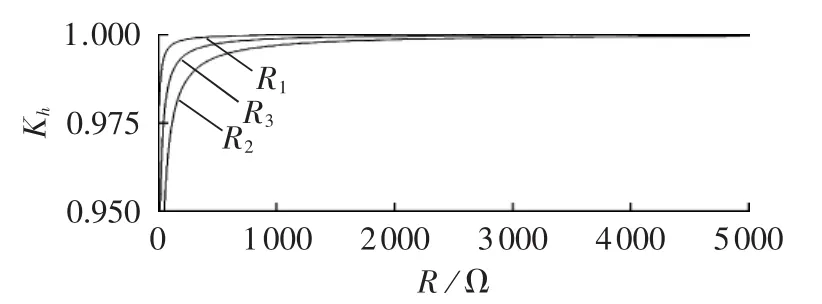
图4 不同阻尼电阻与谐波电流分流比的关系曲线Fig.4 Curve of harmonic current split ratio vs.damping resistance

由图4可见，R1对交流滤波器分流比的影响最小，R3次之，R2最大。阻尼电阻的具体取值与分流比的大小直接相关，但为了交流滤波器在调谐点处取得良好的滤波效果，通常R1不宜小于500 Ω，R2不宜小于 1500 Ω，R3不宜小于 2000 Ω。

早期的电话系统基于明线通信，目前电话通信系统已有重大改进，重要线路改用光纤通信，但明线通信仍占有重要地位。明线通信易受临近电力或通信线路中的音频电流干扰而降低信噪比，影响通话质量。因此，在涉及谐波问题的规范和设计时，电话干扰问题都是考虑的重点。电话谐波波形系数是基于换流站母线谐波电压水平的一种衡量电话干扰水平的指标。该指标符合IEC规定，在欧洲广泛使用，我国通常也采用该指标。

电话谐波波形系数公式为［1］：

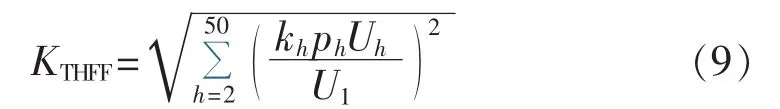
其中，kh=50h /800；ph=CCITT/1000，CCITT为噪声加权系数。文献［6］中给出了khph与频率的关系曲线，其值随频率的增大而增大。

根据直流工程换流站谐波电流理论，其特征次谐波往往要比非特征次谐波大1～2个数量级，因此在滤波时主要考虑特征次谐波。而根据设计经验，通常50次以上特征次谐波电流较小，可以忽略。在50 次以内的特征次谐波中，11 /13、23 /25、35 /37次谐波均可以通过DT11/24和DT13/36的配置进行滤除，因此影响电话谐波波形系数的主要特征次谐波为47、49次谐波。所以，在考虑降低电话谐波波形系数时，主要考虑R1和R3的作用，R2对于该指标的降低没有作用。

根据上述分析，阻尼电阻的加入主要对47次和49次谐波的影响较大，对其他次谐波特性的影响不大，可忽略其变化。根据滤波器阻抗特性，在高频时，其阻抗以及相角变化不大，可以通过48次来综合考虑47次、49次谐波电流的影响。为简化计算，可以采用下式对电话谐波波形系数指标进行考核。

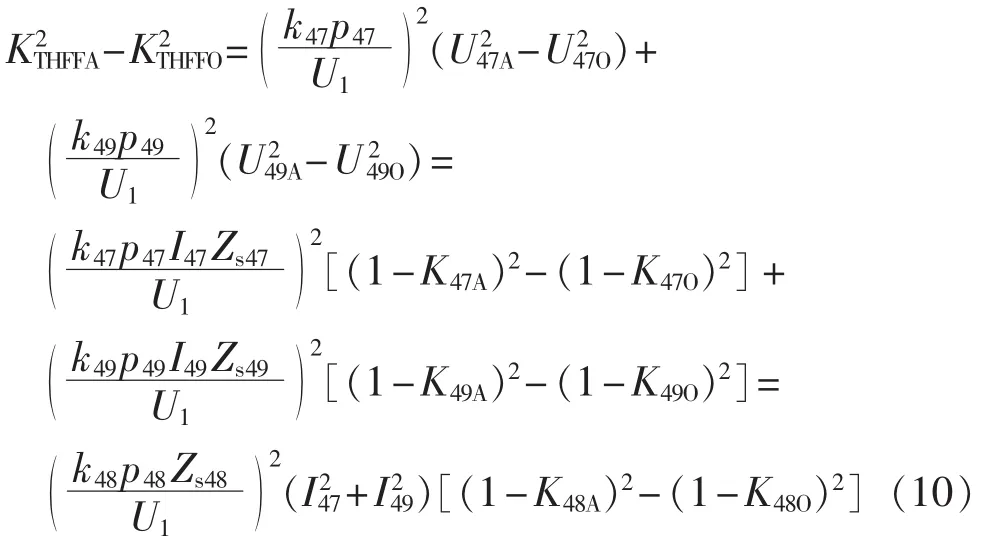
其中，KTHFFA为原电话谐波波形系数（不加并联电阻）；KTHFFO为目标电话谐波波形系数，通常可设定为电话谐波波形系数的限值；UhA、UhO分别为h次谐波电压的原值和目标值；KhA、KhO分别为h次谐波电流分流比的原值和目标值；Ih为换流变网侧h次谐波电流，h=47，49。

式（10）求出的电阻值为达到目标电话谐波波形系数的最大电阻值，当电阻值低于上述值时，一定能够满足电话谐波波形系数的要求。

仍以上述滤波器参数为例，图5为电话谐波波形系数与不同的并联阻尼电阻的关系曲线。由图5中的实线可见，R2对KTHFF的影响很小，尤其是当电阻较大时，几乎没有影响；而R1和R3的影响则较大。同时，存在一个合适的阻尼电阻，使KTHFF达到最小值，当电阻值低于该值时，反而会使KTHFF增大，这主要是因为电阻过小时，改变了滤波器在调谐点附近的阻抗特性，影响了滤波器对40次以下谐波的滤波效果，从而增大了KTHFF。

从图5中实线与虚线的对比来看，在大电阻区域，二者吻合得较好；在小电阻区域，二者差距较大，这主要是因为本文算法忽略了40次以下谐波对电话谐波波形系数的影响。因此本文算法在阻尼电阻不影响滤波器调谐点阻频特性的前提下，即阻尼电阻大于式（8）的最小阻尼电阻时，式（10）可以用于评估阻尼电阻对电话谐波波形系数的影响，并可以得到满足KTHFF限值要求的最大电阻值。

通过式（8）和式（10），可以确定使双调谐滤波器满足性能要求的阻尼电阻的取值范围，同时也可以确定使电话谐波波形系数最小的阻尼电阻取值。但阻尼电阻的具体取值还需要根据定值结果进行优化。

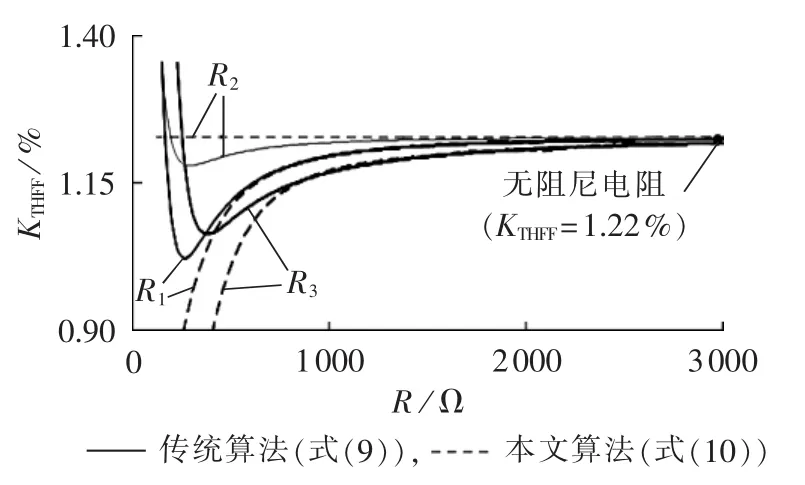
图5 不同阻尼电阻与电话谐波波形系数的关系曲线Fig.5 Curve of THFF vs.damping resistance

3 阻尼式双调谐滤波器的定值特性分析

阻尼电阻改变与之并联的设备定值主要是通过并联分流实现的，因此，R1只对L1有影响，R2只对L2以及 C2有影响，R3则对 L1、L2、C2均有影响。

仍以R3为例，有：

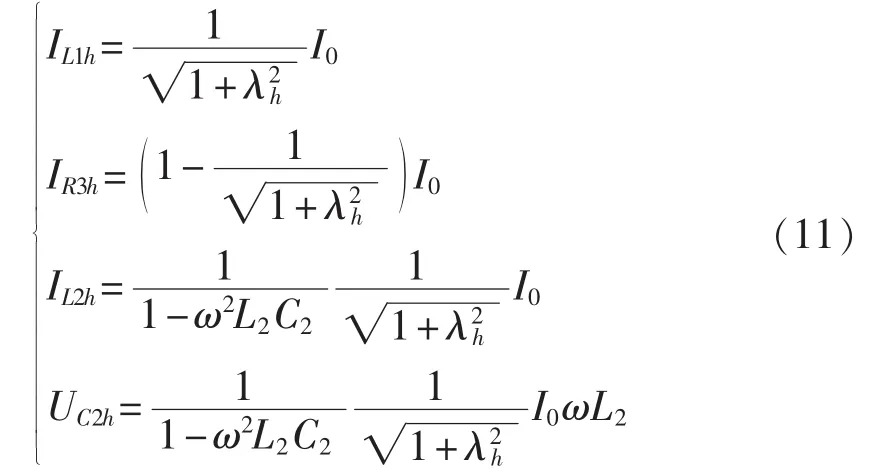
若无电阻并联，则L1上的谐波电流为I0，R3上的谐波电流为0，L2上的谐波电流为。

由式（11）可知，R3的并联对于L1的电流有减小作用，减小的程度取决于R3的大小，R3越小，L1电流越小。同样地，L2的电流也减小，其减小的程度与L1相同。对于C2上的电容电压，其变化趋势与L2的电流相同。

根据上述分析，R3的引入能够有效降低L1、L2以及C2的定值，但同时增加了R3的定值，所以需要综合评估并联阻尼电阻的引入对设备造价的影响。在评估设备造价时，可采用下式进行评估：

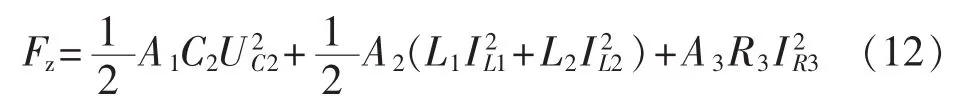
其中，UC2、IL1、IL2、IR3分别为各设备的总电压和电流定值；A1、A2、A3分别为电容器、电抗器、电阻器单位容量造价，其取值主要取决于各设备的造价，而设备造价是由多种因素决定的，且会随着市场变化进行调整。在市场稳定的情况下，对于同一电压等级的工程，各设备的单位容量造价可视为一个常数，可根据工程经验参数进行选取。由于并联阻尼电阻的引入对C1的设备定值没有影响，因此式（22）中没有列出该项。值得说明的是，式（12）只能粗略地预估设备的造价，但在一定范围内可以用于设备造价计算的指导，并可以指导设备的最优化设计。

式（12）对R1和R2同样适用。仍以上述DT11/24交流滤波器参数为例，图6为不同电阻选值与设备造价的关系曲线。

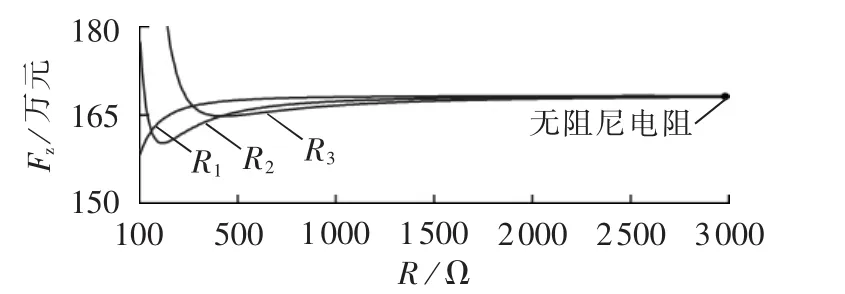
图6 不同阻尼电阻与设备造价的关系曲线Fig.6 Curve of equipment cost vs.damping resistance

由图6可见，随着电阻减小，设备造价逐渐降低，但当电阻小到一定程度时，设备造价反而上升，这主要是由于电阻器电流定值过大，导致电阻器成本升高，从而提高了设备总成本。因此，随着阻尼电阻的变化，设备造价存在一个最小值，可据此来优化阻尼电阻取值。

图6中各个设备的单位容量造价是根据实际工程经验选取的。单位容量造价的取值将会影响图6曲线的趋势，如当电阻器单位容量造价远远小于电容器（电抗器）单位容量造价时，电容器越小，总设备造价越低；当电阻器单位容量造价与电容器（电抗器）单位容量造价相当时，阻尼电阻的大小对设备造价几乎没有影响。无论单位容量造价取值如何，根据式（12），均能够找到一个使设备造价最低的最优电阻值。

图7（a）为双调谐交流滤波器阻尼电阻的传统设计流程。传统的阻尼电阻设计流程依靠工程经验，当初定的阻尼电阻选取不合理时，需要经过多次的反复核算，工作量大，且最终确定的阻尼电阻只能保证满足性能限值要求，无法保证设备造价的最优。图7（b）为本文提出的优化设计流程，通过式（8）和式（10）确定满足交流谐滤波器性能要求的阻尼电阻的取值区间，通过式（12）在上述取值区间内选取使设备造价最低的最优阻尼电阻值，得到的阻尼电阻既能满足交流滤波器限值要求，又可以降低设备定值，从而降低设备造价。

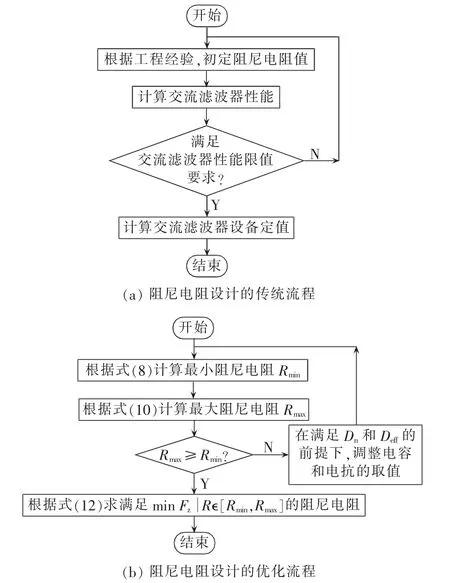
图7 阻尼电阻设计流程Fig.7 Flowchart of damping resistor design

4 结论

本文推导了不同形式阻尼式双调谐滤波器的统一阻频特性表达式，给出了双调谐滤波器的分流比表达式，并据此分析了阻尼电阻对交流滤波器性能和定值的影响。得到的主要结论如下。

a.不同位置阻尼电阻的引入使双调谐交流滤波器调谐点处的阻抗不同程度地增大，R1和R3的引入将降低滤波器的高频阻抗，而R2的引入则对高频阻抗无影响。

b.阻尼电阻越小，其对交流滤波器调谐点处的分流比影响越大。根据分流比表达式，可得到不影响交流滤波器调谐点的最小阻尼电阻。

c.R2对KTHFF的影响很小，尤其是当电阻较大时，几乎没有影响；而R1和R3的影响则较大。同时，存在一个合适的阻尼电阻，使KTHFF达到最小值。

d.随着电阻减小，设备造价逐渐降低，但当电阻小到一定程度，设备造价反而上升。

本文提出的阻尼电阻优化设计算法和流程，解决了阻尼式双调谐滤波器的阻尼电阻优化设计问题，避免了传统试算法的盲目性和巨大的工作量，并可以提高交流滤波器设备的经济性。

参考文献：

［1］赵畹君.高压直流输电工程技术［M］.北京：中国电力出版社，2004：193-196.

［2］李普明，徐政，黄莹，等.高压直流输电交流滤波器参数的计算［J］.中国电机工程学报，2008，28（16）：115-121.LI Puming，XU Zheng，HUANG Ying，et al.Algorithm for the parameters of AC filters in HVDC transmission system［J］.Proceedings of the CSEE，2008，28（16）：115-121.

［3］罗隆福，俞华，刘福生，等.高压直流输电系统中双调谐滤波器参数研究及其仿真［J］.电力自动化设备，2006，26（10）：25-27.LUO Longfu，YU Hua，LIU Fusheng，et al.Study on parameters of double tuned filter in HVDC transmission system and its simulation［J］.Electric Power Automation Equipment，2006，26（10）：25-27.

［4］康明才，黄锦安，陈建业，等.高压直流输电系统双调谐滤波器元件参数分析［J］.华北电力大学学报，2010，32（增刊 1）：91-93.

［5］毛涛，乐健，黄银龙，等.参数失谐对基于滤波器的高压直流输电系统直流侧谐波电压测量的影响［J］.电力自动化设备，2015，35（12）：95-100.MAO Tao，LE Jian，HUANG Yinlong，et al.Influence of parameter mismatch on filter-based harmonic voltage measuring for DC side of HVDC transmission system［J］.Electric Power Automation Equipment，2015，35（12）：95-100.

［6］苏炜.直流输电换流站交流滤波器研究［D］.北京：华北电力大学，2004.SU Wei.Research on AC filter for HVDC converter station［D］.Beijing：North China Electric Power University，2004.

［7］杜习周，蒋建东，李强，等.灵宝换流站交流滤波器滤波效果分析［J］.西南大学学报（自然科学版），2016，38（1）：1-5.DU Xizhou，JIANG Jiandong，LI Qiang，et al.An analysis of the filtering effect of the AC filter in Lingbao converter station［J］.Journal of Southwest University（Natural Science），2016，38（1）：1-5.

［8］薛英林，李普明，徐政，等.同塔双回高压直流工程交流滤波器设计［J］.电力系统自动化，2010，34（17）：50-54.XUE Yinglin，LI Puming，XU Zheng，et al.Design of alternating current filter for double circuit high voltage direct current transmission project［J］.Automation of Electric Power Systems，2010，34（17）：50-54.

［9］倪常茂，刘振兴.基于双调谐滤波器和TSC的混合型无功补偿滤波装置［J］.电力自动化设备，2012，32（7）：124-128.NI Changmao，LIU Zhenxing.Hybrid reactive power compensation and filtering device based on dual tuning filter and TSC ［J］.Electric Power Automation Equipment，2012，32（7）：124-128.

［10］朱光友.换流站交流侧谐波电流计算与交流滤波器设计研究［D］.杭州：浙江大学，2007.ZHU Guangyou.Calculation of AC side harmonic current and design of AC filter at convertor station［D］.Hangzhou：Zhejiang University，2007.

［11］薛英林，徐政，李普明，等.高压直流输电双调谐滤波器阻尼电阻的选取原则［J］.电力系统自动化，2011，35（13）：92-97.XUE Yinglin，XU Zheng，LI Puming，et al.Selection principle of damping resistor for double-tuned filter in HVDC system［J］.Automation of Electric Power Systems，2011，35（13）：92-97.

［12］同向前，薛均义.电力调谐滤波器的最佳偏调谐设计［J］.电工技术学报，2005，20（4）：98-101.TONG Xiangqian，XUE Junyi.Tuned power filter with optimal tuned frequency［J］.Transactions of China Electrotechnical Society，2005，20（4）：98-101.

［13］黄莹，黎小林，饶宏，等.云广±800 kV直流输电工程交流滤波器设计关键问题研究［J］.南方电网技术，2010，4（2）：67-71.HUANG Ying，LI Xiaolin，RAO Hong，et al.Study on the key issues of AC filter design for Yunnan-Guangdong±800 kV DC project［J］.Southern Power System Technology，2010，4（2）：67-71.

［14］苏炜，马为民.直流输电换流站交流滤波器稳态额定值研究［J］.高电压技术，2004，30（11）：63-64.SU Wei，MA Weimin.AC filter steady state rating in HVDC converter station［J］.High Voltage Engineering，2014，30（11）：63-64.

［15］肖遥.三调谐滤波器的参数计算方法［J］.南方电网技术，2005，1（3）：43-46.XIAO Yao.Algorithm for the parameters of triple tuned filter［J］.Southern Power System Technology，2005，1（3）：43-46.